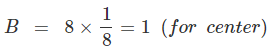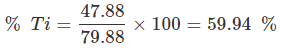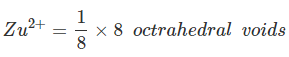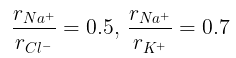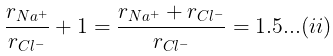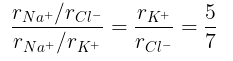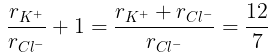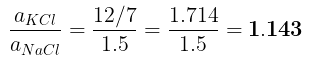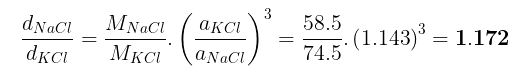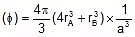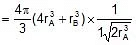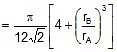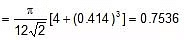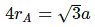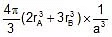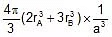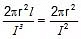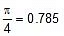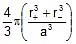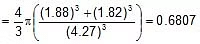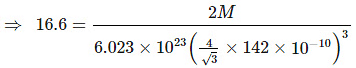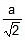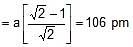Solved Examples: The Solid State | Chemistry for JEE Main & Advanced PDF Download
Example 1. Select right statement(s):
(a) 8 Cs ions occupy the second nearest neighbour locations of a Cs ion.
(b) Each sphere is surrounded by six voids in a two-dimensional hexagonal close-packed layer.
(c) If the radius of cations and anions are 0.3 Å and 0.4 Å then a coordinate the number of cation of the crystal is 6.
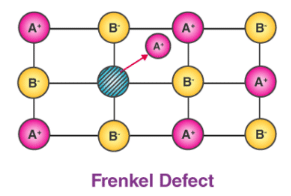
(d) In AgCl, the silver ion is displaced from its lattice position to an interstitial position such a defect is called a Frenkel defect.
Correct Answer is Option (d)
(a) 6 Cs ion second nearest neighbour(b)
(c) r+\r- = 0.75 (BCC) 8 : cordination no.
(d)
Example 2. Which of the following statement is/are incorrect in the rock-salt structure of an ionic compound?
(a) The coordination number of cation is four whereas that of anion is six.
(b) The coordination number of cation is six whereas that of anion is four.
(c) The coordination number of each cation and anion is four.
(d) The coordination number of each cation and anion is six.
Correct Answer is Option (d)
Coordination no. of cation = 6
Coordination no. of anion = 6
Example 3. Which of the following statements are correct?
(a) The coordination number of each type of ion in CsCl is 8.
(b) A metal that crystallizes in BCC structure has a coordination number 12.
(c) A unit cell of an ionic crystal shares some of its ions with other unit cells.
(d) The length of the unit cell in NaCl is 552 pm.
Correct Answer is Option (d)
r+ + r- = a/2 ⇒ (95 + 181) = a/2
⇒ a = 276 × 2 = 552 pm
Example 4. A cubic solid is made up of two elements A and B. Atoms B are at the corners of the cube and A at the body centre. What is the formula of the compound?
A = 1 (Body center),
Formula = AB
Example 5. A compound alloy of gold and copper crystallizes in a cubic lattice in which gold occupies that lattice point at corners of the cube and copper atom occupy the centres of each of the cube faces. What is the formula of this compound?
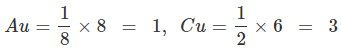
Formula = AuCu3
Example 6. A cubic solid is made by atoms A forming a close pack arrangement, B occupying one. Fourth of tetrahedral void and C occupying half of the octahedral voids. What is the formula of the compound?
A =
= 4
B =
no. of void (tetrahedral) = 2
C = Total no. of octahedral voids = 2
No. of octahedral voids (effective)= 1 12 × 1/4 = 4
Bodycenter/edgecentre = 4/2 = 2
formula = A4B2C2
Example 7. What is the percent by mass of titanium in rutile, a mineral that contains Titanium and oxygen, if the structure can be described as a closet packed array of oxide ions, with titanium in one-half of the octahedral holes? What is the oxidation number of titanium?
O2- =
+
× 6 = 4, Ti =
Formula:
TiO2 ⇒ Ti (At mass) = 47.88
Ox. State = 4
Example 8. Spinel is an important class of oxides consisting of two types of metal ions with the oxide ions arranged in a CCP pattern. The normal spinel has one-eight of the tetrahedral holes occupied by one type of metal ion and one half of the octahedral hole occupied by another type of metal ion. Such a spinel is formed by Zn2+, Al3+ and O2-, with Zn2+ in the tetrahedral holes. Give the formulae of spinel.
Zn2+ = 8/8 = 1, Al3+ = 4/2 = 2, O2- = CCP (4)
ZnAl2O4:
O2- = CCP arrangment (1 3) = 4
Example 9. Iron occurs as bcc as well as fcc unit cell. If the effective radius of an atom of iron is 124 pm. Compute the density of iron in both these structures.
In BCC, Z = 2,
, r =
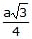
⇒ a =in pm
⇒ ρ = 7.92 × 106 g/cm3
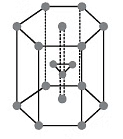
In FCC , Z = 4,
= 8.6 g/cm3
Example 10. A closed packed structure of uniform spheres has an edge length of 534 pm. Calculate the radius of the sphere, if it exists in
(a) Simple Cubic Lattice
(b) BCC lattice
(c) FCC lattice
(a) 2r = a ⇒ r =
=
= 267 pm
(b) 4r =
⇒ r =
= 231.23 pm
(c) 4r =
⇒ r =
= 188.79 pm
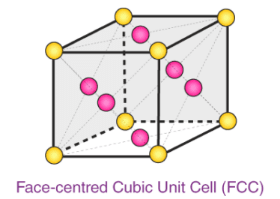
Example 11. Calculate the density of diamond from the fact that it has face centered cubic structure with two atoms per lattice point and unit cell edge length of 3.569 Å.
In simple FCC, Z = 4, but here from questions two atoms per lattice point.
⇒ Z = 8
⇒=
= 3.5 × 106 g/m3 = 3.5 g/cm3
Example 12. An element crystallizes into a structure which may be described by a cubic type of unit cell having one atom on each corner of the cube and two atoms on one of its body diagonals. If the volume of this unit cell is 24 × 10-24 cm3 and the density of the element is 7.2 g cm-3, calculate the number of atoms present in 200 g of the element.
Z = 3
7.2 =
⇒ M = 34.68
No. of atoms in 200 gram =
× 6.022 × 1023 = 3.47 × 1024 atoms
Example 13. Silver has an atomic radius of 144 pm and the density of silver is 10.6 g cm-3. To which type of cubic crystal, silver belongs?
ρ = 10.6 × 106 g/m3 =
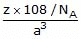
⇒P.F. =
=
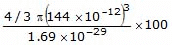
⇒ P.F. = 74 %
⇒ Crystal structure for silver is F.C.C.
Example 14. AgCl has the same structure as of NaCl. The edge length of a unit cell of AgCl is found to be 555 pm and the density of AgCl is 5.561 g cm-3. Find the percentage of sites that are unoccupied.
If 100% sites occupied = 5.575, but density is 5.561
⇒ % sites occupied =
∴ % sites unoccupied = 100 - (99.75) % = 0.25%
Example 15. Xenon crystallizes in the face-centred cubic lattice and the edge of the unit cell is 620 pm. What is the nearest neighbour distance and what is the radius of the xenon atom?
Nearest neighbour distance = 2r (in FCC)
⇒
= 4r
⇒ 2r =
=
= 438.47
r = 219.23
Example 16. The two ions A and B- have radii 88 and 200 pm respectively. In the closed packed crystal of compound AB, predict the coordination number of A.
(r+\r-) = 0.44
It could be a square planer or octahedral void but for the closed packed crystal it is an octahedral void.
Its coordination no. = 6
Example 17. CsCl has the bcc arrangement and its unit cell edge length is 400 pm. Calculate the interionic distance in CsCl.
Interionic distance, r + r- =
=
= 346.4 pm
Example 18. Gold crystallizes in a face-centred cubic lattice. If the length of the edge of the unit cell is 407 pm, calculate the density of the gold as well as its atomic radius assuming it to be spherical. The atomic mass of gold = 197 amu.
FCC : Z = 4
= 19.41 × 106 g/m3 = 19.41 g/cm3
2r =
⇒
Example 19. The density of KBr is 2.75 g cm-3. The length of the edge of the unit cell is 654 pm. Show that KBr has a face-centred cubic structure.
(N = 6.023 × 1023 mol-1, At. mass : K = 39, Br = 80)
⇒
= 7.18 × 10-23
Z = (654 × 10-10)3 / (7.18 × 10-23) = 4⇒ Crystal structure is FCC
Example 20. An element crystallizes in a structure having an FCC unit cell of an edge 200 pm. Calculate the density, if 200 g of this element contains 24 × 1023 atoms.
24 × 1023 atoms are contained by 200 g
6 × 1023 atoms are contained by= 50 g
M = 50 g/mole
=
=
=
ρ = 41.67 g/cm3
Example 21. The effective radius of the iron atom is 1.42 Å. If has FCC structure. Calculate its density
(Fe = 56 amu)
r =
⇒
⇒ a = 4.016 Å
= 0.574 × 107 g/m3 = 5.74 g/cm3
Example 22. A crystal of lead (II) sulphide has a NaCl structure. In this crystal, the shortest distance between Pb2 ion and S2- ion is 297 pm. What is the length of the edge of the unit cell in lead sulphide? Also, calculate the unit cell volume.
NaCl type FCC structure,
⇒ r+/r- == 297
⇒ a = 297 × 2 = 594 pm = 5.94 × 10-8 cm
a3 = volume % = 2.096 × 10-22 cm3
Example 23. If the length of the body diagonal for CsCl which crystallizes into a cubic structure with Cl- ions at the corners and Cs ions at the centre of the unit cells is 7 Å and the radius of the Cs ion is 1.69 Å, what is the radii of Cl- ion?
⇒ r+ + r- =
=
⇒ 1.69 + r- = 3.5
⇒ r- = 3.5 - 1.69 = 1.81 Å
Example 24. In a cubic closed packed structure of mixed oxides the lattice is made up of oxide ions, one-eighth of tetrahedral voids are occupied by divalent ions (A2) while one-half of the octahedral voids occupied trivalent ions (B3). What is the formula of the oxide?
Total tetrahedral voids = 8,
⇒ A2 occupied
Total octahedral void = 4,⇒ B3 occupied =
= 2
⇒ no. of atoms: A2 = 1, B3 = 2, O2- = 4∴ Formula = AB2O4
Example 25. A solid A and B- has a NaCl type closed packed structure. If the anion has a radius of 250 pm, what should be the ideal radius of the cation? Can a cation C having a radius of 180 pm be slipped into the tetrahedral site of the crystal of A B-? Give reasons for your answer.
for ideal NaCl crystal
⇒ r- =
r = 103.55 pm
tetrahedral sites for tetrahedral voids,0.225 <
< 0.414 ⇒
∴ No, a cation can't be slipped into a tetrahedral site of crystal
Example 26. If the radius of Mg2 ion, Cs ion, O2- ion, S2- ion and Cl- ion are 0.65 Å, 1.69 Å, 1.40 Å, 1.84 Å, and 1.81 Å respectively. Calculate the coordination numbers of the cations in the crystals of MgS, MgO and CsCl.
Example 27. In a cubic crystal of CsCl (density = 3.97 gm/cm3) the eight corners are occupied by Cl- ions with Cs ions at the centre. Calculate the distance between the neighbouring Cs and Cl- ions.
3.94 =
⇒
= 7.05 × 10-23 cm3
a = 4.13 × 10-8 cm
r+ + r- == 3.577 × 10-10 cm = 3.577 Å
Example 28. Calculate the value of Avogadro's number from the following data:
Density of NaCl = 2.165 cm-3
Distance between Na and Cl- in NaCl = 281 pm.
d =
⇒ 2.165 =
⇒ NA = 6 × 1023
Example 29. KCl crystallizes in the same type of lattice as does NaCl. Given that and Calculate:
(a) The ratio of the sides of unit cell for KCl to that for NaCl and
(b) The ratio of densities of NaCl to that for KCl
(a)
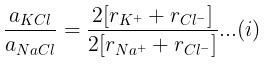
From eq. (i),
(b)
Example 30. An element A (Atomic weight = 100) having bcc structure has unit cell edge length 400 pm. Calculate the density of A and number of unit cells and number of atoms in 10 gm of A.
a = 400 pm = 4 × 10-8 cm, Z = 2
d ==
=
= 5.188 gm/cc
In 100 gm ⇒ 6.023 × 1023 atoms
In 10 gm ⇒ 6.023 × 1022 atoms
Example 31. The composition of a sample of wustite is Fe0.93 O1.0. What percentage of iron is present in the form of Fe(III)?
Fe : O = 93 : 100
Let Fe (III) = x, then Fe (II) = (93 - x)
Balancing charge, We have,
x × 3 (93 - x) × 2 = 100 × 2
x = 200 - 186 = 14
% Fe (III) = (14/93) × 100 = 15.05 %
Example 32. BaTiO3 crystallizes in the perovskite structure. This structure may be described as a cubic lattice with barium ions occupying the corner of the unit cell, oxide ions occupying the face-centres and titanium ion occupying the centre of the unit cell.
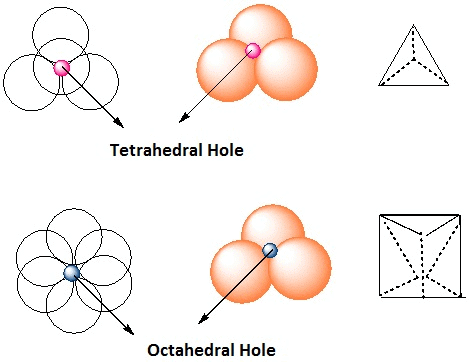
(a) If titanium is described as occupying holes in BaO lattice, what type of holes does it occupy?
(b) What fraction of this type of hole does it occupy?
(a) Ti is present at the body centre i.e. it occupies octahedral hole.
(b) No. of octahedral in c.c.p. = 4
- There is one Ti atom in each unit cell and there are four octahedral voids in each unit cell with each octahedral void contributing 1 atom to the unit cell.
- One-fourth of four octahedral voids contributes 1 Ti atom to the unit cell.
Example 33. Rbl crystallizes in BCC structure in which each Rb is surrounded by eight iodide ions each of radius 2.17 Å. Find the length of one side of the RbI unit cell.
= 0.732 Q
= 0.732 × 2.17 = 1.59 Å
a
= 2 [
] a =
[1.59 2.17] = 4.34 Å
Example 34. Find the size of the largest sphere that will fit in an octahedral void in an ideal FCC crystal as a function of atomic radius 'r'. The insertion of this sphere into the void does not distort the FCC lattice. Calculate the packing fraction of FCC lattice when all the octahedral voids are filled by this sphere.
If the Radius of the sphere is r, then the radius of the largest sphere that will fit in the octahedral void is 0.414 r.
2[r + 0.414 r] = a ⇒ 2.828 r = a
Volume of spheres = 4 × pr3 4 × p(0.414r)3 =pr3 [1 0.071]
Volume of unit cell = a3 = (2r)3 = 16
r3 , f =
=
= 0.793
⇒ 79.3%
Example 35. NaH crystallizes in the same structure as that of NaCl. The edge length of the cubic unit cell of NaH is 4.88 Å.
(a) Calculate the ionic radius of H-, provided the ionic radius of Na is 0.95 Å.
(b) Calculate the density of NaH.
a = 4.88 Å = 4.88 × 10-8 cm
(a)
=
,
= 2.44 - 0.95 = 1.49 Å
(b) d =
=
= 1.37 gm/cm3
Example 36. Metallic gold crystallizes in fcc lattice. The length of the cubic unit cell is a = 4.07 Å.
(a) What is the closest distance between gold atoms.
(b) How many "nearest neighbours" does each gold atom have at the distance calculated in (a).
(c) What is the density of gold?
(d) Prove that the packing fraction of gold is 0.74.
a = 4.07 Å
(a) 4r = a
⇒ r =
=
= 1.44 Å
Closest distance between An atoms = 2.88 Å
(b) C.N. = 12
(c) d ==
= 19.4 gm/cc
Example 37. Graphite is an example of:
(a) Ionic solid
(b) Covalent Solid
(c) Vander Waal's Crystal
(d) Metallic crystal
Correct Answer is Option (b)
Graphite is a covalent solid having sp2 hybridised carbon atoms.
Example 38. Which is amorphous solid:
(a) Rubber
(b) Plastic
(c) Glass
(d) All
Correct Answer is Option (d)
Amorphous solids neither have ordered arrangement (i.e. no definite shape) nor have a sharp melting point like crystals, but when heated, they become pliable until they assume the properties usually related to liquid. It is therefore they are regarded as supercooled liquids.
Example 39. Xenon crystallizes in face centre cubic lattice and the edge of the unit cell is 620 PM, then the radius of the Xenon atom is:
(a) 219.20 pm
(b) 438.5 pm
(c) 265.5 pm
(d) 536.94 pm
Correct Answer is Option (a)
For fcc lattice;
where, a = 620 pm
On solving, r = 219.20 pm
Example 40. The edge length of the cube is 400 PM. Its body diagonal would be:
(a) 500 pm
(b) 693 pm
(c) 600 pm
(d) 566 pm
Correct Answer is Option (b)
In body centre cubic,
body diagonal ==
pm = 692.82 pm ~ 693 pm
Example 41. What is the simplest formula of a solid whose cubic unit cell has atom A at each corner, the atom B at each face centre and a C atom at the body centre:
(a) AB2C
(b) A2BC
(c) AB3C
(d) ABC3
Correct Answer is Option (c)
- An atom at the corner of a cube is shared among 8 unit cells. As there are 8 corners in a cube, the number of corner atom (A) per unit cell = 8 ×
= 1.
- A face-centred atom in a cube is shared by two unit cells. As there are 6 faces in a cube, the number of face-centred atoms (B) per unit cell = 6 ×
= 3.
- An atom in the body of the cube is not shared by other cells. The number of atoms (C) at the body centre per unit cell = 1.
Hence, the formula of the solid is AB3C.
Example 42. A compound alloy of gold and copper crystallizes in a cube lattice in which the gold atoms occupy the corners of a cube and the copper atoms occupy the centres of each of the cube faces.The formula of this compound is-
(a) AuCu
(b) AuCu2
(c) AuCu3
(d) None
Correct Answer is Option (c)
One-eighth of each corner atom (Au) and one-half of each face-centred atom (Cu) are contained within the unit cell of the compound.
Thus, the number of Au atoms per unit cell = 8 ×
= 1 and the number of Cu atoms per unit cell = 6 × (1/2) = 3. The formula of the compound is AuCu3.
Example 43. Select the correct statement (s)-
(i) The C.N. of cation occupying a tetrahedral hole is 4.
(ii) The C.N. of cation occupying an octahedral hole is 6.
(iii) In Schottky defects, the density of the lattice decreases.
(a) i, ii
(b) ii, iii
(c) i, ii, iii
(d) i, iii
Correct Answer is Option (c)
Since tetrahedral holes are surrounded by 4 nearest neighbours. So, the C.N. of cation occupying tetrahedral hole is 4. Since octahedral hole is surrounded by six nearest neighbours. So, C.N. of cation occupying octahedral is 6. In schottky, a pair of anion and cation leaves the lattice. So, density of lattice decreases.
Example 44. Lithium borohydride (LiBH4), crystallises in an orthorhombic system with 4 molecules per unit cell. The unit cell dimensions are : a = 6.81 Å, b = 4.43 Å , c = 717 Å. If the molar mass of LiBH4 is 21.76 g mol-1 . The density of the crystal is:
(a) 0.668 g cm-3
(b) 0.585 g cm-3
(c) 1.23 g cm-3
(d) None
Correct Answer is Option (a)
We know that: ρ =; where V = a × b × c
⇒ ρ =
= 0.668 g cm-3
Example 45. The unit cell of a metallic element of atomic mass 108 and density 10.5 g/cm3 is a cube with an edge length of 409 PM. The structure of the crystal lattice is -
(a) FCC
(b) BCC
(c) HCP
(d) None of these
Correct Answer is Option (a)
Here, M = 108, NA = 6.023 x 1023, a = 409 PM = 4.09 x 10-8 cm
Put on these values and solving we get: ρ = 10.5 g/cm3
n = 4 = number of atoms per unit cell
Thus, The structure of the crystal lattice is FCC.
Example 46. Among the following types of voids, which one is the largest void-
(a) Triangular system
(b) Tetragonal system
(c) Monoclinic system
(d) Octahedral
Correct Answer is Option (d)
The vacant spaces between the spheres in a closed packed structure is called void. The voids are of two types, tetrahedral voids and octahedral voids. Also, the radius of tetrahedral voids and octahedral voids are rvoid = 0.225 × rsphere and rvoid = 0.411 × rsphere respectively.
Thus, the octahedral void is larger than the tetrahedral void.
Example 47. Close packing is maximum in the crystal which is:
(a) Simple cube
(b) BCC
(c) FCC
(d) None of these
Correct Answer is Option (c)
The close packing in the crystal is 0.52, 0.68 and 0.74 for simple cubic, bcc, and fcc respectively.
i.e the close packing is maximum is fcc.
Example 48. Bragg's equation is:
(a) nl = 2q sin q
(b) nl = 2d sinq
(c) 2nl = d sin q
(d) l = (2d/n) sin q
Correct Answer is Option (b)
Bragg's equation: nl = 2d sin q
Example 49. Copper metal has a face-centred cubic structure with the unit cell length equal to 0.361 nm. Picturing copper ions in contact along the face diagonal, The apparent radius of a copper ion is:
(a) 0.128
(b) 1.42
(c) 3.22
(d) 4.22
Correct Answer is Option (a)
For a face-centred cube, we have,
radius =
=
nm = 0.128.
Example 50. The rank of a cubic unit cell is 4. The type of cell as:
(a) Body centred
(b) Face centred
(c) Primitive
(d) None
Correct Answer is Option (b)
The number of atoms present in sc, fcc and bcc unit cells are 1, 4, 2 respectively.
Example 51. At room temperature, sodium crystallises in a body centred cubic cell with a = 4.24 Å. The theoretical density of sodium is: (Atomic mass of sodium = 23.0 g mol-1)
(a) 2.05 g cm-3
(b) 3.45 g cm-3
(c) 1.00 g cm-3
(d) 3.55 g cm-3
Correct Answer is Option (c)
The value of Z for a bcc unit cell is 2.
Volume V = (4.24 Å)3r =
=
= 1.00 g / cm-3
Example 52. A face-centered cubic solid of an element A has a largest sized guest atom B at the body centre octahedral hole if insertion of B doesn't affect the original unit cell dimension; determine the packing fraction of the solid.
Sol. In the given solid, there is one B and four A per unit cell.
Also, under the condition of largest possible size of B, it will be in contact of A present at the face centres only and the following relationship will exist:
and 2(rA + rB) = a
solving,Now, packing fraction
Example 53. An element A has BCC structure and another guest atom B, of largest possible size are present at each edge centres of unit cell of A but without disturbing the original unit cell dimension. Determining the void percentage of this solid.
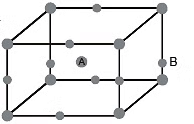
Sol. Since B is closer to corner than to face centre, in close contact,
2(rA + rB) = aIn a unit cell, there are two A and 12 × = 3BPacking fraction (f) =
⇒ Void space = 31.6%
Example 54. An element A has a BCC structure and another guest atoms B, of largest possible size, are present at the face centres, but without disturbing the unit cell dimension. Determine the packing fraction of this solid.
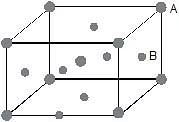
Sol. In the above solid, face centres are closer to body centre, therefore, the relationship.
2(rA rB) = 0⇒
Now, packing fraction (f) =
= 0.684
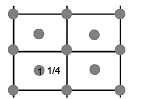
Example 55. Calcium has face-centred cubic lattice and radius of calcium atom is 195.6 picometre. Determine the number of Ca atoms present on surfaces of a mm3 block of calcium metal assuming that atoms in the closest packing calcium metal assuming that atoms are in the closest packing.
Sol. In FCC, the relation is
⇒
= 553.24 × 10-9 mm.
⇒ Area of a face of unit cell = a3 = 3.06 × 10-13 mm2
⇒ Surface area of metal block = 6 mm2
⇒ Total number of faces of unit cells present on surface
== 1.96 × 1013
Each face contributes two Ca atoms on surface as shown in diagram.
⇒ Total number of Ca atoms present on surface
= 2 × 1.96 × 1013 = 3.92 × 1013
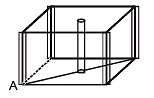
Example 56. An atom crystallizes in hexagonal closed packed arrangement. Determine dimensions (radius and length) of a large cylindrical atom that can be accommodated in the centre of HCP, in terms of radius of host atom.
Sol. The cylinder will pass through centre of middle layer and will lie between the face centres.
Therefore,
Height of cylinder (h) = height of hexagon (h) = 2r
Since, in HCP :,where r = radius of atoms.
r = 1.266 rAlso, if R is the radius of cylinder, then in the case of closet contact :
⇒ R = 0.155 r,⇒ h = 1.266 r
Example 57. A uniform cylindrical, polymer molecule crystallizes in body centred cubic array. Determine the packing fraction of this polymer in solid state assuming that molecules are in their closest contact.
Sol. The arrangement of molecules can be represented as follows :
Here,
⇒
Packing fraction (f) =
=
Example 58. Show the following arrays of atoms on a plane in an atomic FCC.
(A)
(B)
(C)
(D)
Sol.
(A)(B)
(C)
(D)
Example 59. Cesium bromide crystallizes in cubic arrangement like CsCl. Given the ionic radii of Cs and Br- are 1.88 Å and 1.82 Å respectively, determine the packing fraction.
Sol. Here Cs ion is at body centre and Br- at the corners, therefore the relationship is
2(r++ r-) =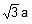
= 2 (1.88 1.82) Å,⇒ a = 4.27 Å
Packing fraction (f) =
Example 60. Titanium metal crystallizes in a BCC arrangement and radius of an atom is 142 picometre. Determine the atomic weight of titanium if the density is 16.6 g/cm3. Also determine the number of unit cells present in a 5 cm3 block of titanium metals.
Sol. In BCC arrangement of atoms, the relationship between edge length radius of the atom isDensity (r) =
Where, N = Number of atoms per unit cell,M = Molar mass, NA = Avogadro's number
V = Volume of unit cell
Here, the radius is taken in cm unit since, density is in g/cm3 unit.
Solving : M = 176. Also mass of 5 cm3 block = 5 × 16.6 = 83 g⇒ Number of atoms is 5 cm3 block⇒ Number of unit cells
=
= 1.42 × 1023
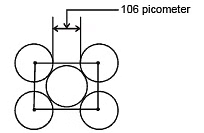
Example 61. Copper metal crystallizes in face-centered cubic arrangement and surface of adjacent atoms along the edge of the unit cell are 106 picometres apart. Determine the density of metal. Atomic mass of copper metal is 63.5 u.
Sol. According to the given information, a view of one face of the unit cell will be as shown below.
In FCC; 4√2a
The given distance is a - 2r = a -
⇒ a = 362 pm = 3.62 × 10-8 cm
= 8.89 g/cm3
Example 62. Potassium crystallizes in "body centered cubic" arrangement and the surfaces of the adjacent atoms along the edges of unit cells are 71.4 picometre apart. Determine the density of metal. Atomic weight of K = 39. ?
Sol. In BCC, the relationship between edge length and radius of atom is
Also, given a - 2r = 71.4 × 10-10 cm
⇒⇒ 71.4 × 10-10 cm
⇒ a = 5.329 × 10-10 cm= 0.855 g/cm3
|
361 videos|822 docs|301 tests
|
FAQs on Solved Examples: The Solid State - Chemistry for JEE Main & Advanced
| 1. What is the difference between crystalline and amorphous solids? |  |
| 2. How does the structure of a solid affect its properties? |  |
| 3. Can you explain the concept of unit cells in solid-state chemistry? |  |
| 4. What are the various types of bonding present in solids? |  |
| 5. How do defects in the crystal lattice affect the properties of solids? |  |