Important Trigonometric Functions - 1 Formulas for JEE and NEET
In mathematics, trigonometry is one of the most important topics to learn. Trigonometry is the study of triangles, where "Trigon" means triangle and "metry" means measurement. Below is a list of formulas based on the right triangle that can be used for studying trigonometry.
Trigonometric Ratios
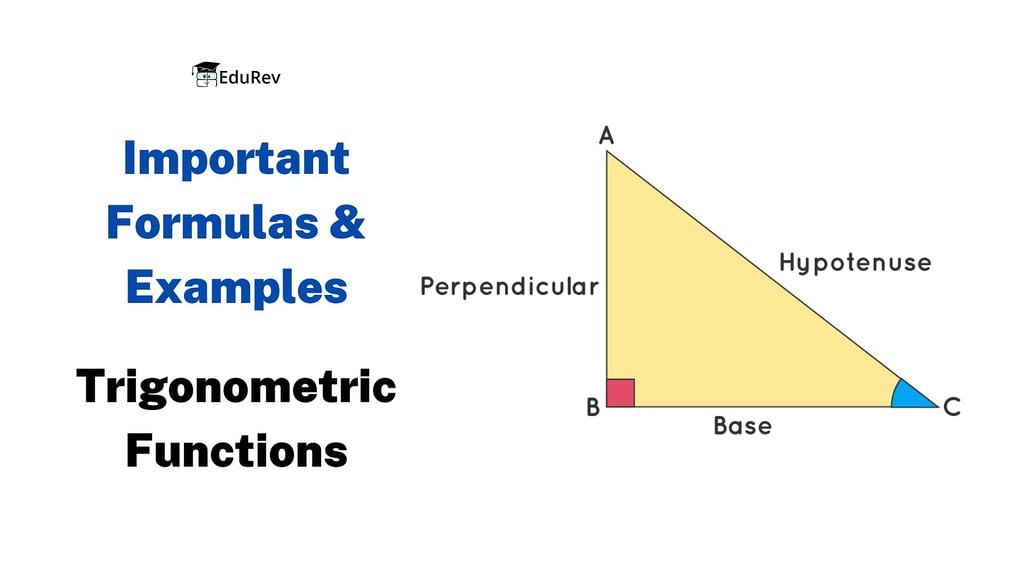
The three main functions in trigonometry are Sine, Cosine and Tangent. They are just the length of one side divided by another
Consider a right-angled triangle with an angle θ, a hypotenuse, a side adjacent to angle θ, and a side opposite the angle to angle θ. For a given angle θ each ratio stays the same no matter how big or small the triangle is
- Sine Function: sin(θ) = Opposite Side / Hypotenuse
- Cosine Function: cos(θ) = Adjacent Side / Hypotenuse
- Tangent Function: tan(θ) = Opposite Side / Adjacent Side
When we divide Sine by Cosine we get:
- Cosecant Function: cosec(θ) = Hypotenuse / Opposite
Secant Function: sec(θ) = Hypotenuse / Adjacent
Cotangent Function: cot(θ) = Adjacent / Opposite
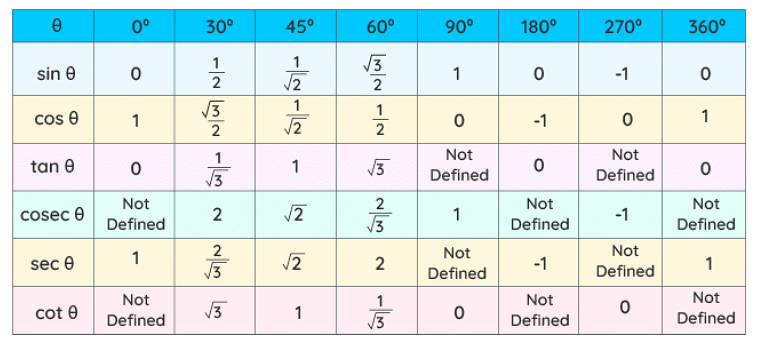
Trigonometric Ratios Table
The trigonometric table is simply a collection of the values of trigonometric ratios for various angles including 0°, 30°, 45°, 60°, 90°, sometimes with other angles like 180°, 270°, and 360° included, in a tabular format.
Here is the trigonometry table for standard angles along with some non-standard angles:
Basic Trigonometric Identities
Tangent and Cotangent Identities
- tan(θ) = sin(θ) / cos(θ)
- cot(θ) = cos(θ) / sin(θ)
Reciprocal Identities
- sin(θ)= 1/cosec(θ)
- cosec(θ) = 1/sin(θ)
- cos(θ) = 1/sec(θ)
- sec(θ) = 1/cos(θ)
- tan(θ) = 1/cot(θ)
- cot(θ) = 1/tan(θ)
Pythagorean Identities
- sin2(θ) + cos2(θ) = 1 ; (-1 ≤ sin θ ≤ 1 ; -1 ≤ cos θ ≤ 1 , θ ∈ R)
- 1 + tan2(θ) = sec2(θ) ; ( |sec θ| ≥ 1, θ ∈ R)
- 1 + cot2(θ) = cosec2(θ) ; (|cosec θ| ≥ 1 , θ ∈ R)
Even and Odd Angle Formulas
- sin(-θ) = -sin(θ)
- cos(-θ) = cos(θ)
- tan(-θ) = -tan(θ)
- cot(-θ) = -cot(θ)
- sec(-θ) = sec(θ)
- cosec(-θ) = -cosec(θ)
Co-function Formulas
- sin(90°-θ) = cos(θ)
- cos(90°-θ) = sin(θ)
- tan(90°-θ) = cot(θ)
- cot(90°-θ) = tan(θ)
- sec(90°-θ) = cosec(θ)
- cosec(90°-θ) = sec(θ)
Important Trigonometric Ratios
- sin nπ = 0 ; cos nπ = (-1)n ; tan nπ = 0 where n ∈ I
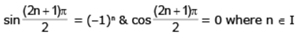
Trigonometric Functions of Allied Angles
If θ is any angle , then - θ, 90 ±θ , 180 ± θ, 270 ± θ , 360 ± θ etc. are called ALLIED ANGLES.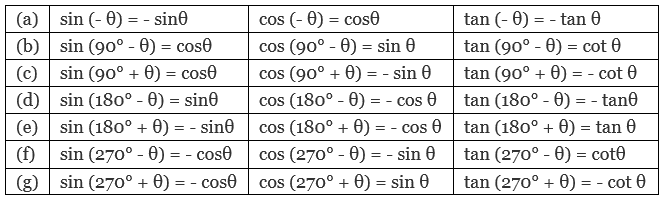
Example 1. Express 1·2 radians in degree measure.
1·2 radians =
Example 2. Calculate sin α if cos α = - 9/11 and α ∈ (π, 3π/2).
For any angle a belonging to the indicated interval sin a is negative, and therefore,
Example 3. Calculate tan α if cos α = √5/5 and α ∈ (π, 3π/2)
For any angle a belonging to the indicated interval tanα is positive and cos a is negative, and therefore
Trigonometric Functions of Sum Or Difference of Two Angles
- sin (A ± B) = sinA cosB ± cosA sinB
- cos (A ± B) = cosA cosB m sinA sinB
- sin²A - sin²B = cos²B - cos²A = sin (A+B) . sin (A- B)
- cos²A - sin²B = cos²B - sin²A = cos (A+B) . cos (A - B)
Factorisation of the Sum Or Difference of Two sines Or cosines:
- sinC + sinD = 2 sin (C + D/2) cos (C - D/2)
- sinC - sinD = 2 cos (C + D/2) sin (C - D/2)
- cosC + cosD = 2 cos (C + D/2) cos (C - D/2)
- cosC - cosD = - 2 sin (C + D/2) sin (C - D/2)
Transformation of Products Into Sum Or Difference Of sines & cosines:
- 2sinAcosB = sin(A+B) + sin(A-B)
- 2cosAsinB = sin(A+B) - sin(A-B)
- 2cosAcosB = cos(A+B) + cos(A-B)
- 2sinAsinB = cos(A-B) - cos(A+B)
Example 4. Suppose x and y are real numbers such that tan x + tan y = 42 and cot x + cot y = 49. Find the value of tan(x + y).
tan x + tan y = 42 and cot x + cot y = 49
now, cot x + cot y = 49
Example 5. If x sinθ = y sin(θ + 2π/3) = z sin (θ + 4π/3) then:
(a) x + y + z = 0
(b) xy + yz + zx = 0
(c) xyz + x + y + z = 1
(d) none
Correct Answer is Option (b)
= xy + yz + zx = 0
Example 6. Find θ satisfying the equation, tan 15° . tan 25° . tan 35° = tan 0, where θ ∈ (0, 15°).
LHS = tan 15° . tan (30° - 5°) . tan (30° + 5°)
let t = tan 30° and m = tan 5°
Example 7. If tan A & tan B are the roots of the quadratic equation, a x2 + b x + c = 0 then evaluate a sin2 (A + B) + b sin (A + B) . cos (A + B) + c cos2 (A + B).
Now E = cos2 (A + B) [a tan2 (A + B) + b tan (A + B) + c]
Example 8. Show that cos2A + cos2(A + B) + 2 cosA cos(180° + B) · cos(360° + A + B) is independent of A. Hence find its value when B = 810°.
cos2A + cos2(A + B) - [2 cosA · cosB · cos (A + B)]
= cos2A + cos2(A + B) - [ {cos(A + B) + cos(A - B) } cos (A + B) ]
= cos2A + cos2(A + B) - cos2(A + B) - (cos2A - sin2B)
= sin2B which is independent of A
now, sin2(810°) = sin2(720° + 90°) = sin290° = 1
Multiple Angles & Sub-Multiple Angles
- sin 2A = 2 sinA cosA ; sin θ = 2 Sin(θ/2)Cos(θ/2)
- cos 2A = cos²A - sin²A = 2cos²A - 1 = 1 - 2 sin²A ;
cos θ= cos² θ/2 - sin² θ/2 = 2cos² θ/2 - 1 = 1 - 2sin² θ/2.
2 cos²A = 1 + cos 2A , 2sin²A = 1 - cos 2A
2 cos² θ/2 = 1 + cos θ, 2 sin² θ/2 = 1 - cos θ. -
- cos 3A = 4 cos3A - 3 cosA
- sin 3A = 3 sinA - 4 sin3A
-
Conditional Identities
If A+B+C = π
- tanA + tanB + tanC = tanA tanB tanC
- sin2A + sin2B + sin2C = 4 sinA sinB sinC
- sinA + sinB + sinC = 4 cos A/2 Cos B/2 Cos C/2
- cos 2A + cos 2B + cos 2C = –1 – 4 cos A cos B cos C
- cos A + cos B + cos C = 1 + 4 sin A/2 sin B/2 sin C/2
Example 10. If A + B + C = π, prove that,
Solution:
Example 11. If A + B + C = θ and cotθ = cot A + cot B + cot C, show that , sin(A-θ). sin (B-θ).sin (C-θ)= sin3 θ.
Solution:
Given cot θ = cot A + cot B + cot C or cot θ - cot A = cot B + cot C
....(1)
....(2)
....(3)
Multiplying (1) , (2) and (3) we get the result
Example 12. Find whether a triangle ABC can exist with the tangents of its interior angle satisfying, tan A = x, tan B = x + 1, and tan C = 1 - x for some real value of x. Justify your assertion with adequate reasoning.
Solution:
In a triangle ∑ tan A = π tan A (to be proved)
x + x + 1 + 1 – x = x(1 + x)(1 – x)
2 + x = x – x3; x3 = –2, x = -21/3
Hence tanA = x < 0 and tanB = x + 1 = 1 – 21/3 < 0
Hence A and B both are obtuse. Which is not possible in a triangle. Hence no such triangle can exist.
Maximum & Minimum values of Trigonometric Functions
- Min. value of a2 tan2 θ + b2 cot2θ = 2ab
- Max and Min. value of acosθ + bsinθ are
- If f(θ) = acos(α + q) + bcos(β + q) where a, b, α and β are known quantities then
-
(constant) then the maximum values of the expression cosα cosβ, cosα+ cosβ, sinα + sinβ and sina sinb occurs when α = β = σ/2
- If A, B, C are the anlges of a triangle then maximum value of sinA + sinB + sinC and sinA sinB sinC occurs when A = B = C = 60º
- In case a quadratic in sinq or cosq is given then the maximum or minimum values can be interpreted by making a perfect square
Example 13. Find the greatest value of c such that system of equations x2 + y2 = 25; x + y = c has a real solution.
Solution:
Put x = 5 cosθ and y = 5 sinθ
5(cosθ+ sinθ) = c; but (cosθ + sinθ)max = √2 and (cosθ + sinθ)min = – √2
hence, cmax = 5√2
Example 14. Find the minimum and maximum value of f (x, y) = 7x2 + 4xy + 3y2 subjected to x2 + y2 = 1.
Solution:
Let x = cosθ and y = sinθ
y = f (θ) = 7 cos2θ + 4 sin θcosθ + 3 sin2θ = 3 + 2 sin 2q + 2(1 + cos 2θ)
= 5 + 2(sin 2θ + cos 2θ) but -√2 ≤ (sin 2θ + cos 2θ) ≤ √2
ymax = 5 + 2√2 and ymin = 5 – 2√2
|
73 videos|264 docs|91 tests
|
FAQs on Important Trigonometric Functions - 1 Formulas for JEE and NEET
| 1. What are the basic trigonometric identities? |  |
| 2. How do you find the trigonometric functions of allied angles? |  |
| 3. What are some examples of multiple angles in trigonometry? |  |
| 4. How do you determine the maximum and minimum values of trigonometric functions? |  |
| 5. What are some important conditional identities in trigonometry? |  |