Ellipse | Mathematics (Maths) for JEE Main & Advanced PDF Download
Standard Equation & Definition
Standard equation of an ellipse referred to its principal axes along the co-ordinate axes is
 +
+  = 1. where a > b & b2 = a2 (1 - e2) ⇒ a2 - b2 = a2 e2.
= 1. where a > b & b2 = a2 (1 - e2) ⇒ a2 - b2 = a2 e2.
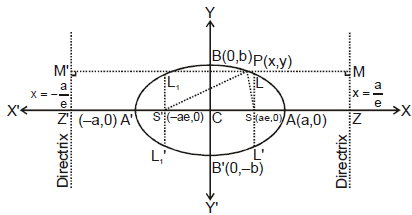
where e = eccentricity (0 < e < 1).
FOCI : S  (ae, 0) & S'
(ae, 0) & S'  (- ae, 0).
(- ae, 0).
(a) Equation of directrices :

(b) Vertices :
A'  (-a, 0) & A
(-a, 0) & A 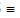 (a, 0)
(a, 0)
(c) Major axis : The line segment A' A in which the foci S' S S lie is of length 2a & is called the major axis (a > b) of the ellipse. Point of intersection of major axis with directrix is called the foot of the directrix (z)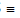
 .
.
(d) Minor Axis : The y-axis intersects the ellipse in the points B' 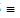 (0, - b) & B
(0, - b) & B 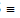 (0, b). The line segment B'B of length 2b (b < a) is called the Minor Axis of the ellipse.
(0, b). The line segment B'B of length 2b (b < a) is called the Minor Axis of the ellipse.
(e) Principal Axes : The major & minor axis together are called Principal Axes of the ellipse.
(f) Centre : The point which bisects every chord of the conic drawn through it is called the centre of the conic. C  (0, 0) the origin is the centre of the ellipse
(0, 0) the origin is the centre of the ellipse  +
+  = 1
= 1
(g) Diameter : A chord of the conic which passes through the centre is called a diameter of the conic.
(h) Focal Chord : A chord which passes through a focus is called a focal chord.
(i) Double Ordinate : A chord perpendicular to the major axis is called a double ordinate.
(j) Latus Rectum : The focal chord perpendicular to the major axis is called the latus rectum.
(i) Length of latus rectum (LL') =  =
=  = 2a(1 - e2) = 2e
= 2a(1 - e2) = 2e
(ii) Equation of latus rectum : x = ± ae.
(iii) Ends of the latus rectum are  and L1'
and L1' .
.
(k) Focal radii : SP = a -ex and S'P = a + ex ⇒ SP + S'P = 2a = Major axis.
(l) Eccentricity : e = 
Note :
(i) The sum of the focal distances of any point on the ellipse is equal to the major axis. Hence distance of focus from the extremity of a minor axis is equal to semi major axis. i.e. BS = CA.
(ii) If the equation of the ellipse is given as  +
+  = 1 & nothing is mentioned, then the rule is to assume that a > b.
= 1 & nothing is mentioned, then the rule is to assume that a > b.
Ex.1 If LR of an ellipse is half of its minor axis, then its eccentricity is
Sol.
As given  = b ⇒ 2b = a
= b ⇒ 2b = a
⇒ 4b2 = a2 ⇒ 4a2(1 - e2) = a2
⇒ 1 - e2 = 1/4  e =
e = 
Ex.2 Find the equation of the ellipse whose foci are (2, 3), (-2, 3) and whose semi minor axis is of length  .
.
Sol. Here S is (2, 3) & S' is (-2, 3) and 
⇒ SS' = 4 = 2ae ⇒ ae = 2
but b2 = a2 (1 - e2) ⇒ 5 = a2 - 4
⇒ a = 3. Hence the equation to major axis is y = 3
Centre of ellipse is midpoint of SS' i.e. (0, 3)
 Equation to ellipse is
Equation to ellipse is  +
+  = 1 or
= 1 or  +
+  = 1
= 1
Ex.3 Find the equation of the ellipse having centre at (1, 2), one focus at (6, 2) and passing through the point (4, 6).
Sol.
With centre at (1, 2), the equation of the ellipse is  +
+  = 1.
= 1.
It passes through the point (4, 6) ⇒  +
+  = 1 .............(i)
= 1 .............(i)
Distance between the focus and the centre = (6 - 1) = 5 = ae
⇒ b2 = a2 - a2e2 = a2 - 25 .............(ii)
Solving for a2 and b2 from the equation (i) and (ii), we get a2 = 45 and b2 = 20.
Hence the equation of the ellipse is  +
+  = 1
= 1
B. Another form of Ellipse
 +
+  = 1, (a < b)
= 1, (a < b)
(a) AA' = Minor axis = 2a
(b) BB' = Major axis = 2b
(c) a2 = b2 (1 - e2)
(d) Latus rectum LL' = L1L1' =  .
.
equation y = ± be
(e) Ends of the latus rectum are :
 ,
,

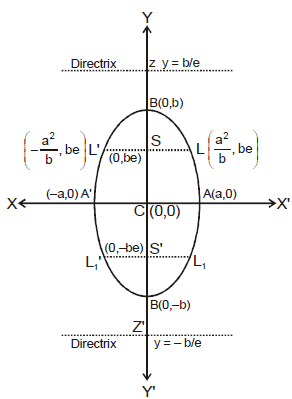
(f) Equation of directrix y = ±  .
.
(g) Eccentricity : e = 
Ex.4 The equation of the ellipse with respect to coordinate axes whose minor axis is equal to the distance between its foci and whose LR = 10, will be
Sol. When a > b
As given 2b = 2ae ⇒ b = ae ............(i)
Also  = 10 ⇒b2 = 5a . ...........(ii)
= 10 ⇒b2 = 5a . ...........(ii)
Now since b2 = a2 - a2e2 ⇒ b2 = a2 - b2 ⇒ 2b2 = a2 ............(iii) [From (i)]
(ii), (iii) ⇒ a2 = 100, b2 = 50
Hence equation of the ellipse will be  +
+  = 1 ⇒ x2 + 2y2 = 100
= 1 ⇒ x2 + 2y2 = 100
Similarly when a < b then required ellipse is 2x2 + y2 = 100
C. General Equation of an Ellipse
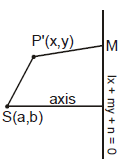
Let (a, b) be the focus S, and lx + my + n = 0 is the equation of directrix.
Let P(x, y) be any point on the ellipse. Then by definition.
⇒ SP = e PM (e is the eccentricity)
⇒ (x - a)2 + (y - b)2 = e2
⇒ (l2 + m2) {(x - a)2 + (y - b)2} = e2{lx + my + n}2
D. Auxilliary Circle/eccentric Angle
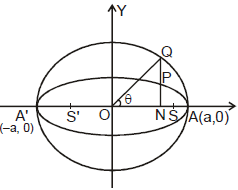
A circle described on major axis as diameter is called the auxilliary circle. Let Q be a point on the auxilliary circle x2 + y2 = a2 such that QP produced is perpendicular to the x-axis then P & Q are called as the corresponding points on the ellipse & the auxilliary circle respectively. `θ' is called the eccentric angle of the point P on the ellipse 
Note that : =
=  =
= 
Hence "If from each point of a circle perpendiculars are drawn upon a fixed diameter then the locus of the points dividing these perpendiculars in a given ratio is an ellipse of which the given circle is the auxilliary circle".
E. position of a point w.r.t an ellipse
The point P(x1, y1) lies outside, inside or on the ellipse according as ;  +
+  - 1 > < or = 0.
- 1 > < or = 0.
F. Line and an ellipse
The line y = mx + c meets the ellipse  +
+  = 1 in two points real, coincident or imaginary according as c2 is < = or > a2m2 + b2.
= 1 in two points real, coincident or imaginary according as c2 is < = or > a2m2 + b2.
Hence y = mx + c is tangent to the ellipse  +
+  = 1 if c2 = a2m2 + b2.
= 1 if c2 = a2m2 + b2.
The equation to the chord of the ellipse joining two points with eccentric angles a & b is given by  cos
cos  +
+  sin
sin  = cos
= cos  .
.
G. Parametric representation
The equations x = cosθ & y = b sinθ together represent the ellipse  +
+  = 1
= 1
where θ is a parameter (eccentric angle).
Note that : If P(θ ) ≡ (a cosθ, b sinθ) is on the ellipse then ;
Q(θ ) ≡ (a cosθ, a sinθ) is on the auxilliary circle.
Ex.5 For what value of l does the line y = x + l touches the ellipse 9x2 + 16y2 = 144.
Sol. Equation of ellipse is 9x2 + 16y2 = 144 or
Equation of ellipse is 9x2 + 16y2 = 144 or  +
+  = 1
= 1
Comparing this with  +
+  = 1 then we get a2 = 16 and b2 = 9
= 1 then we get a2 = 16 and b2 = 9
and comparing the line y = x + λ with y = mx + c
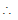 m = 1 and c = λ
m = 1 and c = λ
If the line y = x + λ touches the ellipse 9x2 + 16y2 = 144, then c2 = a2m2 + b2
⇒ λ2 = 16 × 12 + 9
⇒ λ2 = 25
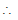 λ = ± 5
λ = ± 5
Ex.6 If α, β are eccentric angles of end points of a focal chord of the ellipse  +
+  = 1, then tan α/2. tan β/2 is equal to
= 1, then tan α/2. tan β/2 is equal to
Sol.
Equation of line joining points `α' and `β' is cos  +
+  sin
sin  = cos
= cos 
If it is a focal chord, then it passes through focus (ae, 0), so e cos  = cos
= cos 
⇒  =
= 
⇒  =
= 
⇒  =
= 
⇒ tan tan
tan =
= 
H. Director Circle
Locus of the point of intersection of the tangents which meet at right angles is called the Director Circle. The equation to this locus is x2 + y2 = a2 + b2 i.e. a circle whose centre is the centre of the ellipse & whose radius is the length of the line joining the ends of the major & minor axis.
Ex.7 A tangent to the ellipse x2 + 4y2 = 4 meets the ellipse x2 + 2y2 = 6 at P and Q. Prove that the tangents at P and Q of the ellipse x2 + 2y2 = 6 are at right angles.
Sol.
Given ellipse are  +
+  = 1 ...........(i)
= 1 ...........(i)
and,  +
+  = 1 ...........(ii)
= 1 ...........(ii)
any tangent to (i) is  +
+  = 1 ...........(iii)
= 1 ...........(iii)
It cuts (ii) at P and Q, and suppose tangent at P and Q meet at (h, k) Then equation of chord of contact of (h, k) with respect to ellipse (ii) is  +
+  = 1 ...........(iv)
= 1 ...........(iv)
comparing (iii) and (iv), we get  =
=  = 1
= 1
⇒ cosθ =  and sinθ =
and sinθ = 
⇒ h2 + k2 = 9
locus of the point (h, k) is x2 + y2 = 9
⇒ x2 + y2 = 6 + 3 = a2 + b2
i.e. director circle of second ellipse. Hence the tangents are at right angles.
I. Tangent to the Ellipse  +
+  = 1
= 1
(a) Point form : Equation of tangent to the given ellipse at its point (x1, y1) is  +
+  = 1
= 1
Note : For general ellipse replace x2 by xx1,y2by yy1,2x by x + x1,2y by y + y1,2xy by xy1+yx1 & c by c.
(b) Slope form : Equation of tangent to the given ellipse whose slope is `m', is y = mx ± 
Point of contact are 
Note : There are two tangents to the ellipse having the same m, i.e. there are two tangents parallel to any given direction.
(c) Parametric form : Equation of tangent to the given ellipse at its point (a cosθ, b sinθ), is
 +
+  = 1
= 1
Note :
(i) The eccentric angles of point of contact of two parallel tangents differ by π.
(ii) Point of intersection of the tangents at the point α & β is 
Ex.8 Find the equations of the tangents to the ellipse 3x2 + 4y2 = 12 which are perpendicular to the line y + 2x = 4.
Sol. Let m be the slope of the tangent, since the tangent is perpendicular to the line y + 2x = 4.
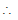 mx - 2 = - 1
mx - 2 = - 1
m = 1/2
Since 3x2 + 4y2 = 12 or  +
+  = 1.
= 1.
Comparing this with  +
+  = 1
= 1
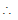 a2 = 4 and b2 = 3
a2 = 4 and b2 = 3
So the equation of the tangent are 

or
x - 2y ± 4 = 0.
Ex.9 The tangent at a point P on an ellipse intersects the major axis in T and N is the foot of the perpendicular from P to the same axis. Show that the circle drawn on NT as diameter intersects the auxilliary circle orthogonally.
Sol.
Let the equation of the ellipse be  +
+  = 1. Let (acosθ, bsinθ) be a point on the ellipse. The equation of the tangent at P is
= 1. Let (acosθ, bsinθ) be a point on the ellipse. The equation of the tangent at P is  +
+  = 1. It meets the major axis at T ≡ (a secθ, 0). The coordinates of N are (a cosθ, 0). The equation of the circle with NT as its diameter is (x - asecθ) (x - acosθ) + y2 = 0 ⇒ x2 + y2 - ax(secθ + cosθ) + a2 = 0
= 1. It meets the major axis at T ≡ (a secθ, 0). The coordinates of N are (a cosθ, 0). The equation of the circle with NT as its diameter is (x - asecθ) (x - acosθ) + y2 = 0 ⇒ x2 + y2 - ax(secθ + cosθ) + a2 = 0
It cuts the axuilliary circle x2 + y2 - a2 = 0 orthogonally if 2g . 0 + 2f . 0 = a2 - a2 = 0. which is true.
J. Normal to the Ellipse  +
+  = 1
= 1
(a) Point form : Equation of the normal to the given ellipse at (x1, y1) is  -
-  = a2 - b2 = a2e2
= a2 - b2 = a2e2
(b) Slope form : Equation of a normal to the given ellipse whose slope is `m' is y = mx 
(c) Parametric form : Equation of the normal to the given ellipse at the point (acosθ, bsinθ) is ax. sec θ - by. cosec θ = (a2 - b2).
Ex.10 Find the condition that the line lx + my = n may be a normal to the ellipse  +
+  = 1.
= 1.
Sol.
Equation of normal to the given ellipse at (a cosθ, b sinθ) is  -
-  = a2 - b2 ..........(i)
= a2 - b2 ..........(i)
If the line lx + my = n is also normal to the ellipse then there must be a value of θ for which line (i) and line lx + my = n are identical. For the value of q we have
 or
or  cosθ =
cosθ =  ........(iii)
........(iii)
and sinθ =  .....(iv)
.....(iv)
Squaring and adding (iii) and (iv), we get 1 = 
 which is the required condition.
which is the required condition.
Ex.11 If the normal at an end of a latus-rectum of an ellipse  +
+  = 1 passes through one extremity of the minor axis, show that the eccentricity of the ellipse is given by e =
= 1 passes through one extremity of the minor axis, show that the eccentricity of the ellipse is given by e = 
Sol. The co-ordinates of an end of the latus-rectum are (ae, b2/a). The equation of normal at P(ae, b2/a) is
 -
-  = a2 - b2
= a2 - b2
or
 - ay = a2 - b2
- ay = a2 - b2
It passes through one extremity of the minor axis whose co-ordinates are (0, -b)
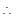 0 + ab = a2 - b2
0 + ab = a2 - b2
⇒ (a2b2) = (a2 - b2)2
⇒ a2.a2(1 - e2) = (a2 e2)2
⇒ 1 - e2 + e4
⇒ e4 + e2 - 1 = 0
⇒ (e2)2 + e2 - 1 = 0
 e2 =
e2 =  ⇒ e =
⇒ e =  (taking positive sign)
(taking positive sign)
Ex.12 P and Q are corresponding points on the ellipse  +
+  = 1 and the auxilliary circles respectively. The normal at P to the ellipse meets CQ in R, where C is the centre of the ellipse, Prove that CR = a + b
= 1 and the auxilliary circles respectively. The normal at P to the ellipse meets CQ in R, where C is the centre of the ellipse, Prove that CR = a + b
Sol. Let P 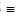 (acosθ, bsinθ)
(acosθ, bsinθ)
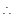 Q
Q 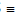 (acosθ, asinθ)
(acosθ, asinθ)
Equation of normal at P is (asecq) x - (bcosecθ)y = a2 - b2 ............(i)
equation of CQ is y = tanθ . x ............(ii)
Solving equation (i) & (ii), we get
(a - b)x = (a2 - b2) cosθ
⇒ x = (a + b) cosθ, & y = (a + b) sinθ
 R
R  (a + b)cosθ, (a + b)sinθ
(a + b)cosθ, (a + b)sinθ
 CR = a + b
CR = a + b
K. Pair of tangents
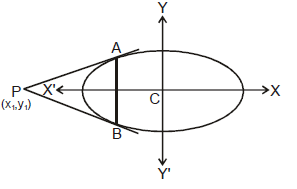
If P(x1, y1) be any point lies outside the ellipse  +
+  = 1,
= 1,
and a pair of tangents PA, PB can be drawn to it from P.
Then the equation of pair of tangents of PA and PB is SS1 = T2
where S1 =  +
+  - 1, T =
- 1, T =  +
+  - 1
- 1
i.e. 
 =
= 
L. Chord of contact
If PA and PB be the tangents from point P(x1, y1) to the ellipse  +
+  = 1.
= 1.
Then the equation of the chord of contact AB is  +
+  = 1 or T = 0 (at x1, y1)
= 1 or T = 0 (at x1, y1)
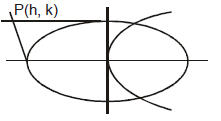
Ex.13 If tangents to the parabola y2 = 4ax intersect the ellipse  +
+  = 1 at A and B, the find the locus of point of intersection of tangents at A and B.
= 1 at A and B, the find the locus of point of intersection of tangents at A and B.
Sol. Let P ≡ (h, k) be the point of intersection of tangents at A & B
 equation of chord of contact AB is
equation of chord of contact AB is  +
+  = 1 ..............(i)
= 1 ..............(i)
which touches the parabola.
Equation of tangent to parabola y2 = 4ax is y = mx +  ⇒ mx - y = -
⇒ mx - y = - ..............(ii)
..............(ii)
equation (i) & (ii) as must be same
 ⇒ m = -
⇒ m = -
 & m =
& m = 
 -
- =
=  ⇒ locus of P is y2 = -
⇒ locus of P is y2 = -  .x
.x
M. Equation of chord with mid point (x1, y1)
The equation of the chord of the ellipse  +
+  = 1, whose mid-point be (x1, y1) is T = S1
= 1, whose mid-point be (x1, y1) is T = S1
where T =  +
+  - 1, S1 =
- 1, S1 =  +
+  - 1 i.e.
- 1 i.e. 
Ex.14 Find the locus of the mid - point of focal chords of the ellipse  +
+  = 1.
= 1.
Sol. Let P  (h, k) be the mid - point
(h, k) be the mid - point
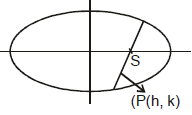
 equation of chord whose mid-point is given
equation of chord whose mid-point is given  +
+  - 1 =
- 1 =  +
+  - 1 since it is focal chord,
- 1 since it is focal chord,
 It passes through focus, either (ae, 0) or (-ae, 0)
It passes through focus, either (ae, 0) or (-ae, 0)
If it passes through (ae, 0)
 locus is
locus is  =
=  +
+ 
If it passes through (-ae, 0)
 locus is -
locus is -  =
=  +
+ 
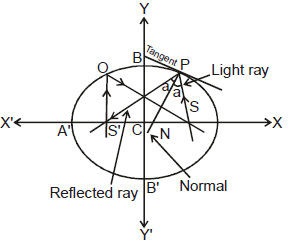
N. Important Highlights
Referring to an ellipse  +
+  = 1
= 1
(a) If P be any point on the ellipse with S & S'
as its foci then l(SP) + l(S'P) = 2a.
(b) The tangents & normal at a point P on the ellipse bisect the external & internal angles between the focal distances of P.
This refers to the well known reflection property of the ellipse which states that rays from one focus are reflected through other focus & vice versa. Hence we can deduce that the straight lines joining each focus to the foot of the perpendicular from the other focus upon the tangent at any point P meet on the normal PG and bisects it where G is the point where normal at P meets the major axis.
(c) The product of the length's of the perpendicular segments from the foci on any tangent to the ellipse is b2 and the feet of these perpendiculars lie on its auxiliary circle and the tangents at these feet to the auxiliary circle meet on the ordinate of P and that the locus of their point of intersection is a similar ellipse as that of the original one.
(d) The portion of the tangent to an ellipse between the point of contact & the directrix subtends a right angle at the corresponding focus.
(e) If the normal at any point P on the ellipse with centre C meet the major & minor axes in G & g respectively, & if CF be perpendicular upon this normal, then
(i) PF . PG = b2
(ii) PF . Pg = a2
(iii) PG . Pg = SP . S'P
(iv) CG . CT = CS2
(v) locus of the mid point of Gg is another ellipse having the same eccentricity as that of the original ellipse.
[where S and S' are the focii of the ellipse and T is the point where tangent at P meet the major axis]
(f) The circle on any focal distance as diameter touches the auxilliary circle.
(g) Perpendiculars from the centre upon all chords which join the ends of any perpendicular diameters of the ellipse are of constant length.
(h) If the tangent at the point P of a standard ellipse meets the axes in T and t and CY is the perpendicular on it form the centre then,
(i) T t . PY = a2 - b2 and
(ii) least value of T t is a + b.
|
209 videos|447 docs|187 tests
|
FAQs on Ellipse - Mathematics (Maths) for JEE Main & Advanced
| 1. What is an ellipse in geometry? |  |
| 2. How is the length of the major and minor axes of an ellipse calculated? |  |
| 3. What is the eccentricity of an ellipse? |  |
| 4. How is the area of an ellipse calculated? |  |
| 5. Can an ellipse have a negative area? |  |


















