Introduction to Integrals | Mathematics (Maths) for JEE Main & Advanced PDF Download
Integral Calculus
- Integral Calculus is the branch of calculus where we study integrals and their properties.
- Integration is a very important concept which is the inverse process of differentiation. Both the integral calculus and the differential calculus are related to each other by the fundamental theorem of calculus.
- If we know the f’ of a function that is differentiable in its domain, we can then calculate f. In differential calculus, we used to call f’, the derivative of the function f. Here, in integral calculus, we call f as the anti-derivative or primitive of the function f’. And the process of finding the anti-derivatives is known as anti-differentiation or integration.
- Integration can be classified into two different categories:
(i) Definite Integral
(ii) Indefinite Integral
Definite Integral
- An integral that contains the upper and lower limits i.e. start and end value, then it is known as a definite integral. On a real line, x is restricted to lie. Definite Integral is also called a Riemann Integral when it is restricted to lie on the real line.
- A definite Integral is represented as:
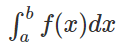
Indefinite Integral
- Indefinite integrals are not defined using the upper and lower limits. It represents the family of the given function whose derivatives are f. It returns a function of the independent variable.
- The integration of a function f(x) is given by F(x) and it is represented by:
∫f(x) dx = F(x) + C, where R.H.S. of the equation means integral of f(x) with respect to x.
F(x) = Anti-derivative or primitive
f(x) = Integrand
dx = Integrating agent.
C = Constant of integration.
x = Variable of integration. - It may seem strange that there exists an infinite number of anti-derivatives for a function f.
Example: Let us take f’ (x) = 3x2.
By hit and trial, we can find out that its anti-derivative is F(x) = x3 because if you differentiate F with respect to x, you will get 3x2.
There is only one function that we got as the anti-derivative of f(x).
If we differentiate G(x) = x3+ 9 with respect to x, we would get the same derivative i.e. f(x). - This gives us an important insight. Since the differentiation of all the constants is zero, we can write any constant with F(x) and the derivative would still be equal to f(x). Thus, there are infinite constants that can be substituted for C in the equation
Hence, there are infinite functions whose derivative is equal to f. C is called an arbitrary constant or the constant of integration.
Properties of Indefinite Integrals:
(i) The process of differentiation and integration are inverses of each other.
i.e. 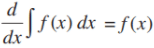 and
and 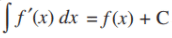
(ii) Two indefinite integrals with the same derivative lead to the same family of curves, and so they are equivalent.
(iii) The integral of the sum of two functions is equal to the sum of integrals of the given functions,
i.e.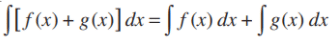
(iv) For any real value of p,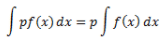
(v) For a finite number of functions f1, f2 …. fn and the real numbers p1, p2…pn,
∫[p1f1(x) + p2f2(x)….+pnfn(x) ]dx = p1∫f1(x)dx + p2∫f2(x)dx + ….. + pn∫fn(x)dx
Methods of Integration
1. Integration by substitution: In this method the integral ∫f(x)dx is expressed in terms of another integral where some other variables say t is the independent variable; x and t being connected by some suitable relation x=g(t).
It leads to the result ∫f(x)dx=∫f(g(t)). g'(t) dt
2. Integration by parts: This method is used to integrate the product of two functions. If f(x) and g(x) are two integrable functions, then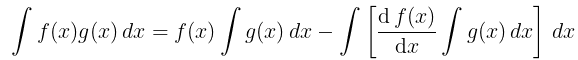
i.e. The integral of (product of two functions) = first function * integral of the second - integral of (derivative of first function * integral of the second function)
In order to select the first function, the following order is followed:
Inverse → Logarithmic → Algebraic → Trigonometric → Exponential
3. Integration by a partial fraction: If the integral is in the form of an algebraic fraction that cannot be integrated then the fraction needs to be decomposed into partial fractions.
Rules for expressing in partial fraction:
- The numerator must be at least one degree less than the denominator.
- For every factor (ax+b) in the denominator, there is a partial fraction
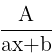
- If a factor is repeated in the denominator n times then that partial fraction should be written n times with degree 1 through n
- For a factor of the form (ax²+bx+c) in the denominator, there will be a partial fraction of the form
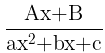
Uses of Integral Calculus
Integral Calculus is mainly used for the following two purposes:
- To calculate f(x) from f’(x). If a function f is differentiable in the interval of consideration, then f’ is defined in that interval. We have already seen in differential calculus how to calculate derivatives of a function. We can “undo” that with the help of integral calculus.
- To calculate the area under a curve.
Until now, we have learned that areas are always positive. But as a matter of fact, there is something called a signed area.
Integral Calculus Formulas
We had differentiation formulas, we have integral formulas as well. Let us go ahead and look at some of the integral calculus formulas.
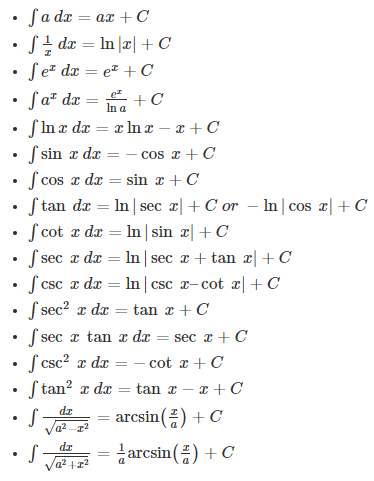
Application of Integral Calculus
The important application of integral calculus are as follow:
- The area between two curves
- Centre of mass
- Kinetic energy
- Surface area
- Work
- Distance, velocity and acceleration
- The average value of a function
- Volume
- Probability
Integral Calculus Examples
Example: Find the integral for the for the following function.
(i) f(x) = √x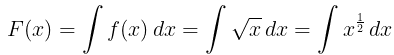
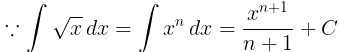
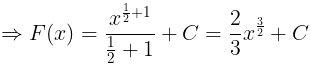
(ii) f(x) =cos2x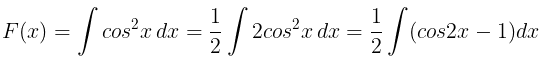
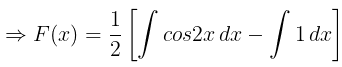
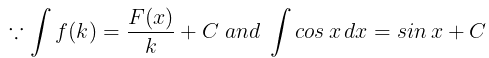
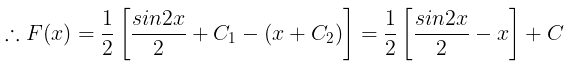
|
176 videos|582 docs|160 tests
|
FAQs on Introduction to Integrals - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the difference between definite and indefinite integrals in integral calculus? |  |
| 2. What are some common methods of integration used in integral calculus? |  |
| 3. How is integral calculus used in real-world applications, particularly in commerce? |  |
| 4. Can you provide some examples of integral calculus applications in commerce? |  |
| 5. What are some key integral calculus formulas that are frequently used in commerce applications? |  |






















