NCERT Solutions Class 11 Maths Chapter 2 - Relations and Functions
Exercise 1.1
Q1: Determine whether each of the following relations are reflexive, symmetric and transitive:
(i) Relation R in the set A = {1, 2, 3…13, 14} defined as
R = {(x, y): 3x − y = 0}
(ii) Relation R in the set N of natural numbers defined as
R = {(x, y): y = x + 5 and x < 4}
(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as
R = {(x, y): y is divisible by x}
(iv) Relation R in the set Z of all integers defined as
R = {(x, y): x − y is as integer}
(v) Relation R in the set A of human beings in a town at a particular time given by
(a) R = {(x, y): x and y work at the same place}
(b) R = {(x, y): x and y live in the same locality}
(c) R = {(x, y): x is exactly 7 cm taller than y}
(d) R = {(x, y): x is wife of y}
(e) R = {(x, y): x is father of y}
Ans:
(i) A = {1, 2, 3 … 13, 14}
R = {(x, y): 3x − y = 0}
∴ R = {(1, 3), (2, 6), (3, 9), (4, 12)}
R is not reflexive since (1, 1), (2, 2) … (14, 14) ∉ R.
Also, R is not symmetric as (1, 3) ∈ R, but (3, 1) ∉ R. [3(3) − 1 ≠ 0]
Also, R is not transitive as (1, 3), (3, 9) ∈ R, but (1, 9) ∉ R. [3(1) − 9 ≠ 0]
Hence, R is neither reflexive, nor symmetric, nor transitive.
(ii) R = {(x, y) : y = x + 5 and x < 4} = {(1, 6), (2, 7), (3, 8)}
It is clear that (1, 1) ∉ R.
∴ R is not reflexive.
(1, 6) ∈ R But, (1, 6) ∉ R.
∴ R is not symmetric.
Now, since there is no pair in R such that (x, y) and (y, z) ∈ R, then (x, z) cannot belong to R.
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
(iii) A = {1, 2, 3, 4, 5, 6}
R = {(x, y): y is divisible by x}
We know that any number (x) is divisible by itself.
So, (x, x) ∈ R
∴ R is reflexive.
Now,
(2, 4) ∈ R [as 4 is divisible by 2]
But, (4, 2) ∉ R. [as 2 is not divisible by 4]
∴ R is not symmetric.
Let (x, y), (y, z) ∈ R. Then, y is divisible by x and z is divisible by y.
∴ z is divisible by x.
⇒ (x, z) ∈ R
∴ R is transitive.
Hence, R is reflexive and transitive but not symmetric.
(iv) R = {(x, y): x − y is an integer}
Now, for every x ∈ Z, (x, x) ∈ R as x − x = 0 is an integer.
∴ R is reflexive.
Now, for every x, y ∈ Z, if (x, y) ∈ R, then x − y is an integer.
⇒ −(x − y) is also an integer.
⇒ (y − x) is an integer.
∴ (y, x) ∈ R
∴ R is symmetric.
Now,
Let (x, y) and (y, z) ∈ R, where x, y, z ∈ Z.
⇒ (x − y) and (y − z) are integers.
⇒ x − z = (x − y) + (y − z) is an integer.
∴ (x, z) ∈ R
∴ R is transitive.
Hence, R is reflexive, symmetric, and transitive.
(v)
(a) R = {(x, y): x and y work at the same place}
⇒ (x, x) ∈ R [as x and x work at the same place]
∴ R is reflexive.
If (x, y) ∈ R, then x and y work at the same place.
⇒ y and x work at the same place.
⇒ (y, x) ∈ R.
∴ R is symmetric.
Now, let (x, y), (y, z) ∈ R
⇒ x and y work at the same place and y and z work at the same place.
⇒ x and z work at the same place.
⇒ (x, z) ∈ R
∴ R is transitive.
Hence, R is reflexive, symmetric and transitive.
(b) R = {(x, y) : x and y live in the same locality}
Clearly, (x, x) ∈ R as x and x is the same human being.
∴ R is reflexive.
If (x, y) ∈ R, then x and y live in the same locality.
⇒ y and x live in the same locality.
⇒ (y, x) ∈ R
∴ R is symmetric.
Now, let (x, y) ∈ R and (y, z) ∈ R.
⇒ x and y live in the same locality and y and z live in the same locality.
⇒ x and z live in the same locality.
⇒ (x, z) ∈ R
∴ R is transitive.
Hence, R is reflexive, symmetric and transitive.
(c) R = {(x, y): x is exactly 7 cm taller than y}
Now, (x, x) ∉ R
Since, human being x cannot be taller than himself.
∴ R is not reflexive.
Now, let (x, y) ∈ R.
⇒ x is exactly 7 cm taller than y.
Then, y is not taller than x. [Since, y is 7 cm smaller than x]
∴ (y, x) ∉ R
Indeed, if x is exactly 7 cm taller than y, then y is exactly 7 cm shorter than x.
∴ R is not symmetric.
Now,
Let (x, y), (y, z) ∈ R.
⇒ x is exactly 7 cm taller than y and y is exactly 7 cm taller than z.
⇒ x is exactly 14 cm taller than z.
∴ (x, z) ∉ R
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
(d) R = {(x, y): x is the wife of y}
Now,
(x, x) ∉ R
Since x cannot be the wife of herself.
∴ R is not reflexive.
Now, let (x, y) ∈ R
⇒ x is the wife of y.
Clearly y is not the wife of x.
∴ (y, x) ∉ R
Indeed, if x is the wife of y, then y is the husband of x.
∴ R is not transitive.
Let (x, y), (y, z) ∈ R
⇒ x is the wife of y and y is the wife of z.
This case is not possible. Also, this does not imply that x is the wife of z.
∴ (x, z) ∉ R
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
(e) R = {(x, y): x is the father of y}
(x, x) ∉ R
As x cannot be the father of himself.
∴ R is not reflexive.
Now, let (x, y) ∉ R.
⇒ x is the father of y.
⇒ y cannot be the father of y.
Indeed, y is the son or the daughter of y.
∴ (y, x) ∉ R
∴ R is not symmetric.
Now, Let (x, y) ∈ R and (y, z) ∉ R.
⇒ x is the father of y and y is the father of z.
⇒ x is not the father of z.
Indeed x is the grandfather of z.
∴ (x, z) ∉ R
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
Q2: Show that the relation R in the set R of real numbers, defined as R = {(a, b) : a ≤ b2} is neither reflexive nor symmetric nor transitive.
Ans: R = {(a, b) : a ≤ b2}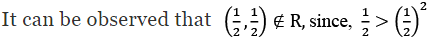
R is not reflexive.
∴ (4, 1) ∉ R
∴ R is not symmetric.
Now,
(3, 2), (2, 1.5) ∉ R
But, 3 > (1.5)2 = 2.25
∴ (3, 1.5) ∉ R
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
Q3: Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.
Ans: Let A = {1, 2, 3, 4, 5, 6}.
A relation R is defined on set A as: R = {(a, b) : b = a + 1}
∴ R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)} we can find (a, a) ∉ R, where a ∈ A.
For instance,
(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) ∉ R
∴ R is not reflexive.
It can be observed that (1, 2) ∈ R, but (2, 1) ∉ R.
∴ R is not symmetric.
Now, (1, 2), (2, 3) ∈ R
But, (1, 3) ∉ R
∴ R is not transitive
Hence, R is neither reflexive, nor symmetric, nor transitive.
Q4: Show that the relation R in R defined as R = {(a, b): a ≤ b}, is reflexive and transitive but not symmetric.
Ans: R = {(a, b) : a ≤ b}
Clearly (a, a) ∈ R [as a = a]
∴ R is reflexive.
Now, (2, 4) ∈ R (as 2 < 4)
But, (4, 2) ∉ R as 4 is greater than 2.
∴ R is not symmetric.
Now, let (a, b), (b, c) ∈ R.
Then, a ≤ b and b ≤ c
⇒ a ≤ c
⇒ (a, c) ∈ R
∴ R is transitive.
Hence R is reflexive and transitive but not symmetric.
Q5: Check whether the relation R in R defined as R = {(a, b) : a ≤ b3} is reflexive, symmetric or transitive.
Ans: R = {(a, b) : a ≤ b3}
It is observed that ( 1/2, 1/2) ∉ R, since, 1/2 > (1/2)3
∴ R is not reflexive.
Now, (1, 2) ∈ R (as 1 < 23 = 8)
But, (2, 1) ∉ R (as 23 > 1)
∴ R is not symmetric.
We have (3, 3/2) , (3/2 , 6/5) ∈ R, since 3 < (3/2)3 and 3/2 < (6/5)3
But (3 , 6/5) ∉ R as 3 > (6/5)3
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
Q6: Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
Ans: Let A = {1, 2, 3}.
A relation R on A is defined as R = {(1, 2), (2, 1)}.
It is clear that (1, 1), (2, 2), (3, 3) ∉ R.
∴ R is not reflexive.
Now, as (1, 2) ∈ R and (2, 1) ∈ R, then R is symmetric.
Now, (1, 2) and (2, 1) ∈ R
However, (1, 1) ∉ R
∴ R is not transitive.
Hence, R is symmetric but neither reflexive nor transitive.
Q7: Show that the relation R in the set A of all the books in a library of a college, given by R = {(x, y): x and y have same number of pages} is an equivalence relation.
Ans: Set A is the set of all books in the library of a college.
R = {x, y): x and y have the same number of pages}
Now, R is reflexive since (x, x) ∈ R as x and x has the same number of pages.
Let (x, y) ∈ R
⇒ x and y have the same number of pages.
⇒ y and x have the same number of pages.
⇒ (y, x) ∈ R
∴ R is symmetric.
Now, Let (x, y) ∈ R and (y, z) ∈ R.
⇒ x and y and have the same number of pages and y and z have the same number of pages.
⇒ x and z have the same number of pages.
⇒ (x, z) ∈ R
∴ R is transitive.
Hence, R is an equivalence relation.
Q8: Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b): |a - b| is even}, is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.
Ans: A = {1, 2, 3, 4, 5} and R={(a, b): |a - b| is even}
It is clear that for any element a ∈ A, we have|a - a|= 0 (which is even).
∴ R is reflexive.
Let (a, b) ∈ R.
⇒ |a - b| is even
⇒ |-(a - b)| = |b - a| is also even
⇒ (b, a) ∈ R
∴ R is symmetric.
Now, let (a, b) ∈ R and (b, c) ∈ R.
⇒ |a - b| is even and |b - c| is even
⇒ (a - b) is even and (b - c) is even
⇒ (a - c) = (a - b) + (b - c) is even [Sum of two even integers is even]
⇒ |a - b| is even
⇒ (a, c) ∈ R
∴ R is transitive.
Hence, R is an equivalence relation.
Now, all elements of the set {1, 2, 3} are related to each other as all the elements of this subset are odd. Thus, the modulus of the difference between any two elements will be even.
Similarly, all elements of the set {2, 4} are related to each other as all the elements of this subset are even.
Also, no element of the subset {1, 3, 5} can be related to any element of {2, 4} as all elements of {1, 3, 5} are odd and all elements of {2, 4} are even. Thus, the modulus of the difference between the two elements (from each of these two subsets) will not be even. [as 1 – 2, 1 – 4, 3 – 2, 3 – 4, 5 – 2 and 5 – 4 all are odd].
Q9: Show that each of the relation R in the set A = {x ∈ Z : 0 ≤ x ≤ 12}, given by:
(i) R = {(a, b): |a – b| is a multiple of 4}
(ii) R = {(a, b): a = b}
is an equivalence relation. Find the set of all elements related to 1 in each case.
Ans: A = {x ∈ Z: 0 ≤ x ≤ 12}, = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
(i) R = {(a, b): |a – b| is a multiple of 4}
For any element a ∈ A, we have (a, a) ∈ R as |a – a| = 0 is a multiple of 4.
∴ R is reflexive.
Now, let (a, b) ∈ R ⇒ |a – b| is a multiple of 4.
⇒ |– (a – b)| = |b – a| is a multiple of 4.
⇒ (b, a) ∈ R
∴ R is symmetric.
Now, let (a, b), (b, c) ∈ R.
⇒ |a – b| is a multiple of 4 and |b – c| is a multiple of 4.
⇒ (a – b) is a multiple of 4 and (b – c) is a multiple of 4.
⇒ (a – c) = (a – b) + (b – c) is a multiple of 4.
⇒ |a – c| is a multiple of 4.
⇒ (a, c) ∈ R
∴ R is transitive.
Hence, R is an equivalence relation.
The set of elements related to 1 is {1, 5, 9} as
|1 – 1| = 0 is a multiple of 4.
|5 – 1| = 4 is a multiple of 4.
|9 – 1| = 8 is a multiple of 4.
(ii) R = {(a, b): a = b}
For any element a ∈ A, we have (a, a) ∈ R, since a = a.
∴ R is reflexive.
Now, let (a, b) ∈ R.
⇒ a = b
⇒ b = a ⇒ (b, a) ∈ R
∴ R is symmetric.
Now, let (a, b) ∈ R and (b, c) ∈ R.
⇒ a = b and b = c
⇒ a = c
⇒ (a, c) ∈ R
∴ R is transitive.
Hence, R is an equivalence relation.
The elements in R that are related to 1 will be those elements from set A which are equal to 1.
Hence, the set of elements related to 1 is {1}.
Q10: Given an example of a relation. Which is
(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.
Ans: (i) Let A = {5, 6, 7}.
Define a relation R on A as R = {(5, 6), (6, 5)}.
Relation R is not reflexive as (5, 5), (6, 6), (7, 7) ∉ R.
Now, as (5, 6) ∈ R and also (6, 5) ∈ R, R is symmetric.
⇒ (5, 6), (6, 5) ∈ R, but (5, 5) ∉ R
∴ R is not transitive.
Hence, relation R is symmetric but not reflexive or transitive.
(ii) Consider a relation R in R defined as:
R = {(a, b): a < b}
For any a ∈ R, we have (a, a) ∉ R since a cannot be strictly less than a itself.
In fact, a = a.
∴ R is not reflexive.
Now, (1, 2) ∈ R (as 1 < 2)
But, 2 is not less than 1.
∴ (2, 1) ∉ R
∴ R is not symmetric.
Now, let (a, b), (b, c) ∈ R.
⇒ a < b and b < c
⇒ a < c
⇒ (a, c) ∈ R
∴ R is transitive.
Hence, relation R is transitive but not reflexive and symmetric.
(iii) Let A = {4, 6, 8}.
Define a relation R on A as
A = {(4, 4), (6, 6), (8, 8), (4, 6), (6, 4), (6, 8), (8, 6)}
Relation R is reflexive since for every a ∈ A, (a, a) ∈ R
i.e., {(4, 4), (6, 6), (8, 8)} ∈ R.
Relation R is symmetric since (a, b) ∈ R ⇒ (b, a) ∈ R for all a, b ∈ R.
Relation R is not transitive since (4, 6), (6, 8) ∈ R, but (4, 8) ∉ R.
Hence, relation R is reflexive and symmetric but not transitive.
(iv) Define a relation R in R as:
R = {a, b) : a3 ≥ b3}
Clearly (a, a) ∈ R [ as a3 = a3]
∴ R is reflexive.
Now, (2, 1) ∈ R [as 23 ≥ 13]
But, (1, 2) ∉ R [as 13 < 23]
∴ R is not symmetric.
Now, Let (a, b), (b, c) ∈ R.
⇒ a3 ≥ b3 and b3 ≥ c3
⇒ a3 ≥ c3
⇒ (a, c) ∈ R
∴ R is transitive.
Hence, relation R is reflexive and transitive but not symmetric.
(v) Let A = {−5, −6}.
Define a relation R on A as
R = {(−5, −6), (−6, −5), (−5, −5)}
Relation R is not reflexive as (−6, −6) ∉ R.
Relation R is symmetric as (−5, −6) ∈ R and (−6, −5) ∈ R.
It is seen that (−5, −6), (−6, −5) ∈ R. Also, (−5, −5) ∈ R.
∴ The relation R is transitive.
Hence, relation R is symmetric and transitive but not reflexive.
Q11: Show that the relation R in the set A of points in a plane given by R = {(P, Q): Distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all point related to a point P ≠ (0, 0) is the circle passing through P with origin as centre.
Ans: R = {(P, Q): Distance of point P from the origin is the same as the distance of point Q from the origin}
Clearly, (P, P) ∈ R since the distance of point P from the origin is always the same as the distance of the same point P from the origin.
∴ R is reflexive.
Now, Let (P, Q) ∈ R.
⇒ The distance of point P from the origin is the same as the distance of point Q from the origin.
⇒ The distance of point Q from the origin is the same as the distance of point P from the origin.
⇒ (Q, P) ∈ R
∴ R is symmetric.
Now, Let (P, Q), (Q, S) ∈ R.
⇒ The distance of points P and Q from the origin is the same and also, the distance of points Q and S from the origin is the same.
⇒ The distance of points P and S from the origin is the same.
⇒ (P, S) ∈ R
∴ R is transitive.
Therefore, R is an equivalence relation.
The set of all points related to P ≠ (0, 0) will be those points whose distance from the origin is the same as the distance of point P from the origin.
In other words, if O (0, 0) is the origin and OP = k, then the set of all points related to P is at a distance of k from the origin.
Hence, this set of points forms a circle with the centre as the origin and this circle passes through point P.
Q12: Show that the relation R defined in the set A of all triangles as R = {(T1, T2) : T1 is similar to T2}, is equivalence relation. Consider three right angle triangles T1 with sides 3, 4, 5, T2 with sides 5, 12, 13 and T3 with sides 6, 8, 10. Which triangles among T1, T2 and T3 are related?
Ans: R = {(T1, T2): T1 is similar to T2}
R is reflexive since every triangle is similar to itself.
Further,
If (T1, T2) ∈ R, Then T1 is similar to T2}
⇒ T2 is similar to T1
⇒ (T2,T1) ∈ T
∴ R is symmetric.
Now,
Let (T1, T2), (T2, T3) ∈ R.
⇒ T1 is similar to T2 and T2 is similar to T3
⇒ T1 is similar to T3
⇒ (T1, T3) ∈ R
∴ R is transistive
Thus, R is an equivalent relation.
Now,
We can observe that
3/6 = 4/8 = 5/10 = 1/2
∴ The corresponding sides of triangles T1 and T3 are in the same ratio.
Then, triangle T1 is similar to T3
Hence, T1 is related to T3
Q13: Show that the relation R defined in the set A of all polygons as R = {(P1, P2): P1 and P2 have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right angle triangle T with sides 3, 4 and 5?
Ans: R = {(P1, P2) : P1 and P2 have same the number of sides}
R is reflexive,
Since (P1, P2) ∈ R, as the same polygon has the same number of sides with itself.
Let (P1, P2) ∈ R
⇒ P1 and P2 have the same number of sides.
⇒ P2 and P1 have the same number of sides.
⇒ (P1, P2)∈R
∴ R is symmetric
Now,
Let (P1, P2),(P2, P3) ∈ R
⇒ P1 and P2 have the same number of sides
Also, P2 and P3 have the same number of sides.
⇒ P1 and P3 have the same number of sides
⇒ (P1,P3) ∈ R
∴ R is transitive.
Hence, R is an equivalence relation.
The elements in A related to the right-angled triangle (T) with sides 3, 4, and 5 are those polygons which have 3 sides (Since T is a polygon with 3 sides).
Hence, the set of all elements in A related to triangle T is the set of all triangles.
Q14: Let L be the set of all lines in XY plane and R be the relation in L defined as R = {(L1, L2): L1 is parallel to L2}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.
Ans: R = {(L1, L2): L1 is parallel to L2}
R is reflexive as any line L1 is parallel to itself i.e., (L1, L2) ∈ R
Now, Let (L1, L2) ∈ R
⇒ L1 is parallel to L2
⇒ L2 is parallel to L1
⇒ (L2, L1) ∈ R
∴ R is symmetric
Now, Let (L1, L2), (L2, L3) ∈ R
⇒ L1 is parallel to L2. Also, L2 is parallel to L3
⇒ L1 is Parallel to L3
∴ R is transitive.
Hence, R is an equivalence relation.
The set of all lines related to the line y = 2x + 4 is the set of all lines that are parallel to the line y = 2x + 4.
Slope of line y = 2x + 4 is m = 2.
It is known that parallel lines have the same slopes.
The line parallel to the given line is of the form y = 2x + c, where c ∈ R.
Hence, the set of all lines related to the given line is given by y = 2x + c, where c ∈ R.
Q15: Let R be the relation in the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}.
Choose the correct answer.
(a) R is reflexive and symmetric but not transitive.
(b) R is reflexive and transitive but not symmetric.
(c) R is symmetric and transitive but not reflexive.
(d) R is an equivalence relation.
Ans: (b)
Solution: R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}
It is seen that (a, a) ∈ R, for every a ∈ {1, 2, 3, 4}.
∴ R is reflexive.
It is seen that (1, 2) ∈ R, but (2, 1) ∉ R.
∴ R is not symmetric.
Also, it is observed that (a, b), (b, c) ∈ R ⇒ (a, c) ∈ R for all a, b, c ∈ {1, 2, 3, 4}.
∴ R is transitive.
Hence, R is reflexive and transitive but not symmetric.
Q16: Let R be the relation in the set N given by R = {(a, b): a = b − 2, b > 6}.
Choose the correct answer.
(a) (2, 4) ∈ R
(b) (3, 8) ∈ R
(c) (6, 8) ∈ R
(d) (8, 7) ∈ R
Ans: (c)
Solution: R = {(a, b): a = b − 2, b > 6}
Now,
Since b > 6, (2, 4) ∉ R
Also, as 3 ≠ 8 − 2,
∴ (3, 8) ∉ R
And, as 8 ≠ 7 − 2
∴ (8, 7) ∉ R
Now, consider (6, 8).
We have 8 > 6 and also, 6 = 8 − 2.
∴ (6, 8) ∈ R
Exercise 1.2
Q1: Show that the function f: R∗ → R∗ defined by f(x) = 1/x is one-one and onto, where R∗ is the set of all non-zero real numbers. Is the result true, if the domain R∗ is replaced by N with co-domain being same as R∗?
Ans: It is given that f: R∗ → R∗ is defined by f(x)= 1/x
For one – one:
Let x, y ∈ R∗ such that f(x) = f(y)
⇒ 1/x = 1/y
⇒ x = y
∴ f is one – one.
For onto:
It is clear that for y ∈ R∗, there exists x= 1/y ∈ R∗ [as y ≠ 0] such that
Thus, the given function f is one – one and onto.
Now, consider function g: N → R∗ defined by g(x)= 1/x
We have,
g(x1) = g(x2)
⇒ 1/x1 = 1/x2 ⇒ x1 = x2
∴ g is one – one.
Further, it is clear that g is not onto as for 1.2 ∈ R∗ there does not exit any x in N such that g(x)=1/1.2.
Hence, function g is one-one but not onto.
Q2: Check the injectivity and surjectivity of the following functions:
(i) f : N → N given by f(x) = x2
(ii) f : Z → Z given by f(x) = x2
(iii) f : R → R given by f(x) = x2
(iv) f : N → N given by f(x) = x3
(v) f : Z → Z given by f(x) = x3
Ans: (i) f: N → N is given by f(x) = x2
It is seen that for x, y ∈ N, f(x) = f(y) ⇒ x2 = y2 ⇒ x = y.
∴ f is injective.
Now, 2 ∈ N. But, there does not exist any x in N such that f(x) = x2 = 2.
∴ f is not surjective.
Hence, function f is injective but not surjective.
(ii) f: Z → Z is given by f(x) = x2
It is seen that f(−1) = f(1) = 1, but −1 ≠ 1.
∴ f is not injective.
Now, −2 ∈ Z. But, there does not exist any element x ∈ Z such that
f(x) = −2 or x2 = −2.
∴ f is not surjective.
Hence, function f is neither injective nor surjective.
(iii) f: R → R is given by f(x) = x2
It is seen that f(−1) = f(1) = 1, but −1 ≠ 1.
∴ f is not injective.
Now, −2 ∈ R. But, there does not exist any element x ∈ R such that
f(x) = −2 or x2 = −2.
∴ f is not surjective.
Hence, function f is neither injective nor surjective.
(iv) f: N → N given by f(x) = x3
It is seen that for x, y ∈ N, f(x) = f(y) ⇒ x3 = y3 ⇒ x = y.
∴ f is injective.
Now, 2 ∈ N. But, there does not exist any element x ∈ N such that
f(x) = 2 or x3 = 2.
∴ f is not surjective
Hence, function f is injective but not surjective.
(v) f: Z → Z is given by f(x) = x3
It is seen that for x, y ∈ Z, f(x) = f(y) ⇒ x3 = y3 ⇒ x = y.
∴ f is injective.
Now, 2 ∈ Z. But, there does not exist any element x ∈ Z such that
f(x) = 2 or x3 = 2.
∴ f is not surjective.
Hence, function f is injective but not surjective.
Q3: Prove that the Greatest Integer Function f: R → R given by f(x) = [x], is neither one – one nor onto, where [x] denotes the greatest integer less than or equal to x.
Ans: f: R → R is given by, f(x) = [x]
It is seen that f(1.2) = [1.2] = 1, f(1.9) = [1.9] = 1.
∴ f(1.2) = f(1.9), but 1.2 ≠ 1.9.
∴ f is not one – one.
Now, consider 0.7 ∈ R.
It is known that f(x) = [x] is always an integer. Thus, there does not exist any element x ∈ R such that f(x) = 0.7.
∴ f is not onto.
Hence, the greatest integer function is neither one – one nor onto.
Q4: Show that the Modulus Function f: R → R given by f(x) = |x|, is neither one – one nor onto, where |x| is x, if x is positive or 0 and |x| is − x, if x is negative.
Ans:
It is clear that f(-1) = |-1| = 1 and f(1) = |1| = 1
∴ f(−1) = f(1), but −1 ≠ 1.
∴ f is not one – one. Now, consider −1 ∈ R.
It is known that f(x) = |x| is always non-negative. Thus, there does not exist any element x in domain R such that f(x) = |x| = −1.
∴ f is not onto.
Hence, the modulus function is neither one-one nor onto.
Q5: Show that the Signum Function f: R → R, given by
is neither one-one nor onto.
Ans:
It is seen that f(1) = f(2) = 1, but 1 ≠ 2.
∴ f is not one – one.
Now, as f(x) takes only 3 values (1, 0, or −1) for the element −2 in co-domain R, there does not exist any x in domain R such that f(x) = −2.
∴ f is not onto.
Hence, the Signum function is neither one – one nor onto.
Q6: Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one – one.
Ans: It is given that A = {1, 2, 3}, B = {4, 5, 6, 7}.
f: A → B is defined as f = {(1, 4), (2, 5), (3, 6)}.
∴ f (1) = 4, f (2) = 5, f (3) = 6
It is seen that the images of distinct elements of A under f are distinct.
Hence, function f is one – one.
Q7: In each of the following cases, state whether the function is one – one, onto or bijective. Justify your answer.
(i) f : R → R defined by f(x) = 3 − 4x
(ii) f : R → R defined by f(x) = 1 + x2
Ans: (i) f: R → R is defined as f(x) = 3 − 4x.
Let x1, x2 ∈ R such that f(x1) = f(x2)
⇒ 3 - 4x1 = 3 - 4x2 ⇒ -4x1 = -4x2
⇒ x1 = x2
∴ f is one – one.
For any real number (y) in R, there exists 3-y/4 in R such that
∴ f is onto.
Hence, f is bijective.
(ii) f : R → R is defined as f(x) = 1 + x2
Let x1, x2 ∈ R such that f (x1) = f(x2)
⇒ 1+ x12= 1+ x22⇒ x12 = x22
⇒ x1 = ± x2
∴ f(x1) = f(x2) does not imply that x1 = x2
For example, f(1)= f(-1)=2
∴ f is not one – one.
Consider an element −2 in co-domain R.
It is seen that f(x) = 1 + x2 is positive for all x ∈ R.
Thus, there does not exist any x in domain R such that f(x) = −2.
∴ f is not onto.
Hence, f is neither one – one nor onto.
Q8: Let A and B be sets. Show that f: A × B → B × A such that (a, b) = (b, a) is bijective function.
Ans: f : A × B → B × A is defined as f(a, b) = (b, a).
Let (a1, b1), (a2, b2) ∈ A × B such that f(a1, b1) = f(a2, b2)
⇒ (b1, a1) = (b2, a2)
⇒ b1 = b2 and a1 = a2
∴ f is one – one.
Now, let (b, a) ∈ B × A be any element.
Then, there exists (a, b) ∈ A × B such that f(a, b) = (b, a). [By definition of f]
∴ f is onto.
Hence, f is bijective.
Q9: Let f: N → N be defined by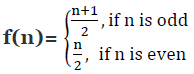
for all n ∈ N. State whether the function f is bijective. Justify your answer.
Ans: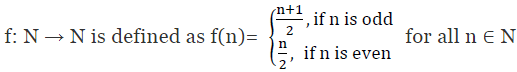
It can be observed that:
f(1) = 1 + 1/2 = 1 and f(2) = 2/2 = 1 [By definition of f(n)]
f(1) = f(2), where 1 ≠ 2
∴ f is not one-one.
Consider a natural number (n) in co-domain N.
Case I: n is odd
∴ n = 2r + 1 for some r ∈ N. Then, there exists 4r + 1∈ N such that f(4r + 1) = 4r + 1 + 1/2 = 2r + 1
Case II: n is even
∴ n = 2r for some r ∈ N. Then, there exists 4r ∈ N such that f(4r) = 4r/2 = 2r
∴ f is onto.
Hence, f is not a bijective function.
Q10: Let A = R − {3} and B = R − {1}. Consider the function f: A → B defined by (x) = (x-2/x-3). Is f one-one and onto? Justify your answer.
Ans:
A = R − {3}, B = R − {1} and f: A → B defined by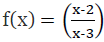
Let x, y ∈ A such that f(x) = f(y)
⇒ (x – 2)(y – 3) = (y – 2)(x – 3)
⇒ xy – 3x – 2y + 6 = xy – 2x – 3y + 6
⇒ – 3x – 2y = – 2x – 3y ⇒ x = y
∴ f is one-one.
Let y ∈ B = R − {1}. Then, y ≠ 1.
The function f is onto if there exists x ∈ A such that f(x) = y.
Now, f(x) = y
y = (x - 2/ x - 3)
⇒ x – 2 = xy – 3y ⇒ x(1 – y) = – 3y + 2
⇒ x=(2-3y )/(1-y) ∈A [y ≠ 1]
∴ f is onto.
Hence, function f is one – one and onto.
Q11: Let f: R → R be defined as f(x) = x4. Choose the correct answer.
(a) f is one-one onto
(b) f is many-one onto
(c) f is one-one but not onto
(d) f is neither one-one nor onto
Ans: (d)
Solution: f : R → R is defined as f(x) = x4.
Let x, y ∈ R such that f(x) = f(y).
⇒ x4 = y4
⇒ x = ± y
∴ f(x) = f(y) does not imply that x = y.
For example f(1) = f(–1) = 1
∴ f is not one-one.
Consider an element 2 in co-domain R. It is clear that there does not exist any x in domain R such that f(x) = 2.
∴ f is not onto.
Hence, function f is neither one – one nor onto.
Q12: Let f: R → R be defined as f(x) = 3x. Choose the correct answer.
(a) f is one – one and onto
(b) f is many – one and onto
(c) f is one – one but not onto
(d) f is neither one – one nor onto
Ans: (a)
Solution: f : R → R is defined as f(x) = 3x.
Let x, y ∈ R such that f(x) = f(y).
⇒ 3x = 3y
⇒ x = y
∴ f is one-one.
Also, for any real number(y) in co-domain R, there exists y/3 in R such that f(y/3) = 3(y/3) = y
∴ f is onto.
Hence, function f is one – one and onto.
|
223 videos|377 docs|167 tests
|
FAQs on NCERT Solutions Class 11 Maths Chapter 2 - Relations and Functions
| 1. What are relations and functions in mathematics? |  |
| 2. How do you determine if a relation is a function? |  |
| 3. What are the different types of functions? |  |
| 4. How do you find the domain and range of a function? |  |
| 5. How are relations and functions used in real-life applications? |  |

















