NCERT Solutions Class 12 Maths Chapter 4 - Determinants

Q1: Examine the consistency of the system of equations.
 x + 2y = 2
 2x + 3y = 3
Ans: The given system of equations is:
x + 2y = 2
2x + 3y = 3
The given system of equations can be written in the form of AX = B, where

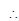 A is non-singular.
Therefore, A⁻¹ exists.
Hence, the given system of equations is consistent.

Q2: Examine the consistency of the system of equations.
2x − y = 5 x
x + y = 4
Ans: The given system of equations is:
2x − y = 5 x
+ y = 4
The given system of equations can be written in the form of AX = B, where

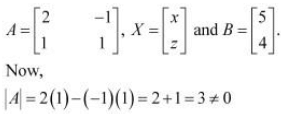
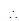 A is non-singular.
Therefore, A⁻¹ exists.
Hence, the given system of equations is consistent.

Q3: Examine the consistency of the system of equations.
x + 3y = 5
2x + 6y = 8
Ans: The given system of equations is:
x + 3y = 5
2x + 6y = 8
The given system of equations can be written in the form of AX = B, where

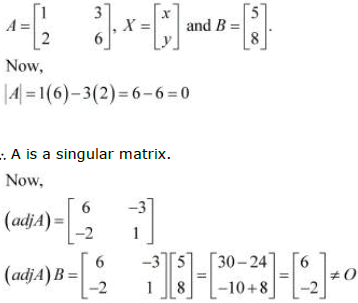
Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.

Q4: Examine the consistency of the system of equations.
x + y + z = 1 
2x + 3y + 2z = 2 
ax + ay + 2az = 4
Ans: The given system of equations is:
x + y + z = 1 2x
+ 3y + 2z = 2 ax
+ ay + 2az = 4
This system of equations can be written in the form AX = B, where

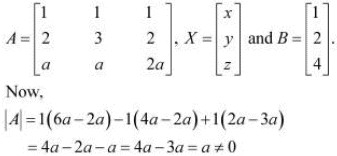
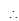 A is non-singular.
Therefore, A⁻¹ exists.
Hence, the given system of equations is consistent.

Q5: Examine the consistency of the system of equations.
3x − y − 2z = 2
2y − z = −1
3x − 5y = 3
Ans: The given system of equations is:
3x − y − 2z = 2
2y − z = −1
3x − 5y = 3
This system of equations can be written in the form of AX = B, where

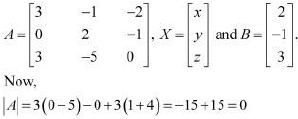
A is a singular matrix.



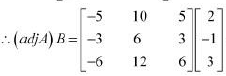
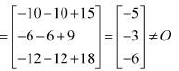
Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.

Q6: Examine the consistency of the system of equations.
5x − y + 4z = 5
2x + 3y + 5z = 2
5x − 2y + 6z = −1
Ans: The given system of equations is:
5x − y + 4z = 5
2x + 3y + 5z = 2
5x − 2y + 6z = −1
This system of equations can be written in the form of AX = B, where

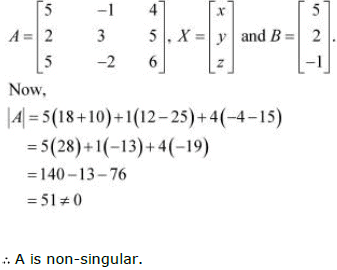
Therefore, A⁻¹ exists.
Hence, the given system of equations is consistent.

Q7: Solve system of linear equations, using matrix method.

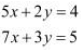
Ans: The given system of equations can be written in the form of AX = B, where

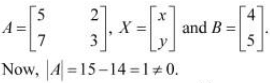
Thus, A is non-singular. Therefore, its inverse exists.


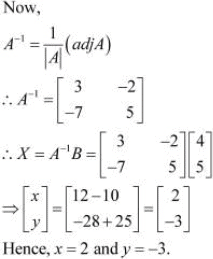
Q8: Solve system of linear equations, using matrix method.

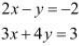
Ans: The given system of equations can be written in the form of AX = B, where

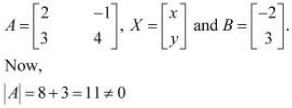
Thus, A is non-singular. Therefore, its inverse exists.


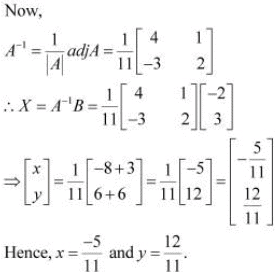
Q9: Solve system of linear equations, using matrix method.

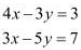
Ans: The given system of equations can be written in the form of AX = B, where

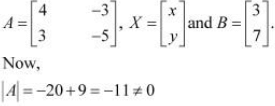
Thus, A is non-singular. Therefore, its inverse exists.





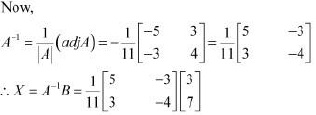
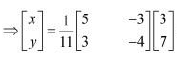
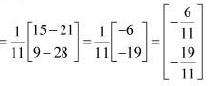
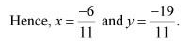
Q10: Solve system of linear equations, using matrix method.
5x + 2y = 3
3x + 2y = 5
Ans: The given system of equations can be written in the form of AX = B, where

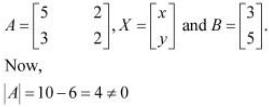
Thus, A is non-singular. Therefore, its inverse exists.

Q11: Solve system of linear equations, using matrix method.

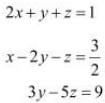
Ans: The given system of equations can be written in the form of AX = B, where

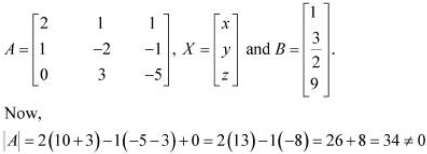
Thus, A is non-singular. Therefore, its inverse exists.


Q12: Solve system of linear equations, using matrix method.
x − y + z = 4 
2x + y − 3z = 0 
x + y + z = 2
Ans: The given system of equations can be written in the form of AX = B, where

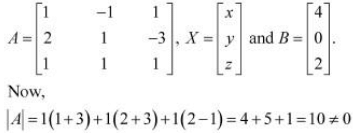
Thus, A is non-singular. Therefore, its inverse exists.


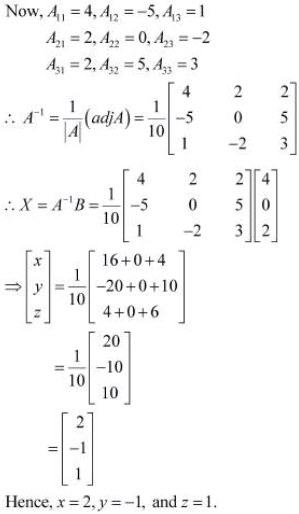
Q13: Solve system of linear equations, using matrix method.
2x + 3y + 3z = 5
x − 2y + z = −4
3x − y − 2z = 3
Ans: The given system of equations can be written in the form AX = B, where

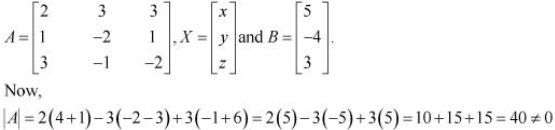
Thus, A is non-singular. Therefore, its inverse exists.


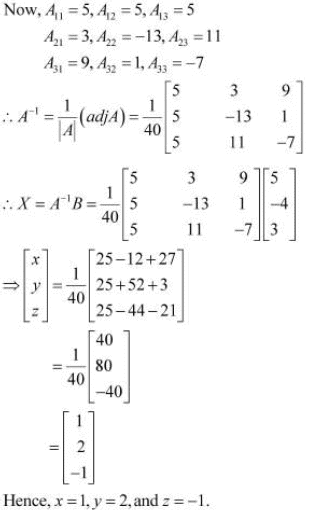
Q14: Solve system of linear equations, using matrix method.
x − y + 2z = 7
3x + 4y − 5z = −5
2x − y + 3z = 12
Ans: The given system of equations can be written in the form of AX = B, where

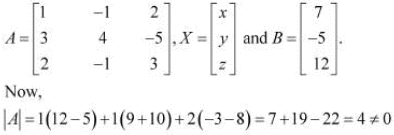
Thus, A is non-singular. Therefore, its inverse exists.


Q15: If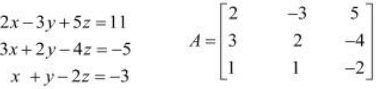   
find A⁻¹. Using A⁻¹ solve the system of equations
Ans: 

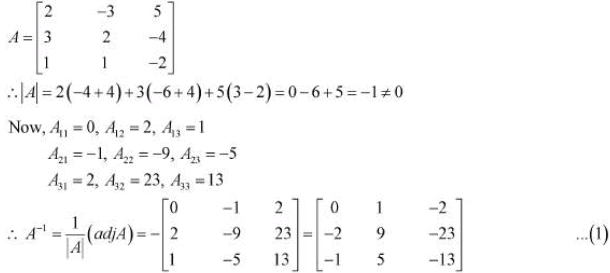
Now, the given system of equations can be written in the form of AX = B, where



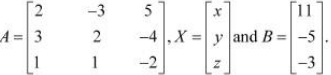
Q16: The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs 90. The cost of 6 kg onion 2 kg wheat and 3 kg rice is Rs 70. Find cost of each item per kg by matrix method.
Ans: Let the cost of onions, wheat, and rice per kg be Rs x, Rs y,and Rs z respectively.
Then, the given situation can be represented by a system of equations as:

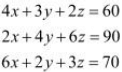
This system of equations can be written in the form of AX = B, where

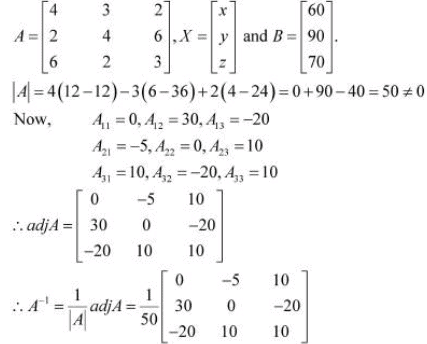
Now,
X = A⁻¹ B

Hence, the cost of onions is Rs 5 per kg, the cost of wheat is Rs 8 per kg, and the cost of rice is Rs 8 per kg.