Question 1:
Verify Rolle’s Theorem for the function 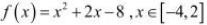
Answer
The given function, 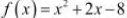 , being a polynomial function, is continuous in [−4,2] and is differentiable in (−4, 2).
, being a polynomial function, is continuous in [−4,2] and is differentiable in (−4, 2).
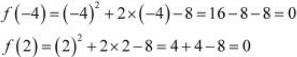
∴ f (−4) = f (2) = 0
⇒ The value of f (x) at −4 and 2 coincides.
Rolle’s Theorem states that there is a point c ∈ (−4, 2) such that 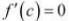
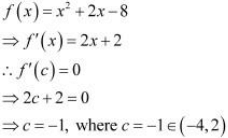
Hence, Rolle’s Theorem is verified for the given function.
Question 2:
Examine if Rolle’s Theorem is applicable to any of the following functions. Can you say
some thing about the converse of Rolle’s Theorem from these examples?
(i) 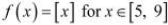
(ii) 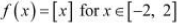
(iii) 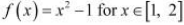
Answer
By Rolle’s Theorem, for a function 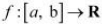 , if
, if
(a) f is continuous on [a, b]
(b) f is differentiable on (a, b)
f (a) = f (b)
then, there exists some c ∈ (a, b) such that 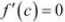
Therefore, Rolle’s Theorem is not applicable to those functions that do not satisfy any of
the three conditions of the hypothesis.

Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴ f is not differentiable in (5, 9).
It is observed that f does not satisfy all the conditions of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for 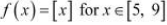 .
.
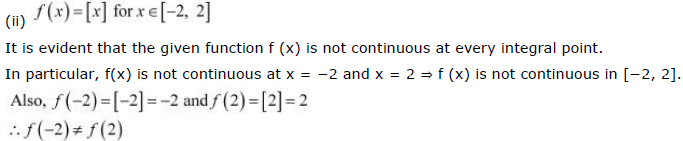
The differentiability of f in (−2, 2) is checked as follows.
Let n be an integer such that n ∈ (−2, 2).
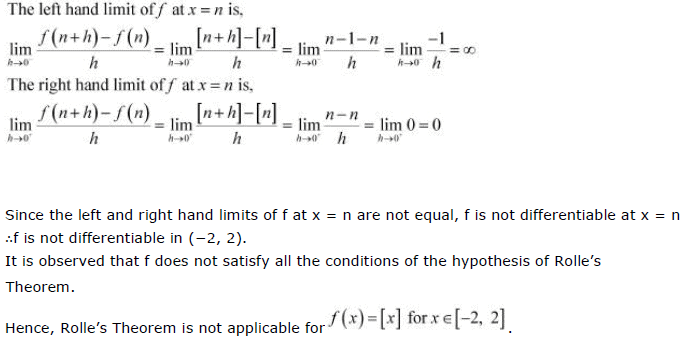

Question 3:
If 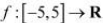 is a differentiable function and if
is a differentiable function and if 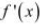 does not vanish anywhere,
does not vanish anywhere,
then prove that 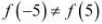
Answer
It is given that 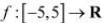 is a differentiable function.
is a differentiable function.
Since every differentiable function is a continuous function, we obtain
(a) f is continuous on [−5, 5].
(b) f is differentiable on (−5, 5).
Therefore, by the Mean Value Theorem, there exists c ∈ (−5, 5) such that
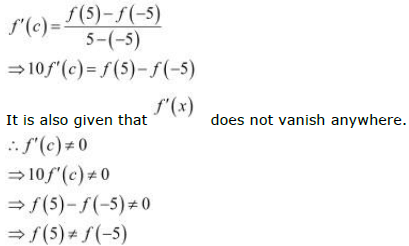
Hence, proved.
Question 4:
Verify Mean Value Theorem, if 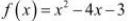 in the interval [a, b], where a =1 and b = 3.
in the interval [a, b], where a =1 and b = 3.
Answer
The given function is 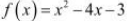
f, being a polynomial function, is continuous in [1, 4] and is differentiable in (1, 4) whose derivative is 2x − 4.
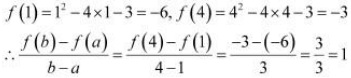
Mean Value Theorem states that there is a point c (1, 4) such that 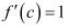
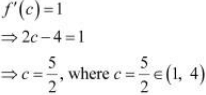
Hence, Mean Value Theorem is verified for the given function.
Question 5:
Verify Mean Value Theorem , if  in the interval [a, b], where a =1
in the interval [a, b], where a =1
 b=3
b=3
Find all c
Answer
The given function f is 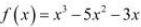
f, being a polynomial function, is continuous in [1, 3] and is differentiable in (1, 3)
whose derivative is 3x2 − 10x − 3.
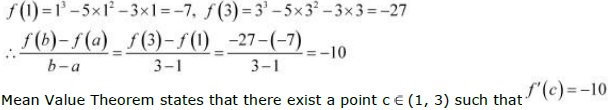
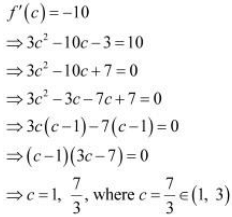
Hence, Mean Value Theorem is verified for the given function and 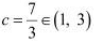 is the
is the
only point for which 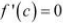
Question 6:
Examine the applicability of Mean Value Theorem for all three functions given in the above exercise 2.
Answer
Mean Value Theorem states that for a function 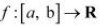 , if
, if
(a) f is continuous on [a, b]
(b) f is differentiable on (a, b)
then, there exists some c ∈ (a, b) such that 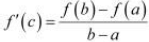
Therefore, Mean Value Theorem is not applicable to those functions that do not satisfy
any of the two conditions of the hypothesis.
(i) 
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = 5 and x = 9 ⇒ f (x) is not continuous in [5, 9].
The differentiability of f in (5, 9) is checked as follows.
Let n be an integer such that n ∈ (5, 9).
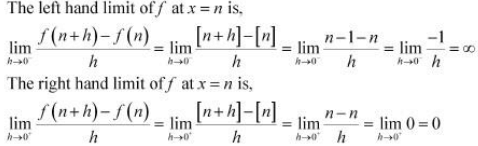
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴ f is not differentiable in (5, 9).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for 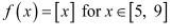 .
.
(ii) 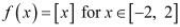
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = −2 and x = 2 ⇒ f (x) is not continuous in [−2, 2].
The differentiability of f in (−2, 2) is checked as follows.
Let n be an integer such that n ∈ (−2, 2).
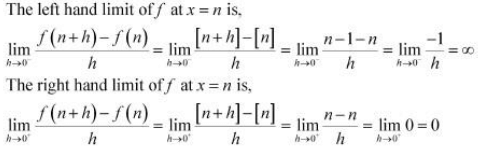
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴ f is not differentiable in (−2, 2).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for 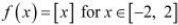 .
.
(iii) 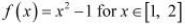
It is evident that f, being a polynomial function, is continuous in [1, 2] and is differentiable in (1, 2).
It is observed that f satisfies all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is applicable for 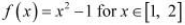 .
.
It can be proved as follows.
FAQs on Continuity & Differentiability, NCERT Solutions, Class 12, Maths , Part -8 - JEE
| 1. What is the concept of continuity in mathematics? |  |
| 2. How is the continuity of a function defined mathematically? |  |
| 3. What is the significance of continuity in real-world applications? |  |
| 4. What is the difference between continuity and differentiability? |  |
| 5. How can we determine the differentiability of a function? |  |


















