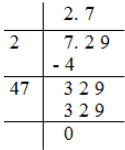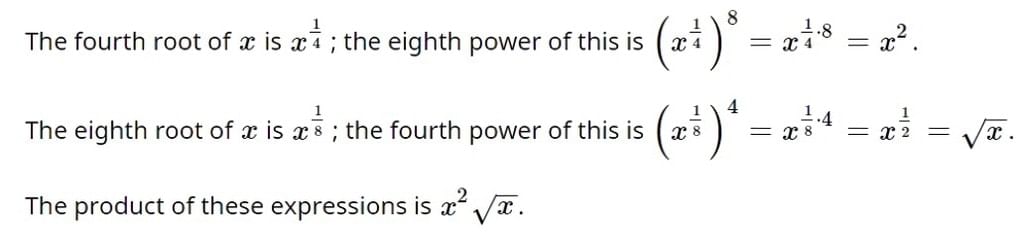Overview: Squares and Square Roots | CSAT Preparation - UPSC PDF Download
| Table of contents |

|
| Square Numbers |

|
| Properties of Square Numbers |

|
| Square Root |

|
| How to Find the Square Root of an Integer? |

|
| Important Points to Remember: |

|
| Solved Questions on Squaring and Square Roots |

|
Square Numbers
When a number or integer (not a fraction) is multiplied by itself, the resultant is called a ‘Square Number’.
- Any natural number ‘p’ which can be represented as y2, where y is a natural number, then ‘p’ is called a Square Number.
Example
4 = 22
9 = 32
16 = 42Where 2, 3, 4 are the natural numbers and 4, 9, 16 are the respective square numbers. Such types of numbers are also known as Perfect Squares.
- For example, 3 multiplied by 3 is equal to 3-squared or 3 x 3 = 32. So, basically, the exponential form of multiplication of a number or integer by itself is called a square number.
- Square numbers are always positive. If the negative sign is multiplied by itself, it results in a positive sign (+). For example, (-4)2 = 16. So, we can say here 16 is a positive square number, whose square root is an integer again, i.e.√16 = 4.
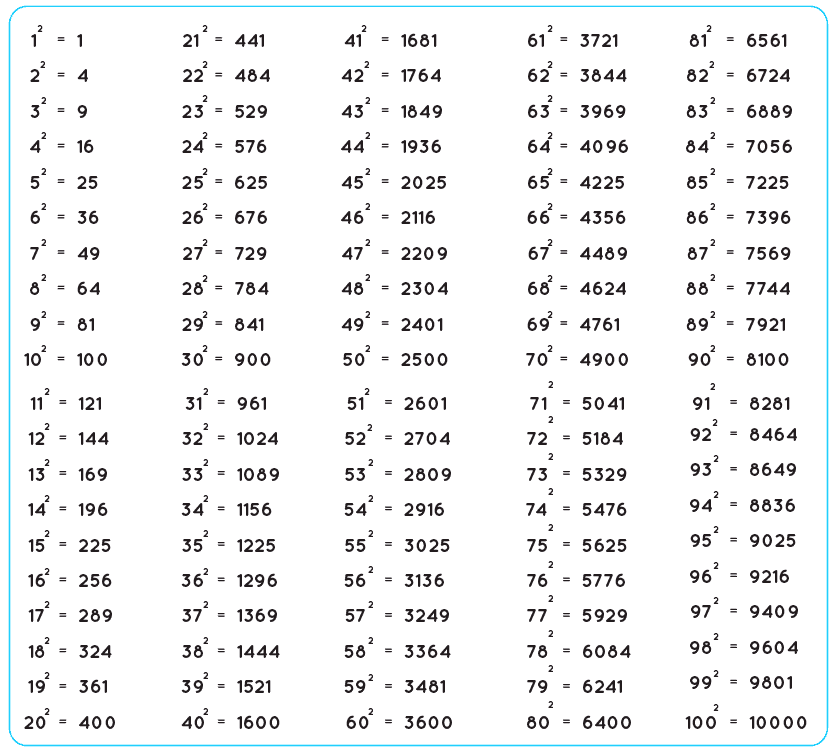
- Numbers such as 1, 4, 9, 16, 25, 36, 49, 64, etc. are special numbers as these are the product of a number by itself.
- If we express a number (x) in terms of the square of any natural number such as a2, then x is a square number.
- For example, 100 can be expressed as 10 × 10 = 102, where 10 is a natural number, therefore 100 is a square number.
- Whereas, the number 45 cannot be called a square number because it is the product of numbers 9 and 5. The number is not multiplied by itself. Square numbers can also be called perfect square numbers.
List of Square Numbers
Odd and Even Square Numbers
- Squares of even numbers are even, i.e, (2n)2 = 4n2.
- Squares of odd numbers are odd, i.e, (2n + 1) = 4(n2 + n) + 1.
- Since every odd square is of the form 4n + 1, the odd numbers that are of the form 4n+3 are not square numbers.
Properties of Square Numbers
The following are the properties of the square numbers:
- A number with 2, 3, 7 or 8 at the unit’s place should never be a perfect square. In other words, none of the square numbers ends in 2, 3, 7 or 8.
- If the number of zeros at the end is even, then the number is a perfect square number. Otherwise, we can say that a number ending in an odd number of zeros is never a perfect square.
- If the even numbers are squared, it always gives even numbers. Also, if the odd numbers are squared, it always gives odd numbers.
- If the natural numbers other than one are squared, it should be either a multiple of 3 or exceeds a multiple of 3 by 1.
- If the natural numbers other than one is squared, it should be either a multiple of 4 or exceeds a multiple of 4 by 1.
- It is noted that the unit’s digit of the square of a natural number is equal to the unit’s digit of the square of the digit at unit’s place of the given natural number.
- There are n natural numbers, say p and q such that p 2 = 2q 2
- For every natural number n, we can write it as: (n + 1)2 – n 2 = ( n + 1) + n..
- If a number n is squared, it equals the sum of the first n odd natural numbers.
- For any natural number, say”n” which is greater than 1, we can say that (2n, n 2 – 1, n 2 + 1) should be a Pythagorean triplet.
- Any number having 1 or 9 in its one’s place will always have a square ending with 1.
- Any number which has 4 or 6 in its unit’s place, its square will always end with 6.
- Any number which has 0 in its unit’s place, its square will always have an even number of zeros at the end.
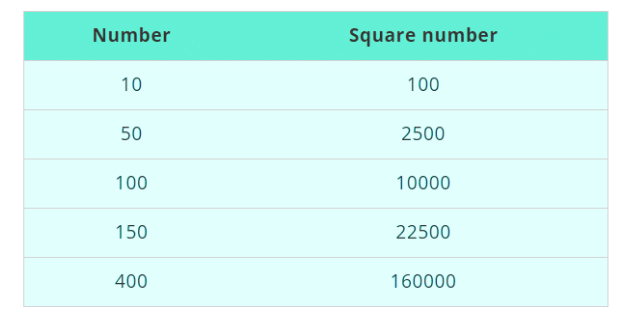
Finding the Square of a Number
To find the square of any number we needed to divide the number into two parts then we can solve it easily.If number is ‘x’ then x = (p + q) and x2 = (p + q)2You can also use the formula (p + q)2 = p2 + 2pq + q2Example: Find the square of 53.
Solution: Divide the number in two parts.53 = 50 + 3
532 = (50 + 3)2
= (50 + 3) (50 + 3)
= 50(50 + 3) +3(50 + 3)
= 2500 + 150 + 150 + 9
= 2809
1. Other pattern for the number ending with 5
For numbers ending with 5 we can use the pattern
(a5)2 = a × (a + 1)100 + 25
Example
252= 625 = (2 × 3) 100 + 25452 = 2025 = (4 × 5) 100 + 25
952 = 9025 = (9 × 10) 100 + 25
1252 = 15625 = (12 × 13) 100 + 25
2. Pythagorean TripletsIf the sum of two square numbers is also a square number, then these three numbers form a Pythagorean triplet.For any natural number p >1, we have (2p) 2 + (p2 -1)2 = (p2 + 1)2. So, 2p, p2-1 and p2+1 forms a Pythagorean triplet.
Example: Write a Pythagorean triplet having 22 as one its members.
Solution:
Let 2p = 6
P = 3
p2 + 1 = 10
p2 - 1 = 8.
Thus, the Pythagorean triplet is 6, 8 and 10.
62 + 82 = 102
36 + 64 = 100
Square Root
When you square a number, you are multiplying it by itself, e.g. 6*6 = 36. When you take the square-root of a number, you are undoing the square, going backwards from the result of squaring to the input that was originally squared: √ 36 = 6. Similarly, 8*8 = 64, so √ 64 = 8. As long as all the numbers are positive, everything is straightforward.
The process of finding the square root is called evaluation. The square root of a number is denoted by the symbol called the radical sign(√ ).
Symbol of Positive Square Root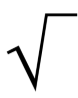
How to Find the Square Root of an Integer?
(i) By the method of Prime Factors:
When a given number is a perfect square, we resolve it into prime factors and take the product of prime factors, choosing one out of every two.
To find the square root of a perfect square by using the prime factorization method when a given number is a perfect square:
- Step I: Resolve the given number into prime factors.
- Step II: Make pairs of similar factors.
- Step III: Take the product of prime factors, choosing one factor out of every pair.
Examples on square root of a perfect square by using the prime factorization method:
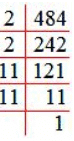
Example 1: Find the square root of 484 by prime factorization method.
Solution:
Resolving 484 as the product of primes, we get
484 = 2 × 2 × 11 × 11
√484 = √(2 × 2 × 11 × 11)
= 2 × 11
Therefore, √484 = 22
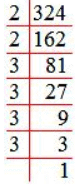
Example 2: Find the square root of 324.
Solution: The square root of 324 by prime factorization, we get
324 = 2 × 2 × 3 × 3 × 3 × 3
√324 = √(2 × 2 × 3 × 3 × 3 × 3)
= 2 × 3 × 3
Therefore, √324 = 18
(ii) By the method of Long Division:
This method can be used when the number is large and the factors cannot be determined easily. This method can also be used when we want to add a least number or to subtract a least number from a given number so that the resulting number may give a perfect square of some number.
Steps of Long Division Method for Finding Square Roots:
- Step I: Group the digits in pairs, starting with the digit in the units place. Each pair and the remaining digit (if any) is called a period.
- Step II: Think of the largest number whose square is equal to or just less than the first period. Take this number as the divisor and also as the quotient.
- Step III: Subtract the product of the divisor and the quotient from the first period and bring down the next period to the right of the remainder. This becomes the new dividend.
- Step IV: Now, the new divisor is obtained by taking two times the quotient and annexing with it a suitable digit which is also taken as the next digit of the quotient, chosen in such a way that the product of the new divisor and this digit is equal to or just less than the new dividend.
- Step V: Repeat steps (2), (3) and (4) till all the periods have been taken up. Now, the quotient so obtained is the required square root of the given number.
Examples on square root of a perfect square by using the long division method
Example 1: Find the square root of 784 by the long-division method.
Solution:
Marking periods and using the long-division method,
Therefore, √784 = 28
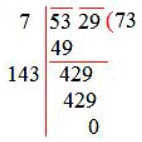
Example 2: Evaluate √5329 using the long-division method.
Solution: Marking periods and using the long-division method,
Therefore, √5329 =73
Properties of Squares:
- When a perfect square is written as a product of its prime factors each prime factor will appear an even number of times.
- The difference between the squares of two consecutive natural numbers is always equal to the sum of the natural numbers. Thus, 412 – 402 = (40 + 41) = 81.
This property is very useful when used in the opposite direction—i.e. Given that the difference between the squares of two consecutive integers is 81, you should immediately realise that the numbers should be 40 and 41. - The square of a number ending in 1, 5, or 6 also ends in 1, 5 or 6 respectively.
- The square of any number ending in 5: The last two digits will always be 25. The digits before that in the answer will be got by multiplying the digits leading up to the digit 5 in the number by 1 more than itself.
- Illustration:
852 = ___25.
The missing digits in the above answer will be got by 8 × (8 + 1) = 8 × 9 = 72. Hence, the square of 85 is given by 7225.
Similarly, 1352 = ___25. The missing digits are 13 × 14 = 182. Hence, 1352 = 18225. - The value of a perfect square has to end in 1, 4, 5, 6, 9 or an even number of zeros.
In other words, a perfect square cannot end in 2, 3, 7, or 8 or an odd number of zeros. - If the units digit of the square of a number is 1, then the number should end in 1 or 9.
- If the units digit of the square of a number is 4, then the units digit of the number is 2 or 8.
- If the units digit of the square of a number is 9, then the units digit of the number is 3 or 7.
- If the units of the square of a number is 6, then the unit’s digit of the number is 4 or 6.
- The sum of the squares of the first ‘n’ natural numbers is given by
[(n) (n + 1) (2n + 1)]/6. - Normally, by squaring any number we increase the value of the number. The only integers for which this is not true are 0 and 1. (In these cases squaring the number has no effect on the value of the number).
Further, for values between 0 to 1, squaring the number reduces the value of the number. For example 0.52 < 0.5.
Square Root
If x2 = y, we say that the square root of y is x and we write y = x.
Thus, √4 = 2, √9 = 3, √196 = 14.
Important Points to Remember:
1. 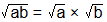
2. 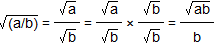
3. Number ending in 8 can never be a perfect square.
4. Remember the squares and cubes of 2 to 10. This will help in easily solving the problems.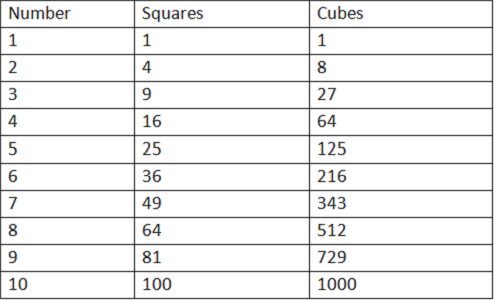
Square Roots of Decimals
To find the square root of a decimal number we have to put bars on the primary part of the number in the same manner as we did above. And for the digits on the right of the decimal we have to put bars starting from the first decimal place.
Rest of the method is same as above. We just need to put the decimal in between when the decimal will come in the division.
Example: Find √7.29 using the division method.
Solution:
Thus, √7.29 = 2.7
Remark: To put the bar on a number like 174.241, we will put a bar on 74 and a bar on 1 as it is a single digit left. And in the numbers after decimal, we will put a bar on 24 and put zero after 1 to make it double-digit.
174. 24 10
Estimating Square Root
Sometimes we have to estimate the square root of a number if it’s not possible to calculate the exact square root.
Example: Estimate the square root of 300.
Solution:We know that, 300 comes between 100 and 400 i.e. 100 < 300 < 400.
Now, √100 = 10 and √400 = 20.So, we can say that
10 < √300 < 20.
We can further estimate the numbers as we know that 172 = 289 and 182 = 324.
Thus, we can say that the square root of √300 = 17 as 289 is much closer to 300 than 324.
Solved Questions on Squaring and Square Roots
Q1: Simplify the following expression.
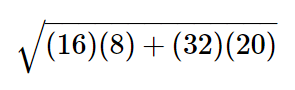
Solution:
Q2: Simplify the following expression.

Solution:
Q3: Assume x to be positive. Multiply the eighth power of the fourth root of x by the fourth power of the eighth root of x. What is the product?
Solution:
|
205 videos|264 docs|136 tests
|
FAQs on Overview: Squares and Square Roots - CSAT Preparation - UPSC
| 1. What are square numbers and how are they defined? |  |
| 2. What properties do square numbers possess? |  |
| 3. How can we find the square root of an integer? |  |
| 4. What are some important points to remember about squaring and square roots? |  |
| 5. Can you provide examples of solved questions on squaring and square roots? |  |