Circle, Ellipse, Parabola & Hyperbola: Solved Examples | General Test Preparation for CUET UG - CUET Commerce PDF Download
| Table of contents |

|
| The Standard Form of Circle |

|
| The Ellipse |

|
| The Parabola |

|
| The Hyperbola |

|
The Standard Form of Circle
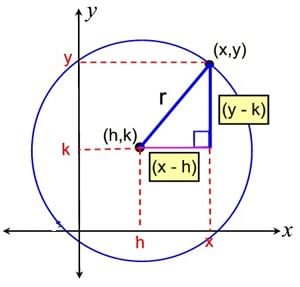
- (x - h)2 + (y - k)2 = r2
Where the center is (h, k) and radius is ‘r’. - If center of the circle is at the origin and the radius is 'r', then the equation of the circle is:
x2 + y2 = r2 - This is also known as the simplest form.
Example 1: If the area of the circle shown below is kπ, what is the value of k?
(a) 4
(b) 16
(c) 32
(d) 20
Correct Answer is Option (c)
Since the line segment joining (4, 4) and (0, 0) is a radius of the circle:
r2 = 42 + 42 = 32
Therefore, area = πr2 = 32π ⇒ k = 32
(x - 4)2 + (y - 3)2 = 25
The Ellipse
- Though not so simple as the circle, the ellipse is nevertheless the curve most often "seen" in everyday life. The reason is that every circle, viewed obliquely, appears elliptical.
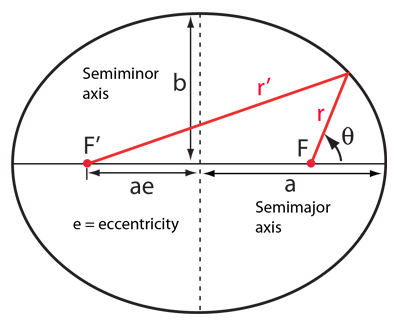 Ellipse
Ellipse - The equation of an ellipse centered at the origin and with an axial intersection at (±, a, 0) and (± b, 0) is:
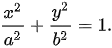
The Parabola
- When a baseball is hit into the air, it follows a parabolic path. There are all kinds of parabolas, and there’s no simple, general parabola formula for you to memorize.
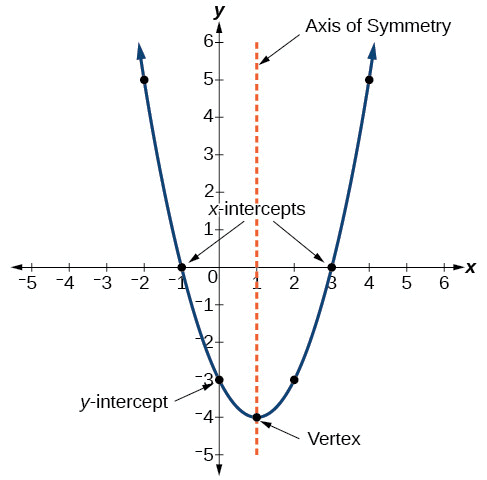 Parabola
Parabola - You should know, however, that the graph of the general quadratic equation:
y = ax2 + bx + c is a parabola. - It’s one that opens up either on top or on the bottom, with an axis of symmetry parallel to the y-axis. The graph of the general quadratic equation y = ax2 + bx + c is a parabola.
Examples: y = x2 - 2x + 1 and y = - x2 - 4 are examples of some parabolic equations.
The Hyperbola
- If a right circular cone is intersected by a plane parallel to its axis, part of a hyperbola is formed.
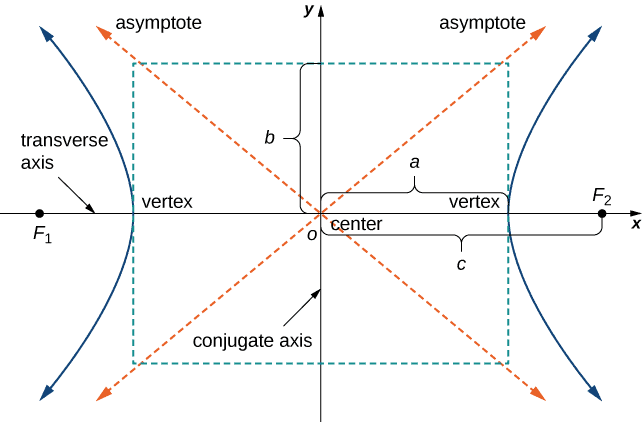 Hyperbola
Hyperbola - The equation of a hyperbola at the origin and with foci on the x-axis is:
Example 2: Find the area enclosed by the figure | x | + | y | = 4.
The four possible lines are:
x + y = 4; x - y = 4; - x - y = 4 and -x + y = 4
The four lines can be represented on the coordinates axes as shown in the figure. Thus a square is formed with the vertices as shown. The side of the square is:
The area of the square is= 32 sq. units.
Example 3: If point (t, 1) lies inside circle x2 + y2 = 10, then t must lie between:
As (t, 1) lies inside the circle, so its distance from centre i.e. origin should be less than radius i.e.
Example.4 Find the equation of line passing through (2, 4) and through the intersection of line 4x - 3y - 21 = 0 and 3x - y - 12 = 0?
4x - 3y - 21 = 0 …..(1)
3x - y - 12 = 0 ….(2)
Solving (1) and (2), we get point of intersection as x = 3 & y = - 3.
Now we have two points (3, -3) & (2, 4)
⇒ Slope of line m == - 7
So, the equation of line is:
⇒ y + 3 = - 7 (x - 3)
⇒ 7x + y - 18 = 0
Alternate Method:
Equation of line through intersection of 4x - 3y - 21 = 0 and 3x - y - 12 = 0 is:
(4x - 3y - 21) + k(3x - y - 12) = 0.
As this line passes through (2, 4):
⇒ (4 × 2 - 3 × 4 - 21) + k(3 × 2 - 4 - 12) = 0
⇒ k =
So, the equation of line is:
|
164 videos|626 docs|1131 tests
|
FAQs on Circle, Ellipse, Parabola & Hyperbola: Solved Examples - General Test Preparation for CUET UG - CUET Commerce
| 1. What is the standard form of a circle? |  |
| 2. How is an ellipse different from a circle? |  |
| 3. What is the equation of a parabola? |  |
| 4. How can you distinguish between a hyperbola and an ellipse? |  |
| 5. How can the standard form of each conic section be used in real-life applications? |  |
















