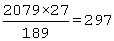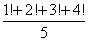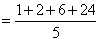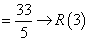Introduction: Number System | CSAT Preparation - UPSC PDF Download
- Numbers are the foundation of all mathematical reasoning and play a vital role in every aspect of our lives—from daily calculations to complex problem-solving.
- In this chapter, we embark on an important journey to explore the different types of numbers and the categories they fall under.
- This marks your first step towards mastering the number system, a key area in most entrance exams.
- As we progress, you'll find that many of these concepts are familiar from school, reinforcing your understanding and boosting your confidence to tackle advanced problems with ease.
What is a Number?
A number is a mathematical concept used for counting, measuring, or labelling things. Numbers play a key role in arithmetic calculations.
- They come in various types, including natural numbers, whole numbers, rational and irrational numbers. Even 0 is a number, representing a null value.
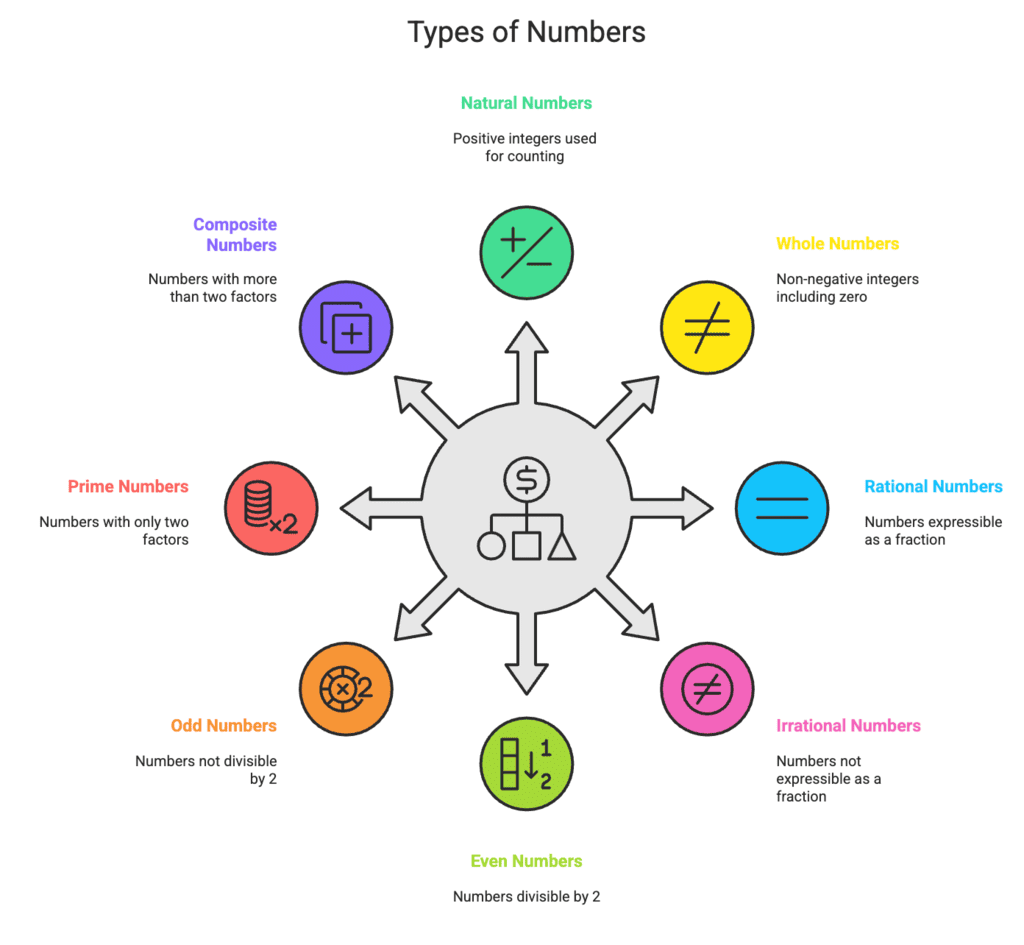
- Numbers can be classified as even or odd based on divisibility by 2, and as prime or composite depending on the number of factors. Even and odd refer to divisibility by 2, while prime numbers have only two factors, and composite numbers have more than two.
- In number systems, these numbers serve as digits. Binary uses 0 and 1 as common digits, while other systems use digits from 0 to 9. Understanding various types of numbers and their systems is essential in mathematics.
Classification of Numbers
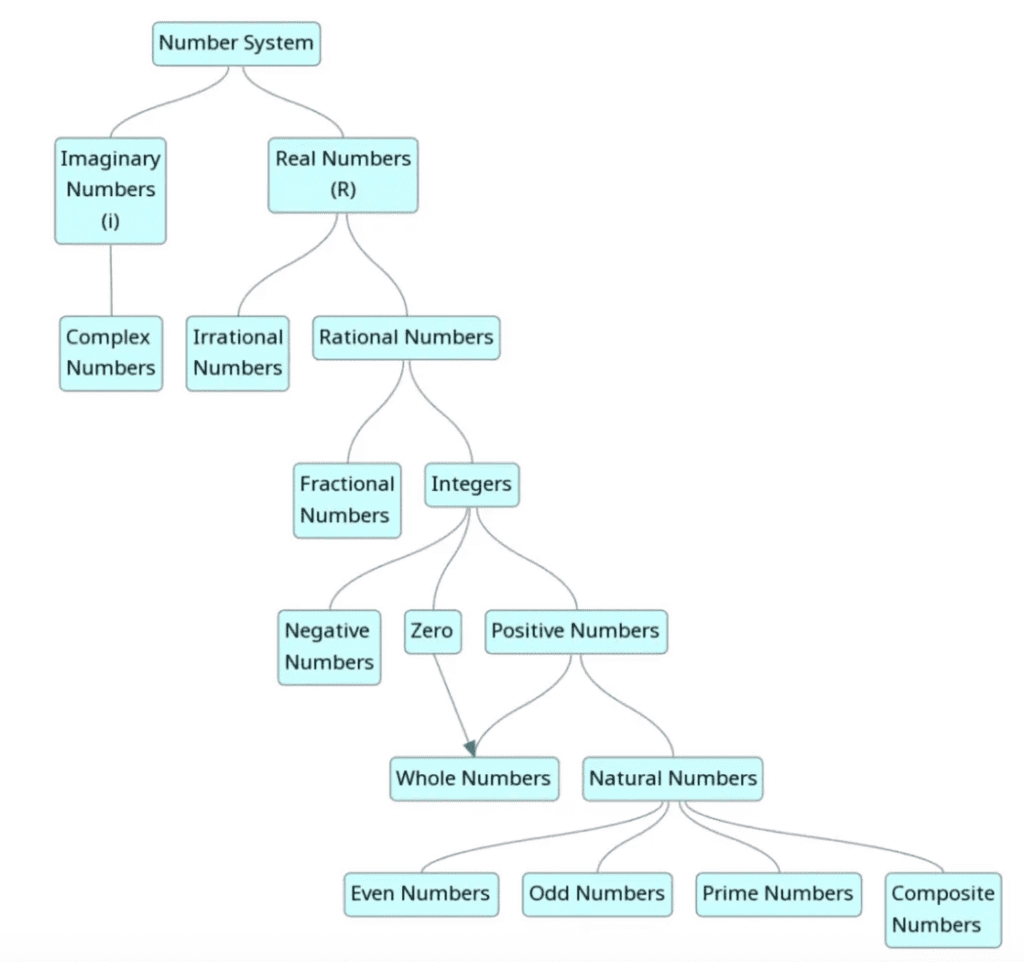
1. Real Numbers and Imaginary Numbers
Real numbers include the set of rational and irrational numbers.
- Rational numbers can be expressed as fractions, such as -3/4 or 5/2, while irrational numbers, like π (pi) or √2 (square root of 2), cannot be represented as fractions and have non-repeating, non-terminating decimal expansions.
- Real numbers can be positive or negative, whole or fractional, and they can be located on the number line.

- On the other hand, imaginary numbers involve the imaginary unit "i," where i² = -1. Complex numbers combine real and imaginary components, written in the form a + bi, where 'a' and 'b' are real numbers.
Examples of imaginary numbers include 2i, -3i, and (1 + 4i). The interplay between real and imaginary numbers forms the foundation for complex analysis in mathematics.
2. Rational and Irrational Numbers
Rational Numbers
A rational number is a type of real number, which is in the form of p/q where q is not equal to zero.
- Any fraction with non-zero denominator is a rational number.
- Some of the examples of rational numbers are 1/2, 1/5, 3/4, and so on.
Irrational Numbers
A number that cannot be expressed as the ratio of one over another is known as irrational numbers and it is represented by the symbol ”P”. Example: π (pi), √2
- All square and cube roots of natural numbers that are not perfect squares or perfect cubes are irrational.
- All operations like addition, subtraction, multiplication, and division that apply to rational numbers also apply to irrational numbers.
- When an expression includes both a rational and an irrational number, they must stay together throughout the solution. In other words, once an irrational number appears, it can only be eliminated if it is multiplied or divided by the same irrational number.
3. Integers (Z)
The set including all whole numbers and their negatives is called a set of integers. It is denoted by Z, and Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
They are further classified into Negative integers, Neutral integers and positive integers.
(a) Negative integers (Z-)
All integers lesser than Zero is called negative integers.
Z− = {- 1, - 2, - 3…- ∞ }
(b) Neutral integers (Z0)
Zero is the only integer that is neither negative nor positive and it is called a neutral integer.
(c) Positive integers (Z+)
All integers greater than zero are called positive integers.
Z+ = {1, 2, 3, …….., ∞ }.
4. Whole Numbers
The set of numbers that includes all natural numbers along with zero is called whole numbers.
Whole numbers are also known as non-negative integers.
5. Natural Numbers (N)
The numbers 1, 2, 3, 4, 5…are known as natural numbers. The set of natural numbers is denoted by N.
- All positive integers are natural numbers, and therefore, there are infinite natural numbers.
- Hence, N = {1, 2, 3, 4…}. The natural numbers are further divided as even, odd, prime etc.
- Whole Numbers (W): All natural numbers together with ‘0’ are collectively called whole numbers. The set of whole numbers is denoted by W, and W = {0, 1, 2, 3, ……}
6. Even and Odd Numbers
All numbers divisible by 2 are called even numbers.
Example: 2, 4, 6, 8, 10.…
Even numbers can be expressed in the form 2n, where n is an integer.
Thus 0, - 2, − 6, etc. are also even numbers.
All numbers not divisible by 2 are called odd numbers.
Odd numbers can be expressed in the form (2n + 1) where n is an integer.
Example:- 1, − 3, − 5…1, 3, 5, 7, 9…
7. Prime Numbers
A natural number that has no other factors besides itself and unity is a prime number.
Examples: 2, 3, 5, 7, 11, 13, 17, 19 …
On the contrary, a number which has more than two factors is called a composite number.
Important Observations About Prime Numbers
- A prime number greater than 3, when divided by 6 leaves either 1 or 5 as the remainder.
- Hence, a prime number can be expressed in the form of 6K ± 1 or 6K ± 5.
- But the converse of this observation is not true, that a number leaving a remainder of 1 or 5 when divided by 6 is not necessarily a prime number.
Example: 25, 35, etc.
Some Properties of Prime Numbers
- The lowest prime number is 2.
- Number 2 is also the only even prime number.
- The lowest odd prime number is 3.
- The remainder when a prime number p ≥ 5 is divided by 6 is 1 or 5.
- The remainder of the division of the square of a prime number p ≥ 5 divided by 24 is 1.
- For prime numbers, p > 3, p² - 1 is divisible by 24.
- The remainder of the division of the square of a prime number p ≥ 5 divided by 12 is 1.
- If a and b are any two odd prime numbers, then a2 - b2 as well as a2+b2 are composite numbers.
How to check whether a number is prime or not
To check whether a number N is prime, adopt the following process
- Take the Square root of the number.
- Round off the square root to the immediately higher integer. Call this number z.
- Check for divisibility of the number N by all prime numbers below z.
- If there is no prime number below the value of z that divides N then the number N will be prime.
- If a number has no prime factor equal to or less than its square root, then the number is a prime number.
To illustrate:
The value of √239 lies between 15 to 16. Hence, take the value of z as 16.
Prime numbers less than or equal to 16 are 2,3,5,7,11 and 13. 239 is not divisible by any of these. Hence, you can conclude 239 is a prime number.
Finding Prime Numbers: The Shortcut Method
- In most competitive exams, checking if a number is prime often focuses on 2-digit or 3-digit numbers between 100 and 200.
- There is no need to check divisibility by 5 since it's easy to identify; numbers divisible by 5 end in 0 or 5.
- Thus, there’s no risk of mistakenly identifying a number like 45 as prime.
- Therefore, when checking prime numbers below the square root of a number, 5 is excluded from testing.
- The same exclusion applies to all even numbers (except 2, which is a prime number).
Checking Whether a Number is Prime (For Numbers below 49)
- For numbers below 49, you only need to check if the number is divisible by 3. Since 47 isn't divisible by 3, it is a prime number.
- We are not checking for divisibility by 2, 5 or 7(the square of 7 is greater than 49).
Checking Whether a Number is Prime (For Numbers above 49 and below 121)
- This can be checked with testing divisibility by 3 and 7.
- However, if you remember that 77, 91, and 119 are not prime, you can identify prime numbers below 121 by only checking if they’re divisible by 3.
- This is because the odd numbers between 49 and 121 that are divisible by 7 are 63, 77, 91, 105, and 119. Among these, only 91 and 119 might mistakenly be seen as prime. But numbers like 77 and 105 are clearly not prime.
- So, for numbers between 49 and 121, just check if they’re divisible by 3. If they aren’t and they’re not 91 or 119, then they are prime numbers. For example, 61 is prime because it isn’t divisible by 3 and it’s neither 91 nor 119.
Checking Whether a Number is Prime (For Numbers above 121 and below 169)
- This can be checked with testing divisibility by 3, 7 and 11.
- However, if you remember that 133, 143, and 161 are not prime, you can identify prime numbers between 121 and 169 by only checking if they’re divisible by 3.
- Here’s why: The odd numbers between 121 and 169 that are divisible by 7 or 11 are 133, 143, 147, 161, and 165. Among these, 133, 143, and 161 might mistakenly be thought of as prime if you don’t check divisibility by 7 or 11. The number 147 will be shown as not prime when you check divisibility by 3, and you can easily tell 165 isn’t prime without further checking.
- So, for numbers between 121 and 169, you can find if a number is prime by just checking divisibility by 3.
- For example, 149 is prime because it’s not divisible by 3 and isn’t one of the numbers 133, 143, or 161.

Must Know
1 to 25 ⇒ 9 prime numbers
1 to 50 ⇒ 15 prime numbers
1 to 100 ⇒ 25 prime numbers
1 to 200 ⇒ 45 prime numbers
Example: If a, a + 2, a + 4 are consecutive prime numbers. Then how many solutions ‘a’ can have?
(a) One
(b) Two
(c) Three
(d) More than three
Correct Answer is Option (a)
- No even value of ‘a’ satisfies this. So ‘a’ should be odd.
- But out of three consecutive odd numbers, at least one number is a multiple of 3.
- So, the only possibility is a = 3 and the numbers are 3, 5, 7.
8. Composite Numbers
A composite number has other factors besides itself and unity.
- Every composite number n can be factored into its prime factors.
- This can be written as: n= p1m . p2n ... pks, where p1, p2 ... pk are prime factors and m, n ... k are natural numbers.
- For instance, 24 = 23 . 3, and 84 = 7 . 3 . 22
- This representation of a composite number is known as the standard form of a composite number.
Example: 8, 72, 39, etc.
- On the basis of the fact that a number with more than two factors is a composite, we have only 34 composites from 1 to 50 and 40 composites from 51 to 100.
Note: 1 is neither a prime number nor a composite number.
9. Perfect Numbers
A number is said to be a perfect number if the sum of all its factors excluding itself (but including 1) is equal to the number itself or the sum of all the possible factors of the number is equal to twice the number.
- If the factors of any perfect number other than 1 are written and the reciprocal of them are added together, then the result is always unity.
- Example: 6 is a perfect number because the factors of 6, i.e., 1, 2 and 3, add up to the number 6 itself.
Also,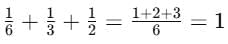 (Unity)
(Unity) - Other examples of perfect numbers are 28, 496, 8128, etc.
As of 2025, only 51 known perfect numbers (all even, none odd).
10. Fractions
A fraction denotes the part or parts of a unit.
Several types of fractions are:
- Common Fraction: Fractions whose denominator is not 10 or a multiple of it.
Example: 2/3, 17/18 - Decimal Fraction: Fractions whose denominator is 10 or a multiple of 10.
- Proper Fraction: In this the numerator < denominator.
Example: 2/10, 6/7, 8/9 etc. Hence its value < 1. - Improper Fraction: In these the numerator > denominator
Example: 10/2, 7/6, 8/7 etc. Hence its value > 1. - Mixed Fractions: When an improper fraction is written as a whole number and a proper fraction, it is called a mixed fraction.
Example: 7/3 can be written as 2 + 1/3 = 2(1/3)
11. Decimal Numbers
A decimal number is a number with a decimal point in it. For example, 1.5, 3.22, 829.234
- When we divide any number by another number, we either get a terminating decimal fraction or a non-terminating decimal fraction.
- Terminating decimal fractions are the numbers that have a fixed or a finite number of digits after the decimal point
- Non-terminating decimal fractions on the basis of the occurrence of digits after the decimal can be classified as follows:
1. Pure Recurring Decimals: A decimal in which all the figures after the decimal point repeat is called a pure recurring decimal.
Examples: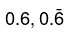 are examples of pure recurring decimals.
are examples of pure recurring decimals.
2. Mixed Recurring Decimals: A decimal in which some figures do not repeat and some of them are repeated is called a mixed recurring decimal.
Examples:
3. Non-Recurring Decimals: A decimal number in which the figure doesn’t repeat itself in any pattern is called a non-terminating non-recurring decimal and is termed as an irrational number.
Converting a recurring fraction into decimals:
All recurring decimals can be converted into fractions. Some of the common types can be 0.33…..,0.1232323…, 5.33…., 14.23636363…. etc.
(a) Pure Recurring to Fractions
Funda 1: If a number is of the form of 0. ababab……. then divide the repeating digits with as many 9’s as we have repeated digits.
Example: 0.363636...= 36/99 = 4/11
(b) Mixed Recurring to Fractions
Funda 2: If N = 0. abcbcbc…. Then N = abc - a/990
Repeated & non-Repeated digits - Non-Repeated digits/ As many 9's as repeated digits followed by as many zero as non-repeated digits
Example: 0.25757...= 257 - 2/990 = 255/990 = 17/66
Funda 3. If N = a. bcbc…. Then
Write N = a + 0. bcbc….Proceed as Funda 1
5.3636… = 5 + 0.3636… = 5 + 36/99 = 59/11
12. The Concept of the Number Line
A number line is a straight line that extends infinitely in both directions, with negative infinity on the left and positive infinity on the right.
 Number Line
Number Line
- The distance between any two points on the number line is obtained by subtracting the lower value from the higher value.
- Another way is to start from the smaller number and see how much you need to add to reach the larger number.
- For example: The distance between 7 and –4 is 7 – (–4) = 11.
Divisibility
- As the name suggests, divisibility tests or division rules in Maths help one to check whether a number is divisible by another number without the actual method of division.
- A number x is considered to be divisible by another number y if x can be divided by y without leaving any remainder.
- In general, when an integer 𝐼 is divided by a natural number 𝑁, there is a unique pair of numbers 𝑄 (the quotient) and 𝑅 (the remainder). This can be expressed as:
𝐼 = 𝑄𝑁 + 𝑅 - For any integer 𝐼 and any natural number 𝑁, there is a unique pair of numbers 𝑄 and 𝑅 such that 𝐼 =𝑄𝑁 + 𝑅, where 𝑄 is an integer, 𝑁 is a natural number (or zero), and 0 ≤ 𝑅 < 𝑁 (meaning the remainder must be a whole number less than 𝑁). If the remainder 𝑅 is zero, we say that 𝐼 is divisible by 𝑁.
Note: Even when we divide a negative number by a natural number N, the remainder remains non-negative.
For instance, when we divide –32 by 7, the remainder is actually +3, not –4, which might be surprising.
This is because the remainder is always non-negative.
So, when we divide –32 by 7, the quotient is –5 and the remainder is +3.
Theorems of Divisibility
 Theorems of Divisibility
Theorems of Divisibility
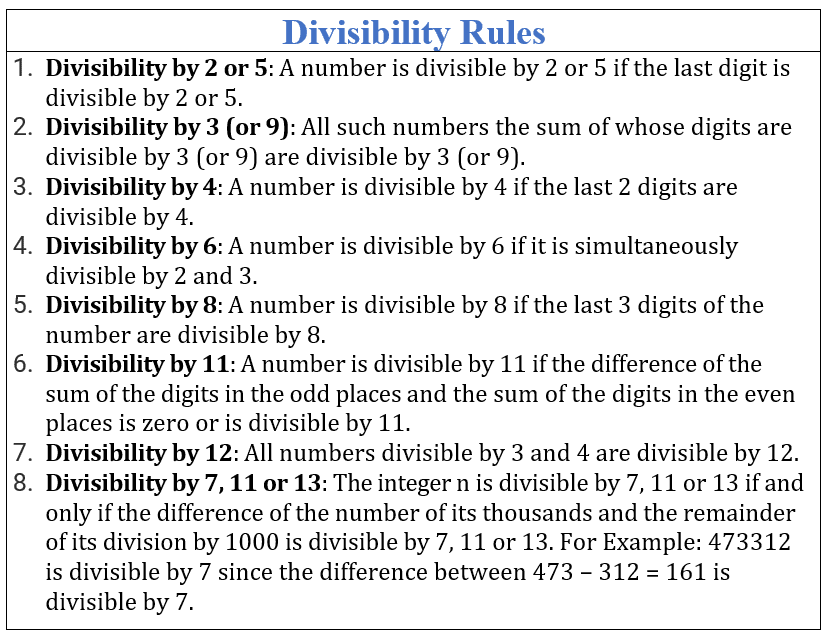
Divisibility Rules
1. Divisibility Rule of 1
- Every number is divisible by 1. The divisibility rule for 1 doesn’t have any conditions. Any number divided by 1 will give the number itself, irrespective of how large the number is.
- Example: 3 is divisible by 1, and 3000 is also divisible by 1 completely.
2. Divisibility Rule of 2
- If a number is even or a number whose last digit is an even number, i.e., 2,4,6,8, including 0, it is always completely divisible by 2.
- Example: 508 is an even number and is divisible by 2, but 509 is not. The procedure to check whether 508 is divisible by 2 or not is as follows:
⇒ Consider the number 508
⇒ Just take the last digit 8 and divide it by 2
⇒ If the last digit 8 is divisible by 2 then the number 508 is also divisible by 2.
3. Divisibility Rules for 3
- Divisibility rule for 3 states that a number is completely divisible by 3 if the sum of its digits is divisible by 3.
- Example: Consider a number, 308. To check whether 308 is divisible by 3 or not, take the sum of the digits (i.e. 3+0+8= 11).
Now check whether the sum is divisible by 3 or not.
If the sum is a multiple of 3, then the original number is also divisible by 3.
Here, since 11 is not divisible by 3, 308 is also not divisible by 3. - Similarly, 516 is divisible by 3 completely as the sum of its digits i.e. 5+1+6=12, is a multiple of 3.
4. Divisibility Rule of 4
- If the last two digits of a number are divisible by 4, then that number is a multiple of 4 and is completely divisible by 4.
- Example: Take the number 2308. Consider the last two digits i.e. 08.
- As 08 is divisible by 4, the original number 2308 is also divisible by 4.
5. Divisibility Rule of 5
- Numbers, which last with digits, 0 or 5 are always divisible by 5.
- Example: 10, 10000, 10000005, 595, 396524850, etc.
6. Divisibility Rule of 6
- Numbers which are divisible by both 2 and 3 are divisible by 6. That is, if the last digit of the given number is even and the sum of its digits is a multiple of 3, then the given number is also a multiple of 6.
- Example: 630, the number is divisible by 2 as the last digit is 0.
The sum of digits is 6+3+0 = 9, which is also divisible by 3.
Hence, 630 is divisible by 6.
7. Divisibility Rules for 7
The rule for divisibility by 7 is a bit complicated which can be understood by the steps given below:
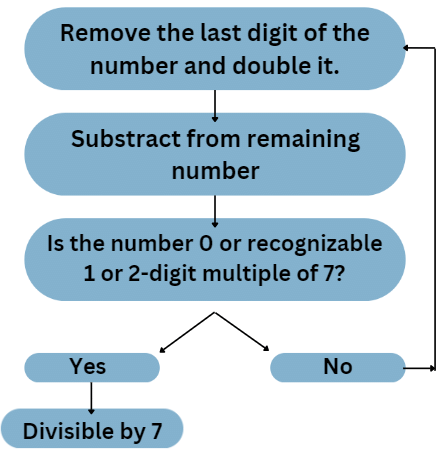
Example:Is 1073 divisible by 7?
- From the rule stated remove 3 from the number and double it, which becomes 6.
- Remaining number becomes 107, so 107-6 = 101.
- Repeating the process one more time, we have 1 x 2 = 2.
- Remaining number 10 – 2 = 8.
- As 8 is not divisible by 7, hence the number 1073 is not divisible by 7.
8. Divisibility Rule of 8
- If the last three digits of a number are divisible by 8, then the number is completely divisible by 8.
- Example: Take number 24344.
Consider the last three digits i.e. 344.
As 344 is divisible by 8, the original number 24344 is also divisible by 8.
9. Divisibility Rule of 9
- The rule for divisibility by 9 is similar to divisibility rule for 3. That is, if the sum of digits of the number is divisible by 9, then the number itself is divisible by 9.
- Example: Consider 78532, as the sum of its digits (7+8+5+3+2) is 25, which is not divisible by 9,
hence 78532 is not divisible by 9.
10. Divisibility Rule of 10
- Divisibility rule for 10 states that any number whose last digit is 0, is divisible by 10.
- Example: 10, 20, 30, 1000, 5000, 60000, etc.
11. Divisibility Rules for 11
If the difference of the sum of the alternative digits of a number is divisible by 11, then that number is divisible by 11 completely.
In order to check whether a number like 2143 is divisible by 11, below is the following procedure:
- Group the alternative digits i.e. digits which are in odd places together and digits in even places together. Here 24 and 13 are two groups.
- Take the sum of the digits of each group i.e. 2+4=6 and 1+3= 4
- Now find the difference of the sums; 6-4=2
- If the difference is divisible by 11, then the original number is also divisible by 11. Here 2 is the difference which is not divisible by 11.
- Therefore, 2143 is not divisible by 11.
12. Divisibility Rule of 12
- If the number is divisible by both 3 and 4, then the number is divisible by 12 exactly.
- Example:5864
⇒ Sum of the digits = 5 + 8 + 6 + 4 = 23 (not a multiple of 3)
⇒ Last two digits = 64 (divisible by 4)
⇒ The given number 5864 is divisible by 4 but not by 3; hence, it is not divisible by 12.
13. Divisibility Rules for 13
- For any given number, to check if it is divisible by 13, we have to add four times of the last digit of the number to the remaining number and repeat the process until you get a two-digit number.
- Now check if that two-digit number is divisible by 13 or not. If it is divisible, then the given number is divisible by 13.
- Example: 2795 ⇒ 279 + (5 x 4)
⇒ 279 + (20) ⇒ 299 ⇒ 29 + (9 x 4) = 29 + 36 = 65
Number 65 is divisible by 13, 13 x 5 = 65.
Common Pitfalls:
For 3 or 9, ensure the sum of digits is checked, not the product.
For 7, follow the exact steps to avoid miscalculation.
Practice Questions:
Easy: Is 342 divisible by 3? (Answer: Yes, 3+4+2=9)
Medium: Is 1073 divisible by 7? (Answer: No, as shown in the original example)
Hard: How many numbers from 1 to 100 are divisible by both 3 and 4? (Answer: 8, using LCM=12)
Mnemonic: “Even 2, Sum 3, Last-two 4, Zero-five 5” for quick recall of rules for 2, 3, 4, 5.
Properties of Number
- Every number has the same unit’s digit at its fifth power as it has at its first power. Thus, the standard method that can be followed is to divide the power by 4, find the remaining power and check the unit’s digit in that number. This shortcut can be applied because you will always get the same unit’s digit as otherwise.
- For calculating the number of zeroes at the end of the factorial of a number, you should divide the number by 5, the quotient obtained is again divided by 5 and so on till the last quotient obtained is smaller than 5. The sum of all the quotients is the number of 5s, which then becomes the number of zeroes in the given number.
- The digital root of a number is the sum of the digits, over and over again, till it becomes a single-digit number. For example, the digital root of 87984 will be 8 + 7 + 9 + 8 + 4 ⇒ 36 = 3 + 6 ⇒ 9.
- When the concept of Euler theorem is used and the dividend and divisor happen to be co-prime, the remainder questions become very easy.
- The product of 3 consecutive natural numbers is divisible by 6.
For example, let n, n+1 and n+2 be three consecutive natural numbers and P (n) be their product.
Then, P(n)=n(n+1)(n+2)
We have,
P(1)=1×2×3=6, which is divisible by 3 and 6.
P(2)=2×3×4=24, which is divisible by 3, 8 and 6.
P(3)=3×4×5=60, which is divisible by 3 and 6.
P(4)=4×5×6=120, which is divisible by 3, 8 and 6.
Hence, P(n) is divisible by 3 and 6 for all n∈ N. - The product of 3 consecutive natural numbers, the first of which is an even number, is divisible by 24.
- The sum of a two-digit number and a number formed by reversing its digits is divisible by 11.
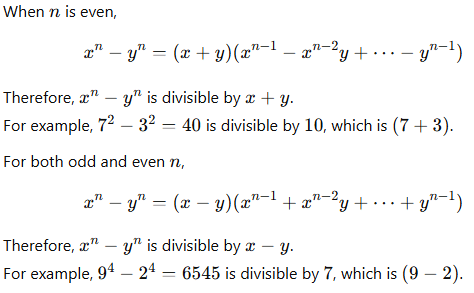
Absolute Value of a Number
- The modulus of a number is the absolute value of the number or we can say the distance of the number from the origin. The absolute value of a number is defined as:
|a| = a, if a ≥ 0
= - a, if a ≤ 0
|a| is read as MODULUS of a - Example: |79| = 79 &
| - 45| = - (- 45) = 45
Also, | x - 3 | = x - 3, if x ≥ 3
= 3 - x, if x < 3.
Solved Examples
Example 1. N = (18n2 + 9n + 8)/n; where N belongs to an integer. How many integral solutions of N are possible?
The given expression can be broken as: 18n2/n + 9n/n + 8/n. This gives us: 18n + 9 + 8/n.
- Now we can see that whatever the value of ‘n’, 18n + 9 will always give an integral value. Therefore, it now depends upon 8/n the only ⇒ n can have any integral value, which is a factor of 8.
- The integers, which will satisfy this condition are ±1, ±2, ±8, ±4. Thus, in total, n can take 8 values.
Example 2. N = 960. Find the total number of factors of N.
- The number of divisors of a composite number: If D is a composite number in form D = ap × bq × cr, where a, b, c are primes, then the no. of divisors of D, represented by n is given by n = (p+1)(q+1)(r +1).
- Following the same, after dividing 960 into prime factors: 26 × 31 × 51, we can calculate the total number of factors as (6+1). (1+1).(1+1) = 28.
Example 3. Find the unit digit of the following expression: (123)34 × (876)456 × (45)86.
- Whenever an even unit digit Number is present and a Number with 5 at the unit digit are present, they will always give a 0 at the unit digit, no matter if any other number is present or not.
Example 4. What will be the number of zeroes at the end of the product of the first 100 natural numbers?
Example 5. Which letter should replace the $ in the number 2347$98, so that it becomes a multiple of 9?
- As you know that if the sum of all the digits is divisible by 9, then the number is divisible by 9.
- Now sum of the given digits is 2 + 3 + 4 + 7 + 9 + 8 = 33 + $. Now think the next multiple of 9 after 33 i.e. 36. This means you add 3 in this. The value of $ is 3.
Example 6. In a party, there are 20 people present. If each of them shakes hands with all the other persons, in total, how many handshakes will take place?
- Out of 20 persons, the first person will shake hand with 19 persons.
- The second person will shake hand with 18 persons (because he has already shaken hand with first person).
- The third person will shake hand with 17 persons and so on.
- The second last person shakes hand with only one person.
- And last will shake hand with none (because he has already shaken hand with all persons).
- In order to find the total number of handshakes, you have to add all the natural numbers from 1 to 19, i.e. ∑ 19. ∑19 = 19 x 20/2 = 190 handshakes.
Example 7. What is the remainder when 2354789341 is divided by 11?
- Odd place digit sum (O) = 1 + 3 + 8 + 4 + 3 = 19.
- Even place digits sum (E) = 4 + 9 + 7 + 5 + 2 = 27.
- Difference (D) = 19 - 27 = - 8
- Remainder = 11 - 8 = 3.
Tip: When any number with even number of digits is added to its reverse, the sum is always divisible by 11. e.g. 2341 + 1432 = 3773, which is divisible by 11.
⇒ Any number written 6 times consecutively will be divisible by 7 and 13.
Example 8. If 567P55Q is divisible by 88; Find the value of P + Q.
(a) 11
(b) 12
(c) 5
(d) 6
(e) 10
Correct Answer is Option (e)
- The number is divisible by 8 means; the number formed by the last 3 digits should be divisible by 8, which are 55 Q. Only Q = 2 satisfies this.
- From the divisibility rule of 11, (2 + 5 + 7 + 5) - (5 + P + 6) is divisible by 11. So 8-P is divisible by 11.
- If P= 8, then only it is possible. So P = 8 and Q = 2.
- So, P + Q = 10.
Example 9. If the first 100 natural numbers are written side by side to form a big number and it is divided by 8. What will be the remainder?
(a) 1
(b) 2
(c) 4
(d) 7
(e) Cannot be determined
Correct Answer is Option (c)
- The number is 1234…..9899100.
- According to the divisibility rule of 8, we will check only the last 3 digits.
- If 100 is divided by 8, the remainder is 4.
Example 10. What will be the remainder when 4444……..44 times is divided by 7?
(a) 1
(b) 2
(c) 5
(d) 6
(e) 0
Correct Answer is Option (b)
- If 4 is divided by 7, the remainder is 4.
- If 44 is divided by 7, the remainder is 2.
- If 444 is divided by 7, the remainder is 3.
- By checking like this, we come to know that 444444 is exactly divisible by 7.
- So if we take six 4’s, it is exactly divisible by 7.
- Similarly, twelve 4’s is also exactly divisible by 7 and 42 4’s will be exactly divisible by 7. So out of 44 digits, the remaining two 4s give a remainder of 2.
Co-Prime or Relatively Prime Numbers
Two or more numbers that share no common factor are called co-prime or relatively prime. In other words, their greatest common factor is 1.
If two numbers m and n are relatively prime, and a natural number x is divisible by both m and n individually, then x is also divisible by mn.
Key Concept 1: Recognising two numbers as co-prime is important when they appear in the denominators of fractions.
- This concept is best explained with an example:
Consider M/8 + N/9, where M isn't divisible by 8 and N isn't divisible by 9. These numbers are co-prime, meaning they have no common factors other than 1. When two numbers are co-prime, the result is a decimal fraction, rather than an integer. This is because 8 and 9 are co-prime, and the decimal results from dividing by co-prime numbers don’t match each other. - This concept is highly significant when solving problems, especially when dealing with linear equations in word problems.
Example: Find all four-digit numbers of the form 25x7y that are divisible by 36.
Sol:Since 36 is the product of two co-prime numbers, 4 and 9, the number 25x7y must be divisible by both 4 and 9 for it to be divisible by 36.
Divisibility by 4: For divisibility by 4, the last two digits of the number (7y) must be divisible by 4. The possible values for y that make 7y divisible by 4 are 2 and 6. So, y can be 2 or 6.
Divisibility by 9: For divisibility by 9, the sum of the digits of the number must be divisible by 9. The sum of the digits is
If y=2, the sum is 2+5+x+7+2=16 + x.
For this to be divisible by 9, 16 + x must be a multiple of 9. The possible value of x is 2 (since 16 + 2 = 18, which is divisible by 9).
If y=6, the sum is 2+5+x+7+6=20 + x.
For this to be divisible by 9, 20 + x must be a multiple of 9. The possible value for x is 7 (since 27 is divisible by 9).Thus, the numbers 25272 and 25776 are divisible by 36.
Key Concept 2: Another way to determine if two numbers are co-prime is by examining their prime factors. For two or more numbers to be co-prime, their prime factors must not have any common elements.
For example, if A and B are co-prime, and A = 2nx 3m, then the prime factors of B must not include 2 or 3. Instead, would be made up of other prime numbers like 5, 7, 11, etc., but it cannot have 2 or 3 as factors.
Always Keep in Mind
- The number 1 is neither prime nor composite.
- 2 is the only even number that is prime.
- (xn + yn) is divisible by (x + y), when n is an odd number.
- (xn - yn) is divisible by (x + y), when n is an even number.
- (xn - yn) is divisible by (x - y), when n is an odd or an even number.
- A sum of 5 consecutive whole numbers will always be divisible by 5.
- The difference between 2 numbers (xy) - (yx) will always be divisible by 9.
- The square of an odd number when divided by 8 will always give 1 as a remainder.
- Every square number is a multiple of 3 or exceeds a multiple of 3 by unity.
- Every square number is a multiple of 4 or exceeds a multiple of 4 by unity.
- If a square number ends in 9, the preceding digit is even.
- If m and n are two integers, then (m + n)! is divisible by m! n!
- (a)n / (a + 1) leaves a remainder of
- The product of n consecutive numbers is always divisible by n!.
Example 1. If ‘X’ is an even number; Y is an odd number, then which of the following is even?
(a) X2 + Y
(b) X + Y2
(c) X2 + Y2
(d) X2Y2
(e) None of these
Correct Answer is Option (d)
- Since X is even, X2 is even.
- Y is odd, Y2 is odd.
- So options (1), (2), (3) are even + odd = odd.
- Option (4) is (even) (odd) = Even.
Example 2. What is the difference between 0.343434....…and 0.2343434…… in fraction form?
(a) 6/55
(b) 6/11
(c) 9/55
(d) 9/13
(e) 5/11
Correct Answer is Option (a)
0.343434.....= 34/99 and 0.23434.... = 234 - 2/990 = 232/990
∴ Difference = 34/99 - 232/990 = 108/990 = 6/55
Example 3. How many of the following numbers are divisible by at least 3 distinct prime numbers 231, 750, 288 and 1372?
(a) 0
(b) 1
(c) 2
(d) 3
(e) 4
Correct Answer is Option (c)
- 231 = 3 × 7 × 11 (3 prime factors)
- 750 = 2 × 3 × 53 (3 prime factors)
- 288 = 25 × 32 (only 2 prime factors)
- 1372 = 22 × 73 (only 2 prime factors)
So, only 231 & 750 has 3 prime factors
Example 4. n3 + 6n2 + 11n + 6 (where n is a whole no) is always divisible by
(a) 4
(b) 5
(c) 6
(d) 8
(e) 12
Correct Answer is Option (c)
- n3 + 6n2 + 11n + 6 = (n + 1) (n + 2) (n + 3).
- Product of 3 consecutive numbers is always divisible by 3! = 6. (or)Take n = 0, 1, 2, 3 and check it is always divisible by 6.
Example 5. What is the remainder, if 351 × 352 × 353 × - - - - - - - × 356 is divided by 360?
(a) 0
(b) 1
(c) 2
(d) 3
(e) 359
Correct Answer is Option (a)
- Since the given is the product of 6 consecutive numbers, it is always divisible by 6! = 720.
- It is divisible by 360 also. So, the remainder will be 0.
The Concepts of HCF & LCM
Highest Common Factor (HCF)
- Common factor: If two numbers A and B are exactly divisible by a number X, then X is a common divisor or factor of A and B.
- Highest Common Factor: It is the highest factor common to two or more numbers under consideration. It Is also called GCF or GCD (Greatest Common Factor or Greatest Common Divisor). e.g. HCF of 4 and 8 = 4, HCF of 125 and 200 = 25.
- To find the HCF of given numbers:
1. Break the given numbers into their prime factors.
2. The HCF will be the product of all the prime factors common to all the numbers.
Let us learn the process of finding HCF with the help of some solved examples.
Q1:Find the HCF of 96, 36 and 18.
Sol:First break each number into their prime factors.
96 =2 x 3 x 2 x 2 x 2 × 2
36 = 2 x 3 x 2 x 3
18 = 2 x 3 x 3
Take all the common factors of these numbers and multiply them.
Therefore, the HCF of 96, 36 and 18 is the product of the highest number of common factors in the given numbers i.e., 2 x 3 = 6. In other words, 6 is the largest possible integer, which can divide 96, 36 and 18 without leaving any remainder.
Q2: Find the HCF of 42 and 70.
Sol:
42 = 3 x 2 x 7
70 = 5 x 2 x 7
Hence, HCF is x 7 = 14.
Q3: Find the HCF of numbers 144, 630 and 756
Sol:
144 = 24 x 32
630 =2×32x 5 x7
756 = 22 x 33 x7
Hence, HCF of 144, 630, 756 = 2 x 32 = 18.
Important:
- HCF of two prime numbers is always 1
- HCF of co-prime numbers is always 1
Shortcut Method for Finding the HCF
Let's learn a faster way to find the HCF (Highest Common Factor) of a set of numbers using examples.
Example 1: Find the HCF of 39, 78, and 195.
Sol:Look at the step-by-step method:
Look at the differences between the numbers.
- Take the difference between any two numbers. The HCF must be a factor of these differences.
- The differences are:
- 78−39=39
- 195−39=156
- 195−78=117
- So, the HCF must divide 39, 156, and 117.
Start with the smallest difference (39).
- The HCF must be a factor of 39. The factors of 39 are:
- 1, 3, 13, and 39.
Check if the largest factor (39) divides all the numbers.
- Does 39 divide 78? Yes.
- Does 39 divide 195? Yes.
- So, the HCF of 39, 78, and 195 is 39.
Example 2: Find the HCF of 39, 78, and 182.
Sol:
- Find the differences between the numbers.
- 78−39=39
- 182−39=143
- 182−78=104
- Check the factors of 39 (1, 3, 13, 39).
- Does 39 divide 182? No.
- Try the next largest factor, 13.
So, the HCF of 39, 78, and 182 is 13.
- Does 13 divide 39? Yes.
- Does 13 divide 182? Yes.
LCM
The Least Common Multiple of two or more numbers is the smallest number which is exactly divisible by all of them. In other words, it is the product of the highest powers of all the prime factors of the given numbers.
To find the LCM of given numbers:
- Break the given numbers into their prime factors.
- The LCM will be the product of the highest power of all the factors that occur in the given numbers.
Let us take some solved examples.
Question: Find the LCM of 96, 36 and 18.
Solution:
First, Break each number into their prime factors
96 = 2 x 2 x 2 x 2 x 2 x 3 =25x 31
36 = 2 x 2 x 3 x 3 = 22 x 32
18 = 2x 3 x 3= 21 x 32
Therefore, LCM of 96, 36 and 18 is the product of the highest powers of all the prime factors, i.e. 25 x 32= 32 x 9 = 288.
That is, 288 is the smallest integer, which is divisible by 96, 36 and 18 without leaving any remainder.
Question:Find the LCM of 42 and 70
Solution:
42 = 3 x 2 x 7
70 = 5 x 2 x 7
Hence, LCM is 2 x 3 x 5 x 7 = 210.
Apart from the method ofprime factorization, there is another method of finding the LCM of given numbers and the method is known as the long division method. This method is quite helpful in getting LCM quickly if there are three or more than three numbers.
LCM by Division Method
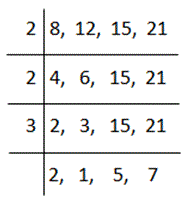
Write the numbers, separated by commas. Then divide them by prime factors in ascending order (e.g., 2, 3, 5, 7, etc.) one at a time. Then, after each division, write ‘ the quotient of each number that gets completely divided by the divisor (the prime number) below it. Leave the undivided numbers as they are. Continue doing this till you get prime factors as quotients in each column, The product of all the prime factors (divisors and quotients) will be the LCM.
Question: Find the LCM of 8, 12, 15 and 21
Solution:
Hence, LCM is 2x 2x 2x3x 5x 7= 840.
Important:
1. HCF of A, B and C is the highest divisor which can exactly divide A, B, and C.
2. LCM of A, B and C is the lowest dividend which is exactly divisible by A, B, and C.
There is one very important relationship, given below, between two numbers and their HCF and LCM. Many problems have appeared in
various competitive exams based on this relationship.
Example: LCM and HCF of two numbers are 2079 and 27 respectively. If one of the numbers is 189, find the other number.
Sol: The other number will be=
Hence, the required number =
Example:Two numbers are in the ratio 3: 5 and their LCM is 1500. Find the HCF of the numbers.
Sol:
Let the two number be 3X and 5X.
Hence their HCF = X using the formula given above, we get LCM = 3×5×X=15X
Or, 15X=1500 => X=100.
Therefore, the HCF of the numbers is 100
HCF and LCM of Fractions
We can use the following direct formula.
HCF of fractions= 
Similarly, LCM of fractions =
Example:Find the HCF and LCM of the two fractions 6/9, 12/15.
Sol:
The numerators are 6 and 12, their HCF = 6 and LCM =12
The denominators are 9 and 15, their LCM = 45 and HCF=3
Hence, the required HCF =and the LCM = 12/3=4.
Example: What is the greatest possible rate at which a man can walk 51 km and 85 km in an exact number of minutes?
Sol: To find the greatest possible rate at which the man can walk 51 km and 85 km in an exact number of minutes, we need to determine the largest common factor of 51 and 85 in terms of kilometers per minute. This problem is asking for the HCF (Highest Common Factor) of the distances 51 km and 85 km.
Step-by-Step Process:
1. Find the HCF of 51 and 85:
- The prime factors of 51 are: 51=3× 17
- The prime factors of 85 are: 85=5×17
The common factor between 51 and 85 is 17.
2. Result: The greatest possible rate at which the man can walk in an exact number of minutes is 17 km per minute, since 17 is the largest number that divides both 51 and 85 exactly.
Thus, the greatest possible rate is 17 kilometers per minute.
Remainders
- We know that when a number M is divided by another number N, and if M > N, then the remainder is calculated by subtracting the maximum possible multiple of N from M.
- In the process, the excess portion remaining after subtraction is calledthe remainder, the maximum multiple of N is called quotient, and M and N are called the dividend and divisor, respectively.
- We have the following relation among them:
Dividend = Quotient x Divisor + Remainder
Important points on the remainder
- The remainder is always less than the divisor.
- If the remainder is 0, then the divisor is called a factor of the dividend
- If the dividend is less than the divisor, then the remainder is the dividend itself.
E.g., 5 divided by 6, the remainder is 5 only.
- The remainder should always be calculated in its actual form. i.e. it should not be reduced into the simplest form.
E.g., Remainder of when 4 is divided by 6 is 4 and NOT 2.
The Remainder Theorem
The Remainder Theorem helps us find the remainder when a product is divided by a number without having to calculate the whole product. Let's break it down with the example of 17 x 23 divided by 12.
Step-by-Step Explanation:
Rewrite the numbers:We can express the numbers 17 and 23 in a way that includes 12:
17 = 12 + 5
23 = 12 + 11
So, we can rewrite the expression:
17 x 23 = (12+5) x (12+11)Expand the expression: Using the distributive property, expand the expression
(12+5)(12+11) = 12 x 12 + 12 x 11 + 5 x 12 + 5 x 11Identify the terms:
12 x 12 (is divisible by 12, so it leaves a remainder of 0)
12 x 11 (divisible by 12)
5 x 12 (divisible by 12)
Last term: 5 x 11Focus on the last term: The only term that affects the remainder when divided by 12 is 5 x 11
5 x 11 = 55Find the Remainder:Now, we need to find the remainder when 55 is divided by 12:
55 / 12 = 4 with a remainder of 7Thus, the remainder when 17 x 23 is divided by 12 is 7.
The Remainder Theorem simplifies the process of finding remainders by focusing only on the relevant terms after rewriting the numbers in relation to the divisor. In our example, we only needed to consider the last term
The Concept of the Negative Remainder
In mathematics, the remainder is always a non-negative integer. However, we can use the concept of negative integers to solve many questions easily and with less calculation.Let us take an example to understand it:
We know that remainder obtained when 15 is divided by 4 is 3 as 15 is 3 more than the nearest multiple of 4 i.e. 12.
Here we are comparing 15 with 12 (the largest multiple of 4 less than equal to 15 ) and found that 15 is 3 more than 12 and hence the excess portion is 3 which is the remainder.
Instead of comparing with 12, if we compare 15 with 16 (another multiple of 4 close to 15) we can say that 15 is 1 LESS than 16. Or there is a deficiency of 1 in 15 to make it divisible by 4. This deficient number is called a negative remainder. i.e. we can say that the remainder when 15 is divided by 4 is -1.
Conversion from negative remainder to the corresponding positive remainder and vice versa
- Remainder obtained when N is divided by 5 is -2, then the positive remainder is given by 5-2 = 3. Similarly, if 4 is the positive remainder obtained when some number is divided by 7, then the negative remainder is given by 4-7 = -3.
- We will be using this concept in solving few examples to understand the application of negative remainders.
Note:Product, addition and subtraction of any two or more numbers has the same remainder when divided by any natural number, as the corresponding product, addition and subtraction of their remainders.
Let us understand this with an example:
Take a number N =. Now let us find the remainder when N is divided by 5.
One approach is that we first calculate the value of N =i.e. which is equal to 197. And then dividing this number by 5 to get the remainder = 2.
The other approachis that we calculate the remainders of each number given in N by dividing it by 5 and then use the corresponding mathematical operators with these remainders.
Remainder obtained when 24 is divided by 5 = 4
Remainder obtained when 8 is divided by 5 = 3
Remainder obtained when 12 is divided by 5 = 2
Remainder obtained when 7 is divided by 5 = 2
Replacing numbers with their corresponding remainders we get,Since 12 is greater than 5, we divided 12 by 5 again to get the final remainder = 2.
Note: The second approach might sound difficult or redundant for the given example. But the detailed explanations are given for understanding purposes, we will see how applying this second approach we can solve advanced problems.
Applying both positive remainder and the concept of negative remainder simultaneously in the above problem with the second approach:
Remainder obtained when 24 is divided by 5 = -1
Remainder obtained when 8 is divided by 5 = -2
Remainder obtained when 12 is divided by 5 = 2
Remainder obtained when 7 is divided by 5 = 2
Replacing numbers with their corresponding remainders we get,Hence the final remainder = 2.
Solved Examples
Question: What is the remainder when 123 × 124 × 125 is divided by 9?
Solution:
Remainder obtained when 123 is divided by 9 = -3
Remainder obtained when 124 is divided by 9 = -2
Remainder obtained when 123 is divided by 9 = -1
Final remainder = (-3)(-2)(-1) = -6. The required positive remainder = 9-6 = 3.
Question: What is the remainder when 1! + 2! + 3! + …. + 100! Is divided by 5.
Solution:
Observe that in the series 5! onwards every number is divisible by 5 i.e. the remainder in each case is 0.
So the required remainder is obtained by dividing only the first 4 numbers i.e.
Cyclicity
1. Digits 0, 1, 5 & 6:
When we observe the behaviour of these digits, they all have the same unit's digit as the number itself when raised to any power, i.e. 0n = 0, 1n =1, 5n = 5, 6n = 6.
5 2 = 25: Unit digit is 5, the number itself.
16 = 1: Unit digit is 1, the number itself.
04 = 0: Unit digit is 0, the number itself.
63 = 216: Unit digit is 6, the number itself.
Let's apply this concept to the following example.
Example: Find the unit digit of the following numbers:
2. Digits 4 & 9:
Both these numbers have a cyclicity of only two different digits as their unit's digit.
42 = 16: Unit digit is 6.
43 = 64: Unit digit is 4.
44 = 256: Unit digit is 6.
45 = 1024: Unit digit is 4.
92 = 81: Unit digit is 1.
93 = 729: Unit digit is 9.
It can be observed that the unit digits 6 and 4 are repeating in an odd-even order. So, 4 has a cyclicity of 2. Similar is the case with 9.
It can be generalised as follows:
 Example: Find the unit digit of the following numbers:
Example: Find the unit digit of the following numbers:

3. Digits 2, 3, 7 & 8:
These numbers have apower cycle of 4 different numbers.
21 = 2, 22 = 4, 23 = 8 & 24 = 16 and after that it starts repeating.
So, the cyclicity of 2 has 4 different numbers 2, 4, 8, 6.
31 = 3, 32 =9, 33 = 27 & 34 = 81 and after that it starts repeating.
So, the cyclicity of 3 has 4 different numbers 3, 9, 7, 1.
7 and 8 follow similar logic.
So these four digits, i.e., 2, 3, 7 and 8 have a unit digit cyclicity of four steps.
Cyclicity Table
The concepts discussed above are summarised in the given table.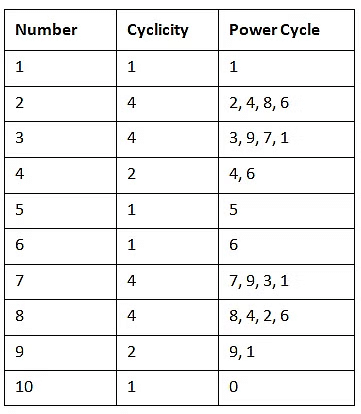
The power concept or cyclicity of a number helps us figure out the last digit of a number raised to a large power without actually calculating the whole thing. It's based on a repeating pattern that depends on the last digit of the number. A table helps us predict this last digit. Also, digits that appear once or twice are repeated every four times. So, each digit repeats every four times.
Number of Zeroes
1. Number Of Zeros in An Expression
Step 1
- Suppose you have to find the number of zeroes in a product: 24 × 32 × 17 × 23 × 19.
- We first get the series in terms of its prime factors i.e. 23∗31∗25∗171∗19∗23.
- As you can notice, this product will have no zeroes because it has no 5 in it.
- However, if you have an expression like 8 × 15 × 23 × 17 × 25 × 22
- The above expression can be rewritten in the standard form as: 23∗31∗51∗23∗17∗52∗21∗111
Step 2
- Zeroes are formed by a combination of 2 × 5.
- Hence, the number of zeroes will depend on the number of pairs of 2’s and 5’s that can be formed.
- In the above product, there are four twos and three fives. Hence, we shall be able to form only three pairs of (2 × 5).
- Hence, there will be 3 zeroes in the product.
2. Finding the Number of Zeros in a Factorial Value
- Method 1: Suppose you had to find the number of zeroes in 6!. 6! = 6 × 5 × 4 × 3 × 2 × 1 = (3 × 2) × (5) × (2 × 2) × (3) × (2) × (1).
Counting the number of 5 will give the answer. - Method 2: For finding the zeroes in 6! we use
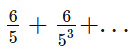 So we get 1 as the answer as all divisions after the first term in the series are in decimals, which we ignore.
So we get 1 as the answer as all divisions after the first term in the series are in decimals, which we ignore.
Q. 12 × 15 × 5 × 24 × 13 × 17
(a) 0
(b) 1
(c) 2
(d) 3
Ans: (c)
Sol: 22∗3∗3∗5∗5∗23∗3∗13∗17 = so pairs of (5*2) are 2, so we have 2 zeroes.
3. A Special Implication
- While solving 45!, 46!, 47!, 48!, 49!. Notice that the number of zeroes in each of the cases will be equal to 10.
- It is not difficult to understand that the number of fives in any of these factorials is equal to 10. The number of zeroes will only change at 50! (It will become 12).
- In fact, this will be true for all factorial values between two consecutive products of 5.
- Thus, 50!, 51!, 52!, 53! And 54! will have 12 zeroes (since they all have 12 fives). Similarly, 55!, 56!, 57!, 58! And 59! will each have 13 zeroes.
- While there are 10 zeroes in 49! There are 12 zeroes directly in 50!. This means that there is no value of a factorial which will give 11 zeroes. This occurs because to get 50! We multiply the value of 49! by 50. When you do so, the result is that we introduce two 5’s in the product. Hence, the number of zeroes jumps by two.
- Note: at 124! you will get 24 + 4 = 28 zeroes. At 125! you will get 25 + 5 + 1 = 31 zeroes. (A jump of 3 zeroes.)
Example: n! has 13 zeroes. The highest and lowest values of n?
(a) 57 and 58
(b) 59 and 55
(c) 59 and 6
(d) 79 and 55
Ans: (b)
Sol: At 55 we get 13 zeroes, since we know that 50! is 12 zeroes so till 54! we will have 12 zeroes. So 55 to 59! will have 13 zeroes.
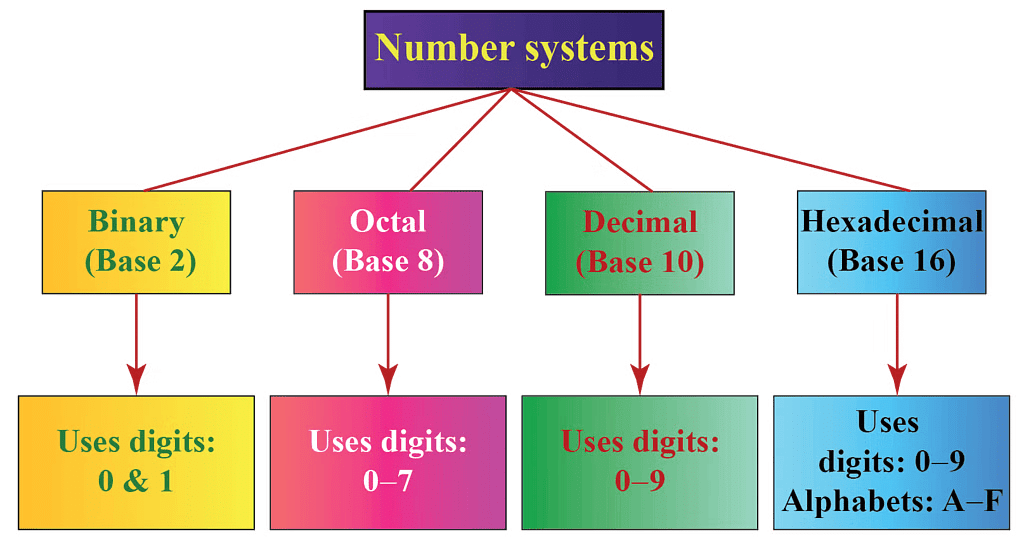
Base Systems
1. Decimal number system (Base-10)
2. Binary number system (Base-2)
3. Octal number system (Base-8)
4. Hexadecimal number system (Base-16)
1. Decimal number system (Base-10)
The decimal number system, with a base of 10, employs digits 0 to 9. Positions to the left of the decimal point represent powers of 10, indicating units, tens, hundreds, etc.
Example: 3567.89
In this example, the digit 3 is in the thousands place (103), the digit 5 is in the hundreds place (102), the digit 6 is in the tens place (101), the digit 7 is in the units place (100 or 1), the digit 8 is in the tenths place and the digit 9 is in the hundredths place.
2. Binary number system (Base-2)
Binary, or base-2, has only two digits, 0 and 1. Binary numbers, like 110101, consist of combinations of these two digits.
Example: 110101
The rightmost digit is 20, the next is 21, then 22, and so on. The binary number 110101 is equivalent to (1 * 25) + (1 * 24) + (0 * 23) + (1 * 22) + (0 * 21) + (1 * 20) = 53 in the decimal system.
3. Octal number system (Base-8)
Octal, with a base of 8 and digits 0 to 7, is used in computing. Converting octal to decimal follows the same process as standard decimal conversion.
Example: 745
In example 745, the rightmost digit is 80, the next is 81, and the leftmost is 82. Converting this to decimal, the octal number 745 is equivalent to (7 * 82) + (4 * 81) + (5 * 80) = 485 in the decimal system.
4. Hexadecimal number system (Base-16)
Hexadecimal uses base 16 and represents numbers from 0 to 9, then employs A to F for values 10 to 15. It's a system commonly used in computing.
Example: 1A3F
In the example 1A3F, it is equivalent to (1 * 163) + (10 * 162) + (3 * 161) + (15 * 160) = 6719 in the decimal system.
Solved Examples
Q1: Find the last digit of 55552345 + 66665678
(a) 1
(b) 3
(c) 5
(d) 7
Ans: a
As the last digit depends only on last digits, consider the powers only for last digits, that is 52345 + 65678 .
As we know, any power of 5 ends only with 5 and any power of 6 ends only with 6.
The last digit of 52345 + 65678 = 5 + 6 = 11 = 1
Hence, option (A) is the correct answer.
Q2: If in a two digit number, the digit at the unit place is z and the digit at the tens place is 8, then the number is
(a) 80z + z
(b) 80 + z
(c) 8z + 8
(d) 80z + 1
Ans: (b)
Digit at unit’s place = z
The digit at ten’s place = 8
= 2-digit number = (10×8)+(1×z)
= 80 + z
Q3: How many trailing zeroes (zeroes at the end of the number) does 60! have?
(a) 14
(b) 12
(c) 10
(d) 8
Ans: (a)
Q4. How many even integers n, where 100 ≤ n ≤200 , are divisible neither by seven nor by nine
(a) 40
(b) 37
(c) 39
(d)38
Ans: (c)
1. Total even integers:
Range: 100, 102, ..., 200.
Number of even integers: (200 - 100) / 2 + 1 = 51.
2. Even numbers divisible by 7 or 9 (using inclusion-exclusion):
Divisible by 7: Even multiples of 7 are multiples of LCM(2, 7) = 14.
Multiples of 14: 14 × 8 = 112 to 14 × 14 = 196.
Count: 14 - 8 + 1 = 7.
Divisible by 9: Even multiples of 9 are multiples of LCM(2, 9) = 18.
Multiples of 18: 18 × 6 = 108 to 18 × 11 = 198.
Count: 11 - 6 + 1 = 6.
Divisible by both (7 and 9): Even multiples of LCM(7, 9) = 63.
Multiples of 126: 126 × 1 = 126.
Count: 1.
Inclusion-exclusion: 7 + 6 - 1 = 12.
3. Even numbers neither divisible by 7 nor 9:
Total even numbers: 51.
Divisible by 7 or 9: 12.
Neither: 51 - 12 = 39
|
205 videos|264 docs|136 tests
|
FAQs on Introduction: Number System - CSAT Preparation - UPSC
| 1. What are the different classifications of numbers in mathematics? |  |
| 2. What is the significance of co-prime or relatively prime numbers? |  |
| 3. How do you find the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of two numbers? |  |
| 4. What is the concept of remainders in division? |  |
| 5. How do base systems work and what are some common examples? |  |