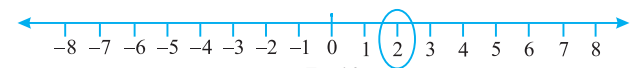Integers Class 6 Notes Maths Chapter 1
| Table of contents |

|
| Introduction |

|
| Integers: Negative and Positive |

|
| Representation of Integers on a Number Line |

|
| Ordering of Integers |

|
| Addition of Integers |

|
| Subtraction of Integers |

|
| Important Questions |

|
Introduction
Integers are all around us, even if we don't realize it! In this chapter, we'll explore the world of integers and learn how to use them to represent and solve problems in our daily lives.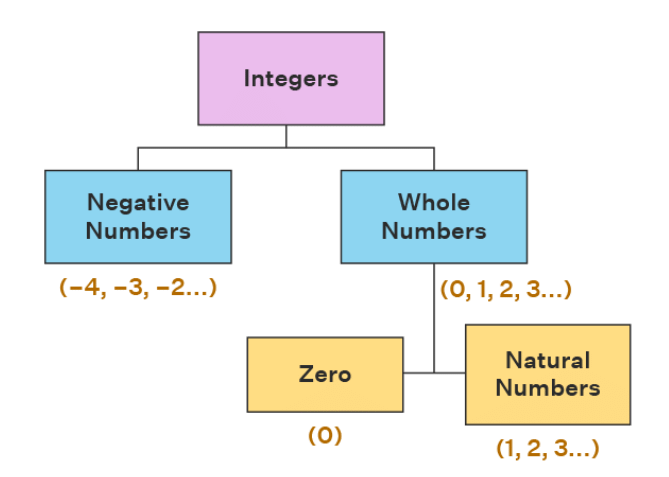 IntegersLet's say Rahul is going for a picnic with his friends. He wants to carry cupcakes with him, but he has got only 3 cupcakes, and there are 4 friends. What is he going to do now?
IntegersLet's say Rahul is going for a picnic with his friends. He wants to carry cupcakes with him, but he has got only 3 cupcakes, and there are 4 friends. What is he going to do now? So, Rahul decided to borrow one cupcake from his sister, which he would return later.
So, Rahul decided to borrow one cupcake from his sister, which he would return later.
How many cupcakes does he have now?

After borrowing one cupcake from his sister, he has got 4 cupcakes, which he would give to his four friends.
He goes for the picnic, where he gives away the 4 cupcakes to his friends.
Now, how many cupcakes are left with him?
Is your answer zero (0)?
We can say that there are no or 0 cupcakes left with him, but we also have to keep in mind that he has borrowed one cupcake from his sister.
But there is nothing behind zero. So what would he do now?
Rahul goes beyond zero. And the numbers placed behind zero where marked with a negative (-) sign.
So, in actual Rahul has (-1) cupcake, which means that 1 cupcake is borrowed and did not belong to him.
If he buys 3 more cupcakes the next day, he will have to return 1 cupcake to his sister and will be left with 2 cupcakes only.

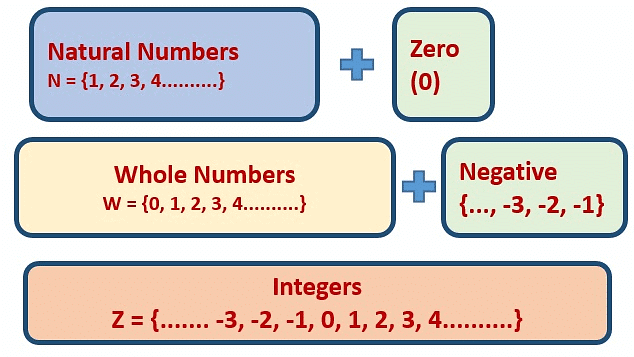
- Natural Numbers: Natural numbers are a set of positive numbers, from 1 to infinity.
Natural Numbers: 1, 2, 3, 4, 5, 6,……. - Whole Numbers: Whole numbers are also a set of positive integers, including 0, i.e. from 0 to infinity.
Whole Numbers: 0, 1, 2, 3, 4, 5, 6,……. - Negative Numbers: A negative number is a number whose value is always less than zero and it has a minus (-) sign before it.
Negative Numbers: ........, -4, -3, -2, -1
Integers
Integers is a set of whole numbers and negative of all natural numbers.
Integers: ........, -4, -3, -2, -1, 0, 1, 2, 3, 4, .....
Integers: Negative and Positive
- When we need to use numbers with a negative sign, we need to go to the left of zero on the number line. These numbers are called negative numbers.
- Examples, where these negative numbers are used: temperature scale, water level in a lake or river, level of oil tank, debit account and outstanding dues.
- The numbers -1, -2, -3, -4… which are called negative numbers, are also called negative integers.
- The number 1, 2, 3, 4 … which are called positive numbers, are also called positive integers.
- If we stand at the zero mark on the number line, we can either go left towards negative integers or right towards positive integers.

- When we move left towards zero on the number line, the value of positive integers decreases.
- When we move left further away from zero on the number line, the value of negative integers decreases.
Representation of Integers on a Number Line
- A number line is a visual representation of numbers on a straight line.
- This line is used for the comparison of numbers that are placed at equal intervals on an infinite line that extends on both sides, horizontally.
- Just like other numbers, the set of integers can also be represented on a number line.
- The collection of the numbers, that is, … -3, -2, -1, 0, 1, 2, 3, …., is called integers.
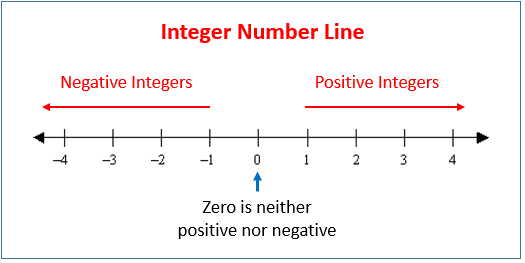
- Draw a line and mark a point as 0 on it.
- Points marked to the left (-1, -2, -3, -4, -5, -6) are called negative integers.
- Points marked to the right (1, 2, 3, 4, 5, 6) or (+1, +2, +3, +4, +5, +6) are called positive integers.
Example: Mark 2 on a number line.
In order to mark + 2 on the number line, we move 2 points to the right of zero.
3 less than 5
Ordering of Integers
Ordering of integers is stated for the series or a sequence where numbers are arranged in an order. The integers are ordered on a number line based on positive integers and negative integers.
Let us again observe the integers represented on the number line.

We know that 5 > 4 and from the number line shown above, we observe that 5 is to the right of 4.
Similarly, 4 > 0, and 4 is to the right of 0.
Now, since 0 is to the right of –3 so, 0 > – 1.
Again, – 1 is to the right of – 2 so, – 1 > – 2.
Thus, we see that on a number line, the number increases as we move to the right and decreases as we move to the left.
Therefore, – 3 < – 2, – 2 < – 1, – 1 < 0, 0 < 1, 1 < 2, 2 < 3 so on.
Hence, the collection of integers can be written as...,–5, –4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5...

Comparing Integers
- One integer can be either greater or smaller than another integer.
- Thus, to compare two integers, we use symbols greater than (>) and less than (<).
- Also, if two integers are equal to each other then we use the ‘equal to’ (=) symbol.
See the examples below:
- 0 > – 8
- 8 > – 5
- 0 < 3
- -1 > -10
- 10 < 12
- -20 < 1
- -100 < -10
- 100 > -200
From the above examples, we can observe that the more an integer is negative, the less its value is.
Q.1. Which integers lie between 0 and -3?
Solution: By the order of integers, we know that,
-3 < -2 < -1 < 0
Therefore, there are two integers between 0 and -3, they are -1 and -2.
Q.2. Which is the largest integer and smallest integer among the following?
8, 10, -12, 0, 23, 1, 3, -7, -22
Solution: Given, the integers are:
8, 10, -12, 0, 23, 1, 3, -7, -22
Smallest integer = -22
Largest integer = 23
Q.3. Gautam is at -2. In which direction and how many steps should he move to reach at – 6?
Solution: Gautam has to move 4 steps to the left of -2 to reach -6.
Q.4: Which number will we reach if we move 5 steps to the right of –3?
Solution: If we move 5 steps to the right of -3, we reach 2.
Addition of Integers
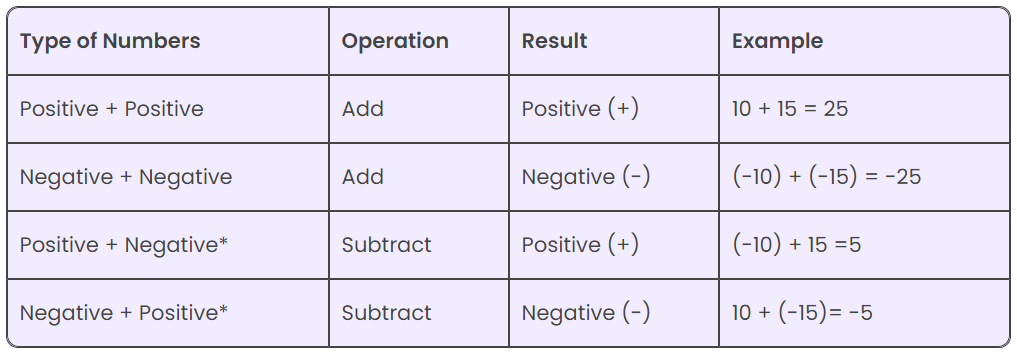
The three main possibilities in the addition of integers are:
- Addition between two positive numbers
- Addition between two negative numbers
- Addition between a positive number and a negative number
 Rules of Addition of integers
Rules of Addition of integers
- Addition between two positive numbers: When two positive integers are added, then we get an integer with a positive sign.
Example:
(+8) + (+6)= + 14
(+10) + (+15)= +25 - Addition between two negative numbers: When two negative integers are added, then we get an integer with a negative sign.
Example:
(-3) + (-5) = -8
10 + (-15) = -5 - Addition between a positive number and a negative number: When a positive integer is added to a negative integer, then we subtract them and put the sign of the greater integer. The greater integer can be decided by ignoring the signs of the integers.
Example:
(+3) + (-4) = -1;
(+5) + (-3) =2 - Additive Inverse: Numbers such as 8 and – 8, 2 and – 2, when added to each other give the sum zero. They are called additive inverse of each other.
Q.1. Add (+ 5) + (– 8)
Solution:
= (+ 5) + (– 5) + (– 3)
= 0 + (– 3) = (– 3)
Q.2. Find the sum of (– 9) + (+ 4) + (– 6) + (+ 3)
Solution: We can rearrange the numbers so that the positive integers and the negative integers are grouped together.
We have (– 9) + (+ 4) + (– 6) + (+ 3)
= (– 9) + (– 6) + (+ 4) + (+ 3)
= (– 15) + (+ 7)
= – 8
Addition of Integers on a Number Line
To add integers on a number line, just check the sign of the second number you're adding. If we add a positive number to the given integer, we move towards the right side, and if we add a negative integer to the given integer, we move towards the left side. Let us take a few examples to add integers on a number line.
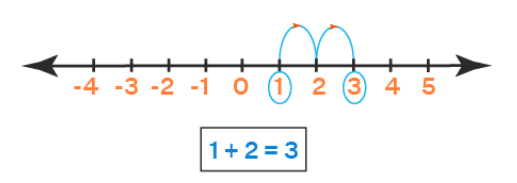
Example 1: Perform the operation 1 + 2 using a number line.
Let us look into the steps given below to understand the problem.
Step 1: Consider the first number (1) as the starting point on the number line. In order to add 1 + 2, mark 1 on the number line.
Step 2: Now, from the first number jump by the number of units equivalent to the second number towards the right. This is because the values on a number increase as we move towards the right-hand side. In this case, we are adding 1 + 2, therefore, we will move 2 steps to the right. This will bring us to number 3. So, 1 + 2 = 3.
Example 2: Perform the operation 3 + (-4) using a number line.
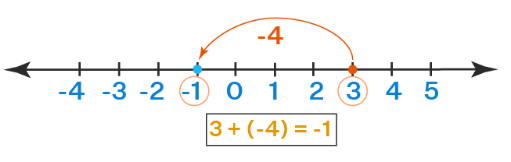
The steps remain the same as earlier except for the direction of movement as the addition operation is with a negative number. Here, we take 3 as the starting number and move 4 units towards the left on the number line since the second number is -4 which gives the result as -1.
Subtraction of Integers
- When we subtract a larger positive integer from a smaller positive integer, the difference is a negative integer.
Example: (+5)-(+8) = -3- To subtract a negative integer from any given integer, we just add the additive inverse of the negative integer to the given integer.
Example: (-5)-(-8) = +3
Thus, the subtraction of an integer is the same as the addition of its additive inverse. Both addition and subtraction of integers can be shown on a number line.
Q.1. Subtract (– 4) from (– 10)
Solution:
(– 10) – (– 4) = (– 10) + (additive inverse of – 4)
= –10 + 4 = – 6
Q.2. Subtract (+ 3) from (– 3)
(– 3) – (+ 3) = (– 3) + (additive inverse of + 3)
= (– 3) + (– 3) = – 6
Subtraction of Integers with the help of a Number Line
- To subtract integers on a number line, just check the sign of the number you're subtracting.
- To subtract a positive integer, we move towards the left on a number line, and to subtract a negative integer we move towards the right on the number line.
Example 1: Perform the operation 5 - 3 using a number line. Subtraction of Integers on a Number Line
Subtraction of Integers on a Number Line
Let us look into the steps given below to understand the problem.
Step 1: Mark the first number (5) on the number line.
Step 2: Move towards the left-hand side of the number line according to the second number given. In this case, the second number is 3, so we will move 3 units to the left as shown by the arrows. Hence, we land on 2, which is the answer.
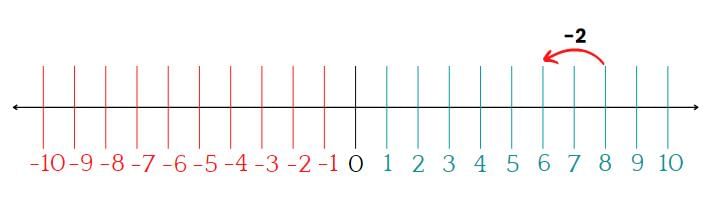
Example 2: Subtract 3 from -4 using a number line.
We will follow the steps of subtracting integers on number line to solve the problem.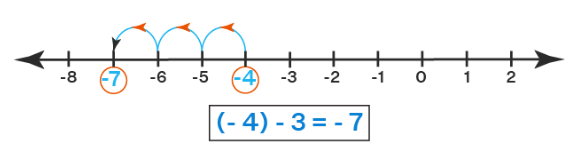
We start with the first number -4 on the number line as shown and move by the number of units equivalent to the second number that is 3 units towards the left and reach on -7. Thus, we see that the subtraction of - 4 - 3 = - 7 is shown on the number line.
Important Questions
Q1. Write all the integers between -8 and -15. (Write them in increasing order.)
Ans: The integers between –8 and –15 in increasing order are:
–14, –13, –12, –11, –10 and –9.
Q2. Find the solution of the following :(–9) + (+13)
Ans: (–9) + (+13)
= (–9) + (+9) + (+4)
= 0 + (+4) = +4
Q3. Subtract :(–20) – (–13)
Ans: (–20) – (–13)
= (–20) + (additive inverse of -13)
= (–20) + (13) = –7
Q4. Find the value of :(–7) + (–9) + 4 + 16
Ans: (–7) + (–9) + 4 + 16
= (–16) + 20
= (–16) + 16 + 4
= 0 + 4 = 4
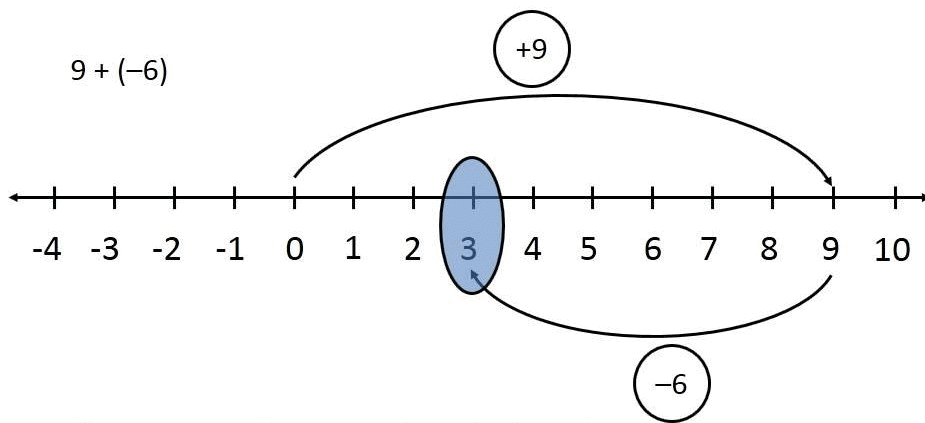
Q5. Using number line, add the following integers: 9 + (-6).
Ans: On the number line we first move 9 steps to the right from 0 reaching 9 and then we move 6 steps to the left of 9 and reach 3.
Thus, 9 + (-6) = 3
Q6. The temperature on a certain morning is -11℃ at 5 a. m. If the temperature drops 3 degree at 6 a.m. and rises 5 degree at 8 a.m. and again drops 3 degree at 9 a.m. What is the temperature at 9 a.m.?
Ans: Temperature at 5 a.m. = -11℃
Temperature decreased at 6 a.m. by 3℃ = -3
Temperature raised at 8 a.m. by 5℃ = +5
Temperature decreased at 9 a.m. by 3℃ = -3
Final temperature at 9 a.m. = (-11) + (-3) + (+5) + (-3)
= -11 – 3 + 5 – 3
= -17 + 5
= -12℃.
Q.7. What are Integers on a Number Line?
Integers on a number line are a way to represent integers visually where all the positive and negative integers including 0 are plotted. It helps us to compare integers and to perform arithmetic operations on them.
Integers on a number line are a way to represent integers visually where all the positive and negative integers including 0 are plotted. It helps us to compare integers and to perform arithmetic operations on them.
Q.8. How to Represent Integers on Number Line?
Integers are marked on a number line as follows:
- The integer 0 is marked at the center of the number line.
- All the positive integers are marked towards the right of 0 and all the negative integers are plotted towards the left of 0 on the number line.
For example, we will represent the integer 5 on the right of 0, and - 9 will be represented on the left of 0.
Q.9. How to Add and Subtract Integers on Number Line?
- To add integers, we always start with the first number and move towards the right (if positive) or left (if negative) by equivalent units of the second number.
For example, to perform 5 + (- 4), we start from 5 and move by 4 units towards the left landing at 1. - To subtract integers, we always start with the first number and move towards the left (if positive) or right (if negative) by equivalent units of the second number.
For example, to perform - 8 - (- 3), we start from - 8 and move by 3 units towards the right landing at - 5.
|
34 videos|131 docs|58 tests
|
FAQs on Integers Class 6 Notes Maths Chapter 1
| 1. What are integers and how are they categorized? |  |
| 2. How can integers be represented on a number line? |  |
| 3. How do you order integers from least to greatest? |  |
| 4. What are the rules for adding integers? |  |
| 5. How do you subtract integers? |  |