Mensuration Class 6 Notes Maths Chapter 9
| Table of contents |

|
| What is Mensuration? |

|
| Perimeter |

|
| Area |

|
| Summary |

|
What is Mensuration?
Mensuration is a part of mathematics focused on measuring geometric shapes. It involves studying different geometric forms, including their length, width, volume, and area for both 2D and 3D shapes.
When discussing plane figures, we consider their areas and boundaries, which require measures for comparison.

Some important terminologies included in this topic are covered below.
Perimeter
The perimeter is the total distance around a closed figure when you move along its boundary once. We commonly encounter the idea of perimeter in everyday life.
For Example:
- A farmer wanting to enclose his field with a fence.
- An engineer planning to build a wall around a house.
Closed figure
- A figure with no open ends is known as a closed figure.
- Figures where all sides and angles are equal are termed regular closed figures.
- The perimeter of a regular closed figure is the distance measured around the boundary when you go around it once.
- The area is the amount of surface enclosed by a closed figure.
Perimeter of a Rectangle:
= Length(l) + Breadth(b) +Length(l) + Breadth (b)= 2 (l + b)
Example 1: A rectangle has a length of 5 units and a breadth of 3 units.
Solution:
Perimeter = 2(length + breadth)
= 2(5 + 3)
= 2(8)= 16 units
Example 2: A rectangular garden has a length of 15 meters and a breadth of 7 meters. Find the perimeter of the garden.
The perimeter of a rectangle is given by the formula P = 2(l + b), where l is the length and b is the breadth.
l = 15 meters
b = 7 meters
So, the perimeter is P = 2(15 + 7)
= 2(22)= 44 meters
Perimeter of a Square:
The perimeter is the total distance around a closed shape when you walk around it once.
= s + s + s + s
= 4 x S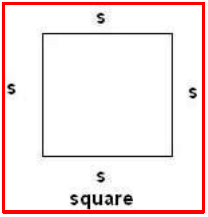
Example 1: A square has a side length of 4 units.
Perimeter = 4 * side
length = 4 * 4= 16 units
Example 2: A square photo frame has a side length of 8 centimeters. Find the perimeter of the photo frame.
The perimeter of a square is given by the formula P = 4s, where s is the side length.
s = 8 centimeters
So, the perimeter is P = 4(8)
= 32 centimeters
Perimeter of an Equilateral triangle:
A triangle with all its sides and angles equal is called an equilateral triangle.The perimeter of an equilateral triangle with the side 'a'=a+a+a =3 x a
Example 1: An equilateral triangle has a side length of 6 units.
Perimeter = 3 * side length
= 3 * 6
= 18 units
Example 2: An equilateral triangle has a side length of 10 inches. Find the perimeter of the triangle.
The perimeter of an equilateral triangle is given by the formula P = 3s, where s is the side length.
s = 10 inches
So, the perimeter is P = 3(10)= 30 inches
Area
The space enclosed by a closed figure is known as its area. To calculate the area of a closed figure using squared or graph paper, you should follow these guidelines:
- Count the fully-filled squares covered by the closed figure as one square unit or unit square each.
- Count the half-filled squares as half a square unit.
- Count the squares that are more than half-filled as one square unit.
- Ignore the squares that are filled less than half.
- Ignore parts of the area that are less than half a square.
- If exactly half a square is counted, consider its area as ½ sq unit.
For example, the area of this shape can be calculated as shown:

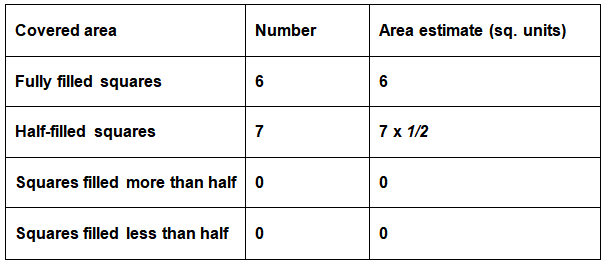
- Area covered by full squares = 6 x 1 = 6 sq. units Area covered by half squares = 7 x ½ = 7/2= 3 ½ sq. units.
- Total area of the given shape = 6 + 3 ½ sq. units Thus, the total area of the given shape = 9 ½ sq. Units.
Area of a Rectangle
The area of the rectangle can be obtained by multiplying the length by the breadth.
Area = length ( l ) × breadth ( b)
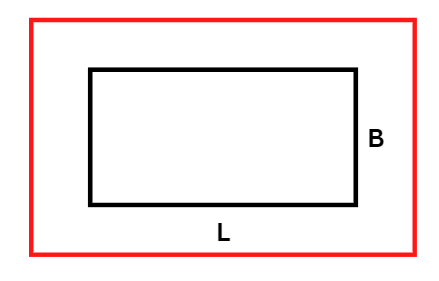
Example: Find the area of a rectangle with a length 8 units and breadth 5 units.
The formula for the area of a rectangle is
A = length × breadth
A = 8 × 5
A = 40 square units
Area of a Square
The area of the square can be obtained by multiplying side by side.
Area of a square = Side × Side =Side2=a2, where a is the length of each side.
Example: Find the area of a square with a side length of 6 units.
The formula for the area of a square is
A = side × side
A = 6 × 6
A = 36 square units
Area of a Triangle
Area of triangle = (1/2) × base × height = (1/2) × b × h
Example: Find the area of a triangle with a base of 10 units and height of 4 units.
The formula for the area of a triangle is
A = (1/2) × base × height.
A = (1/2) × 10 × 4
A = 20 square units
Summary

Mensuration is a part of mathematics focused on measuring geometric shapes. It involves studying different geometric forms, including their length, width, volume, and area for both 2D and 3D shapes.
When discussing plane figures, we consider their areas and boundaries, which require measures for comparison.
|
30 videos|120 docs|59 tests
|
FAQs on Mensuration Class 6 Notes Maths Chapter 9
| 1. What is the formula for finding the perimeter of a rectangle? |  |
| 2. How can the area of a triangle be calculated? |  |
| 3. What is the difference between perimeter and area? |  |
| 4. How can the area of a circle be calculated? |  |
| 5. What is the formula for finding the perimeter of a circle? |  |





















