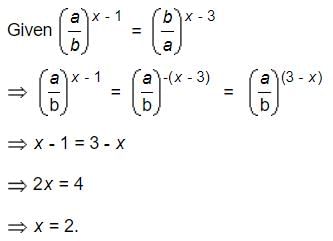Introduction: Indices and Surds | CSAT Preparation - UPSC PDF Download
| Table of contents |

|
| What are Indices? |

|
| Solved Examples on Indices |

|
| Surds |

|
| Difference between Surds and Indices |

|
| Solved Examples on Surds & Indices |

|

What are Indices?
Index (indices) in Maths is the power or exponent which is raised to a number or a variable.
- For example, in number 24, 4 is the index of 2. The plural form of index is indices. In algebra, we come across constants and variables.
- The constant is a value that cannot be changed. Whereas a variable quantity can be assigned any number or we can say its value can be changed. In algebra, we deal with indices in terms of numbers.
- A number or a variable may have an index. The index of a variable (or a constant) is a value that is raised to the power of the variable. The indices are also known as powers or exponents. It shows the number of times a given number has to be multiplied.
- It is represented in the form:
am = a x a x a x ........ x a (m times)
Here, a is the base and m is the index. - The index says that a particular number (or base) is to be multiplied by itself, the number of times equal to the index raised to it. It is a compressed method of writing big numbers and calculations.
- Example: 23 = 2 × 2 × 2 = 8
In the example, 2 is the base, and 3 is the index.
Laws of Indices
- There are some fundamental rules or laws of indices that are necessary to understand before we start dealing with indices. These laws are used while performing algebraic operations on indices and while solving the algebraic expressions, including it.
- Rule 1: If a constant or variable has index as ‘0’, then the result will be equal to one, regardless of any base value.
a0 = 1
Example: 50 = 1, 120 = 1, y0= 1 - Rule 2: If the index is a negative value, then it can be shown as the reciprocal of the positive index raised to the same variable.
a-p = 1/ap
Example: 5-1 = ⅕, 8-3=1/83 - Rule 3: To multiply two variables with the same base, we need to add its powers and raise them to that base.
ap.aq = a(p+q)
Example: 52.53 = 52+3 = 55 - Rule 4: To divide two variables with the same base, we need to subtract the power of the denominator from the power of the numerator and raise it to that base.
ap/aq = ap-q - Example: 104/102 = 104-2 = 102
Rule 5: When a variable with some index is again raised with a different index, then both the indices are multiplied together raised to the power of the same base.
(ap)q = apq
Example: (82)3 = 82.3 = 86 - Rule 6: When two variables with different bases, but the same indices are multiplied together, we have to multiply its base and raise the same index to multiplied variables.
ap.bp = (ab)p
Example: 32.52 = (3 x 5)2 = 152 - Rule 7: When two variables with different bases, but the same indices are divided, we are required to divide the bases and raise the same index to it.
ap/bp = (a/b)p
Example: 32/52 = (3/5)2 - Rule 8: An index in the form of a fraction can be represented as the radical form.
ap/q = q√ap
Example: 61/2 = √6
Let's look at some solved examples for Indices
Solved Examples on Indices
Q.1. Multiply x4y3z2 and xy5z-1
Ans:
x4y3z2 and xy5z-1
= x4.x .y3.y5.z2.z-1
= x4+1.y3+5.z2-1
= x5.y8.z
Q.2. Solve a3b2/a2b4
Ans:
a3b2/a2b4
= a3-2b2-4
= a1b-2
= a b-2
= a/b2
Q.3. Find the value of 272/3
Ans:
3√272
= 32
= 9
If  then the value of x is:
then the value of x is:
Surds
- In Mathematics, surds are the values in a square root that cannot be further simplified into whole numbers or integers. Surds are irrational numbers. The examples of surds are √2, √3, √5, etc., as these values cannot be further simplified.
- If we further simply them, we get decimal values, such as:
√2 = 1.4142135…
√3 = 1.7320508…
√5 = 2.2360679… - Surds are the square roots (√) of numbers that cannot be simplified into a whole or rational number. It cannot be accurately represented in a fraction. In other words, a surd is a root of the whole number that has an irrational value. Consider an example, √2 ≈ 1.414213. It is more accurate if we leave it as a surd √2.
Types of Surds
The different types of surds are as follows:
- Simple Surds: A surd that has only one term is called a simple surd.
Example: √2, √5, … - Pure Surds: Surds which are completely irrational.
Example: √3 - Similar Surds: The surds having the same common surds factor.
- Mixed Surds: Surds that are not completely irrational and can be expressed as a product of a rational number and an irrational number.
- Compound Surds: An expression that is the addition or subtraction of two or more surds.
- Binomial Surds: A surd that is made of two other surds.
Rules for Surds
- Rule 1: √(a × b) = √a x √b
Example: To simplify √18 = √(9 x 2) = √(32 x 2), since 9 is the greatest perfect square factor of 18.
Therefore, √18 = √(32 x 2)= √32 x √2= 3√2 - Rule 2: √(a / b) = (√a / √b)
Example: √(12 / 121) = √12 / √121 = √(22 x 3) / 11 = √22 x √3 / 11= (2√3) / 11 - Rule 3: (b / √a) x (√a x √a) = (b√a)/a
You can rationalize the denominator by multiplying the numerator and the denominator by the denominator.
Example: Rationalise 5/√7
Multiply numerator and denominator by √7 / √7 = (5/√7) x (√7/√7)= 5√7/7 - Rule 4: a√c ± b√c = (a±b)√c
Example: To simplify, 5√6 + 4√6
= 5√6 + 4√6 = (5 + 4)√6
= 9√6 - Rule 5: c/(a±b√n)
Multiply top and bottom by a±b√n
This rule enables us to rationalize the denominator.
Example: To Rationalise 3/(2+√2) = 3(2+√2) × (2−√2)/(2-√2)
=(6−3√2)/(4−2)
= (6−3√2)/2

Difference between Surds and Indices
- Surds are the root values that cannot be written as whole numbers. Indices are the power or exponent of a value. For example, for 32, 2 is the index, and 3 is the base.
- Suppose, we have a value √33. This value can be written as:
√33 = (33)½ = 33/2
Where 3/2 is the index.
As we have completed the chapter, let's look at some solved examples.
Solved Examples on Surds & Indices
Example 1: 163/2 + 16-3/2 = ?
We know, by laws of exponents,
am x an = am+n
a-m = 1/am
163/2 + 1/163/2
(161/2)3 + 1/(161/2)3
(42 x 1/2)3 + 1/(42 x 1/2)3
43 + 1/43
64 + 1/64
(64 x 64+ 1)/64
= (4096+1)/64
= 4097/64
Example 2: If (1/5 )3a = 0.008 Find the value of ( 0.25)a
(1/5 )3a = 0.008 = 8/1000 = 1/125 = (1/5 )3
Apply the Algebra Law and Solve the equation.
⇒ 3a = 3
∴ a = 1
∴ ( 0.25 )a = ( 0.25 )1 = 0.25
Example 3: Write down the conjugate of 5√3 + √2
The conjugate of 5√3 + √2 is 5√3 - √2.
Example 4: Rationalise the denominator: 1/[(8√11 )- (7√5)]
Given: 1/[(8√11 )- (7√5)]
It is known that the conjugate of (8√11 )- (7√5) is (8√11 )+(7√5)
To rationalize the denominator of the given fraction, multiply the conjugate of denominator on both numerator and denominator.
= [1/[(8√11 )- (7√5)]]× [[(8√11 )+ (7√5)]/[(8√11 )+(7√5)]]
= [(8√11 )+ (7√5)]/[(8√11 )2-(7√5)2]
= [(8√11 )+ (7√5)]/[704- 245]
= [(8√11 )+ (7√5)]/459
Example 5: Multiply √7 x √2
√7 x √2 = √(7 x 2) = √14
Example 6: Divide √10 by √5.
√10/√5 = √(10/5) = √2
Example 7: Solve √x + 2√x.
√x + 2√x = 3√x
|
207 videos|276 docs|138 tests
|
FAQs on Introduction: Indices and Surds - CSAT Preparation - UPSC
| 1. What are indices? |  |
| 2. Can you provide some examples of indices problems? |  |
| 3. What are surds? |  |
| 4. How are surds different from indices? |  |
| 5. Can you provide some examples of surds and indices problems? |  |