Composition of Functions | Mathematics (Maths) Class 12 - JEE PDF Download
Composite Functions
Let f: X → Y1 and g: Y2 → Z be two functions and the set D = {x ∈ X: f(x) ∈ Y2}. If D ≡ Ø, then the function h defined on D by h(x) = g{f(x)} is called composite function of g and f and is denoted by gof. It is also called function of a function.
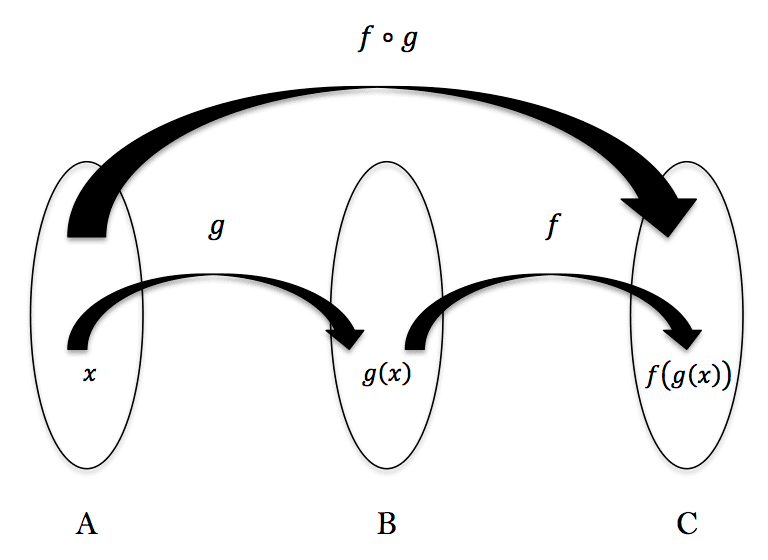
Remark: Domain of gof is D which is a subset of X (the domain of f). Range of gof is a subset of the range of g. If D = X, then f(X) ⊆ Y2.
Properties of composite functions
- The composite of functions is not commutative i.e. gof ≠ fog.
- The composite of functions is associative i.e. if f, g, h are three functions such that fo (goh) & (fog) oh are defined, then fo (goh) = (fog) oh.
Example 1. Let f(x) = ex ; R+ → R and g(x) = sin-1 x; [-1, 1] →[- π/2 , π/2]. Find domain and range of fog (x)
Solution. Domain of f(x): (0, ∞), Range of g(x): [- π/2 , π/2]
The values in range of g(x) which are accepted by f(x) are (0, π/2]
⇒ 0 < g(x) ≤ π/2 0 < sin-1 x ≤ π/2 , 0 < x ≤ 1
Hence domain of fog(x) is x ∈ (0, 1]
Example 2. Let f(x) = (x-1)/(x+1) , f2(x) = f{f(x)}, f3 (x) = f{f2(x)},.....fk + 1 (x) = f{fk(x)}. for k = 1, 2, 3,...., Find f1998 (x).
Solution.
Thus, we can see that fk(x) repeats itself at intervals of k = 4.
Hence, we have f1998(x) = f2(x) = -1/x, [∴ 1998 = 499 × 4 + 2]
Example 3. Let g : R → R be given by g(x) = 3 + 4x. If gn(x) = gogo....og(x), show that fn(x) = (4n - 1) + 4nx if g-n (x) denotes the inverse of gn (x).
Solution. Since g(x) = 3 + 4x
g2(x) = (gog) (x) = g {g (x)} = g (3 + 4x) = 3 + 4 (3 + 4x) or g2(x) = 15 + 42x = (42 – 1) + 42x
Now g3(x) = (gogog) x = g {g2 (x)} = g (15 + 42 x) = 3 + 4 (15 + 42 x) = 63 + 43 x = (43 –1) + 43x
Similarly we get gn(x) = (4n – 1) + 4nx
Now let gn (x) = y ⇒ x = g–n(y) ....(1)
∴ y = (4n – 1) + 4nx or x = (y + 1 – 4n)4–n ...(2)
From (1) and (2) we get g–n (y) = (y + 1 – 4n) 4–n.
Hence g–n (x) = (x + 1 – 4n) 4–n
Example 4. If f(x) = If f(x) = | |x – 3| – 2 | ; 0 ≤ x ≤ 4 and g(x) = 4 – |2 – x| ; –1 ≤ x ≤ 3 then find fog(x).
Solution.
Example 5. Prove that f(n) = 1 - n is the only integer valued function defined on integers such that
(i) f(f(n)) = n for all n ε Z and
(ii) f(f(n + 2) + 2) = n for all n ε Z and
(iii) f(0) = 1.
Solution. The function f(n) = 1 - n clearly satisfies conditions (i), (ii) and (iii). Conversely, suppose a function
f: Z → Z satisfies (i), (ii) and (iii). Applying f to (ii) we get, f(f(f(n + 2) + 2))) = f(n) and this gives because of (i), f(n + 2) + 2 = f(n), ........(1)
for all n ε Z. Now using (1) it is easy to prove by induction on n that for all n ε Z,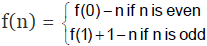
Also by (iii), f(0) = 1. Hence by (i), f(1) = 0. Hence f(n) = 1 - n for all n ε Z.
General Definition
- Identity function: A function f ; A → defined by f(x) = x ∀ x ∈ A is called the identity of A & denoted by IA.
Ex: f : R+ → R+ ; f(x) = eℓnx and f : R → R ; f(x) = ℓn ex
Every Identity function is a bijection. - Constant function: A function f: A → B is said to be constant function. If every element of set A has the same functional image in set B i.e. f: A → B ; f(x) = c ∀ x ε A & c ε B is called constant function.
- Homogeneous function: A function is said to be homogeneous w.r.t. any set of variables when each of its term is of the same degree w.r.t. those variables.
- Bounded Function: A function y = f(x) is said to be bounded if it can be express is the form of
a ≤ f(x) ≤ b where a and b are finite quantities.
Example: -1 ≤ sin x ≤ 1 ; 0 ≤ {x} < 1 ; -1 ≤ sgn (x) ≤ 1 but ex is not bounded.
Any function having singleton range like constant function. - Implicit function & Explicit function: If y has been expressed entirely in terms of `x' then it is called an explicit function.
If x & y are written together in the form of an equation then it is known as implicit equation corresponding to each implicit equation there can be one, two or more explicit function satisfying it
Example:
y = x3 + 4x2 + 5x → Explicit function
x + y = 1 → Implicit equation
y = 1 - x → Explicit function - Even & Odd Functions
Function must be defined in symmetric interval [-x, x]
If f (-x) = f (x) for all x in the domain of `f' then f is said to be an even function.
e.g. f (x) = cos x; g (x) = x² + 3.
If f (-x) = -f (x) for all x in the domain of `f' then f is said to be an odd function.
e.g. f (x) = sin x ; g (x) = x3 + x.
Remark
- f (x) - f (-x) = 0 ⇒ f (x) is even & f (x) + f (-x) = 0 ⇒ f (x) is odd.
- A function may be neither even nor odd.
- Inverse of an even function is not defined.
- Every even function is symmetric about the y-axis & every odd function is symmetric about the origin.
- A function (whose domain is symmetric about origin) can be expressed as a sum of an even & an odd function. e.g.
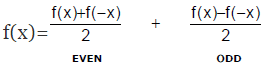
- The only function which is defined on the entire number line & is even and odd at the same time is f(x) = 0.
- If f and g both are even or both are odd then the function f.g will be even but if any one of them is odd and other even then f.g will be odd.
Example 6. Which of the following functions is odd ?
(a) sgn x + x2000
(b) | x | - tan x
(c) x3 cot x
(d) cosec x55
Solution.
Let’s name the function of the parts (A), (B), (C) and (D) as f(x), g(x), h(x) & f(x) respectively. Now
(a) f(–x) = sgn (–x) + (–x)2000 = –sgn x + x2000 ≠ f(x) & ≠ –f(x) ∴ f is neither even nor odd.
(b) g(–x) = |–x| – tan (–x) = |x| + tan x ∴ g is neither even nor odd.
(c) h(–x) = (–x)3 cot (–x) = –x3 (–cot x) = x3 cot x = h(x) ∴ h is an even function
(d) f(–x) = cosec (–x)55 = cosec (–x55) = –cosec x55 = – f(x) ∴ f is an odd function.
Alternatively
(a) f(x) = sgn (x) + x2000 = O + E = neither E nor O
(b) g(x) = E – O = Neither E nor O
(c) h(x) = O × O = E (D) f(–x) = O o O = O
(d) is the correct option
Example 7. 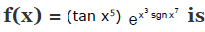
(a) An even function
(b) An odd function
(c) Neither even nor odd function
(d) None of these
Solution.
= O × eO × O = O × eE = O × E = O
Example 8. Let f: [-2, 2] → R be a function if f(x) =
so that
(i) f is an odd function
(ii) f is an even function (where [*] denotes the greatest integer function)
Solution.
(i) If f is an odd function then f(x) = –f (–x)
(ii) If f is an even function
Example 9. Let f(x) = ex + sin x be defined on the interval [-4, 0]. Find the odd and even extension of f(x) in the interval [-4, 4].
Solution.
Odd Extension: Let g0 be the odd extension of f(x), then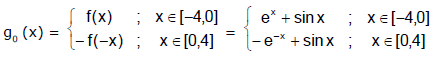
Even Extension: Let ge be the odd extension of f(x), then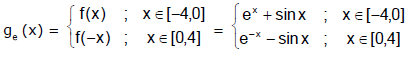
|
223 videos|377 docs|167 tests
|
FAQs on Composition of Functions - Mathematics (Maths) Class 12 - JEE
| 1. What is a composite function? |  |
| 2. How do you find the composite of two functions? |  |
| 3. What is the notation for composite functions? |  |
| 4. How can composite functions be used in real-life applications? |  |
| 5. Can you have a composite function of more than two functions? |  |

















