Integration by Substitution & Trigonometric Identities | Mathematics (Maths) Class 12 - JEE PDF Download
1. Integration by Substitution
Let g be a function whose range is an interval l, and let f be a function that is continuous on l. If g is differentiable on its domain and F is an antiderivative of f on l, then  f(g(x))g'(x) dx = F(g(x)) + C.
f(g(x))g'(x) dx = F(g(x)) + C.
If u = g(x), then du = g'(x) and  f(u) du = F(u) + C .
f(u) du = F(u) + C .
Guidelines for making a change of variable
1. Choose a substitution u = g(x). Usually, it is best to choose the inner part of a composite function, such as a quantity raised to a power.
2. Compute du = g'(x) dx.
3. Rewrite the integral in terms of the variable u.
4. Evaluate the resulting integral in terms of u.
5. Replace u by g(x) to obtain an antiderivative in terms of x.
The General Poser Rule for Integration
If g is a differentiable function of x, then 
Rationalizing Substitutions
Some irrational functions can be changed into rational functions by means of appropriate substitutions.
 |
Download the notes
Integration by Substitution & Trigonometric Identities
|
Download as PDF |
In particular, when an integrand contains an expression of the form  then the substitution u =
then the substitution u =  may be effective.
may be effective.
Some Standard Substitutions

2. Integration Using Trigonometric Identities
In the integration of a function, if the integrand involves any kind of trigonometric function, then we use trigonometric identities to simplify the function that can be easily integrated.
Few of the trigonometric identities are as follows:
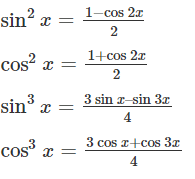
All these identities simplify integrand, that can be easily found out.
Solved Examples:
Ex.1 Evaluate  (x2 +1)2 (2x) dx .
(x2 +1)2 (2x) dx .
Sol. Letting g(x) = x2 + 1, we obtain g'(x) = 2x and f(g(x)) = [g(x)]2.
From this, we can recognize that the integrand and follows the f(g(x)) g'(x) pattern. Thus, we can write 
Ex.2 Evaluate 
Sol. 
Ex.3 Evaluate 
Sol.
Let u = x4 + 2 ⇒ du = 4x3 dx


Ex.4 Evaluate 
Sol.
Let u = x3 – 2. Then du = 3x2 dx. so by substitution :


Ex.5 Evaluate 
Sol. Let u =  . Then u2 = x + 4, so x = u2 –4 and dx = 2u du.
. Then u2 = x + 4, so x = u2 –4 and dx = 2u du.
Therefore 



Ex.6 Evaluate 
Sol. Rewrite the integrand as follows :

 = – ln (e-x + 1) + c (∴ e-x + 1 > 0)
= – ln (e-x + 1) + c (∴ e-x + 1 > 0)
Ex.7 Evaluate  sec x dx
sec x dx
Sol. Multiply the integrand sec x by sec x + tan x and divide by the same quantity :
Ex.8 Evaluate  cos x (4 - sin2 x) dx
cos x (4 - sin2 x) dx
Sol. Put sin x = t so that cos x dx = dt. Then the given integral = 


Ex.9 Integrate
(i) 
(ii) 
Sol.

Ex.10 Integrate
(i) 
(ii) 
Sol.

Ex.11 Integrate
(i) 
(ii) 
Sol.

Ex.12 Integrate 
Sol.

Ex.13 Integrate cos5x.
Sol.

 [put sin x = t ⇒ cos x dx = dt]
[put sin x = t ⇒ cos x dx = dt]


Ex.14 Evaluate 
Sol.






Ex.15 Integrate 1/(sin3 x cos5x).
Sol. Here the integrand is sin–3 x cos–5x. It is of type sinm x cosn x,where m + n = –3 –5 = –8 i.e., –ve even integer


Now put tan x = t so that sec2 x dx = dt


Ex.16 Integrate 
Sol. Here the integrand is of the type cosm x sinnx. We have m = –3/2, n = – 5/2, m + n = – 4 i.e., and even negative integer.



 ,putting tan x = t and sec2x dx = dt
,putting tan x = t and sec2x dx = dt


Ex.17 Evaluate 
Sol.
Put x – β = y ⇒ dx = dy
Given integral





Now put sinθ + cosθ tan y = z2 ⇒ cosq sec2 y dy = 2z dz



Ex.18 Evaluate  dx
dx
Sol.





|
204 videos|290 docs|139 tests
|
FAQs on Integration by Substitution & Trigonometric Identities - Mathematics (Maths) Class 12 - JEE
| 1. What is integration by substitution? |  |
| 2. How do you perform integration by substitution? |  |
| 3. What are trigonometric identities used for in integration? |  |
| 4. How can trigonometric identities be applied in integration? |  |
| 5. Can integration by substitution and trigonometric identities be used together? |  |
























