Product of Four Vectors | Mathematics (Maths) for JEE Main & Advanced PDF Download
Product of Four Vectors
(a) Scalar Product of Four Vectors: The products already considered are usually sufficient for practical applications. But we occasionally meet with products of four vectors of the following types. Consider the scalar product of This is a number easily expressible in terms of the scalar products of the individual vectors. For, in virtue of the fact that in a scalar triple product the dot and cross may be interchanged, we may write
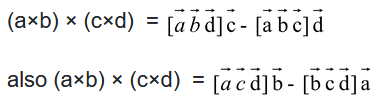
Writing this result in the form of a determinant,
we have
(b) Vector Product of Four Vectors:
Consider next the vector product of This is a vector at right angles to
and therefore coplanar with
Similarly it is coplanar with
It must therefore be parallel to the line of intersection of a plane parallel to
with another parallel to
To express the product in in terms of
regard it as the vector triple product of
and
Similarly, regarding it as the vector product of we may write it
Equating these two expressions we have a relation between the four vectors
...(3)
Example: Show that ,
Sol.
Example: Show that
Sol:
Vector Equations
Example: Solve the equation
Sol. From the vector product of each member with a, and obtain
Example: Solve the simultaneous equations
Sol. Multiply the first vectorially by
which is of the same form as the equation in the preceding example.
Thus
Substitution of this value in the first equation gives
Example:
Sol. Multiply scalarly by
Example: then prove that
Sol.
...(1)
Solving (2) and simultaneously we get the desired result.
Example: Solve the vector equation in
Sol. Taking dot with a = ...(1)
Taking cross with a = ...(2)
Example: Express a vector as a linear combination of a vector
and another perpendicular to A and coplanar with
and
.
Sol. is a vector perpendicular to
and coplanar with
and
.
Hence let,
...(1)
taking dot with
again taking cross with
|
172 videos|503 docs|154 tests
|
FAQs on Product of Four Vectors - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the formula for finding the product of four vectors? |  |
| 2. Can the product of four vectors be negative? |  |
| 3. How is the product of four vectors used in physics and engineering? |  |
| 4. What is the significance of the product of four vectors in mathematical calculations? |  |
| 5. How do you interpret the result of the product of four vectors? |  |






















