Binomial Distribution | Mathematics (Maths) Class 12 - JEE PDF Download
Binomial Probability Distribution
Suppose that we have an experiment such as tossing a coin or die repeatedly or choosing a marble from an urn repeatedly. Each toss or selection is called a trial. In any single trial there will be a probability associated with a particular event such as head on the coin, 4 on the die, or selection of a red marble. In some cases this probability will not change from one trial to the next (as in tossing a coin or die.) Such trials are then said to be independent and are often called Bernoulli trials after James Bernoulli who investigated them at the end of the seventeenth century.
Let p be the probability that an event will happen in any single Bernoulli trial (called the probability of success). Then q = 1 - p is the probability that the event will fail to happen in any single trial (called the probability of failure). The probability that the event will happen exactly x times in n trials (i.e., n successes and n - x failures will occur) is given by the probability function.
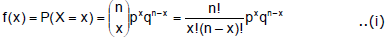
where the random variable X denotes the number of successes in n trials and x = 0, 1, ........n.
Example : The probability of getting exactly 2 heads in 6 tosses of a fair coin is
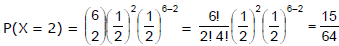
The discrete probability function (i) is often called the binomial distribution since for x = 0, 1, 2, .........n, it corresponds to successive terms in the binomial expansion
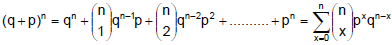
The special case of a binomial distribution with n = 1 is also called the Bernoulli distribution.
Ex.1 If a fair coin is tossed 10 times, find the probability of
(i) exactly six heads
(ii) atleast six heads
(iii) atmost six heads
Sol. The repeated tosses of a coin are Bernoulli trials. Let X denotes the number of heads in an experiment of 10 trials. Clearly, X has the binomial distribution with n = 10 and p = 1/2
Therefore P(X = x) = nCxqn–x px, x = 0, 1, 2, ........n
Here n = 10, p =1/2, q=1=1-p = 1/2.
Therefore P(X = x) =
(ii) P (atleast six heads) = P (X ≥ 6) = P (X = 6) + P (X = 7) + P(X = 8) + P (X = 9) + P(X = 10)
(iii) P (at most six heads) = P (X ≤ 6)
= P(X = 0) + P(x = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)
Ex.2 A coin is tossed 7 times. Each time a man calls head. The probability that he wins the toss on more than three occasions is
Sol. The man has to win at least 4 times then required probability
Ex.3 A man takes a step forward with probability 0.4 and backward with probability 0.6. Find the probability that at the end of eleven steps he is one step away from the starting point.
Sol. Since the man is one step away from starting point mean that either
(i) man has taken 6 steps forward and 5 steps backward.
(ii) man has taken 5 steps forward and 6 steps backward.
Taking, movement 1 step forward as success and 1 step backward as failure.
p = Probability of success = 0.4 and q = Probability of failure = 0.6
Required Probability = P [X = 6 or X = 5] = P [X = 6] + P(X = 5) = 11C6p6 q5 +11 C5p5 q6
Hence the required probability = 0.37
|
204 videos|290 docs|139 tests
|
FAQs on Binomial Distribution - Mathematics (Maths) Class 12 - JEE
| 1. What is the binomial distribution? |  |
| 2. How is the binomial distribution different from other probability distributions? |  |
| 3. How can the binomial distribution be applied in real-life situations? |  |
| 4. What are the key parameters of the binomial distribution? |  |
| 5. How is the binomial distribution calculated? |  |


























