Electric Field & Electric Field Lines | Physics Class 12 - NEET PDF Download
Electric Field
- When a charged particle is far away from another particle, they don't directly interact. Instead, the first charged particle creates something called an electric field around it.
- This electric field is like an invisible force that can affect other charges placed in that space. The area where the electric effects of a charge can be felt is called its electric field.
- We can describe the electric field at a point using either a vector function called 'electric field strength' (E) or a scalar function called 'electric potential' (V). You can also imagine the electric field using 'lines of force' on a graph. The electric field travels through space at the speed of light.
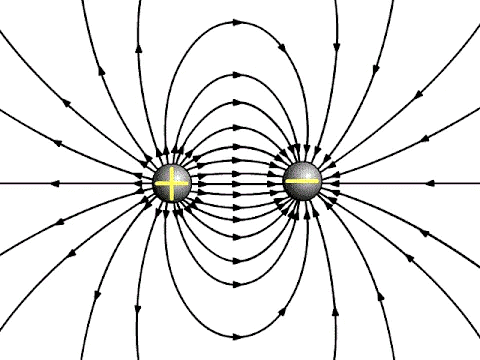 Electric field
Electric field
Strength of an Electric Field
- Similar to gravity, the electric field strength (or simply electric field) at a specific point in an electric field is defined as the force experienced by a small positive charge divided by that charge.
- If a tiny test charge (denoted as q₀) experiences an electrostatic force (F), the electric field strength (E) at that point is defined as E = F/q₀. We use a limit as q₀ approaches zero to make sure that its electric field doesn't affect the electric field of the source charge.
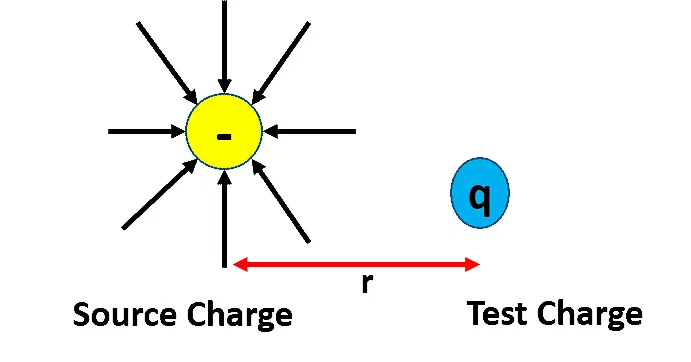 Electric field strength
Electric field strength - The unit and dimensions for the Electric Field would be Newton/Coulomb and [M1 L1 T-3A-1] respectively.
- The electric field is the property of its source. The presence of a test charge is not necessary for the Electric field (due to the source charge) to exist. It exists with or without the test charge. The test charge is used to detect and measure the Electric field due to the source charge.
- The electric field is a vector, meaning it has both magnitude and direction. Its direction is the same as the force on a positive test charge.
- Understanding the electric field involves two main ideas: first, a set of charges creates an electric field, and second, this electric field exerts a force on any charge present in it.
The Direction of Electric Field
- When there's an electric field with strength E at a particular point, it causes an electrostatic force on a positive charge q to be qE in the same direction as the field, and on a negative charge -q, the force is qE but in the opposite direction to the field.
- The direction of the electric field is radially outwards for a positive charge and is radially inwards for a negative charge, based on the direction of the electrostatic force on the ‘positive test charge’ as shown in the animations below.
- Usually, we use a positive test charge to observe the electric field. If the source charge is positive, it will push away the positive test charge, and if the source charge is negative, it will pull the positive test charge. This electric field can be seen in space.
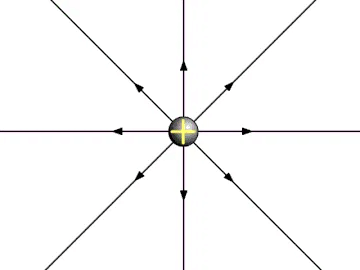 Electric field due to a Positive Charge
Electric field due to a Positive Charge 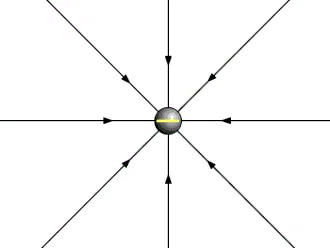 Electric field due to a Negative Charge
Electric field due to a Negative Charge
Note:
1. It is important to note that with every charged particle, there is an electric field associated which extends up to infinity.2. No charged particle experiences force due to its own electric field.
Electric Field Due to a Point Charge
Suppose the point charge +Q is located at A, where OA = r1. To calculate the electric field intensity (E) at B, where OB = r2.
 Electric field due to Point Charge
Electric field due to Point Charge

Therefore,
Electric field, E=
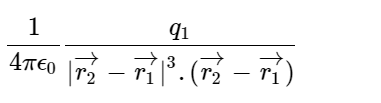
Electric Field Due to a System of Point Charges
The electric field intensity at any point due to a system or group of charges is equal to the vector sum of electric field intensities due to individual charges at the same point.
Now, we would do the vector sum of electric field intensities:
E= E1+E2+E3+......+En
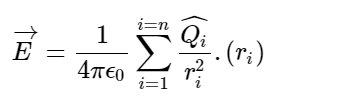 Here, ri is the distance of the point P from the ith charge Qi. ri cap is a unit vector directed from Qi to point P. Let’s say charge Q1, Q2...Qn are placed in a vacuum at positions r₁, r₂,....,rₙ respectively.
Here, ri is the distance of the point P from the ith charge Qi. ri cap is a unit vector directed from Qi to point P. Let’s say charge Q1, Q2...Qn are placed in a vacuum at positions r₁, r₂,....,rₙ respectively.
The net forces at P are the vector sum of forces due to individual charges, given by,
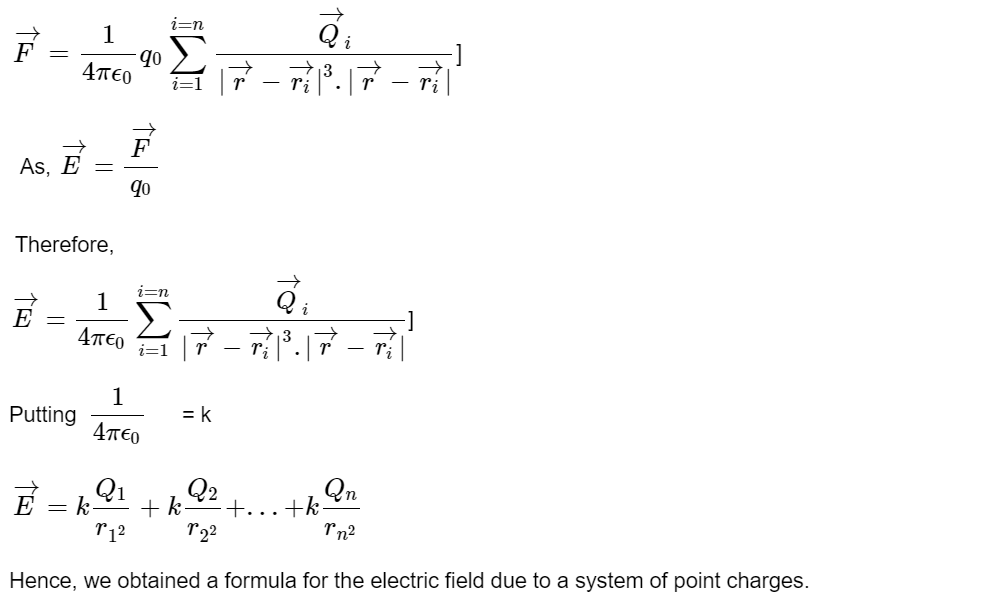
Electric Field Due to Line Charge Distribution
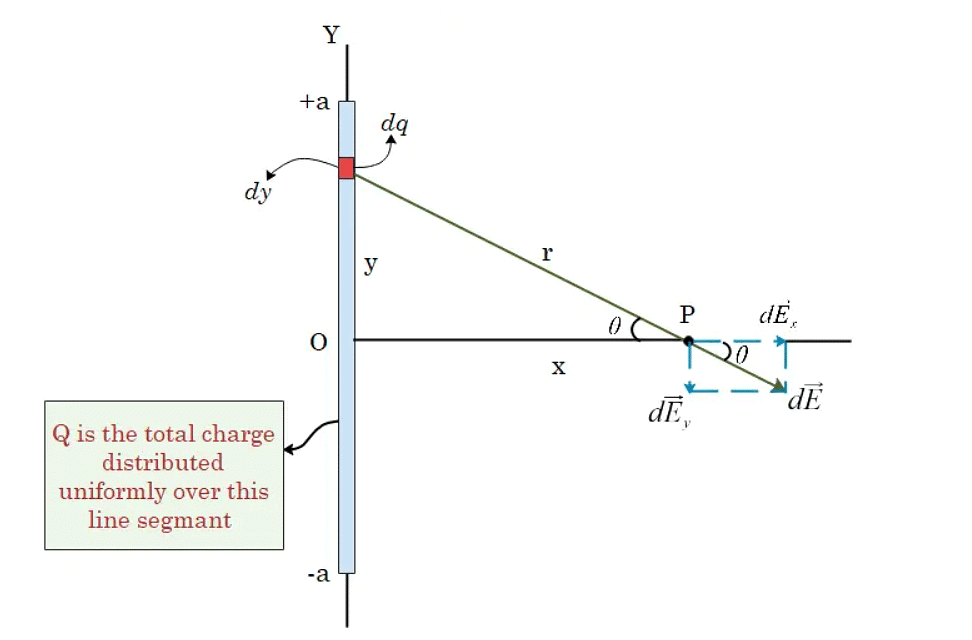
Positive charge q is distributed uniformly along a line with length 2a, lying along the y-axis between y=-a and y=+a. We are here interested in finding the electric field at point P on the x-axis.
λ=charge per unit length= q/2a
dq=λdy
 Electric field due to Line Charge Density
Electric field due to Line Charge Density
Here it is important to note that the x-axis is the perpendicular bisector of our line segment. So, our point P is at a distance x from the midpoint O of the charged line segment.
The distance r from the segment at height y to the field point P is: r=√x2+y2
So, the magnitude of the field at point P due to the segment of height y is
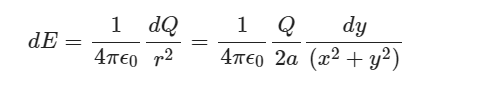
From the figure given above, we can see the x and y components of this field. Here component dEx is perpendicular to the charged line segment and dEy is parallel to it. On resolving dE into x and y components, we get
dEx=dEcosθ
dEy=−dEsinθ
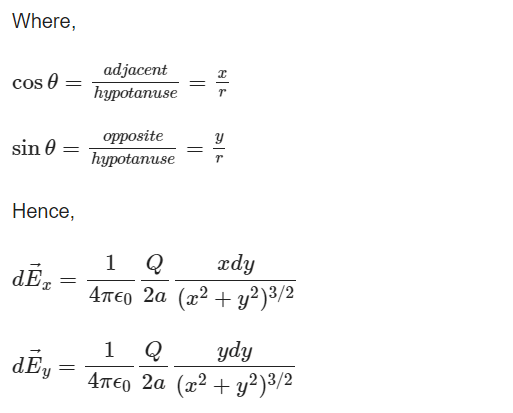 From the symmetry of the configuration, the component of dE parallel to the line charge distribution is zero. When a positive test charge is placed at P, the upper half of the charge line applies force on it along the downward direction, while the lower half applies a force of equal magnitude in an upward direction. This, the top and lower parts of the segment contribute equally to the total field at P, according to symmetry.
From the symmetry of the configuration, the component of dE parallel to the line charge distribution is zero. When a positive test charge is placed at P, the upper half of the charge line applies force on it along the downward direction, while the lower half applies a force of equal magnitude in an upward direction. This, the top and lower parts of the segment contribute equally to the total field at P, according to symmetry.

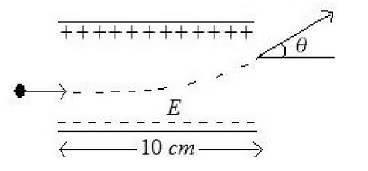
Q1: A uniform electric field of 10 N/C is created between two parallel charged plates (as shown in figure). An electron enters the field symmetrically between the plates with a kinetic energy 0.5 eV. The length of each plate is 10 cm. The angle (θ) of deviation of the path of electron as it comes out of the field is (in degree).
 Ans: 45
Ans: 45
Sol:
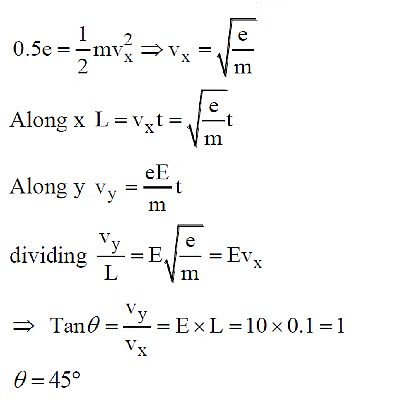
Q2: A point charge of 10 μC is placed at the origin. At what location on the X-axis should a point charge of 40pC be placed so that the net electric field is zero at x = 2 cm on the X-axis ? [JEE Main 2023]
(a) x = 6 cm
(b) x = 4 cm
(c) x = 8 cm
(d) x = -4 cm
Ans: (a)
Sol:
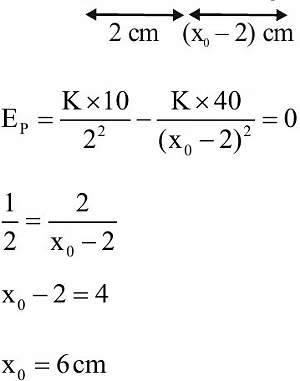
Q3: A thin infinite sheet charge and an infinite line charge of respective charge densities +σ and +λ are placed parallel at 5 m distance from each other. Points P and Q are at 3/π m and 4/π m perpendicular distances from line charge towards sheet charge, respectively Ep and Eq are the magnitudes of resultant electric field intensities at point P and Q respectively. If 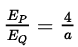 for 2|σ| = |λ|, then the value of a is _____. [JEE Main 2023]
for 2|σ| = |λ|, then the value of a is _____. [JEE Main 2023]
Ans: 6
Sol: Let's consider the following diagram:
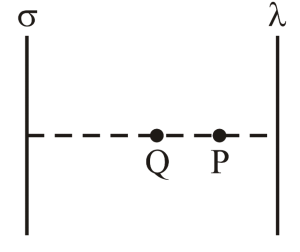
The formula to calculate the electric field due to an infinitely long charged sheet is given by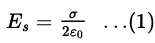
The formula to calculate the electric field due to an infinitely long line charge is given by 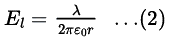
Using equations (1) and (2), the electric field at can be calculated as follows:
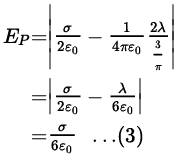
Similarly, the electric field at is given by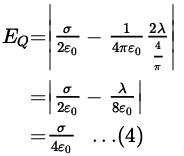
Divide equation (3) by equation (4) to obtain the required ratio.
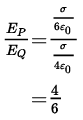
Hence, a = 6.
Physical Significance of Electric Field
The physical significance of electric field is that we can readily calculate the magnitude and direction of force experienced by any charge q0 placed at a point by knowing the electric field intensity at that point.
Electric Field Lines
Electric field lines are an imaginary tool used to visualize the electric field around a charged object.
- These lines help us understand the direction and strength of the electric field. Whenever a charged particle enters this electric field, it experiences an electrostatic force expressed by Coulomb's law.
- If the source charge is positive, then the lines are radially outwards and if the source charge is negative then the lines are radially inwards. These are not physical lines in the space, these are imaginary lines called Electric Fields lines.
Q3: Why have we defined the concept of the electric field? Is it really necessary? If eventually, we are measuring the electrostatic force, why can’t we do it directly using Coulomb’s Force?
Sol: The concept of electric field helps us understand the electrical environment around charged objects. It's not always necessary, but it becomes important when we deal with moving charges and electromagnetic waves. When charges are in motion, there is a delay between the cause and effect of their interactions, which can only be explained through the concept of the electric field. Electric and magnetic fields are considered real and physical entities that can transport energy and have their own set of laws. The concept of the electric field is now central in physics.
Properties of Electric Field Lines
Electric field lines have several important properties:
- Field lines start with positive charges and end with negative charges. If there is a single charge, they may start or end at infinity.
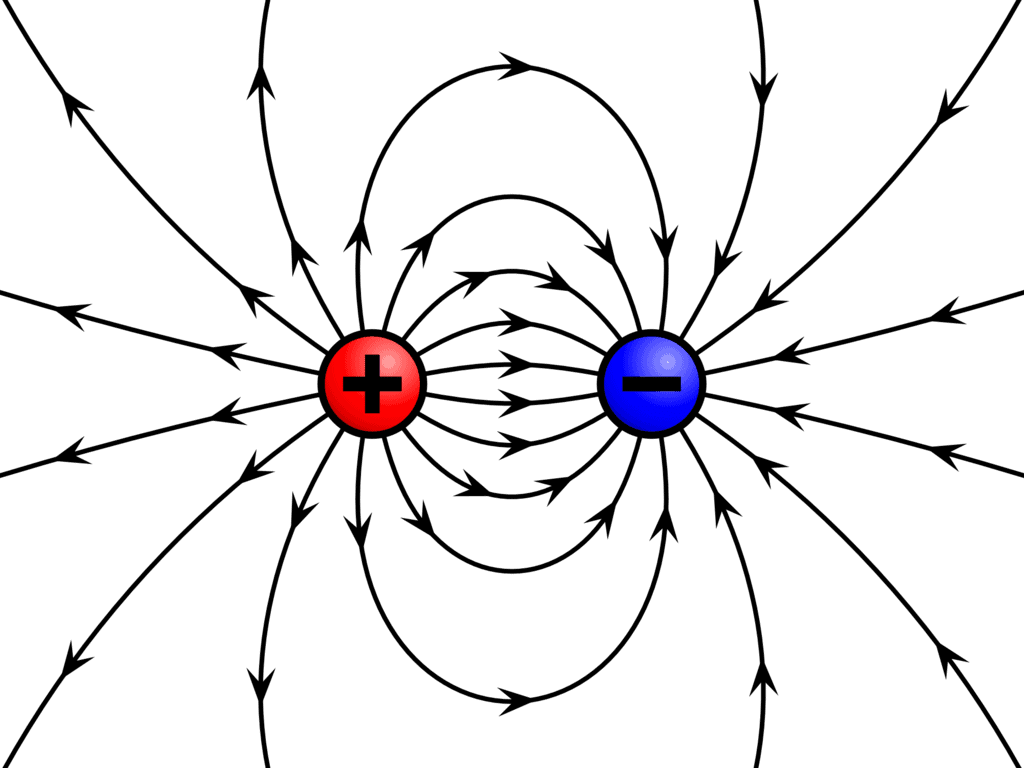 Field lines diverge from positive charges and converge in negative charges
Field lines diverge from positive charges and converge in negative charges - In a charge-free region, electric field lines can be taken to be continuous curves without any breaks.
- Tangent drawn to an electric field line represents the direction of the electric field at that point.
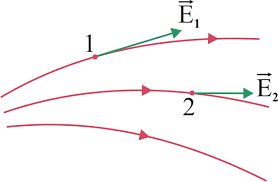 Direction of Electric Field
Direction of Electric Field - Two field lines can never cross each other. (If they did, the field at the point of intersection would not have a unique direction, which is absurd.)
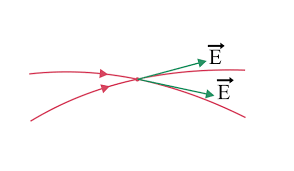 They never cross each other
They never cross each other - Electrostatic field lines do not form any closed loops. This follows from the conservative nature of the electric field.
 Electrostatic field lines do not form any closed loops
Electrostatic field lines do not form any closed loops - The number of field lines per unit area passing through a small cross-sectional area perpendicular to the electric field is called as density of field lines.
- Relative Density of Electric Field Lines represents the magnitude of Electric Field intensity 'E', which is strong near the charge, as the density of field lines is more near the charge and the lines are closer.
- Away from the charge, the field gets weaker and the density of field lines is less, resulting in well-separated lines. Some may draw more lines but the number of lines is not important. It is the relative density of lines in different regions that is important.
Electric field lines of +2Q charge are twice in number than that of +Q. So, irrespective of the number of lines in each representation, the ratio must be maintained to 2.
The relative density of field lines is inversely proportional to the square of the distance. Mathematically, the number of lines per unit area at distance r > number of lines per unit area at distance 2r > the number of lines per unit area at a distance 3r measured from S.
Relative density of field lines at distance r/Relative density of field lines at distance 2r = 4/1
Similarly, Relative density of field lines at distance 2r/Relative density of field lines at distance 3r = 9/4
Drawing Electric Field Lines
Electric field lines are a way of pictorially mapping the electric field around a configuration of charges.
- An electric field line is, in general, a curve drawn in such a way that the tangent to it at each point is in the direction of the net field at that point.
- An arrow on the curve is necessary to specify the direction of the electric field from the two possible directions indicated by a tangent to the curve. A field line is a space curve, i.e., a curve in three dimensions.
Concept of Superposition of Electric Fields
- If we are dealing with many charges (let’s assume n) then the electric field at a point p is the vector sum
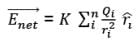
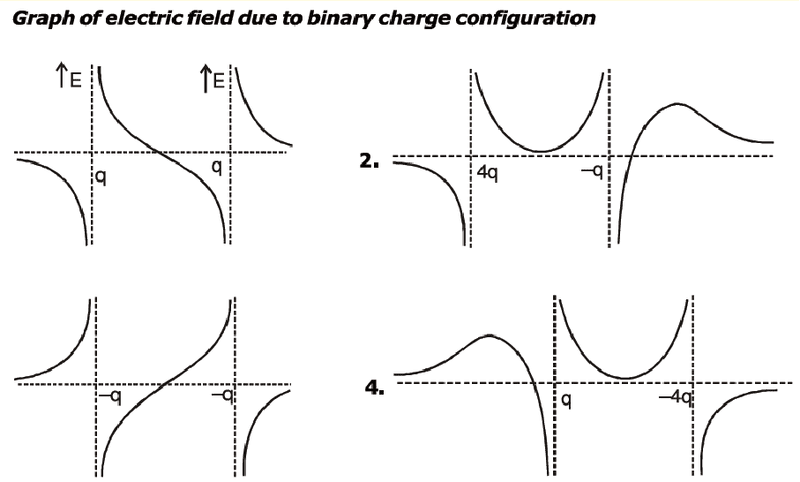
- Where ri is the is the distance from the ith source charge Qi, to the point P and
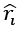 is a unit vector directed from Qi toward P. If some more charges are added, more terms are added to the summation.
is a unit vector directed from Qi toward P. If some more charges are added, more terms are added to the summation. - However, there is no change to the terms that were already there, provided that the original charges do not move. If we know the electric fields generated by two different sets of charges separately, the electric field generated by both together is simply the vector sum of the two separate fields.
- The two fields, which each occupy three-dimensional space, are superimposed on one another. Because it has this property, the electric field is said to satisfy the principle of superposition.
Graph of Electric Field Due to Binary Charge
(a) Electric field versus q for a positive point charge kept at the origin. Note that the electric field at positive q is positive because it is in a positive direction. At negative q it is negative because it is in a negative direction.
(b) Electric field versus q for a negative point charge kept at the origin. Note that the electric field at positive q is negative because it is in the negative direction. At negative q it is positive because it is in a positive direction.
Q4: Two charged particles lie along the x-axis as shown in the figure. The particle with charge q2 = +8μC is at x = 6.00 m, and the particle with charge q1 = + 2μC is at the origin. Locate the point where the resultant electric field is zero.
Sol:
Before calculating, let us physically see the location of the point where the electric field can be zero. At points other than the x-axis, say above the x-axis, both the charges will have a component of the electric field in the positive direction. This y component of the electric field does not cancel out. So the net electric field at that point will not be zero. The same statement also holds for points that are not in xy -plane.
On the x-axis also we can see that on the points beyond x = 6 m and points on the negative x-axis, both the electric fields will be in the same direction. So the net electric field cannot be zero. At some point between the two charges, the electric field due to both of them will be in opposite directions. So the electric field will be zero at a point between x = 0 and x = 6m.
Let the x coordinate of neutral point (E = 0) be x,
Therefore,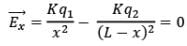
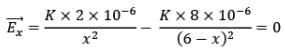
By solving the above equation for x, we get x = 2m.
Hence, at x = 2 between these two charged particles, there exists a point where net electric field due is zero i.e. neutral point.
Frequently Asked Questions (FAQs)
1. What is an electric field?
Ans. An electric field refers to the region around an electrically charged object or particle where it exerts a force on other charged objects or particles. It is a vector quantity and is represented by an arrow pointing in the direction of the force that a positive test charge would experience if placed in the field.
2. How is the direction of an electric field determined?
Ans. The direction of an electric field is determined by the direction of the force that a positive test charge would experience if placed in the field. The direction of the electric field lines also follows this direction, pointing away from positive charges and towards negative charges.
3. How is the electric field strength due to a point charge calculated?
Ans. The electric field strength due to a point charge can be calculated using the formula E=kq/r^2, where E is the electric field strength, k is Coulomb's constant (9 x 10^9 Nm^2/C^2), q is the charge of the point charge, and r is the distance between the point charge and the location at which the electric field strength is being calculated.
4. What are electric field lines?
Ans. Electric field lines are visual representations of the electric field around a charged object or particle. They are drawn as continuous lines that start from positive charges and end at negative charges, and the density of the lines indicates the strength of the electric field at different points in space.
5. How is the concept of superposition used to calculate the electric field due to multiple charges?
Ans. The concept of superposition is used to calculate the electric field due to multiple charges by calculating the electric field due to each charge and then summing the vectors to find the net electric field. This is based on the principle that the electric field at any point in space is the vector sum of the electric fields due to all the charges present in that space.
|
74 videos|314 docs|88 tests
|
FAQs on Electric Field & Electric Field Lines - Physics Class 12 - NEET
| 1. What is the formula for calculating the electric field due to a point charge? |  |
| 2. How do you determine the direction of the electric field produced by a point charge? |  |
| 3. How is the electric field due to a system of point charges calculated? |  |
| 4. What are electric field lines and what do they represent? |  |
| 5. What are the properties of electric field lines? |  |






















