Series L-R, C-R & C-R Circuit | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| Series L-R Circuit |

|
| Series C-R Circuit |

|
| L.C. Circuit |

|
| Series L-C-R Circuit |

|
Series L-R Circuit
- Now consider an ac circuit consisting of a resistor of resistance R and an inductor of inductance L in series with an ac source generator.
- Suppose in phasor diagram, current is taken along positive x-direction. The VR is also along positive x-direction and VL along positive y-direction as we know that potential difference across a resistance in ac is in phase with current and it leads in phase by 90º with current across the inductor, and as we know VR = i0R & V0 = i0XL
i = i0 sin wt
VR(t) = i0 Rsin ωt
VL(t) = i0 XL sin (ωt + p/2)
hence we can write
V(t) = i0R sin ωt + i0 XL sin (ωt + p/2)
V0 = i0
whereis known as impedence (z) of the circuit.
now we can write
where tan β=
hence β =
Example 1. When 100 volt dc is applied across a coil, a current of 1 amp flows through it; when 100 V ac of 50 Hz is applied to the same coil, only 0.5 amp flows. Calculate the resistance of inductance of the coil.
Sol. In case of a coil, i.e., L - R circuit.
i = with Z =
=
So when dc is applied, ω = 0, so z = R
and hence i = i.e., R =
=
= 200 ?
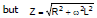 i.e., ω2L2 = Z2-R2
i.e., ω2L2 = Z2-R2
i.e., (2πfL)2 = 2002 - 1002 = 3 × 104 (as ω = 2πf)
So, L = =
= 0.55 H
Example 2. A 12 ohm resistance and an inductance of 0.05/p henry with negligible resistance are connected in series. Across the end of this circuit is connected a 130 volt alternating voltage of frequency 50 cycles/second. Calculate the alternating current in the circuit and potential difference across the resistance and that across the inductance.
Sol. The impedance of the circuit is given by
Z = =
= 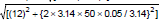 =
= = 13 ohm
Current in the circuit i = E/Z = = 10 amp
Potential difference across resistance
VR = iR = 10 × 12 = 120 volt
Inductive reactance of coil XL = ωL = 2πfL
Therefore, XL = 2π × 50 × = 5 ohm
Potential difference across inductance
VL = i × XL = 10 × 5 = 50 volt
Series C-R Circuit
Now consider an ac circuit consisting of a resistor of resistance R and an capacitor of capacitance C in series with an ac source generator.
Suppose in phasor diagram current is taken along positive x-direction. Then VR is also along positive x-direction but VC is along negative y-direction as potential difference across a capacitor in ac lags in phase by 90º with the current in the circuit. So we can write,
VR = I0 R sin ωt
Potential difference across capacitor
Potential at any instant t
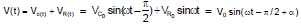
V(t) = V0 sin (ωt + b)
tan α =
Example 3. An A.C. source of angular frequency w is fed across a resistor R and a capacitor C in series. The current registered is i. If now the frequency of the source is changed to ω/3 (but maintaining the same voltage), the current in the circuit is found to be halved. Calculate the ratio of reactance to resistance at the original frequency.
Sol. At angular frequency w, the current in R-C circuit is given by
irms = ...(i)
When frequency is changed to ω/3, the current is halved. Thus
=
...(ii)
From equations (i) and (ii), we have
=
Solving this equation, we get
Hence, the ratio of reactance to resistance is
Example 4. A 50 W, 100 V lamp is to be connected to an ac mains of 200 V, 50 Hz. What capacitance is essential to be put in series with the lamp?
Sol. As resistance of the lamp R = = 200 ? and the maximum current i =
=
=
; so when the lamp is put in series with a capacitance and run at 200 V ac, from V =iZ we have,
Z = =
= 400?
Now as in case of C-R circuit, Z = ,
i.e., R2 + = 160000
or, = 16 × 104 - (200)2 = 12 × 104
So, =
× 102
or C =
i.e., C = = 9.2 μF
L.C. Circuit
As shown in figure a capacitor and inductance are connected in series method and alternating voltage is applied across the circuit.
Let Xc is capacitance reactance,
XL is Inductance reactance,
i = i0 sin wt current flowing through the circuit
VC(t) = i0 XC sin (ωt - π/2)
VL(t) = i0 XL sin (ωt + π/2)
= i0 XC sin wt cos π/2 - i0 XC cos wt sin π/2 + i0 XL sin wt cos π/2 + i0 XL cos wt sin π/2
= i0 cos w t(XL - XC)
V(t) = V0sin (wt + p/2)
V0 = i0Z 
Z = (XL - XC)
cos 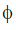 = 0
= 0
VCO = i0 XC ;
Series L-C-R Circuit
Now consider an ac circuit consisting of a resistor of resistance R, a capacitor of capacitance C and an inductor of inductance L are in series with an ac source generator.
Suppose in a phasor diagram current is taken along positive x-direction. Then VR is along positive x-direction, VL along positive y-direction and VC along negative y-direction, as potential difference across an inductor leads the current by 90° in phase while that across a capacitor, lags by 90°.
V =
L - R - C circuit
Impedance phasor of above circuit
& Impedance triangle
here B is phase angle By triangle tan β= 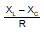
Power factor cos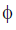 =
=
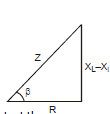
Let I be the current in the series circuit of any instant then
(1) Voltage V(t) = V0 sin (ωt + β) = i0 z sin (ωt + β)
here v0 = i0z & vrms = irmsz
(2) here voltage VL across the inductance is ahead of current I in phase by π/2 rad
(3) VC(t) = VO C sin (ωt - π/2)
here voltage VC across the capacitance lags behind the current I in phase by π/2 rad
(4) VR(t) = i0 R sin ωt
here voltage VR across the resistor R has same phase as I
VO R = IO R
Special Case :
(1) When XL > XC or VL > VC then emf is ahead of current by phase β which is given by
tan β = or cos f =
The series LCR circuit is said to be inductive
(2) When XL < XC or VL < VC then current is ahead of emf by phase angle β which is given by
or
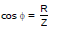
The series LCR circuit is said to be capacitive
(3) When XL = XC or VL = VC, b = 0, the emf and current will be in the same phase. The series LCR circuit is said to be purely resistive. It may also be noted that
or
or IRms =
Susceptance : The reciprocal of the reactane of an a.c. circuit is called its susceptance.
Admittance : The reciprocal of the impedance of an a.c. circuit is called its admittance.
Ex.10 Figure shows a series LCR circuit connected to a variable voltage source V = 10 sin (ωt + p/4) ;
xL = 10 ?, XC = 6 ?, R = 3 ?
Calculate Z, i0, irms, vrms, VL O, VC O, VR O, b,
VL Rms, VC Rms, VRms, i(t), VL(t), Vc(t), and VR(t)
XL > XC
Sol. V = 10 sin (wt + p/4) so V0 = 10 volt
Vrms =
Therefore, Z = 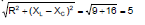
;
;
;
i(t) = 20 sin (ωt + π/4 - 53°)
VL(t) = 20 sin (ωt + π/4 - 53° + π/2)
= 20 sin (ωt + - 53° -
) = 12 sin (ωt -
- 53°)
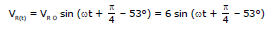
Ex.11 A resistor of resistance R, an inductor of inductance L and a capacitor of capacitance C all are connected in series with an a.c. supply. The resistance of R is 16 ohm and for a given frequency the inductive reactance of L is 24 ohm and capacitive reactance of C is 12 ohm. If the current in the circuit is 5 amp., find
(a) the potential difference across R, L and C (b) the impedance of the circuit
(c) the voltage of a.c. supply (d) phase angle
Sol. (a) Potential difference across resistance
VR = iR = 5 × 16 = 80 volt
Potential difference across inductance
VL = i × (wL) = 5 × 24 = 120 volt
|
268 videos|740 docs|171 tests
|
FAQs on Series L-R, C-R & C-R Circuit - Physics for JEE Main & Advanced
| 1. What is a Series L-R circuit? |  |
| 2. What is the significance of a Series C-R circuit? |  |
| 3. What is an L.C. circuit? |  |
| 4. What is the purpose of a Series L-C-R circuit? |  |
| 5. What are some applications of Series L-R, C-R, and L-C-R circuits? |  |





















