Algebra of Complex Numbers | Mathematics (Maths) for JEE Main & Advanced PDF Download
Complex Numbers
A. Definition
Complex numbers are defined as expressions of the form a + ib where a , b ∈ R &  It is denoted by z i.e. z = a + ib . ‘a’ is called as real part of z (Re z) and ‘b’ is called as imaginary part of z (Im z).
It is denoted by z i.e. z = a + ib . ‘a’ is called as real part of z (Re z) and ‘b’ is called as imaginary part of z (Im z).
Every Complex Number Can Be Regarded As
Purely real - Purely imaginary - Imaginary
if b = 0 - if a = 0 - if b ≠ 0
Remark :
(a) The set R of real numbers is a proper subset of the complex numbers . Hence the complete number system is 
(b) Zero is both purely real as well as purely imaginary but not imaginary .
(c)  is called the imaginary unit . Also i² = - l ; i3 = -i ; i4 = 1 etc.
is called the imaginary unit . Also i² = - l ; i3 = -i ; i4 = 1 etc.
(d)  only if atleast one of either a or b is non - negative.
only if atleast one of either a or b is non - negative.
B. Algebraic Operations
The algebraic operations on complex numbers are similar to those on real numbers treating ‘i’ as a polynomial . Inequalities in complex numbers are not defined . There is no validity if we say that complex number is positive or negative.
e.g. z > 0 , 4 + 2i < 2 + 4 i are meaningless.
However in real numbers if a2 + b2 = 0 then a = 0 = b but in complex numbers,
z12 + z22 = 0 does not imply z1 = z2 = 0.
Equality In Complex Number :
Two complex numbers 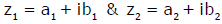 are equal if and only if their real & imaginary parts coincide.
are equal if and only if their real & imaginary parts coincide.
C.Conjugate Complex
If z = a + ib then its conjugate complex is obtained by changing the sign of its imaginary part & is denoted by 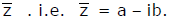
Remark :
(i) 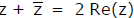
(ii) 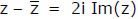
(iii) 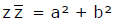 which is real
which is real
(iv)If z lies in the 1st quadrant then  lies in the 4th quadrant and -
lies in the 4th quadrant and - 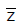 lies in the 2nd quadrant.
lies in the 2nd quadrant.
Ex.1 Express (1 + 2i)2/(2 + i)2 in the form x + iy.
Sol.
Ex.2 Show that a real value of x will satisfy the equation 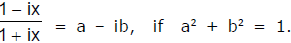
Sol.
We have
or [by componendo and dividendo],
Therefore, x will be real, if 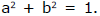
Ex.3 Find the square root of a + ib
Sol.
Let  = x + iy, where x and y are real. Squaring, a + ib =
= x + iy, where x and y are real. Squaring, a + ib = 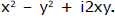
Equating real and imaginary parts, 
Now (x2 + y2)2 = (x2 – y2)2 + 4x2y2 = a2 + b2 or x2 + y2 = √(a2 + b2 )...(iii)
[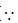 x and y are real, the sum of their squares must be positive]
x and y are real, the sum of their squares must be positive]
From (i) and (iii),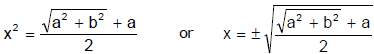

If b is positive, both x and y have the same signs and in opposite case, contrary signs. [by (ii)].
|
209 videos|447 docs|187 tests
|
FAQs on Algebra of Complex Numbers - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the algebraic representation of a complex number? |  |
| 2. How do you add complex numbers? |  |
| 3. How do you multiply complex numbers? |  |
| 4. How do you find the conjugate of a complex number? |  |
| 5. How do you represent complex numbers in polar form? |  |





















