Types of Vectors | Mathematics (Maths) for JEE Main & Advanced PDF Download
A vector has direction and magnitude both but scalar has only magnitude.

- Magnitude of a vector a is denoted by |a| or a. It is non-negative scalar.
- Direction of a vector is the angle made by the vector with the horizontal axis, that is, the X-axis. The direction of a vector formula is related to the slope of a line. We know that the slope of a line that passes through the origin and a point (x, y) is y/x. We also know that if θ is the angle made by this line, then its slope is tan θ, i.e., tan θ = y/x. Hence, θ = tan-1 (y/x).

Equality of Vectors
Two vectors a and b are said to be equal written as a = b, if they have (i) same length (ii) the same or parallel support and (iii) the same sense.
Types of Vectors
(i) Zero or Null Vector
A vector whose initial and terminal points are coincident is called zero or null vector. It is denoted by 0.
(ii) Unit Vector
A vector whose magnitude is unity is called a unit vector which is denoted by nˆ
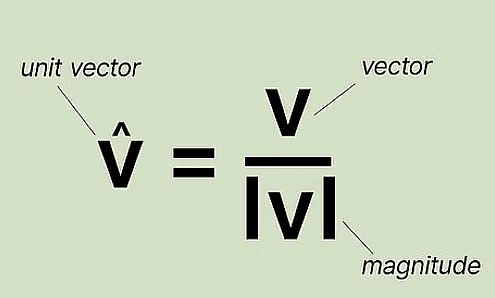
(iii) Negative of a Vector
A vector having the same magnitude as that of a given vector a and the direction opposite to that of a is called the negative of a and it is denoted by —a.
(iv) Like and Unlike Vectors
Vectors are said to be like when they have the same direction and unlike when they have opposite direction.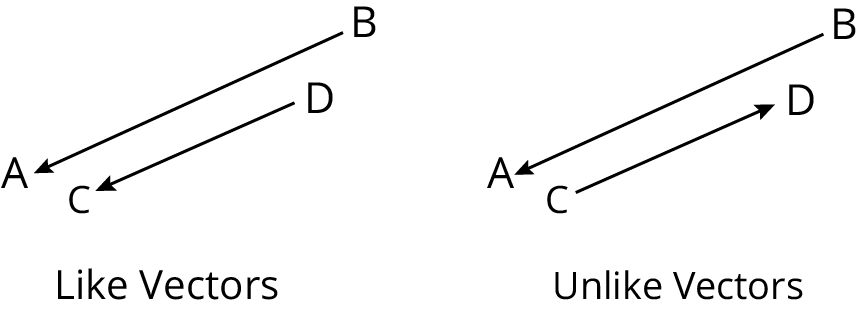
(v) Collinear or Parallel Vectors
Vectors having the same or parallel supports are called collinear vectors.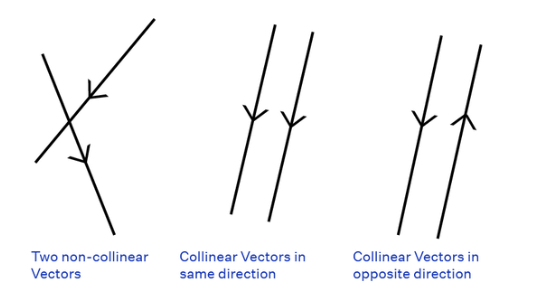
(vi) Coinitial Vectors
Vectors having same initial point are called coinitial vectors.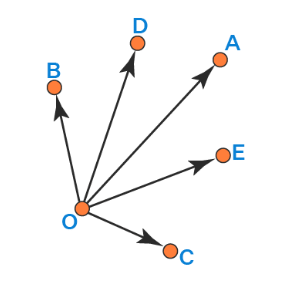
(vii) Localized Vectors
A vector which is drawn parallel to a given vector through a specified point in space is called localized vector.
(viii) Coplanar Vectors
A system of vectors is said to be coplanar, if their supports are parallel to the same plane. Otherwise they are called non-coplanar vectors.
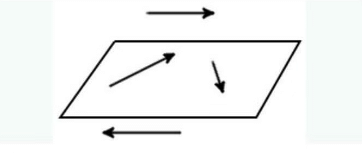
Example: In the figure given below, identify Collinear, Equal and Coinitial vectors:
Solution: By definition, we know that
- Collinear vectors are two or more vectors parallel to the same line irrespective of their magnitudes and direction. Hence, in the given figure, the following vectors are collinear:

- Equal vectors have the same magnitudes and direction regardless of their initial points. Hence, in the given figure, the following vectors are equal:
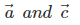
- Coinitial vectors are two or more vectors having the same initial point. Hence, in the given figure, the following vectors are coinitial:
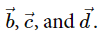
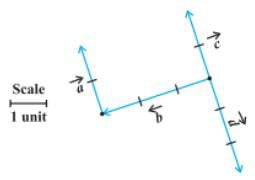
Example: In the given figure, identify the following vectors
- Coinitial
- Equal
- Collinear but not equal

Solution:
- Coinitial vectors have the same initial point. In the figure given above, vectors
 are the two vectors which have the same initial point P.
are the two vectors which have the same initial point P. - Equal vectors have same magnitudes and direction. In the figure given above, vectors
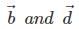 are equal vectors.
are equal vectors. - Collinear vectors are two or more vectors parallel to the same line. In the figure given above, vectors
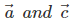 are parallel and hence, collinear. Also, vectors
are parallel and hence, collinear. Also, vectors 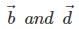 are parallel and hence, collinear. We know that vectors
are parallel and hence, collinear. We know that vectors 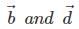 are also equal. Hence, vectors
are also equal. Hence, vectors 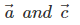 are collinear but not equal.
are collinear but not equal.
|
176 videos|582 docs|160 tests
|
FAQs on Types of Vectors - Mathematics (Maths) for JEE Main & Advanced
| 1. What are the different types of vectors based on direction? |  |
| 2. How are unit vectors defined in the context of vectors? |  |
| 3. Can you provide examples of parallel vectors in real-world scenarios? |  |
| 4. What is the significance of position vectors in vector analysis? |  |
| 5. How are zero vectors defined and what role do they play in vector algebra? |  |






















