Number System | GATE Notes & Videos for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Introduction |

|
| Types of Number Systems |

|
| Why Different Systems Matter |

|
| Advanced Concepts in Number Systems |

|
| Electronic Storage of Numbers |

|
| Alphanumeric Codes |

|
| ASCII |

|
| Unicode |

|
Introduction
Most people think of the decimal system (based on 10) as the go-to number system. It’s what we use every day—counting on our 10 fingers feels natural! But there are many other number systems out there, and they’re used for specific reasons. For example:
- Clocks and compasses use a system based on 60 (from the ancient Babylonians). Why? Because 60 can be divided evenly by 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, and 30—way more options than 10, which only splits evenly by 1, 2, and 5.
- Computers use the binary system (based on 2) because it matches their "on or off" electronic signals.

In digital systems, number systems help represent information using digits. The value of a digit depends on:
- The digit itself.
- Its position (or index).
- The base (total number of digits in the system). For example, in decimal (0–9), the base is 10.
Different number systems suit different purposes—some are ancient, others are modern, but all are still useful today. Let’s explore the main ones!
Types of Number Systems
In the digital computer, there are various types of number systems used for representing information.

1. Binary Number System (Base 2)
Generally, a binary number system is used in the digital computers. In this number system, it carries only two digits, either 0 or 1. There are two types of electronic pulses present in a binary number system.
The first one is the absence of an electronic pulse representing '0'and second one is the presence of electronic pulse representing '1'. Each digit is known as a bit. A four-bit collection (1101) is known as a nibble, and a collection of eight bits (11001010) is known as a byte.
The location of a digit in a binary number represents a specific power of the base (2) of the number system.
Key terms:
Bit: One digit (0 or 1).
Nibble: 4 bits (e.g., 1101).
Byte: 8 bits (e.g., 11001010).
How it works: Each position is a power of 2.
Example: (10100)₂ = (1 × 2⁴) + (0 × 2³) + (1 × 2²) + (0 × 2¹) + (0 × 2⁰)
= 16 + 0 + 4 + 0 + 0 = 20 in decimal.Examples: (10100)₂, (11011)₂, (11001)₂, (000101)₂, (011010)₂.
2. Decimal Number System (Base 10)
- The decimal numbers are used in our day to day life. The decimal number system contains ten digits from 0 to 9(base 10). Here, the successive place value or position, left to the decimal point holds units, tens, hundreds, thousands, and so on.
- The position in the decimal number system specifies the power of the base (10). The 0 is the minimum value of the digit, and 9 is the maximum value of the digit. For example, the decimal number 2541 consist of the digit 1 in the unit position, 4 in the tens position, 5 in the hundreds position, and 2 in the thousand positions and the value will be written as:
How it works: Each position represents a power of 10.
Example: 2541 = (2 × 1000) + (5 × 100) + (4 × 10) + (1 × 1)
= (2 × 10³) + (5 × 10²) + (4 × 10¹) + (1 × 10⁰)
= 2000 + 500 + 40 + 1 = 2541Examples: 123, 4567, 908.
3. Octal Number System (Base 8)
The octal number system has base 8(means it has only eight digits from 0 to 7). There are only eight possible digit values to represent a number. With the help of only three bits, an octal number is represented. Each set of bits has a distinct value between 0 and 7.
Below, we have described certain characteristics of the octal number system:
Characteristics:
- An octal number system carries eight digits starting from 0, 1, 2, 3, 4, 5, 6, and 7.
- It is also known as the base 8 number system.
- The position of a digit represents the 0 power of the base(8). Example: 80
- The position of the last digit represents the x power of the base(8). Example: 8x, where x represents the last position, i.e., 1

Examples:
(273)8, (5644)8, (0.5365)8, (1123)8, (1223)8.
4. Hexadecimal Number System (Base 16)
- It is another technique to represent the number in the digital system called the hexadecimal number system.The number system has a base of 16 means there are total 16 symbols(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F) used for representing a number.
- The single-bit representation of decimal values10, 11, 12, 13, 14, and 15 are represented by A, B, C, D, E, and F.
- Only 4 bits are required for representing a number in a hexadecimal number. Each set of bits has a distinct value between 0 and 15.
There are the following characteristics of the octal number system:
Characteristics:- It has ten digits from 0 to 9 and 6 letters from A to F.
- The letters from A to F defines numbers from 10 to 15.
- It is also known as the base 16number system.
- In hexadecimal number, the position of a digit represents the 0 power of the base (16). Example: 160
- In hexadecimal number, the position of the last digit represents the x power of the base(16). Example: 16x, where x represents the last position, i.e., 1
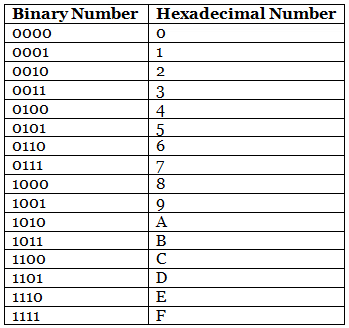 Examples:
Examples:
(FAC2)16, (564)16, (0ABD5)16, (1123)16, (11F3)16.
Why Different Systems Matter
- Ancient Roots: The Babylonian base-60 system lives on in time (60 seconds, 60 minutes) and angles (360 degrees).
- Human Use: Decimal (base 10) is natural for us, while farmers in northern Britain once used base-20 (a "score") to count animals—20, 40, 60, up to "four score" (80)—well into the 20th century!
- Tech Use: Binary (base 2) powers all digital devices because it’s simple for "on/off" circuits.
Advanced Concepts in Number Systems
Radix Point
The radix point scales a number’s value—like how 456.210 is 10 times bigger than 45.6210. In base 10, we call it the "decimal point," but for other systems like binary or hex, it’s just the "radix point." It’s the marker that separates whole numbers from fractions, adjusting the number’s size based on its position.Exponents
Each digit’s value comes from the radix raised to a power, depending on its spot relative to the radix point. For example, in hex, 98.216 is (9 × 16¹) + (8 × 16⁰) + (2 × 16⁻¹); in octal, 56.28 is (5 × 8¹) + (6 × 8⁰) + (2 × 8⁻¹); and in binary, 10.12 is (1 × 2¹) + (0 × 2⁰) + (1 × 2⁻¹). These exponents define how much each position contributes.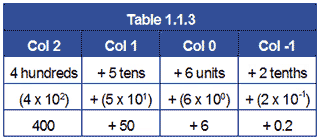
Floating Point Notation
Floating point notation shifts the radix point by tweaking the exponent, keeping the number’s value the same. Take 102.610: it can be written as 1.026 × 10², moving the point left and raising the exponent. This trick lets calculators and computers handle numbers flexibly, especially with fractions.
Electronic Storage of Numbers
Normalized Form
In electronic systems, numbers are stored in normalized form, with the radix point placed left of the most significant digit—like .110112 × 2³ for the binary number 110.112. Since binary digits are only 1s and 0s, the radix point can’t be stored within the number itself. Instead, the normalized value and its exponent are saved separately. When the number is displayed, the exponent restores the radix point to its correct position, ensuring accurate representation.Bits and Grouping
A single binary digit is called a bit (short for Binary DigIT). Using just one bit limits calculations, so bits are grouped: 4 bits = 1 nibble, 8 bits = 1 byte, and larger sets like 16 bits, 32 bits, or 64 bits are called words—e.g., a 32-bit word. The word length depends on how many bits the system can process or store at once, enabling more complex math as the group size grows.Storage in Registers
Numbers are stored in fixed-bit memory locations, some for general storage, others as specialized registers. For example, decimal 13, which is 11012 in 4-bit binary, becomes 000011012 in an 8-bit register by adding four non-significant zeros to the left of the most significant ‘1’. This padding ensures consistency. An n-bit register holds 2ⁿ values: an 8-bit register supports 2⁸ = 256 values (0–255), while a 4-bit register holds 2⁴ = 16 values (0–15), defining the range of storable numbers.Alphanumeric Codes
Purpose and Basics
Early computers were purely calculators, but today they handle text—names, addresses, descriptions—using alphanumeric codes. These binary codes represent letters, numbers, symbols, and punctuation as 1s and 0s, since computers are digital systems. They enable interfacing with devices like keyboards, monitors, and printers, expanding computers beyond numeric tasks.Morse Code
Invented in 1837 by Samuel F.B. Morse, Morse code was the first alphanumeric code for telecommunication. It uses short (dots) and long (dashes) elements—e.g., A = dot-dash, 5 = 5 dots, with a dash equaling three dots in International Morse. These can be sounds, marks, or pulses. Its variable character lengths (e.g., A vs. 5) prevented automation, but it’s still used in telegraph lines, radio circuits, and by pilots or air traffic controllers for identity and info transmission.
Baudot Code
The Baudot code, created in 1870 by French engineer Emile Baudot, was a popular 1860s alphanumeric code. It’s a 5-bit code (five elements per character), with all symbols of equal duration—unlike Morse—allowing telegraph transmission of the Roman alphabet, punctuation, and control signals. This uniformity made it more adaptable to early automated systems.
Hollerith Code
In 1896, Herman Hollerith’s Tabulating Machine Company developed punched-card machines, leading to IBM after mergers. The Hollerith code used 12-bit sequences on these cards—e.g., a string splits into two 6-bit ASCII chars: punches 12,0,2,4,6,8 and 11,1,3,5,7,9, interleaved to form the original 12 bits. Bit 7 is always 0, bit 6 complements bit 5 for ASCII compatibility. As punched cards faded, so did Hollerith, replaced by modern storage media.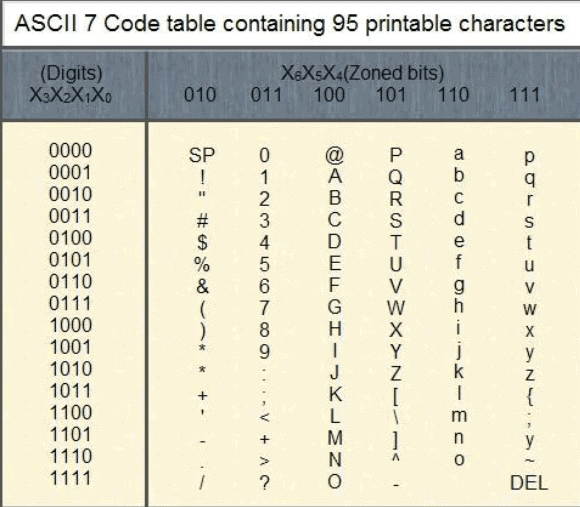
ASCII
The American Standard Code for Information Interchange (ASCII), pronounced "as-kee," emerged in 1967 (updated 1986) as a 7-bit code (128 characters) based on English alphabet order. It includes 95 printable characters—26 uppercase (A–Z), 26 lowercase (a–z), 10 numerals (0–9), 33 specials (e.g., + = 0101011)—plus 33 non-printing controls. Examples: A = 1000001, 9 = 0111001, d = 1100100. The 8-bit version (ASCII-8) adds a parity bit (e.g., A = 01000001), supporting 256 characters. Typing "PRINT X" on an ASCII-7 keyboard yields 1010000101001010010101001110101010001000001011000 (hex 50 52 49 4E 54 30 58). Another case: ASCII-8 message 10110001, 10110101, 10100101, 10100101, 10101110 translates to QUEEN (Q, U, E, E, N).
Extended Binary Coded Decimal Interchange Code (EBCDIC)
The Extended Binary Coded Decimal Interchange Code (EBCDIC) pronounced as "ebi-si disk" is another frequently used code by computers for transferring alphanumeric data. It is 8-bit code in which the numerals (0-9) are represented by the 8421 BCD code preceded by 1111. Since it is a 8-bit code, it can almost represent 23 (= 256) different characters which include both lowercase and uppercase letters in addition to various other symbols and commands.

EBCDIC was designed by IBM corp. so it is basically used by several IBM· models. In this code, we do not use a straight binary sequence for representing characters, as was in the case of ASCII code. Since it is a 8-bit code, so it can be easily grouped into groups of 4 so as to represent in arm of hexadecimal digits. By using the hexadecimal number system notation, the amount of digits used to represent various characters and special characters using EBCDIC code is reduced in volume of one is to four. Thus 8-bit binary code could be reduced to 2 hexadecimal digits which are easier to decode if we want to view the internal representation in memory. The above table lists the EBCDIC code for certain characters.
Read the above table as you read the graph. Suppose you want to search for EBCDIC code for letter 'A’. To that case, the value of X3 X2 Xl X0 bits is 0001 and value X7 X6 X5 X4 bits is 1100.
Therefore, EBCDIC code for letter 'A’ is 11000001(A). Similarly, the EBCDIC code for 'B' is 11000010(B).
The EBCDIC code '=' is 01111110
The EBCDIC code for '$' is 0101 1011
Unicode
The ASCII and EBCDIC encodings and their variants that we have studied suffer from some limitations.
1. These encodings do not have a sufficient number of characters to be able to encode alphanumeric data of all forms, scripts and languages. As a result, they do not permit multilingual computer processing.
2. These encoding suffer from incompatibility. For example: code 7A (in hex) represents the lowercase letter 'Z' in ASCII code and the semicolon sign ';' in EBCDIC code.
To overcome these limitations, UNICODE also known as universal code was developed jointly by the Unicode Consortium and the International Organization for Standardization (ISO). The Unicode is a 16-bit code so it can represent 65536 different characters. It is the most complete character encoding scheme that allows text of all forms and languages to be encoded for use by computers. In addition to multilingual support, it also supports a comprehensive set of mathematical and technical symbols, greatly simplifying any scientific information interchange.
UNICODE has a number of uses:
2. All World Wide Web consortium recommendations have used Unicode as their document character set since HTML 4.0.
3. It partially addresses the new line problem that occurs when trying to read a text file on different platforms. It defines a large number of characters that can be recognized as line terminators.
Unicode is currently being adopted by top computer industry leaders like Microsoft, Apple, Oracle, Sun, SAP and many more in their products.
|
27 videos|333 docs
|
FAQs on Number System - GATE Notes & Videos for Electrical Engineering - Electrical Engineering (EE)
| 1. What is the number system? |  |
| 2. How does the decimal number system work? |  |
| 3. What is the binary number system? |  |
| 4. How do you convert a decimal number to a binary number? |  |
| 5. What is the significance of the hexadecimal number system? |  |
















