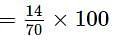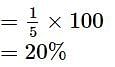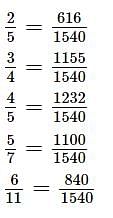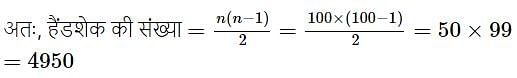Test: Number System (संख्या पद्धति) - 1 - UPSC MCQ
10 Questions MCQ Test - Test: Number System (संख्या पद्धति) - 1
निम्नलिखित प्रश्नों में प्रश्न चिह्न (?) के स्थान पर लगभग क्या मान आना चाहिए? (आप से सटीक मान की गणना करने के लिए आपेक्षित नहीं हैं।)
59.88 ÷ 12.21 × 635 = ?
59.88 ÷ 12.21 × 635 = ?
1 से 70 तक की संख्याओं में कितने प्रतिशत संख्याओं के वर्ग हैं जो कि अंक 1 में समाप्त होते हैं ?
एक पूर्ण वर्ग बनाने के लिए 599 में से कौन - सी सबसे छोटी संख्या को घटाया जाना चाहिए?
सबसे छोटी पूर्ण वर्ग संख्या, जो 2, 21, 36 और 56 से पूरी तरह से विभाज्य है, है:
वह सबसे छोटी संख्या कौन सी है जिसे 4,6,8 और 9 से विभाजित करने पर प्रत्येक स्थिति में शेषफल शून्य प्राप्त होता है और जब 13 से विभाजित किया जाता है, तब शेषफल 7 प्राप्त होता है:
यदि भिन्नों 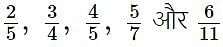 को उनके मानों के आरोही क्रम में व्यवस्थित किया जाता है, तो कौनसी भिन्न चौथी होगी?
को उनके मानों के आरोही क्रम में व्यवस्थित किया जाता है, तो कौनसी भिन्न चौथी होगी?
तीन क्रमागत संख्याओं का योग 87 है। इन तीन संख्याओं में से सबसे बड़ी संख्या ज्ञात कीजिए।
एक पार्टी में सौ मेहमान हैं यदि सभी एक दुसरे से सिर्फ एक बार हाथ मिलाते हैं, तो कितने हैंडशेक होते हैं?
एक घड़ी 1 बजे पर एक बार संघट्ट करती है, 2 बजे दो बार, 3 बजे तीन बार और इसी तरह से आगे। तो एक दिन में संघट्ट की कुल संख्या क्या है?
निम्नलिखित संख्या श्रृंखला में प्रश्न चिह्न (?) के स्थान पर क्या आना चाहिए?
963 × 874 = ?