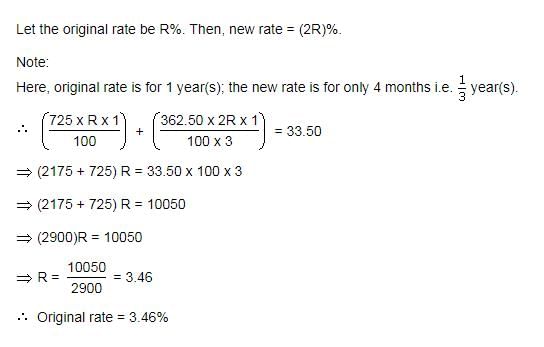Test: Simple Interest- 2 - Bank Exams MCQ
10 Questions MCQ Test - Test: Simple Interest- 2
A sum of Rs. 14,000 amounts to Rs. 22,400 in 12 years at the rate of simple interest. What is the rate of interest?
A sum of Rs. 725 is lent in the beginning of a year at a certain rate of interest. After 8 months, a sum of Rs. 362.50 more is lent but at the rate twice the former. At the end of the year, Rs. 33.50 is earned as interest from both the loans. What was the original rate of interest?
An automobile financier claims to be lending money at simple interest, but he includes the interest every six months for calculating the principal. If he is charging an interest of 10%, the effective rate of interest becomes:
A lent Rs. 5000 to B for 2 years and Rs. 3000 to C for 4 years on simple interest at the same rate of interest and received Rs. 2200 in all from both of them as interest. The rate of interest per annum is:
What annual payment will discharge a debt of Rs. 6450 due in 5 years at 10% per annum?
A lends Rs. 1500 to B and a certain sum to C at the same time at 8% per annum simple interest. If after 4 years, A altogether receives Rs. 1400 as interest from B and C, then the sum lent to C is A.
If the simple interest on a certain sum of money after 25/8 years is 1/4 of the principal, what is the rate of interest per annum?
A sum of Rs. 10 is lend to be returned in 11 monthly instalments of Rs. 1 each, interest being simple. The rate of interest charged is:
If a sum of Rs. 9 is lent to be paid back in 10 equal monthly installments of re. 1 each, then the rate of interest is
Divide Rs. 2379 into 3 parts so that their amount after 2,3 and 4 years respectively may be equal, the rate of interest being 5% per annum at simple interest. The first part is