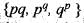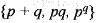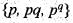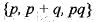|
|
Tapas BhowmikEduRev Mathematics |
|
|
Tapas Bhowmik
EduRev Mathematics
|
Content, tests & courses saved by you for accessing later. (visible to you only)
Top Scoring Tests by Tapas
Test: Order & Degree of Differential Equations | 40/40 |
Linear Algebra - 1 | 10/10 |
Test: Group Theory - 5 | 80/80 |
Differential Equations - 15 | 76/80 |
Differential Equations - 2 | 75/80 |
Vector Calculus - 2 | 75/80 |
Test: Group Theory - 3 | 75/80 |
Test: Linear Algebra - 3 | 75/80 |
Test: Linear Algebra - 7 | 75/80 |
Differential Equations - 6 | 75/80 |
Discussed Questions
|
|
Tapas Bhowmik asked • Dec 15, 2020 |
 be such that A has real eigenvalues then
be such that A has real eigenvalues then- a)θ = nπ for some integer n
- b)
 for some integer n
for some integer n - c)there is no restriction on θ
- d)
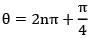 for some integer n
for some integer n
Correct answer is option 'A'. Can you explain this answer?
 be such that A has real eigenvalues then
be such that A has real eigenvalues thena)
θ = nπ for some integer n
b)
 for some integer n
for some integer nc)
there is no restriction on θ
d)
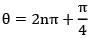 for some integer n
for some integer n

|
Sagar Shukla answered |
Eigen value are real in this case , that's why option c is right
|
|
Tapas Bhowmik asked • Dec 12, 2020 |
If G1 and G2 are commulator subgroup and centre of the dihedral group D4 respectively. Then select the incorrect statement.- a)G1 ∩ G2 ≠ {e}
- b)o(G1) | o(G2)
- c)o(G1) = 2
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If G1 and G2 are commulator subgroup and centre of the dihedral group D4 respectively. Then select the incorrect statement.
a)
G1 ∩ G2 ≠ {e}
b)
o(G1) | o(G2)
c)
o(G1) = 2
d)
None of these
|
|
Lavanya Patel answered |
The statement is incomplete and cannot be determined without further information. Please provide more information about the options or clarify the question.
|
|
Tapas Bhowmik asked • Dec 12, 2020 |
The set of complex number z with | z | = 1 under the operation * denote by z1 * z2 = | z1 | ·z2- a)group but not abelian
- b)group but not cyclic
- c)cyclic group
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
The set of complex number z with | z | = 1 under the operation * denote by z1 * z2 = | z1 | ·z2
a)
group but not abelian
b)
group but not cyclic
c)
cyclic group
d)
None of the above
|
|
Pranavi Kapoor answered |
The operation * on the set of complex numbers z with |z| = 1 is defined as follows:
For any two complex numbers z1 and z2 with |z1| = |z2| = 1, their operation * is given by:
z1 * z2 = |z1|
In other words, when two complex numbers z1 and z2 with magnitude 1 are multiplied under this operation *, the result is the magnitude of z1.
Note that the operation ... more
For any two complex numbers z1 and z2 with |z1| = |z2| = 1, their operation * is given by:
z1 * z2 = |z1|
In other words, when two complex numbers z1 and z2 with magnitude 1 are multiplied under this operation *, the result is the magnitude of z1.
Note that the operation ... more
|
|
Tapas Bhowmik asked • Dec 12, 2020 |
What is the maximum order of any element in A10- a)25
- b)24
- c)21
- d)20
Correct answer is option 'C'. Can you explain this answer?
What is the maximum order of any element in A10
a)
25
b)
24
c)
21
d)
20
|
|
Pranavi Kapoor answered |
To find the maximum order of any element in A10, we need to understand what A10 represents. In mathematics, A10 refers to the alternating group of degree 10, denoted as A10. The alternating group consists of even permutations, which are permutations that can be written as a product of an even number of transpositions.
In this case, A10 represents the set of all even permutations of 10 o... more
In this case, A10 represents the set of all even permutations of 10 o... more
|
|
Tapas Bhowmik asked • Dec 11, 2020 |
The number of conjugate classes of a non-abelian group of order 125 are- a)29
- b)25
- c)125
- d)1
Correct answer is option 'A'. Can you explain this answer?
The number of conjugate classes of a non-abelian group of order 125 are
a)
29
b)
25
c)
125
d)
1

|
Anurag Dhiman answered |
a group of order p^3 where p is prime have p^2 + p − 1 number of conjugacy class
|
|
Tapas Bhowmik asked • Dec 11, 2020 |
Which one is true?- a)Every quotient group of a group is abelian and its converse is also true.
- b)Every quotient group of a group is abelian but its converse is not true
- c)Every quotient group of an abelian group is abelian and its converse is also true.
- d)Every quotient group of an abelian group is abelian but the converse is not true.
Correct answer is option 'D'. Can you explain this answer?
Which one is true?
a)
Every quotient group of a group is abelian and its converse is also true.
b)
Every quotient group of a group is abelian but its converse is not true
c)
Every quotient group of an abelian group is abelian and its converse is also true.
d)
Every quotient group of an abelian group is abelian but the converse is not true.
|
|
Riya Chawla answered |
Explanation:
In order to understand the answer, we need to first define what a quotient group is and what it means for a group to be abelian.
Quotient Group:
Given a group G and a normal subgroup N of G, the quotient group G/N consists of the cosets of N in G with the group operation defined as (aN)(bN) = (ab)N, where aN and bN are cosets of N in G. In othe... more
In order to understand the answer, we need to first define what a quotient group is and what it means for a group to be abelian.
Quotient Group:
Given a group G and a normal subgroup N of G, the quotient group G/N consists of the cosets of N in G with the group operation defined as (aN)(bN) = (ab)N, where aN and bN are cosets of N in G. In othe... more
|
|
Tapas Bhowmik asked • Dec 11, 2020 |
If G is a group and H is a subgroup of index 2 in G then choose the correct statement.- a)H is a normal subgroup of G
- b)H is not a normal subgroup of G
- c)H is a subgroup of G
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If G is a group and H is a subgroup of index 2 in G then choose the correct statement.
a)
H is a normal subgroup of G
b)
H is not a normal subgroup of G
c)
H is a subgroup of G
d)
None of the above
|
|
Aakriti Yadav answered |
Explanation:
To understand why option A is the correct answer, we need to first understand the concept of a normal subgroup.
A subgroup H of a group G is said to be a normal subgroup if and only if for every element g in G, the conjugate of H by g is also a subset of H. In other words, for any h in H and g in G, the element ghg^(-1) is also in H.
Now, let's ... more
To understand why option A is the correct answer, we need to first understand the concept of a normal subgroup.
A subgroup H of a group G is said to be a normal subgroup if and only if for every element g in G, the conjugate of H by g is also a subset of H. In other words, for any h in H and g in G, the element ghg^(-1) is also in H.
Now, let's ... more
|
|
Tapas Bhowmik asked • Dec 11, 2020 |
Let F be a homomorphic mapping of a group G into a group G' Let (G) be the homomorphic image of G in G' then- a)F(G) is a complex of G'
- b)F(G) = G'
- c)F(G) is a subgroup of G'
- d)F(G) is a normal subgroup of G
Correct answer is option 'C'. Can you explain this answer?
Let F be a homomorphic mapping of a group G into a group G' Let (G) be the homomorphic image of G in G' then
a)
F(G) is a complex of G'
b)
F(G) = G'
c)
F(G) is a subgroup of G'
d)
F(G) is a normal subgroup of G

|
Essakiammal Ramya answered |
Recall the definition of a homomorphic image. [The homomorphic image of a group G under a homomorphism F:G → G' is the set of all elements in G' that are the image of some element in G.] F(G) = {[F(g) | g ∈ G]}.
Use the definition of a homomorphic image to determine which statement is correct.
[F(G) is a subset of G' by definition.]
[F(G) is a subgroup of G' because [it is closed under the operation in G', contains the identity element of G', and contains the inverse of each of its elements].]
[F(G) may not be equal to G' unless F is surjective.]
[F(G) is not necessarily a normal subgroup of G because [it is a subgroup of G', not G].]
Let G be a finite group of order 200, then the number of subgroup of G of order 25 is- a)1
- b)2
- c)5
- d)10
Correct answer is option 'A'. Can you explain this answer?
Let G be a finite group of order 200, then the number of subgroup of G of order 25 is
a)
1
b)
2
c)
5
d)
10
|
|
Tapas Bhowmik answered • Dec 11, 2020 |
Apply sylow theorem
|
|
Tapas Bhowmik upvoted • Dec 11, 2020 |
Let G be a finite group of order 200, then the number of subgroup of G of order 25 is- a)1
- b)2
- c)5
- d)10
Correct answer is option 'A'. Can you explain this answer?
Let G be a finite group of order 200, then the number of subgroup of G of order 25 is
a)
1
b)
2
c)
5
d)
10

|
Karan Kumar answered |
Correct answer is option 'A'
If general solution of the differential equation ay'" + by" + cy’ + dy = 0 is linearly spanned by ex, sinx and cosx, then which one of the following holds?- a)a + b - c - d = 0
- b)a + b + c + d = 0
- c)a - b + c - d = 0
- d)a - b - c - d=0
Correct answer is option 'B'. Can you explain this answer?
If general solution of the differential equation ay'" + by" + cy’ + dy = 0 is linearly spanned by ex, sinx and cosx, then which one of the following holds?
a)
a + b - c - d = 0
b)
a + b + c + d = 0
c)
a - b + c - d = 0
d)
a - b - c - d=0
|
|
Tapas Bhowmik answered • Dec 10, 2020 |
A=1 b=0 c=0 d=-1
Statement A : Every isomorphic image of a cyclic group is cyclic.
Statement B : Every homomorphic image of a cyclic group is cyclic
- a)B is true only
- b)Both A and B are false
- c)A is true only
- d)Both A and B are true
Correct answer is option 'D'. Can you explain this answer?
Statement A : Every isomorphic image of a cyclic group is cyclic.
Statement B : Every homomorphic image of a cyclic group is cyclic
Statement B : Every homomorphic image of a cyclic group is cyclic
a)
B is true only
b)
Both A and B are false
c)
A is true only
d)
Both A and B are true
|
|
Tapas Bhowmik answered • Dec 09, 2020 |
A is obviously true . if H be homomorphic image of G this means there is an isomorphism from G to H . so H also cyclic
Let < an> —> a. Let for every positive integer k, Ak be the set of all positive integer n such that | an- a | < —1/k. Then,- a)Ak is finite for all k
- b)Ak is finite for some k
- c)every Ak contains all but finitely many positive integers
- d)Ak contains all positive integers
Correct answer is option 'D'. Can you explain this answer?
Let < an> —> a. Let for every positive integer k, Ak be the set of all positive integer n such that | an- a | < —1/k. Then,
a)
Ak is finite for all k
b)
Ak is finite for some k
c)
every Ak contains all but finitely many positive integers
d)
Ak contains all positive integers
|
|
Tapas Bhowmik answered • Dec 09, 2020 |
I think C is correct
Let y be continuously differentiable function which satisfies the differential equation
y" + y' - y = 0, 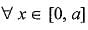
where a is a positive real number, if y(0) = y(a) - 0, then on [0, a].- a)y is strictly increasing
- b)y is strictly decreasing
- c)y is monotonic
- d)y has finite countably infinite number is zero
Correct answer is option 'C'. Can you explain this answer?
Let y be continuously differentiable function which satisfies the differential equation
y" + y' - y = 0,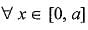
where a is a positive real number, if y(0) = y(a) - 0, then on [0, a].
y" + y' - y = 0,
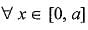
where a is a positive real number, if y(0) = y(a) - 0, then on [0, a].
a)
y is strictly increasing
b)
y is strictly decreasing
c)
y is monotonic
d)
y has finite countably infinite number is zero
|
|
Tapas Bhowmik answered • Dec 09, 2020 |
Y=0 we will get ie monotone but not strictly
|
|
Tapas Bhowmik upvoted • Dec 06, 2020 |
If 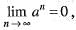 then
then
a)| a | ≥ 1 b)| a | ≤ 1c)| a | > 1d)| a | < 1Correct answer is option 'D'. Can you explain this answer?

|
Santosh Kumar Mandal answered |
Answer should be a
Fetching relevant content for you














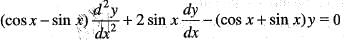 Given that y = sin x is a solution, is
Given that y = sin x is a solution, is

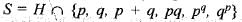 has exactly three elements. Then S is
has exactly three elements. Then S is