All Exams >
JEE >
6 Months Preparation for JEE >
All Questions
All questions of Continuity and Differentiability for JEE Exam
If xy = 2, then dy/dx is- a)-x2/2
- b)y2
- c)-2/x2
- d)-y/x
Correct answer is option 'D'. Can you explain this answer?
If xy = 2, then dy/dx is
a)
-x2/2
b)
y2
c)
-2/x2
d)
-y/x
|
|
Hansa Sharma answered |
xy = 2
x dy/dx + y = 0
x dy/dx = -y
dy/dx = -y/x
x dy/dx + y = 0
x dy/dx = -y
dy/dx = -y/x
Whta is the derivatve of y = log5 (x)- a)
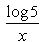
- b)
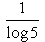
- c)

- d)
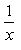
Correct answer is option 'C'. Can you explain this answer?
Whta is the derivatve of y = log5 (x)
a)
b)
c)
d)
|
|
Tanuja Kapoor answered |
y = log5 x = ln x/ln 5 → change of base
= ln x/ln 5
dy/dx = 1/ln5⋅1/x → 1/ln5 is a constant, so we don't change it
= 1/(x ln 5)
= ln x/ln 5
dy/dx = 1/ln5⋅1/x → 1/ln5 is a constant, so we don't change it
= 1/(x ln 5)
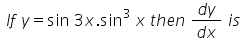
- a)3 cos2 x. cos 4x
- b)cos 3x. cos3x
- c)-9 cos 3x. cos2x sinx
- d)3 sin2x.sin 4x
Correct answer is option 'D'. Can you explain this answer?
a)
3 cos2 x. cos 4x
b)
cos 3x. cos3x
c)
-9 cos 3x. cos2x sinx
d)
3 sin2x.sin 4x
|
|
Deepak Kapoor answered |
Given: y = sin 3x . sin3

= 3 sin2x.sin 4x

= 3 sin2x.sin 4x
A real function f is said to be continuous if it is continuous at every point in …… .- a)[-∞,∞]
- b)The range of f
- c)The domain of f
- d)Any interval of real numbers
Correct answer is option 'A'. Can you explain this answer?
A real function f is said to be continuous if it is continuous at every point in …… .
a)
[-∞,∞]
b)
The range of f
c)
The domain of f
d)
Any interval of real numbers
|
|
Saranya Choudhury answered |
Its domain. This means that for any point x in the domain of f, as x approaches a certain value a, the value of f(x) approaches f(a). In other words, there are no sudden jumps or gaps in the graph of f.
More formally, a function f is continuous at a point a if:
1. f(a) is defined (i.e. a is in the domain of f).
2. The limit of f(x) as x approaches a exists (i.e. the left and right-hand limits are equal).
3. The limit of f(x) as x approaches a is equal to f(a).
If a function is continuous at every point in its domain, it is called a continuous function. Continuous functions have many useful properties and are often used in mathematical models and real-world applications.
More formally, a function f is continuous at a point a if:
1. f(a) is defined (i.e. a is in the domain of f).
2. The limit of f(x) as x approaches a exists (i.e. the left and right-hand limits are equal).
3. The limit of f(x) as x approaches a is equal to f(a).
If a function is continuous at every point in its domain, it is called a continuous function. Continuous functions have many useful properties and are often used in mathematical models and real-world applications.
If 3 sin(xy) + 4 cos (xy) = 5, then 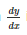 = .....
= .....- a)

- b)
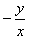
- c)
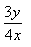
- d)

Correct answer is option 'B'. Can you explain this answer?
If 3 sin(xy) + 4 cos (xy) = 5, then 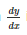 = .....
= .....
a)
b)
c)
d)

|
Dr Manju Sen answered |
3sinxy + 4cosxy = 5
⇒ 5(3/5 sinxy + 4/5 cosxy) = 5
⇒ (3/5 sinxy + 4/5 cosxy) = 1
now (3/5)²+(4/5)² = 1
so let, 3/5 = cosA
⇒ 4/5 = sinA
So , (3/5 sinxy + 4/5 cosxy) = 1
⇒ (cosAsinxy + sinAcosxy) = 1
⇒ sin(A+xy) = 1
⇒ A + xy = 2πk + π/2 (k is any integer)
⇒ sin⁻¹(4/5) + xy = 2πk + π/2
differenciating both sides with respect to x
0 + xdy/dx + y = 0
dy/dx = -y/x
⇒ 5(3/5 sinxy + 4/5 cosxy) = 5
⇒ (3/5 sinxy + 4/5 cosxy) = 1
now (3/5)²+(4/5)² = 1
so let, 3/5 = cosA
⇒ 4/5 = sinA
So , (3/5 sinxy + 4/5 cosxy) = 1
⇒ (cosAsinxy + sinAcosxy) = 1
⇒ sin(A+xy) = 1
⇒ A + xy = 2πk + π/2 (k is any integer)
⇒ sin⁻¹(4/5) + xy = 2πk + π/2
differenciating both sides with respect to x
0 + xdy/dx + y = 0
dy/dx = -y/x
Can you explain the answer of this question below:The derivatve of f(x) = 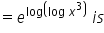
- A:
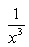
- B:
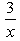
- C:
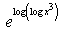
- D:
3x2
The answer is b.
The derivatve of f(x) =
3x2

|
.mie. answered |
Here in this function ....firstly... exponential and logarithmic fn are anti to each other...
and therefore cncl out ech other....
here..
in this e and log cncl out ech other... and we are left with ....
log x^3.....
acc to formula..
log m^n = n log m
therefore...
3 log x
so we reduced our eq to this
then taking derivative....
its 3/x
y = log(sec + tan x)
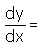
- a)sec x tan x – 1
- b)sec x
- c)sec x tan x + 1
- d)tan x
Correct answer is option 'B'. Can you explain this answer?
y = log(sec + tan x)
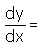
a)
sec x tan x – 1
b)
sec x
c)
sec x tan x + 1
d)
tan x
|
|
Lavanya Menon answered |
y = log(secx + tanx)
dy/dx = 1/(secx + tanx){(secxtanx) + sec2x}
= secx(secx + tanx)/(secx + tanx)
= secx
dy/dx = 1/(secx + tanx){(secxtanx) + sec2x}
= secx(secx + tanx)/(secx + tanx)
= secx
Which of the following functions are not continuous.- a)
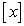
- b)
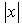
- c)ex
- d)
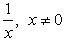
Correct answer is option 'A'. Can you explain this answer?
Which of the following functions are not continuous.
a)
b)
c)
ex
d)

|
Anu answered |
b,c,and d are continuous and [x] is discontinuous at integer points.
Derivatve of f(x) 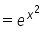 is given by
is given by
- a)
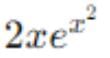
- b)
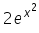
- c)
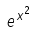
- d)

Correct answer is option 'A'. Can you explain this answer?
Derivatve of f(x) 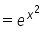 is given by
is given by
a)
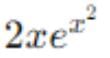
b)
c)
d)
|
|
Neha Sharma answered |
y 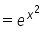
The derivative of y = ef(x)is dy/dx = f'(x)ef(x)
In this case, f(x) = x2 , and the derivative of x2 = 2x
Therefore, f'(x)= 2x,
dy/dx = 2x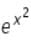
The derivative of y = ef(x)is dy/dx = f'(x)ef(x)
In this case, f(x) = x2 , and the derivative of x2 = 2x
Therefore, f'(x)= 2x,
dy/dx = 2x
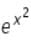
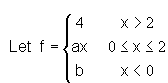 For what values of a and b, f is a continuous function.
For what values of a and b, f is a continuous function.- a)a=2,b=0
- b)a=1,b=0
- c)a=0,b=2
- d)a=0,b=0
Correct answer is 'A'. Can you explain this answer?
a)
a=2,b=0
b)
a=1,b=0
c)
a=0,b=2
d)
a=0,b=0
|
|
Tejas Verma answered |
For continuity: LHL=RHL
at x=2,
LHL: x < 2 ⇒ f(x) = 2*a
RHL: x ≥ 2 ⇒ f(x) = 4
For continuity: LHL = RHL
⇒ 2a = 4 ⇒ a = 2
LHL: x < 2 ⇒ f(x) = 2*a
RHL: x ≥ 2 ⇒ f(x) = 4
For continuity: LHL = RHL
⇒ 2a = 4 ⇒ a = 2
at x = 0,
LHL: x < 0 ⇒ f(x) = b
RHL: x ≥ 0 ⇒ f(x) = 0 * a
For continuity: LHL = RHL
⇒ b = 0
LHL: x < 0 ⇒ f(x) = b
RHL: x ≥ 0 ⇒ f(x) = 0 * a
For continuity: LHL = RHL
⇒ b = 0
Find the derivate of y = sin4x + cos4x- a)– sin 2x
- b)4 sin3 x + 4 cos3 x
- c)– sin 4x
- d)4 sin x cos x cos 2x
Correct answer is option 'C'. Can you explain this answer?
Find the derivate of y = sin4x + cos4x
a)
– sin 2x
b)
4 sin3 x + 4 cos3 x
c)
– sin 4x
d)
4 sin x cos x cos 2x

|
Mohit Rajpoot answered |
y=sin4x, and z=cos4x
So by using chain rule
df(x)/dx = dsin4x/dx + dcos4x/dx
=dy4/dy * dy/dx + dz4/dz * dzdx
=dy4/dy * dsinxdx + dz4/dz * dcosx/dx
=4y(4−1)⋅cosx+4z(4−1)⋅(−sinx)
=4sin3xcosx − 4cos3xsinx
=4sinxcosx(sin2x − cos2x)
=2sin2x(−cos2x)
=−2sin2xcos2x
=−sin4x
So by using chain rule
df(x)/dx = dsin4x/dx + dcos4x/dx
=dy4/dy * dy/dx + dz4/dz * dzdx
=dy4/dy * dsinxdx + dz4/dz * dcosx/dx
=4y(4−1)⋅cosx+4z(4−1)⋅(−sinx)
=4sin3xcosx − 4cos3xsinx
=4sinxcosx(sin2x − cos2x)
=2sin2x(−cos2x)
=−2sin2xcos2x
=−sin4x
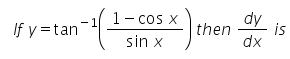
Correct answer is option 'A'. Can you exp... morelain this answer?
|
|
Aryan Khanna answered |
y = tan-1(1-cosx)/sinx
y = tan-1{2sin2(x/2)/(2sin(x/2)cos(x/2)}
y = tan-1{tan x/2}
y = x/2 => dy/dx = 1/2
y = tan-1{2sin2(x/2)/(2sin(x/2)cos(x/2)}
y = tan-1{tan x/2}
y = x/2 => dy/dx = 1/2
F(x) = tan (log x)
F'(x) =- a)sec2 (logx)
- b)
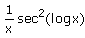
- c)
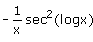
- d)-x sec2 (logx)
Correct answer is option 'B'. Can you explain this answer?
F(x) = tan (log x)
F'(x) =
F'(x) =
a)
sec2 (logx)
b)
c)
d)
-x sec2 (logx)

|
Virendra Singh answered |
I have chosen (b) but it is showing (d) is correct
Function f(x) = log x + 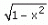 is continuous at
is continuous at- a)(0,1)
- b)[-1,1]
- c)(0,∞)
- d)(0,1]
Correct answer is option 'D'. Can you explain this answer?
Function f(x) = log x + 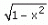 is continuous at
is continuous at
a)
(0,1)
b)
[-1,1]
c)
(0,∞)
d)
(0,1]
|
|
Om Desai answered |
- [-1,1] cannot be continuous interval because log is not defined at 0.
- The value of x cannot be greater than 1 because then the function will become complex.
- (0,1) will not be considered because its continuous at 1 as well. Hence D is the correct option.

- a)

- b)

- c)
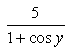
- d)
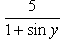
Correct answer is option 'C'. Can you explain this answer?
a)
b)
c)
d)
|
|
Poonam Reddy answered |
y + sin y = 5x
dy/dx + cos ydy/dx = 5
dy/dx = 5/(1+cos y)
dy/dx + cos ydy/dx = 5
dy/dx = 5/(1+cos y)
If f(x) = ex, then the value of f'(-3) is- a)log (3)
- b)e2
- c)log (-3)
- d)e-3
Correct answer is option 'D'. Can you explain this answer?
If f(x) = ex, then the value of f'(-3) is
a)
log (3)
b)
e
2
c)
log (-3)
d)
e-3

|
Infinity Academy answered |
As, f (x) = ex
Similarly, f (-3) = e-3
Similarly, f (-3) = e-3
Can you explain the answer of this question below:
- A:
1/2
- B:
0
- C:
1
- D:
none of these
The answer is b.
1/2
0
1
none of these

|
Shivani answered |
Apply L-hospital rule.....u will get the ans....

- a)

- b)

- c)

- d)

Correct answer is option 'B'. Can you explain this answer?
a)
b)
c)
d)

|
Suhani Dangarh answered |
Put x=tan thita. then you will get. 2 tan inverse x then differentiate

- a)

- b)
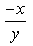
- c)
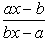
- d)
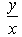
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
|
|
Rocky Gupta answered |
X^a y^b = (x + y)^(a + b)
taking ln on both sides :-
alnx + b lny = (a + b) ln(x + y)
diff both sides w.r.t x :-
a/x + by'/y = ( (a + b)/(x + y) ) + (((a + b) y'))/(x + y)
or,
a/x - (a +b)/(x + y) = y'[((a + b) / (x + y)) - b/y]
or,
(ax + ay - ax - bx)/x = y' [ (ay + by - bx - by)/y] (cancel (x + y))
or,
y' = dy/dx = ( y (ay - bx) )/(x( ay - bx)) = y/x
therefore we can easily say that the option (D) is the correct answer
taking ln on both sides :-
alnx + b lny = (a + b) ln(x + y)
diff both sides w.r.t x :-
a/x + by'/y = ( (a + b)/(x + y) ) + (((a + b) y'))/(x + y)
or,
a/x - (a +b)/(x + y) = y'[((a + b) / (x + y)) - b/y]
or,
(ax + ay - ax - bx)/x = y' [ (ay + by - bx - by)/y] (cancel (x + y))
or,
y' = dy/dx = ( y (ay - bx) )/(x( ay - bx)) = y/x
therefore we can easily say that the option (D) is the correct answer

- a)2t
- b)1/2a
- c)-t/2a
- d)t/4a
Correct answer is option 'B'. Can you explain this answer?
a)
2t
b)
1/2a
c)
-t/2a
d)
t/4a

|
Knowledge Hub answered |
y = at4, x = 2at2
dy/dt = 4at3 dx/dt = 4at => dt/dx = 1/4at
Divide dy/dt by dx/dt, we get
dy/dx = t2
d2 y/dx2 = 2t dt/dx……………….(1)
Put the value of dt/dx in eq(1)
d2 y /dx2 = 2t(1/4at)
= 1/2a
dy/dt = 4at3 dx/dt = 4at => dt/dx = 1/4at
Divide dy/dt by dx/dt, we get
dy/dx = t2
d2 y/dx2 = 2t dt/dx……………….(1)
Put the value of dt/dx in eq(1)
d2 y /dx2 = 2t(1/4at)
= 1/2a
Differentiate 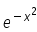 with respect to x.
with respect to x.- a)
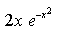
- b)
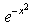
- c)
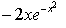
- d)
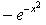
Correct answer is option 'C'. Can you explain this answer?
Differentiate 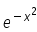 with respect to x.
with respect to x.
a)
b)
c)
d)
|
|
Tejas Verma answered |
y = e^(-x)2.................(1)
Put u = (-x)2
du/dx = -2x dx
Differentiating eq(1) y = eu
dy/du = e^u
⇒ dy/dx = (dy/du) * (du/dx)
= (eu) * (-2x)
⇒ - 2xe(-x2)
Put u = (-x)2
du/dx = -2x dx
Differentiating eq(1) y = eu
dy/du = e^u
⇒ dy/dx = (dy/du) * (du/dx)
= (eu) * (-2x)
⇒ - 2xe(-x2)
Examine the continuity of function 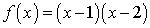
- a)Discontinuous at x=1,2
- b)Discontinuous at x=1
- c)Continuous everywhere.
- d)Discontinuous at x=2
Correct answer is option 'C'. Can you explain this answer?
Examine the continuity of function 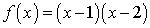
a)
Discontinuous at x=1,2
b)
Discontinuous at x=1
c)
Continuous everywhere.
d)
Discontinuous at x=2
|
|
Om Desai answered |
Lim f (x) = lim (x-1)(x-2) at x tend to k
► So it get k2-3k+2
► Now f (k) = k2 -3k+2
► So f (x) =f (k) so continous at everywhere
f (x) = max {x, x3},then the number of points where f (x) is not differentiable, are- a)1
- b) 2
- c)3
- d)4
Correct answer is option 'C'. Can you explain this answer?
f (x) = max {x, x3},then the number of points where f (x) is not differentiable, are
a)
1
b)
2
c)
3
d)
4
|
|
Gaurav Rane answered |
Solution:
To find the points where the given function is not differentiable, we need to find the points where the function is not continuous or where the derivative does not exist.
Step 1: Finding the points of non-differentiability where the function is not continuous.
Since the function is the maximum of two functions, we need to consider the points where these two functions are equal.
Let x = x³, then x³ - x = 0, which gives x = 0, 1.
Therefore, the function is not continuous at x = 0 and x = 1.
Step 2: Finding the points of non-differentiability where the derivative does not exist.
At x = 0, the left-hand derivative is 1 and the right-hand derivative is 0.
At x = 1, the left-hand derivative is 3 and the right-hand derivative is 0.
Therefore, the function is not differentiable at x = 0 and x = 1.
Hence, the function f(x) = max{x, x³} is not differentiable at three points, namely x = 0, x = 1, and wherever the function changes from x to x³ or vice versa.
Therefore, the correct option is (C) 3.
To find the points where the given function is not differentiable, we need to find the points where the function is not continuous or where the derivative does not exist.
Step 1: Finding the points of non-differentiability where the function is not continuous.
Since the function is the maximum of two functions, we need to consider the points where these two functions are equal.
Let x = x³, then x³ - x = 0, which gives x = 0, 1.
Therefore, the function is not continuous at x = 0 and x = 1.
Step 2: Finding the points of non-differentiability where the derivative does not exist.
At x = 0, the left-hand derivative is 1 and the right-hand derivative is 0.
At x = 1, the left-hand derivative is 3 and the right-hand derivative is 0.
Therefore, the function is not differentiable at x = 0 and x = 1.
Hence, the function f(x) = max{x, x³} is not differentiable at three points, namely x = 0, x = 1, and wherever the function changes from x to x³ or vice versa.
Therefore, the correct option is (C) 3.
If f(x) = x + cot x, 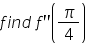
- a)-4
- b)2
- c)4
- d)-2
Correct answer is option 'C'. Can you explain this answer?
If f(x) = x + cot x, 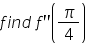
a)
-4
b)
2
c)
4
d)
-2
|
|
Aryan Khanna answered |
f(x) = x + cot x
f’(x) = 1 + (-cosec2 x)
f”(x) = 0 - 2cosec x(-cosec x cot x)
= 2 cosec2 x cot x
f”(π/4) = 2 cosec2 (π/4) cot(π/4)
= 2 [(2)^½]2 (1)
= 4
f’(x) = 1 + (-cosec2 x)
f”(x) = 0 - 2cosec x(-cosec x cot x)
= 2 cosec2 x cot x
f”(π/4) = 2 cosec2 (π/4) cot(π/4)
= 2 [(2)^½]2 (1)
= 4
What is the point of discontinuity for signum function?- a)x=1
- b)x=-1
- c)x=0
- d)function is continuous on R
Correct answer is option 'C'. Can you explain this answer?
What is the point of discontinuity for signum function?
a)
x=1
b)
x=-1
c)
x=0
d)
function is continuous on R
|
|
Arun Khanna answered |
It has a jumped discontinuity which means if the function is assigned some value at the point of discontinuity it cannot be made continuous. But the function is definitely discontinuous at x=0. the sgn function is a discontinuous function (isolated/jump discontinuity).
Find the second derivative of excosx- a)-2exsinx
- b)-exsinx
- c)ex(sinx + cosx)
- d)-2excosx
Correct answer is option 'A'. Can you explain this answer?
Find the second derivative of excosx
a)
-2exsinx
b)
-exsinx
c)
ex(sinx + cosx)
d)
-2excosx
|
|
Rounak Nair answered |
**Solution:**
To find the second derivative of the given function, we need to differentiate it twice with respect to x.
First, let's find the first derivative of the function:
f(x) = ex * cosx
Using the product rule, the derivative of f(x) is:
f'(x) = (ex * (-sinx)) + (cosx * ex)
= -ex * sinx + ex * cosx
= ex * (cosx - sinx)
Now, let's find the second derivative of the function. Taking the derivative of f'(x):
f''(x) = (ex * (-sinx)) + (ex * (-cosx))
= -ex * sinx - ex * cosx
= -ex * (sinx + cosx)
Therefore, the second derivative of excosx is -2exsinx, which is option A.
To find the second derivative of the given function, we need to differentiate it twice with respect to x.
First, let's find the first derivative of the function:
f(x) = ex * cosx
Using the product rule, the derivative of f(x) is:
f'(x) = (ex * (-sinx)) + (cosx * ex)
= -ex * sinx + ex * cosx
= ex * (cosx - sinx)
Now, let's find the second derivative of the function. Taking the derivative of f'(x):
f''(x) = (ex * (-sinx)) + (ex * (-cosx))
= -ex * sinx - ex * cosx
= -ex * (sinx + cosx)
Therefore, the second derivative of excosx is -2exsinx, which is option A.
The dervative of sin(x2) is- a)2x sin (x2)
- b)cos (x2)
- c)2x cos x2
- d)-2x cos x2
Correct answer is option 'C'. Can you explain this answer?
The dervative of sin(x2) is
a)
2x sin (x2)
b)
cos (x2)
c)
2x cos x2
d)
-2x cos x2
|
|
Sharmila Mishra answered |
Understanding the Derivative of sin(x²)
To find the derivative of the function sin(x²), we need to apply the chain rule of differentiation.
1. Chain Rule Explained
- The chain rule states that if you have a composite function, say f(g(x)), then the derivative is given by f'(g(x)) * g'(x).
- In our case, we can consider f(u) = sin(u) where u = x².
2. Applying the Chain Rule
- First, we need to differentiate the outer function sin(u):
- The derivative of sin(u) is cos(u).
- Next, differentiate the inner function u = x²:
- The derivative of x² is 2x.
3. Putting It All Together
- Using the chain rule:
- The derivative of sin(x²) = cos(x²) * 2x.
- Therefore, we write it as:
- 2x * cos(x²).
4. Final Result
- The derivative of sin(x²) is 2x cos(x²), which corresponds to option 'C'.
Summary
- The correct answer is option 'C': 2x cos(x²).
- This result highlights the importance of using the chain rule for composite functions in calculus, especially in problems like these commonly found in JEE exams.
To find the derivative of the function sin(x²), we need to apply the chain rule of differentiation.
1. Chain Rule Explained
- The chain rule states that if you have a composite function, say f(g(x)), then the derivative is given by f'(g(x)) * g'(x).
- In our case, we can consider f(u) = sin(u) where u = x².
2. Applying the Chain Rule
- First, we need to differentiate the outer function sin(u):
- The derivative of sin(u) is cos(u).
- Next, differentiate the inner function u = x²:
- The derivative of x² is 2x.
3. Putting It All Together
- Using the chain rule:
- The derivative of sin(x²) = cos(x²) * 2x.
- Therefore, we write it as:
- 2x * cos(x²).
4. Final Result
- The derivative of sin(x²) is 2x cos(x²), which corresponds to option 'C'.
Summary
- The correct answer is option 'C': 2x cos(x²).
- This result highlights the importance of using the chain rule for composite functions in calculus, especially in problems like these commonly found in JEE exams.
Let f(x) = x – [x], then f ‘ (x) = 1 for- a)all x ∈ I
- b)all x ∈ (R−I)
- c)all x ∈ R
- d)all x ∈ Rx- {0]
Correct answer is option 'B'. Can you explain this answer?
Let f(x) = x – [x], then f ‘ (x) = 1 for
a)
all x ∈ I
b)
all x ∈ (R−I)
c)
all x ∈ R
d)
all x ∈ Rx- {0]
|
|
Aman Gupta answered |
Explanation:
To understand the given function f(x) = x [x], let's break it down into two parts:
1. The function [x] represents the greatest integer function, also known as the floor function. It returns the greatest integer less than or equal to x. For example, [2.5] = 2 and [3] = 3.
2. The function x [x] is the product of x and [x]. Therefore, if we substitute a value of x, let's say x = 2.5, then f(2.5) = 2.5 [2.5] = 2.5 * 2 = 5.
Now, let's analyze the options given:
a) all x in I
This option states that the function f(x) = 1 for all x in the set of integers. However, this is not true because the function f(x) = x [x] is a continuous function and takes different values for different values of x.
c) all x in R
This option states that the function f(x) = 1 for all x in the set of real numbers. Again, this is not true because the function f(x) = x [x] takes different values for different values of x.
d) all x in R - {0}
This option states that the function f(x) = 1 for all x in the set of real numbers except 0. However, this is also not true because the function f(x) = x [x] takes different values for different values of x.
Therefore, the correct option is:
b) all x in R
This option states that the function f(x) = 1 for all x in the set of real numbers. This is true because the function f(x) = x [x] takes different values for different values of x, including the case where it equals 1.
In conclusion, the correct answer is option 'B' - all x in R.
Which of the following function is not differentiable at x = 0?- a)x2
- b)|x|
- c)cos x
- d)ax + b
Correct answer is option 'B'. Can you explain this answer?
Which of the following function is not differentiable at x = 0?
a)
x2
b)
|x|
c)
cos x
d)
ax + b
|
|
Swara Kumar answered |
Explanation:
To check the differentiability of a function at a point, we have to check whether the left-hand limit and the right-hand limit of the function exist and are equal or not.
a) x^2 is differentiable at x=0 since its left-hand limit and right-hand limit both exist and are equal to 0.
b) |x| is not differentiable at x=0 since its left-hand limit and right-hand limit are not equal. Left-hand limit = -1 and right-hand limit = 1.
c) cos x is differentiable at x=0 since its left-hand limit and right-hand limit both exist and are equal to 1.
d) ax^b is differentiable at x=0 if b>1 or b is a positive integer. If b=1, then the function is differentiable everywhere. If b<1, then="" the="" function="" is="" not="" differentiable="" at="" x="0.">
Therefore, option B, |x|, is not differentiable at x=0 as its left-hand limit and right-hand limit are not equal.
To check the differentiability of a function at a point, we have to check whether the left-hand limit and the right-hand limit of the function exist and are equal or not.
a) x^2 is differentiable at x=0 since its left-hand limit and right-hand limit both exist and are equal to 0.
b) |x| is not differentiable at x=0 since its left-hand limit and right-hand limit are not equal. Left-hand limit = -1 and right-hand limit = 1.
c) cos x is differentiable at x=0 since its left-hand limit and right-hand limit both exist and are equal to 1.
d) ax^b is differentiable at x=0 if b>1 or b is a positive integer. If b=1, then the function is differentiable everywhere. If b<1, then="" the="" function="" is="" not="" differentiable="" at="" x="0.">
Therefore, option B, |x|, is not differentiable at x=0 as its left-hand limit and right-hand limit are not equal.
The function f (x) = 1 + | sin x l is- a)differentiable everywhere.
- b)continuous everywhere
- c)continuous nowhere
- d)differentiable nowhere
Correct answer is option 'B'. Can you explain this answer?
The function f (x) = 1 + | sin x l is
a)
differentiable everywhere.
b)
continuous everywhere
c)
continuous nowhere
d)
differentiable nowhere

|
Rithika Mishra answered |
f(x) = 1+|sinx| is not derivable at those x for which sinx = 0, however, 1+|sinx| is continuous everywhere (being the sum of two continuous functions)
Derivative of cos  with respect to x is
with respect to x is- a)
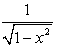
- b)
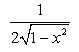
- c)
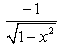
- d)

Correct answer is option 'D'. Can you explain this answer?
Derivative of cos  with respect to x is
with respect to x is
a)
b)
c)
d)

|
Ashim Pattanaik answered |
Let x= cos2A then root of 1+cos2A /2 = cosA .So cos^-1( cosA) =A=(cos^-1 x )/2.Then by using derivative we can find out -1/2root 1-x^2
Find the differential coefficient y = (sec 5x)5x - a)log ( sec 5x) + 5x log (tan 5x)
- b)5(sec 5x)5x [log (sec 5x) + 5x tan 5x ]
- c)(sec 5x)5x [log( sec 5x) + 5x log (tan 5x)]
- d)log (sec 5x) + 5x tan 5x
Correct answer is option 'B'. Can you explain this answer?
Find the differential coefficient y = (sec 5x)5x
a)
log ( sec 5x) + 5x log (tan 5x)
b)
5(sec 5x)5x [log (sec 5x) + 5x tan 5x ]
c)
(sec 5x)5x [log( sec 5x) + 5x log (tan 5x)]
d)
log (sec 5x) + 5x tan 5x

|
Angelica Das answered |
Take log of both sides then differentiate with respect to x. then replace the value of y in the equation
Chapter doubts & questions for Continuity and Differentiability - 6 Months Preparation for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Continuity and Differentiability - 6 Months Preparation for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup

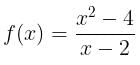
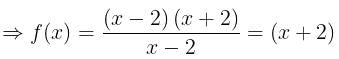 Therefore, f(x) continuous everywhere.
Therefore, f(x) continuous everywhere.