All Exams >
GMAT >
35 Days Preparation for GMAT >
All Questions
All questions of Sequences for GMAT Exam
If S is the infinite sequence S1 = 6, S2 = 12, ..., Sn = Sn-1 + 6,..., what is the sum of all terms in the set {S13, S14, ..., S28}?- a)1800
- b)1845
- c)1890
- d)1968
- e)2016
Correct answer is option 'D'. Can you explain this answer?
If S is the infinite sequence S1 = 6, S2 = 12, ..., Sn = Sn-1 + 6,..., what is the sum of all terms in the set {S13, S14, ..., S28}?
a)
1800
b)
1845
c)
1890
d)
1968
e)
2016

|
Anirban Singh answered |
Sum of the Infinite Sequence
To find the sum of the terms in the set {S13, S14, ..., S28}, we need to first determine the value of S13 and S28.
Given that the sequence is defined as Sn = Sn-1 + 6, we can see that the difference between consecutive terms is 6.
Finding S13 and S28
To find S13, we use the formula Sn = Sn-1 + 6.
S13 = S12 + 6
S13 = 12 + 6
S13 = 18
Similarly, to find S28, we continue the sequence:
S14 = S13 + 6 = 18 + 6 = 24
S15 = S14 + 6 = 24 + 6 = 30
...
S28 = S27 + 6 = 54 + 6 = 60
Calculating the Sum
Now that we have determined the values of S13 and S28, we can find the sum of the terms in the set {S13, S14, ..., S28}:
Sum = S13 + S14 + ... + S28
Sum = 18 + 24 + ... + 60
Sum = 18 + 24 + 30 + ... + 60
This is an arithmetic series with a common difference of 6. We can use the formula for the sum of an arithmetic series to find the total sum:
Sum = n/2 * (first term + last term)
Sum = 16/2 * (18 + 60)
Sum = 8 * 78
Sum = 624
Therefore, the sum of all terms in the set {S13, S14, ..., S28} is 624, which is closest to option D, 1968.
To find the sum of the terms in the set {S13, S14, ..., S28}, we need to first determine the value of S13 and S28.
Given that the sequence is defined as Sn = Sn-1 + 6, we can see that the difference between consecutive terms is 6.
Finding S13 and S28
To find S13, we use the formula Sn = Sn-1 + 6.
S13 = S12 + 6
S13 = 12 + 6
S13 = 18
Similarly, to find S28, we continue the sequence:
S14 = S13 + 6 = 18 + 6 = 24
S15 = S14 + 6 = 24 + 6 = 30
...
S28 = S27 + 6 = 54 + 6 = 60
Calculating the Sum
Now that we have determined the values of S13 and S28, we can find the sum of the terms in the set {S13, S14, ..., S28}:
Sum = S13 + S14 + ... + S28
Sum = 18 + 24 + ... + 60
Sum = 18 + 24 + 30 + ... + 60
This is an arithmetic series with a common difference of 6. We can use the formula for the sum of an arithmetic series to find the total sum:
Sum = n/2 * (first term + last term)
Sum = 16/2 * (18 + 60)
Sum = 8 * 78
Sum = 624
Therefore, the sum of all terms in the set {S13, S14, ..., S28} is 624, which is closest to option D, 1968.
The sum of the squares of the first 15 positive integers (12 + 22 + 32 + . . . + 152) is equal to 1240. What is the sum of the squares of the second 15 positive integers (162 + 172 + 182 + . . . + 302) ?- a)2480
- b)3490
- c)6785
- d)8215
- e)9255
Correct answer is option 'D'. Can you explain this answer?
The sum of the squares of the first 15 positive integers (12 + 22 + 32 + . . . + 152) is equal to 1240. What is the sum of the squares of the second 15 positive integers (162 + 172 + 182 + . . . + 302) ?
a)
2480
b)
3490
c)
6785
d)
8215
e)
9255

|
Nitya Kumar answered |
The key to solving this problem is to represent the sum of the squares of the second 15 integers as follows: (15 + 1)2 + (15 + 2)2 + (15 + 3)2 + . . . + (15 + 15)2.
Recall the popular quadratic form, (a + b)2 = a2 + 2ab + b2. Construct a table that uses this expansion to calculate each component of each term in the series as follows:


In order to calculate the desired sum, we can find the sum of each of the last 3 columns and then add these three subtotals together. Note that since each column follows a simple pattern, we do not have to fill in the whole table, but instead only need to calculate a few terms in order to determine the sums.
The column labeled a2 simply repeats 225 fifteen times; therefore, its sum is 15(225) = 3375.
The column labeled 2ab is an equally spaced series of positive numbers. Recall that the average of such a series is equal to the average of its highest and lowest values; thus, the average term in this series is (30 + 450) / 2 = 240. Since the sum of n numbers in an equally spaced series is simply n times the average of the series, the sum of this series is 15(240) = 3600.
The last column labeled b2 is the sum of the squares of the first 15 integers. This was given to us in the problem as 1240.
Finally, we sum the 3 column totals together to find the sum of the squares of the second 15 integers: 3375 + 3600 + 1240 = 8215. The correct answer choice is (D).
If the sum of the first five terms of an Arithmetic sequence is equal to 120 and the sum of the next five terms of the same Arithmetic Sequence is equal to 245, what is the 4th term of this Sequence?- a)29
- b)34
- c)81
- d)86
- e)91
Correct answer is option 'A'. Can you explain this answer?
If the sum of the first five terms of an Arithmetic sequence is equal to 120 and the sum of the next five terms of the same Arithmetic Sequence is equal to 245, what is the 4th term of this Sequence?
a)
29
b)
34
c)
81
d)
86
e)
91
|
|
Lavanya Menon answered |
Given:
- Sum of the first 5 terms of an arithmetic sequence = 120
- Sum of the next 5 terms of the same arithmetic sequence = 245
- Let the first term of this arithmetic sequence be x1 and let the common difference be d.
To Find:
- 4th term of the arithmetic sequence.
- So the 4th term of the sequence will become x1+3d
- So we need to find the value of x1 and d or the value of x1+3d to find the 4th term of the sequence.
Approach:
- We know that the sum of first n terms of the Arithmetic Sequence is given as
where n is the number of terms in the arithmetic sequence.
- Using the formula above for the sum of first 5 terms of the sequence, we will get an equation in terms of and common difference d, as we are given the sum of first 5 terms of the sequence.
- We are also given the sum of next 5 terms of the sequence. So, we will be able to calculate the sum of first 10 terms of the sequence.
→ Sum of first 10 terms of sequence = Sum of first 5 terms + sum of next 5 terms. - Using the formula above for the sum of first 10 terms of sequence, we will get another equation in terms of x1 and common difference d.
- Using these two equations in x1 and d, we will be able to calculate the value of x1 and d.
- Knowing the values of x1 and d, we will be able to calculate the fourth term of the sequence, which is equal to x1+3d
Working out:
- Sum of first 5 terms of the arithmetic sequence = 120
- Putting this in formula of sum of first n terms, where n=5 and z=120, we get
- Sum of the next 5 terms of the sequence = 245
- Sum of the first 10 terms of the sequence = Sum of the first five terms + Sum of the next five terms.
- Sum of the first 10 terms of the sequence = 120+245 = 365
- Sum of the first 10 terms of the sequence = 120+245 = 365
- Now, using the formula of the sum of first n terms of an arithmetic sequence, we get
- Solving Equations 1 and 2.
- Multiplying ‘equation 1’ by 2, we have 10x1+20d =240 ...(Equation 3)
Now that we have values of x1 and d. The value of 4th term of the sequence will be
⇒ x1+3(d)=14+3(5)=29
Answer:
- The value of 4th term of the sequence is 29.
- Hence the correct answer is option A
Alternate method
- Let the first term be 'a' and common dfference between any two cosecutive terms be 'd'
Therefore,
- 1st term = a
- 5th term = a + 4d
- 6th term = a + 5d
- 10th term = a + 9d
- Average of first five terms of an arithemetic sequence = (First term + Last term)/2 = (a + a +4d) / 2 = a + 2d
- Sum of first five terms = Average of first five terms * 5 = (a + 2d) * 5 = 120
- a + 2d = 120/5 = 24 ---------------- Eq(1)
- Average of next five terms of the arithemetic sequence = (First term + Last term)/2 = (a+ 5d + a +9d) / 2 = a + 7d
- Sum of five terms = Average of five terms * 5 = (a + 7d) * 5 = 245
- a + 7d = 245/5 = 49---------------- Eq(2)
Solving Eq(1) and (2) we get
- d = 5
- 4th term =
- a + 3d = (a+2d)+ d = 24 + 5 = 29
Correct Answer: Option A
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?- a)25
- b)8
- c)6
- d)5
- e)2
Correct answer is option 'C'. Can you explain this answer?
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?
a)
25
b)
8
c)
6
d)
5
e)
2

|
Mihir Nambiar answered |
5! means factorial 25 whose value = 25 * 24 * 23 * 22 *....* 1
When a number that is a multiple of 5 is multiplied with an even number, it results in a trailing zero.
(Product of 5 and 2 is 10 and any number when multiplied with 10 or a power of 10 will have one or as many zeroes as the power of 10 with which it has been multiplied)
(Product of 5 and 2 is 10 and any number when multiplied with 10 or a power of 10 will have one or as many zeroes as the power of 10 with which it has been multiplied)
In 25!, the following numbers have 5 as their factor: 5, 10, 15, 20, and 25.
25 is the square of 5 and hence it has two 5s in it.
In toto, it is equivalent of having six 5s.
25 is the square of 5 and hence it has two 5s in it.
In toto, it is equivalent of having six 5s.
There are at least 6 even numbers in 25!
Hence, the number 25! will have 6 trailing zeroes in it.
Hence, the number 25! will have 6 trailing zeroes in it.
Choice C is the correct answer.
When 242 is divided by a certain divisor the remainder obtained is 8. When 698 is divided by the same divisor the remainder obtained is 9. However, when the sum of the two numbers 242 and 698 is divided by the divisor, the remainder obtained is 4. What is the value of the divisor?- a)11
- b)17
- c)13
- d)23
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
When 242 is divided by a certain divisor the remainder obtained is 8. When 698 is divided by the same divisor the remainder obtained is 9. However, when the sum of the two numbers 242 and 698 is divided by the divisor, the remainder obtained is 4. What is the value of the divisor?
a)
11
b)
17
c)
13
d)
23
e)
None of these

|
Saumya Shah answered |
When 242 is divided by a certain divisor the remainder obtained is 8.
Let the divisor be d.
When 242 is divided by d, let the quotient be 'x'. The remainder is 8.
Therefore, 242 = xd + 8
When 242 is divided by d, let the quotient be 'x'. The remainder is 8.
Therefore, 242 = xd + 8
When 698 is divided by the same divisor the remainder obtained is 9.
Let y be the quotient when 698 is divided by d.
Then, 698 = yd + 9.
Then, 698 = yd + 9.
When the sum of the two numbers, 242 and 698, is divided by the divisor, the remainder obtained is 4.
242 + 698 = 940 = xd + yd + 8 + 9
940 = xd + yd + 17
940 = xd + yd + 17
Because xd and yd are divisible by d, the remainder when 940 is divided by d should have been 17.
However, because we know that the remainder is 4, it would be possible only when 17d17d leaves a remainder of 4.
If the remainder obtained is 4 when 17 is divided by 'd', then 'd' has to be 13.
Choice C is the correct answer.
How many different positive integers exist between 106 and 107, the sum of whose digits is equal to 2?- a)6
- b)7
- c)5
- d)8
- e)18
Correct answer is option 'B'. Can you explain this answer?
How many different positive integers exist between 106 and 107, the sum of whose digits is equal to 2?
a)
6
b)
7
c)
5
d)
8
e)
18

|
Athira Choudhury answered |
Method 1 to solve this GMAT Number Properties Question: Find the number of such integers existing for a lower power of 10 and extrapolate the results.
Between 10 and 100, that is 101 and 102, we have 2 numbers, 11 and 20.
Between 100 and 1000, that is 102 and 103, we have 3 numbers, 101, 110 and 200.
Therefore, between 106 and 107, one will have 7 integers whose sum will be equal to 2.
Between 100 and 1000, that is 102 and 103, we have 3 numbers, 101, 110 and 200.
Therefore, between 106 and 107, one will have 7 integers whose sum will be equal to 2.
Alternative approach
All numbers between 106 and 107 will be 7 digit numbers.
There are two possibilities if the sum of the digits has to be '2'.
There are two possibilities if the sum of the digits has to be '2'.
Possibility 1: Two of the 7 digits are 1s and the remaining 5 are 0s.
The left most digit has to be one of the 1s. That leaves us with 6 places where the second 1 can appear.
So, a total of six 7-digit numbers comprising two 1s exist, sum of whose digits is '2'.
The left most digit has to be one of the 1s. That leaves us with 6 places where the second 1 can appear.
So, a total of six 7-digit numbers comprising two 1s exist, sum of whose digits is '2'.
Possibility 2: One digit is 2 and the remaining are 0s.
The only possibility is 2000000.
The only possibility is 2000000.
Total count is the sum of the counts from these two possibilities = 6 + 1 = 7
Choice B is the correct answer.
The sequence a1, a2,…an is such that an = an-1 +n*d for all n > 1, where d is a positive integer. If a3 = 20 and a5 = 47, what is the value of a7?- a)53
- b)65
- c)75
- d)80
- e)86
Correct answer is option 'E'. Can you explain this answer?
The sequence a1, a2,…an is such that an = an-1 +n*d for all n > 1, where d is a positive integer. If a3 = 20 and a5 = 47, what is the value of a7?
a)
53
b)
65
c)
75
d)
80
e)
86

|
Kavya Chakraborty answered |
Given
- A sequence a1, a2,…an
- an = an-1 +n*d for all n > 1, where d is an integer > 0
- a3 = 20
- a5 = 47
To Find: a7?
Approach
- As an = an-1 +n*d, we can express a7 in terms of a1 and d
- So, we need to find the value of a1 and d.
- As we are given the values of a3 and a5, we will express them in terms of a1 and d to get 2 equations in a1 and d.
- We will then solve these two equations to find out the value of a1 and d.
Working Out
Solving (1) and (2), we have a1 = 5 and d = 3 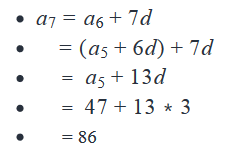
Answer: E
If the sum of the first 30 positive odd integers is k, what is the sum of first 30 non-negative even integers?- a)k-29
- b)k-30
- c)k
- d)k+29
- e)k+30
Correct answer is option 'B'. Can you explain this answer?
If the sum of the first 30 positive odd integers is k, what is the sum of first 30 non-negative even integers?
a)
k-29
b)
k-30
c)
k
d)
k+29
e)
k+30

|
Moumita Sen answered |
Given
- 1 + 3 + 5………..30*2 -1 = k.
- Let’s call this sequence O
To Find: 0 + 2+ 4………30 *2 -2 = ?
- Let’s call this sequence E
Approach
- To express the sum of sequence E in terms of k, we need to express the terms of sequence E in terms of sequence O
- Now, we see that we can write 0 = 1 – 1
- Similarly, we can write 2 = 3 -1
- Continuing the same pattern, we can write 58 = 59 -1
- Observe that 1, 3…..59 are terms of sequence O. So, using the above process we have captured all the terms of sequence O in sequence E
- We will use the above logic to represent the sum of sequence E in terms of k
Working Out
- 0 + 2+ 4……58 = (1-1) + (3-1) +…….(59- 1) = 1+ 3+ 5…….59 – (1 + 1 + 1……….30 times)
- 0 + 2 + 4 …….+ 58 = k – 30
Answer: B
The nth term of an increasing sequence S is given by Sn = Sn-1 + Sn-2 for n > 2 and the nth term of a sequence S’ is given by S’n = S’n-1 - S’n-2 for n > 2. If S5 = S’5, what is the average (arithmetic mean) of S2 and S’2?(1) The difference between the fourth term and the second term of sequence S is 14.(2) The sum of the fourth term and the second term of sequence S’ is 14.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
The nth term of an increasing sequence S is given by Sn = Sn-1 + Sn-2 for n > 2 and the nth term of a sequence S’ is given by S’n = S’n-1 - S’n-2 for n > 2. If S5 = S’5, what is the average (arithmetic mean) of S2 and S’2?
(1) The difference between the fourth term and the second term of sequence S is 14.
(2) The sum of the fourth term and the second term of sequence S’ is 14.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Aarav Sharma answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Increasing sequence S whose nth term is represented as Sn = Sn-1 + Sn-2 for n > 2
- For a sequence S’, the nth term of which is represented as S’n = S’n-1 - S’n-2 for n > 2
- S5 = S’5
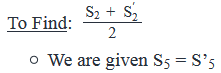
Thus we need to find the value of S3 to find the average of S2 andS′2
Step 3: Analyze Statement 1 independently
(1) The difference between the fourth term and the second term of sequence S is 14
- S4−S2=14
- Substituting the expression of S4=S3+S2
- (S3+S2)−S2=14,i.e.S3=14
As we know the value of S3, the statement is sufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The sum of the fourth term and the second term of sequence S’ is 14.
- S′2+S′4=14
- Substituting the expression of S′4=S′3−S′2
- S′2+(S′3−S′2)=14
- S′3=14
Does not tell us anything about the value of S3, the statement is insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from step -3, this step is not required.
Answer: A
How many integral divisors does the number 120 have?- a)14
- b)16
- c)12
- d)20
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
How many integral divisors does the number 120 have?
a)
14
b)
16
c)
12
d)
20
e)
None of these

|
Nikhil Khanna answered |
Step 1 of solving this GMAT Number Properties Question: Express the number in terms of its prime factors
120 = 23 * 3 * 5.
The three prime factors are 2, 3 and 5.
The powers of these prime factors are 3, 1 and 1 respectively.
The three prime factors are 2, 3 and 5.
The powers of these prime factors are 3, 1 and 1 respectively.
Step 2 of solving this GMAT Number Properties Question:Find the number of factors as follows
To find the number of factors / integral divisors that 120 has, increment the powers of each of the prime factors by 1 and then multiply them.
Number of factors = (3 + 1) * (1 + 1) * (1 + 1) = 4 * 2 * 2 =16
Choice B is the correct answer.
For any integer k from 1 to 10, inclusive, the kth of a certain sequence is given by [(-1)(k+1)] × (1 / 2k). If T is the sum of the first 10 terms of the sequence, then T is:- a)greater than 2
- b)between 1 and 2
- c)between 1/2 and 1
- d)between 1/4 and ½
- e)less than 1/4
Correct answer is option 'D'. Can you explain this answer?
For any integer k from 1 to 10, inclusive, the kth of a certain sequence is given by [(-1)(k+1)] × (1 / 2k). If T is the sum of the first 10 terms of the sequence, then T is:
a)
greater than 2
b)
between 1 and 2
c)
between 1/2 and 1
d)
between 1/4 and ½
e)
less than 1/4

|
Soumya Iyer answered |
T= 1/2-1/22+1/23-...-1/210
= 1/4+1/42+1/43+1/44+1/45
Notice that 1/42+1/43+1/44+1/45 < 1/4, we can say that 1/4<T<1/2.
Answer is D
= 1/4+1/42+1/43+1/44+1/45
Notice that 1/42+1/43+1/44+1/45 < 1/4, we can say that 1/4<T<1/2.
Answer is D
Sequence S is defined as Sn = 2Sn-1 – 2. If S1 = 3, then S10 – S9 =- a)2
- b)120
- c)128
- d)250
- e)256
Correct answer is option 'E'. Can you explain this answer?
Sequence S is defined as Sn = 2Sn-1 – 2. If S1 = 3, then S10 – S9 =
a)
2
b)
120
c)
128
d)
250
e)
256

|
Kavya Chakraborty answered |
To find the explicit formula for the sequence S, we need to know the value of the first term, S₁. Without that information, we cannot determine the explicit formula.
Please provide the value of S₁, or any other information about the sequence, so that we can help you find the explicit formula.
Please provide the value of S₁, or any other information about the sequence, so that we can help you find the explicit formula.
If both 112 and 33 are factors of the number a * 43 * 62 * 1311, then what is the smallest possible value of 'a'?- a)121
- b)3267
- c)363
- d)33
- e)None of the above
Correct answer is option 'C'. Can you explain this answer?
If both 112 and 33 are factors of the number a * 43 * 62 * 1311, then what is the smallest possible value of 'a'?
a)
121
b)
3267
c)
363
d)
33
e)
None of the above

|
Snehal Banerjee answered |
Explanation:
Factors of the given number:
- The given number is a * 43 * 62 * 1311.
- Factors of 43: 1, 43.
- Factors of 62: 1, 2, 31, 62.
- Factors of 1311: 1, 3, 19, 69, 131, 393, 873, 1311.
Common factors:
- Factors of 112: 1, 2, 4, 7, 8, 14, 16, 28, 56, 112.
- Factors of 33: 1, 3, 11, 33.
Smallest possible value of a:
- To find the smallest possible value of 'a', we need to consider the common factors of 112 and 33.
- The common factors of 112 and 33 are 1 and 7.
- So, the smallest possible value of 'a' can be obtained by multiplying 1 and 7 i.e. 7.
Therefore, the smallest possible value of 'a' is 7, which is not provided in the options. Hence, the correct answer is option 'e) None of the above'.
Factors of the given number:
- The given number is a * 43 * 62 * 1311.
- Factors of 43: 1, 43.
- Factors of 62: 1, 2, 31, 62.
- Factors of 1311: 1, 3, 19, 69, 131, 393, 873, 1311.
Common factors:
- Factors of 112: 1, 2, 4, 7, 8, 14, 16, 28, 56, 112.
- Factors of 33: 1, 3, 11, 33.
Smallest possible value of a:
- To find the smallest possible value of 'a', we need to consider the common factors of 112 and 33.
- The common factors of 112 and 33 are 1 and 7.
- So, the smallest possible value of 'a' can be obtained by multiplying 1 and 7 i.e. 7.
Therefore, the smallest possible value of 'a' is 7, which is not provided in the options. Hence, the correct answer is option 'e) None of the above'.
If integer k is equal to the sum of all even multiples of 15 between 295 and 615, what is the greatest prime factor of k?- a)5
- b)7
- c)11
- d)13
- e)17
Correct answer is option 'C'. Can you explain this answer?
If integer k is equal to the sum of all even multiples of 15 between 295 and 615, what is the greatest prime factor of k?
a)
5
b)
7
c)
11
d)
13
e)
17

|
Sahana Mehta answered |
To find the sum of all even multiples of 15 between 295 and 615, we need to find the first and last even multiples of 15 in this range and then use the formula for the sum of an arithmetic series.
Finding the first even multiple of 15:
The smallest multiple of 15 in the range is 300, which is divisible by 2 and therefore an even number.
Finding the last even multiple of 15:
The largest multiple of 15 in the range is 600. However, 600 is not an even number, so we need to find the largest even multiple of 15 that is less than or equal to 600. Dividing 600 by 15, we get 40, so the largest even multiple of 15 that is less than or equal to 600 is 40 * 15 = 600.
Finding the number of terms in the series:
To find the number of terms in the series, we use the formula:
number of terms = (last term - first term) / common difference + 1
In this case, the first term is 300, the last term is 600, and the common difference is 30 (since each term is obtained by adding 30 to the previous term). Plugging these values into the formula, we get:
number of terms = (600 - 300) / 30 + 1 = 10 + 1 = 11
Calculating the sum of the series:
The sum of an arithmetic series can be found using the formula:
sum = (number of terms / 2) * (first term + last term)
In this case, the number of terms is 11, the first term is 300, and the last term is 600. Plugging these values into the formula, we get:
sum = (11 / 2) * (300 + 600) = 5.5 * 900 = 4950
Therefore, the sum of all even multiples of 15 between 295 and 615 is 4950.
Finding the greatest prime factor of k:
To find the greatest prime factor of 4950, we can factorize it. The prime factorization of 4950 is:
4950 = 2 * 3 * 3 * 5 * 5 * 11
The greatest prime factor is 11.
Therefore, the greatest prime factor of k is 11, which corresponds to option C.
Finding the first even multiple of 15:
The smallest multiple of 15 in the range is 300, which is divisible by 2 and therefore an even number.
Finding the last even multiple of 15:
The largest multiple of 15 in the range is 600. However, 600 is not an even number, so we need to find the largest even multiple of 15 that is less than or equal to 600. Dividing 600 by 15, we get 40, so the largest even multiple of 15 that is less than or equal to 600 is 40 * 15 = 600.
Finding the number of terms in the series:
To find the number of terms in the series, we use the formula:
number of terms = (last term - first term) / common difference + 1
In this case, the first term is 300, the last term is 600, and the common difference is 30 (since each term is obtained by adding 30 to the previous term). Plugging these values into the formula, we get:
number of terms = (600 - 300) / 30 + 1 = 10 + 1 = 11
Calculating the sum of the series:
The sum of an arithmetic series can be found using the formula:
sum = (number of terms / 2) * (first term + last term)
In this case, the number of terms is 11, the first term is 300, and the last term is 600. Plugging these values into the formula, we get:
sum = (11 / 2) * (300 + 600) = 5.5 * 900 = 4950
Therefore, the sum of all even multiples of 15 between 295 and 615 is 4950.
Finding the greatest prime factor of k:
To find the greatest prime factor of 4950, we can factorize it. The prime factorization of 4950 is:
4950 = 2 * 3 * 3 * 5 * 5 * 11
The greatest prime factor is 11.
Therefore, the greatest prime factor of k is 11, which corresponds to option C.
What is the sixtieth term in the following sequence? 1, 2, 4, 7, 11, 16, 22...- a)1671
- b)1760
- c)1761
- d)1771
- e)1821
Correct answer is option 'D'. Can you explain this answer?
What is the sixtieth term in the following sequence? 1, 2, 4, 7, 11, 16, 22...
a)
1671
b)
1760
c)
1761
d)
1771
e)
1821

|
Athul Joshi answered |
Noting that a1 = 1, each subsequent term can be calculated as follows:
a1 = 1
a2 = a1 + 1
a3 = a1 + 1 + 2
a4 = a1 + 1 + 2 + 3
ai = a1 + 1 + 2 + 3 + ... + i-1
a1 = 1
a2 = a1 + 1
a3 = a1 + 1 + 2
a4 = a1 + 1 + 2 + 3
ai = a1 + 1 + 2 + 3 + ... + i-1
In other words, ai = a1 plus the sum of the first i - 1 positive integers. In order to determine the sum of the first i - 1 positive integers, find the sum of the first and last terms, which would be 1 and i - 1 respectively, plus the sum of the second and penultimate terms, and so on, while working towards the median of the set. Note that the sum of each pair is always equal to i:
1 + (i - 1) = i
2 + (i – 2) = i
3 + (i – 3) = i
…
2 + (i – 2) = i
3 + (i – 3) = i
…
Because there are (i - 1)/2 such pairs in a set of i - 1 consecutive integers, this operation can be summarized by the formula i(i - 1)/2. For this problem, substituting a1 = 1 and using this formula for the sum of the first (i-1) integers yields:
ai = 1 + (i)(i - 1)/2
ai = 1 + (i)(i - 1)/2
The sixtieth term can be calculated as:
a60 = 1 + (59)(60)/2
a60 = 1,771
a60 = 1 + (59)(60)/2
a60 = 1,771
The correct answer is D.
A number when divided by a divisor leaves a remainder of 24. When twice the original number is divided by the same divisor, the remainder is 11. What is the value of the divisor?- a)13
- b)59
- c)35
- d)37
- e)12
Correct answer is option 'D'. Can you explain this answer?
A number when divided by a divisor leaves a remainder of 24. When twice the original number is divided by the same divisor, the remainder is 11. What is the value of the divisor?
a)
13
b)
59
c)
35
d)
37
e)
12

|
Moumita Sen answered |
Step 1 of solving this GMAT Number Properties Question: Decode "A number when divided by a divisor leaves a remainder of 24"
Let the original number be 'a'.
Let the divisor be 'd'.
Let the quotient of dividing 'a' by 'd' be 'x'.
Therefore, we can write the division as a/d = x
Let the divisor be 'd'.
Let the quotient of dividing 'a' by 'd' be 'x'.
Therefore, we can write the division as a/d = x
and the remainder is 24.
i.e., a = dx + 24
i.e., a = dx + 24
Step 2 of solving this GMAT Number Properties Question: Decode "When twice the original number is divided by the same divisor, the remainder is 11"
Twice the original number is divided by 'd' means 2a is divided by d.
We know from Step 1 that a = dx + 24.
Therefore, 2a = 2(dx + 48) or 2a = 2dx + 48
We know from Step 1 that a = dx + 24.
Therefore, 2a = 2(dx + 48) or 2a = 2dx + 48
When (2dx + 48) is divided by 'd' the remainder is 11.
2dx is divisible by 'd' and will therefore, not leave a remainder.
The remainder of 11 would be the remainder of dividing 48 by d.
2dx is divisible by 'd' and will therefore, not leave a remainder.
The remainder of 11 would be the remainder of dividing 48 by d.
The question essentially becomes "What number will leave a remainder of 11 when it divides 48?"
When 37 divides 48, the remainder is 11.
When 37 divides 48, the remainder is 11.
Hence, the divisor is 37.
Choice D is the correct answer.
The infinite sequence Sk is defined as Sk = 10 Sk – 1 + k, for all k > 1. The infinite sequence An is defined as An = 10 An – 1 + (A1 – (n - 1)), for all n > 1. q is the sum of Sk and An. If S1 = 1 and A1 = 9, and if An is positive, what is the maximum value of k + n when the sum of the digits of q is equal to 9?- a)6
- b)9
- c)12
- d)16
- e)18
Correct answer is option 'E'. Can you explain this answer?
The infinite sequence Sk is defined as Sk = 10 Sk – 1 + k, for all k > 1. The infinite sequence An is defined as An = 10 An – 1 + (A1 – (n - 1)), for all n > 1. q is the sum of Sk and An. If S1 = 1 and A1 = 9, and if An is positive, what is the maximum value of k + n when the sum of the digits of q is equal to 9?
a)
6
b)
9
c)
12
d)
16
e)
18

|
Palak Yadav answered |
Understanding the given sequences:
- The sequence Sk is given by Sk = 10Sk - 1 + k for k > 1.
- The sequence An is given by An = 10An - 1 + (A1 - (n - 1)) for n > 1.
Given initial values:
- S1 = 1
- A1 = 9
Finding the sum q:
- The sum q is defined as the sum of Sk and An.
- q = Sk + An
Finding the sum of the digits of q:
- To find the sum of the digits of q equal to 9, we need to analyze the sequences Sk and An and find the values of k and n that satisfy this condition.
Finding the maximum value of k + n:
- To maximize k + n, we need to find the values of k and n that satisfy the condition of sum of digits of q being 9.
- By analyzing the sequences and applying the given conditions, we can find the maximum value of k + n.
Therefore, after analyzing the sequences and applying the given conditions, we can determine that the maximum value of k + n when the sum of the digits of q is equal to 9 is 18. Hence, the correct answer is option E.
- The sequence Sk is given by Sk = 10Sk - 1 + k for k > 1.
- The sequence An is given by An = 10An - 1 + (A1 - (n - 1)) for n > 1.
Given initial values:
- S1 = 1
- A1 = 9
Finding the sum q:
- The sum q is defined as the sum of Sk and An.
- q = Sk + An
Finding the sum of the digits of q:
- To find the sum of the digits of q equal to 9, we need to analyze the sequences Sk and An and find the values of k and n that satisfy this condition.
Finding the maximum value of k + n:
- To maximize k + n, we need to find the values of k and n that satisfy the condition of sum of digits of q being 9.
- By analyzing the sequences and applying the given conditions, we can find the maximum value of k + n.
Therefore, after analyzing the sequences and applying the given conditions, we can determine that the maximum value of k + n when the sum of the digits of q is equal to 9 is 18. Hence, the correct answer is option E.
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -Q. How many of the numbers x, y, and z are positive if each of these numbers is less than 10?1. x + y + z = 20
2. x + y = 14- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. How many of the numbers x, y, and z are positive if each of these numbers is less than 10?
1. x + y + z = 20
2. x + y = 14
2. x + y = 14
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Srestha Basu answered |
Step 1 of solving this GMAT DS question: Understand the Question Stem
What kind of an answer will the question fetch?
The question is a "How many?" question. For questions asking "how many", the answer should be a number.
The question is a "How many?" question. For questions asking "how many", the answer should be a number.
When is the data sufficient?
The data is sufficient if we are able to get a UNIQUE answer for the number of positive numbers from the information in the statements.
If the statements do not have adequate data to uniquely determine how many among the three numbers are positive, the data is NOT sufficient.
The data is sufficient if we are able to get a UNIQUE answer for the number of positive numbers from the information in the statements.
If the statements do not have adequate data to uniquely determine how many among the three numbers are positive, the data is NOT sufficient.
Key data from the question stem
Each of the three numbers x, y, and z are less than 10.
Each of the three numbers x, y, and z are less than 10.
Step 2 of solving this GMAT DS question:
Evaluate Statement (1) ALONE: x + y + z = 20
Evaluate Statement (1) ALONE: x + y + z = 20
From the question stem we know that each number is less than 10.
So, x < 10, y < 10 and z < 10.
Therefore, the maximum sum of any two of these numbers, say x + y < 20.
So, x < 10, y < 10 and z < 10.
Therefore, the maximum sum of any two of these numbers, say x + y < 20.
However, statement 1 states x + y + z = 20.
Unless the third number, z in this case, is also positive x + y + z cannot be 20.
Hence, we can conclude that all 3 numbers x, y and z are positive.
Unless the third number, z in this case, is also positive x + y + z cannot be 20.
Hence, we can conclude that all 3 numbers x, y and z are positive.
Statement 1 ALONE is sufficient.
Eliminate choices B, C and E. Choices narrow down to A or D.
Eliminate choices B, C and E. Choices narrow down to A or D.
Step 3 of solving this GMAT DS question:
Evaluate Statement (2) ALONE: x + y = 14
Evaluate Statement (2) ALONE: x + y = 14
As each of x and y is less than 10, both x and y have to be positive for the sum to be 14.
However, z could also be positive or z could be negative.
However, z could also be positive or z could be negative.
So, there could be either 2 or 3 positive numbers among the three numbers.
We are not able to find a unique answer from the information in statement 2.
We are not able to find a unique answer from the information in statement 2.
Statement 2 ALONE is NOT sufficient.
Eliminate choice D.
Eliminate choice D.
Statement 1 ALONE is sufficient. Choice A is the answer.
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -Q. When a positive integer 'x' is divided by a divisor 'd', the remainder is 24. What is d?1. When 2x is divided by d, the remainder is 23.
2. When 3x is divided by d, the remainder is 22- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. When a positive integer 'x' is divided by a divisor 'd', the remainder is 24. What is d?
1. When 2x is divided by d, the remainder is 23.
2. When 3x is divided by d, the remainder is 22
2. When 3x is divided by d, the remainder is 22
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Moumita Sen answered |
Step 1 of solving this GMAT DS question: Understand the Question Stem
What kind of an answer will the question fetch?
The question is a "What is the value?" question. For questions asking for a value, the answer should be a number.
The question is a "What is the value?" question. For questions asking for a value, the answer should be a number.
When is the data sufficient?
The data is sufficient if we are able to get a UNIQUE answer for the value of 'd' from the information in the statements.
If either the statements do not have adequate data to determine the value of 'd' or if more than one value of 'd' exists based on the information in the statement, the data is NOT sufficient.
The data is sufficient if we are able to get a UNIQUE answer for the value of 'd' from the information in the statements.
If either the statements do not have adequate data to determine the value of 'd' or if more than one value of 'd' exists based on the information in the statement, the data is NOT sufficient.
What do we know from the question stem?
'x' is a positive integer. Dividing x by d leaves a remainder of 24.
So, the value of 'd' is more than 24.
'x' is a positive integer. Dividing x by d leaves a remainder of 24.
So, the value of 'd' is more than 24.
Step 2 of solving this GMAT DS question:
Evaluate Statement (1) ALONE: When 2x is divided by d, the remainder is 23.
Evaluate Statement (1) ALONE: When 2x is divided by d, the remainder is 23.
The question stem states that when x is divided by d, the remainder is 24.
Therefore, when 2x is divided by d, the remainder should be 2 * 24 = 48.
However, from statement (1) we know that the remainder is 23. We can infer the following from the question stem and statement 1:
Therefore, when 2x is divided by d, the remainder should be 2 * 24 = 48.
However, from statement (1) we know that the remainder is 23. We can infer the following from the question stem and statement 1:
- the divisor d is less than 48
- the divisor is at least 25 and
- 48 divided by divisor d should leave a remainder of 23.
i.e., 48 = nd + 23 or nd = 25.
The possible values for d are 1, 5 and 25.
However, as d is at least 25, the divisor cannot be 1 or 5.
So, we can conclude that 25 is the divisor.
The possible values for d are 1, 5 and 25.
However, as d is at least 25, the divisor cannot be 1 or 5.
So, we can conclude that 25 is the divisor.
Statement 1 ALONE is sufficient.
Eliminate choices B, C and E. Choices narrow down to A or D.
Eliminate choices B, C and E. Choices narrow down to A or D.
Step 3 of solving this GMAT DS question:
Evaluate Statement (2) ALONE: When 3x is divided by d, the remainder is 22.
Evaluate Statement (2) ALONE: When 3x is divided by d, the remainder is 22.
If x leaves a remainder of 24 when divided by d, then 3x will leave a remainder of 3 * 24 = 72 when divided by d.
However, the remainder is 22.
This tells us that the divisor is less than 72 and that 72 divided by d leaves a remainder of 22.
However, the remainder is 22.
This tells us that the divisor is less than 72 and that 72 divided by d leaves a remainder of 22.
So, 72 = n * d + 22
Or nd = 72 - 22 = 50
Or nd = 72 - 22 = 50
If nd = 50, d could be 50 or 25 or 10 or 5 or 2.
However, from the question stem we have deduced that the divisor is at least 25. So, d cannot be 10, 5 and 2.
But, d could be 25 or 50.
However, from the question stem we have deduced that the divisor is at least 25. So, d cannot be 10, 5 and 2.
But, d could be 25 or 50.
From statement 2, we are unable to deduce a unique value for d.
Statement 2 ALONE is NOT sufficient.
Eliminate choice D.
Eliminate choice D.
Statement 1 ALONE is sufficient. Choice A is the answer.
If each term in the sum a1 + a2 + a3 + ... +an is either 7 or 77 and the sum is equal to 350, which of the
following could equal to n?- a)38
- b)39
- c)40
- d)41
- e)42
Correct answer is option 'C'. Can you explain this answer?
If each term in the sum a1 + a2 + a3 + ... +an is either 7 or 77 and the sum is equal to 350, which of the
following could equal to n?
following could equal to n?
a)
38
b)
39
c)
40
d)
41
e)
42

|
Advait Roy answered |
Solution:
To solve this problem, we need to use a bit of logic and guesswork.
Let's start by assuming that all the terms in the sum are 7. In this case, the sum would be:
7 + 7 + 7 + ... + 7 (n terms) = 7n
We know that the sum is 350, so we can set up the equation:
7n = 350
Solving for n, we get:
n = 50
But we also know that each term is either 7 or 77. So let's assume that all the terms are 77. In this case, the sum would be:
77 + 77 + 77 + ... + 77 (n terms) = 77n
We know that the sum is 350, so we can set up the equation:
77n = 350
Solving for n, we get:
n ≈ 4.55
This doesn't give us a whole number for n, so we need to try something in between. Let's assume that half the terms are 7 and half are 77. In this case, the sum would be:
7 + 77 + 7 + 77 + ... (n terms) = (7 + 77)n/2 = 42n
We know that the sum is 350, so we can set up the equation:
42n = 350
Solving for n, we get:
n ≈ 8.33
Again, we don't get a whole number for n. But notice that as we move from all 7s to all 77s to a mix of 7s and 77s, the value of n is decreasing. So we can make an educated guess that the value of n lies somewhere between 50 and 8.
Looking at the answer choices, we see that only option C (40) falls within this range. Therefore, the correct answer is C.
To solve this problem, we need to use a bit of logic and guesswork.
Let's start by assuming that all the terms in the sum are 7. In this case, the sum would be:
7 + 7 + 7 + ... + 7 (n terms) = 7n
We know that the sum is 350, so we can set up the equation:
7n = 350
Solving for n, we get:
n = 50
But we also know that each term is either 7 or 77. So let's assume that all the terms are 77. In this case, the sum would be:
77 + 77 + 77 + ... + 77 (n terms) = 77n
We know that the sum is 350, so we can set up the equation:
77n = 350
Solving for n, we get:
n ≈ 4.55
This doesn't give us a whole number for n, so we need to try something in between. Let's assume that half the terms are 7 and half are 77. In this case, the sum would be:
7 + 77 + 7 + 77 + ... (n terms) = (7 + 77)n/2 = 42n
We know that the sum is 350, so we can set up the equation:
42n = 350
Solving for n, we get:
n ≈ 8.33
Again, we don't get a whole number for n. But notice that as we move from all 7s to all 77s to a mix of 7s and 77s, the value of n is decreasing. So we can make an educated guess that the value of n lies somewhere between 50 and 8.
Looking at the answer choices, we see that only option C (40) falls within this range. Therefore, the correct answer is C.
List A consists of 10 distinct integers arranged in ascending order. Is the difference between the sixth term and the fifth term of list A greater than 5?(1) The difference between any two integers in list A is a multiple of 5.(2) The median of the list is an integer.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
List A consists of 10 distinct integers arranged in ascending order. Is the difference between the sixth term and the fifth term of list A greater than 5?
(1) The difference between any two integers in list A is a multiple of 5.
(2) The median of the list is an integer.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Rhea Gupta answered |
Given:
- List A = {a1, a2, a3, a4, a5, a6, a7, a8, a9, a10}
- consists of all integers,
- where a10 > a9> a8…> a2> a1
To Find: Is a6 – a5 > 5?
Step 4: Analyse Statement 2 independently
The median of the list is an integer.
- Median =?
- List contains 10 elements
- a5 & a6 are integers at the centre of the list (in ascending order)
- Median of the list = a5+a62
-
- = m, where m is an integer
- Rearranging, we get a5+ a6 = 2m = even
- If sum of a6 & a5 is even, then
- Difference of a6 & a5 is also even
- No information about values of the terms , so cannot tell if (a6 – a5) > 5
- Hence, statement 2 is insufficient to answer the question.
Step 5: Analyse Both Statements Together (if needed)
- From statement 1, a6 – a5 = {5, 10, 15}
- From statement 2, a6 – a5 = even
- Combining the two,
- a6 – a5 = even multiples of 5 = {10, 20, 30…}
- a6 – a5 > 5
- So, we can answer the question.
- Hence statement 1 and statement 2 together are sufficient to arrive at a definite answer.
Answer: C
Step 3: Analyse Statement 1 independently
The difference between any two integers in list A is a multiple of 5.
- Difference between any two terms of A can be = {5,10,15…}
- a6 – a5 = {5, 10, 15…}
- Since the difference can also = 5, we cannot be certain that a6 – a5 > 5.
- Hence, Statement 1 is insufficient to answer the question.
Ted and Robin start from the same point at 7 AM and drive in opposite directions. Ted doubles his speed after every 90 minutes whereas Robin reduces her speed by half after every 120 minutes. If Ted starts driving at a speed of 10 kilometers/hour and Robin starts driving at a speed of 120 kilometers/hour, how far in kilometers will they be from one another at 1 PM?- a)195
- b)485
- c)525
- d)645
- e)675
Correct answer is option 'D'. Can you explain this answer?
Ted and Robin start from the same point at 7 AM and drive in opposite directions. Ted doubles his speed after every 90 minutes whereas Robin reduces her speed by half after every 120 minutes. If Ted starts driving at a speed of 10 kilometers/hour and Robin starts driving at a speed of 120 kilometers/hour, how far in kilometers will they be from one another at 1 PM?
a)
195
b)
485
c)
525
d)
645
e)
675

|
Sounak Iyer answered |
To solve this problem, we need to calculate the distances covered by Ted and Robin separately and then find the sum of their distances.
Ted's journey:
Ted doubles his speed after every 90 minutes. So, he will have different speeds during different time intervals.
From 7 AM to 8:30 AM (90 minutes):
Ted's speed = 10 km/hour
Distance covered = Speed × Time = 10 km/hour × 1.5 hours = 15 km
From 8:30 AM to 10 AM (90 minutes):
Ted's speed = 2 × 10 km/hour = 20 km/hour
Distance covered = Speed × Time = 20 km/hour × 1.5 hours = 30 km
From 10 AM to 11:30 AM (90 minutes):
Ted's speed = 2 × 20 km/hour = 40 km/hour
Distance covered = Speed × Time = 40 km/hour × 1.5 hours = 60 km
From 11:30 AM to 1 PM (90 minutes):
Ted's speed = 2 × 40 km/hour = 80 km/hour
Distance covered = Speed × Time = 80 km/hour × 1.5 hours = 120 km
Total distance covered by Ted = 15 km + 30 km + 60 km + 120 km = 225 km
Robin's journey:
Robin reduces her speed by half after every 120 minutes. So, she will have different speeds during different time intervals.
From 7 AM to 9 AM (120 minutes):
Robin's speed = 120 km/hour
Distance covered = Speed × Time = 120 km/hour × 2 hours = 240 km
From 9 AM to 11 AM (120 minutes):
Robin's speed = 120 km/hour ÷ 2 = 60 km/hour
Distance covered = Speed × Time = 60 km/hour × 2 hours = 120 km
From 11 AM to 1 PM (120 minutes):
Robin's speed = 60 km/hour ÷ 2 = 30 km/hour
Distance covered = Speed × Time = 30 km/hour × 2 hours = 60 km
Total distance covered by Robin = 240 km + 120 km + 60 km = 420 km
Total distance between Ted and Robin at 1 PM = Distance covered by Ted + Distance covered by Robin = 225 km + 420 km = 645 km
Therefore, the correct answer is option D) 645 km.
Ted's journey:
Ted doubles his speed after every 90 minutes. So, he will have different speeds during different time intervals.
From 7 AM to 8:30 AM (90 minutes):
Ted's speed = 10 km/hour
Distance covered = Speed × Time = 10 km/hour × 1.5 hours = 15 km
From 8:30 AM to 10 AM (90 minutes):
Ted's speed = 2 × 10 km/hour = 20 km/hour
Distance covered = Speed × Time = 20 km/hour × 1.5 hours = 30 km
From 10 AM to 11:30 AM (90 minutes):
Ted's speed = 2 × 20 km/hour = 40 km/hour
Distance covered = Speed × Time = 40 km/hour × 1.5 hours = 60 km
From 11:30 AM to 1 PM (90 minutes):
Ted's speed = 2 × 40 km/hour = 80 km/hour
Distance covered = Speed × Time = 80 km/hour × 1.5 hours = 120 km
Total distance covered by Ted = 15 km + 30 km + 60 km + 120 km = 225 km
Robin's journey:
Robin reduces her speed by half after every 120 minutes. So, she will have different speeds during different time intervals.
From 7 AM to 9 AM (120 minutes):
Robin's speed = 120 km/hour
Distance covered = Speed × Time = 120 km/hour × 2 hours = 240 km
From 9 AM to 11 AM (120 minutes):
Robin's speed = 120 km/hour ÷ 2 = 60 km/hour
Distance covered = Speed × Time = 60 km/hour × 2 hours = 120 km
From 11 AM to 1 PM (120 minutes):
Robin's speed = 60 km/hour ÷ 2 = 30 km/hour
Distance covered = Speed × Time = 30 km/hour × 2 hours = 60 km
Total distance covered by Robin = 240 km + 120 km + 60 km = 420 km
Total distance between Ted and Robin at 1 PM = Distance covered by Ted + Distance covered by Robin = 225 km + 420 km = 645 km
Therefore, the correct answer is option D) 645 km.
In a certain sequence, every term after the first is determined by multiplying the previous term by an integerconstant greater than 1. If the fifth term of the sequence is less than 1000, what is the maximum number ofnonnegative integer values possible for the first term?- a)60
- b)61
- c)62
- d)63
- e)64
Correct answer is option 'D'. Can you explain this answer?
In a certain sequence, every term after the first is determined by multiplying the previous term by an integerconstant greater than 1. If the fifth term of the sequence is less than 1000, what is the maximum number ofnonnegative integer values possible for the first term?
a)
60
b)
61
c)
62
d)
63
e)
64

|
Arnab Kumar answered |
Problem Analysis:
We are given that every term after the first term in a sequence is determined by multiplying the previous term by an integer constant greater than 1. We need to find the maximum number of nonnegative integer values possible for the first term.
Key Points:
- The first term in the sequence is denoted as 'a'.
- The second term in the sequence is 'a * k', where 'k' is the integer constant greater than 1.
- The third term in the sequence is 'a * k * k'.
- Similarly, the nth term in the sequence is 'a * k^(n-1)'.
Solution:
To find the maximum number of nonnegative integer values possible for the first term, we need to find the largest possible value of 'a' such that the fifth term in the sequence is less than 1000.
Let's calculate the fifth term:
- The fifth term = 'a * k^(5-1)' = 'a * k^4'.
We are given that the fifth term is less than 1000, so we can write the inequality:
a * k^4 < />
Step 1: Calculate the maximum value of 'k':
To maximize the number of nonnegative integer values for 'a', we need to minimize the value of 'k'. Therefore, we should choose the smallest possible value of 'k' such that the inequality holds.
Let's assume the smallest possible value of 'k' to be 2:
a * 2^4 < />
16a < />
a < />
Step 2: Calculate the maximum number of nonnegative integer values for 'a':
The largest possible value of 'a' that satisfies the inequality a < 62.5="" is="" />
Therefore, the maximum number of nonnegative integer values for 'a' is 63 (including 0).
Hence, the correct answer is option D) 63.
We are given that every term after the first term in a sequence is determined by multiplying the previous term by an integer constant greater than 1. We need to find the maximum number of nonnegative integer values possible for the first term.
Key Points:
- The first term in the sequence is denoted as 'a'.
- The second term in the sequence is 'a * k', where 'k' is the integer constant greater than 1.
- The third term in the sequence is 'a * k * k'.
- Similarly, the nth term in the sequence is 'a * k^(n-1)'.
Solution:
To find the maximum number of nonnegative integer values possible for the first term, we need to find the largest possible value of 'a' such that the fifth term in the sequence is less than 1000.
Let's calculate the fifth term:
- The fifth term = 'a * k^(5-1)' = 'a * k^4'.
We are given that the fifth term is less than 1000, so we can write the inequality:
a * k^4 < />
Step 1: Calculate the maximum value of 'k':
To maximize the number of nonnegative integer values for 'a', we need to minimize the value of 'k'. Therefore, we should choose the smallest possible value of 'k' such that the inequality holds.
Let's assume the smallest possible value of 'k' to be 2:
a * 2^4 < />
16a < />
a < />
Step 2: Calculate the maximum number of nonnegative integer values for 'a':
The largest possible value of 'a' that satisfies the inequality a < 62.5="" is="" />
Therefore, the maximum number of nonnegative integer values for 'a' is 63 (including 0).
Hence, the correct answer is option D) 63.
Mike took 5 mock tests before appearing for the GMAT. In each mock test he scored 10 points more than the previous mock test. If he scored 760 on the GMAT and his average score for the mocks was 720, what is the difference between his last mock score and his GMAT score?- a)10
- b)20
- c)30
- d)40
- e)50
Correct answer is option 'B'. Can you explain this answer?
Mike took 5 mock tests before appearing for the GMAT. In each mock test he scored 10 points more than the previous mock test. If he scored 760 on the GMAT and his average score for the mocks was 720, what is the difference between his last mock score and his GMAT score?
a)
10
b)
20
c)
30
d)
40
e)
50

|
Rhea Gupta answered |
Given
Mike took 5 mock tests
- Let his score in the 1st mock be x.
- So, his scores in the other mocks = x+ 10, x+20, x+30, x + 40
- Mike’s score on GMAT = 760
- Average score of mocks = 720
To Find:
- 760 – (x +40)
Working Out
Average score of mocks = (x + x + 10 + … x + 40) /5 = (5x + 100)/5 = x + 20
(The other way to think about this is, as Mike’s scores in the mocks are in arithmetic sequence, average will be the middle term)
(The other way to think about this is, as Mike’s scores in the mocks are in arithmetic sequence, average will be the middle term)
- Mike’s average score in the mocks = x + 20 = 720
- x = 700
Therefore
- x + 40 = 740
- 760 – (x+40) = 760 – 740 = 20
Correct Answer: Option B
In an increasing sequence of 5 consecutive even integers, the sum of the second, third, and fourth integer is 132. What is the sum of the first and last integers?- a)84
- b)86
- c)88
- d)90
- e)92
Correct answer is option 'C'. Can you explain this answer?
In an increasing sequence of 5 consecutive even integers, the sum of the second, third, and fourth integer is 132. What is the sum of the first and last integers?
a)
84
b)
86
c)
88
d)
90
e)
92

|
Chirag Sen answered |
Let the five consecutive even integers be represented by x, x + 2, x + 4, x + 6, and x + 8. Thus, the second, third, and fourth integers are x + 2, x + 4, and x + 6. Since the sum of these three integers is 132, it follows that
3x + 12 = 132, so
3x = 120, and
x = 40.
3x + 12 = 132, so
3x = 120, and
x = 40.
The first integer in the sequence is 40 and the last integer in the sequence is x + 8, or 48.
The sum of 40 and 48 is 88.
The correct answer is C.
What is the remainder when 1044 * 1047 * 1050 * 1053 is divided by 33?- a)3
- b)27
- c)30
- d)21
- e)18
Correct answer is option 'C'. Can you explain this answer?
What is the remainder when 1044 * 1047 * 1050 * 1053 is divided by 33?
a)
3
b)
27
c)
30
d)
21
e)
18

|
Manasa Gupta answered |
You can solve this problem if you know this rule about remainders.
Let a number x divide the product of A and B.
The remainder will be the product of the remainders when x divides A and when x divides B.
Let a number x divide the product of A and B.
The remainder will be the product of the remainders when x divides A and when x divides B.
Using this rule,
The remainder when 33 divides 1044 is 21.
The remainder when 33 divides 1047 is 24.
The remainder when 33 divides 1050 is 27.
The remainder when 33 divides 1053 is 30.
The remainder when 33 divides 1044 is 21.
The remainder when 33 divides 1047 is 24.
The remainder when 33 divides 1050 is 27.
The remainder when 33 divides 1053 is 30.
∴ the remainder when 33 divides 1044 * 1047 * 1050 * 1053 is 21 * 24 * 27 * 30.
Note: The remainder when a number is divided by a divisor 'd' will take values from 0 to (d - 1). It will not be equal to or more than 'd'.
The value of 21 * 24 * 27 * 30 is more than 33.
When the value of the remainder is more than the divisor, the final remainder will be the remainder of dividing the product by the divisor.
i.e., the final remainder is the remainder when 33 divides 21 * 24 * 27 * 30.
When 33 divides 21 * 24 * 27 * 30, the remainder is 30.
The value of 21 * 24 * 27 * 30 is more than 33.
When the value of the remainder is more than the divisor, the final remainder will be the remainder of dividing the product by the divisor.
i.e., the final remainder is the remainder when 33 divides 21 * 24 * 27 * 30.
When 33 divides 21 * 24 * 27 * 30, the remainder is 30.
Choice C is the correct answer.
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?- a)1
- b)2
- c)4
- d)6
- e)9
Correct answer is option 'C'. Can you explain this answer?
S is the infinite sequence S1 = 2, S2 = 22, S3 = 222,...Sk = Sk–1 + 2(10k–1). If p is the sum of the first 30 terms of S, what is the eleventh digit of p, counting right to left from the units digit?
a)
1
b)
2
c)
4
d)
6
e)
9

|
Nilotpal Sen answered |
To find the value of Sk, let's look for a pattern in the sequence.
S1 = 2
S2 = 22
S3 = 222
...
From the given examples, we can see that each term Sk is formed by concatenating the number 2 a total of k times.
So, the pattern is that Sk is the number 2 repeated k times.
Therefore, Sk = 2 repeated k times.
For example:
S4 = 2222
S5 = 22222
and so on.
So, S is an infinite sequence where Sk = 2 repeated k times.
S1 = 2
S2 = 22
S3 = 222
...
From the given examples, we can see that each term Sk is formed by concatenating the number 2 a total of k times.
So, the pattern is that Sk is the number 2 repeated k times.
Therefore, Sk = 2 repeated k times.
For example:
S4 = 2222
S5 = 22222
and so on.
So, S is an infinite sequence where Sk = 2 repeated k times.
Sequence S is defined as Sn = X + (1/X), where X = Sn – 1 + 1, for all n > 1.
If S1= 201, then which of the following must be true of Q, the sum of the first 50 terms of S?- a)13,000 < Q < 14,000
- b)12,000 < Q < 13,000
- c)11,000 < Q < 12,000
- d)10,000 < Q < 11,000
- e)9,000 < Q < 10,000
Correct answer is option 'C'. Can you explain this answer?
Sequence S is defined as Sn = X + (1/X), where X = Sn – 1 + 1, for all n > 1.
If S1= 201, then which of the following must be true of Q, the sum of the first 50 terms of S?
If S1= 201, then which of the following must be true of Q, the sum of the first 50 terms of S?
a)
13,000 < Q < 14,000
b)
12,000 < Q < 13,000
c)
11,000 < Q < 12,000
d)
10,000 < Q < 11,000
e)
9,000 < Q < 10,000

|
Kavya Chakraborty answered |
In this sequence, each term Sn is defined as the reciprocal of the previous term X. The value of X is equal to the previous term Sn.
Let's start with the first term, S1. Since there is no previous term, we can assign any value to it. Let's say S1 = 1.
Now, we can calculate the value of S2 using the formula Sn = X (1/X), where X = Sn.
S2 = X (1/X)
S2 = S1 (1/S1)
S2 = 1 (1/1)
S2 = 1
Similarly, we can calculate the value of S3 using the same formula, but with X = S2.
S3 = X (1/X)
S3 = S2 (1/S2)
S3 = 1 (1/1)
S3 = 1
Continuing this pattern, we can see that all the terms in the sequence will be equal to 1. So, the sequence S is a constant sequence with all terms equal to 1.
Let's start with the first term, S1. Since there is no previous term, we can assign any value to it. Let's say S1 = 1.
Now, we can calculate the value of S2 using the formula Sn = X (1/X), where X = Sn.
S2 = X (1/X)
S2 = S1 (1/S1)
S2 = 1 (1/1)
S2 = 1
Similarly, we can calculate the value of S3 using the same formula, but with X = S2.
S3 = X (1/X)
S3 = S2 (1/S2)
S3 = 1 (1/1)
S3 = 1
Continuing this pattern, we can see that all the terms in the sequence will be equal to 1. So, the sequence S is a constant sequence with all terms equal to 1.
An increasing sequence consists of 4 negative integers and 6 positive integers. Is the sum of the sequence positive?(1) The difference between any two consecutive negative integers is 5 and the difference between any two consecutive positive integers is 2(2) The first term of the sequence is -16- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
An increasing sequence consists of 4 negative integers and 6 positive integers. Is the sum of the sequence positive?
(1) The difference between any two consecutive negative integers is 5 and the difference between any two consecutive positive integers is 2
(2) The first term of the sequence is -16
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Kirti Roy answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Let the sequence be
where
To Find: Is 
Step 3: Analyze Statement 1 independently
(1) The difference between any two consecutive negative integers is 5 and the difference between any two consecutive positive integers is 2
Need to know the value of a1 and a5 to know if the sum of the sequence is greater than 0.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The first term of the sequence is -16
- a1=−16
- We do not know the difference between consecutive terms
Hence,
- Statement 2 alone is not sufficient
Step 5: Analyze Both Statements Together (if needed)
From Statement 1 we got
From Statement 2 we got
- a1 = -16
Combining both we get:
Now, if we notice carefully a5 is a positive integer,
- a5 ≥ 1
Therefore
- 6a5≥6
Hence
- 6a5−4 is always greater than zero.
Combining both statements was sufficient to answer the question
Correct Answer: C
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -Q.
Is x3 > x2?1. x > 0
2. x < 1Numbers: All numbers used are real numbers.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q.
Is x3 > x2?
Is x3 > x2?
1. x > 0
2. x < 1
2. x < 1
Numbers: All numbers used are real numbers.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Saumya Shah answered |
Step 1 of solving this GMAT DS question: Understand the question stem and when the data is sufficient
What kind of an answer will the question fetch?
The question is an "Is" question. Answer to an "is" question is either YES or NO.
The question is an "Is" question. Answer to an "is" question is either YES or NO.
When is the data sufficient?
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
If from the statements we get an answer that x3 > x2 in some instances and it is otherwise in other instances, the data is NOT sufficient.
Step 2 of solving this GMAT DS question: Evaluate Statement (1) ALONE
Statement 1: x > 0
Statement 1: x > 0
We know that x is a positive number.
Interval 1: If 0 < x < 1, then x3 < x2.
For example, (0.5)3 = 0.125, which is lesser than (0.5)2 = 0.25
The answer to the question is NO.
For example, (0.5)3 = 0.125, which is lesser than (0.5)2 = 0.25
The answer to the question is NO.
Interval 2: If x > 1, then x3 > x2
For example, 23 = 8 which is greater than 22 = 4
The answer to the question is YES.
We do NOT have a DEFINITE answer using statement 1.
For example, 23 = 8 which is greater than 22 = 4
The answer to the question is YES.
We do NOT have a DEFINITE answer using statement 1.
Statement 1 ALONE is NOT sufficient.
Eliminate choices A and D. Choices narrow down to B, C or E.
Eliminate choices A and D. Choices narrow down to B, C or E.
Step 3 of solving this GMAT DS question: Evaluate Statement (2) ALONE
Statement 2: x < 1
Statement 2: x < 1
Interval 1: For positive values of x, i.e., 0 < x < 1, we know x3 < x2.
The answer to the question is NO.
The answer to the question is NO.
Interval 2:For negative values of x, x3 will be a negative number and x2 will be a positive number.
Hence, x3 < x2
The answer to the question is NO.
Hence, x3 < x2
The answer to the question is NO.
Lastly, what is the answer if x = 0?
When x = 0, x3 = x2.
The answer to the question is NO.
When x = 0, x3 = x2.
The answer to the question is NO.
Hence, if we know that x < 1, we can conclude that x3 is NOT GREATER THAN x2.
We have a DEFINITE answer, even if it is NO.
We have a DEFINITE answer, even if it is NO.
Statement 2 ALONE is sufficient. Eliminate choices C and E.
Choice B is the answer.
What is the sum of the multiples of 7 from 84 to 140, inclusive?- a)896
- b)963
- c)1008
- d)1792
- e)2016
Correct answer is option 'C'. Can you explain this answer?
What is the sum of the multiples of 7 from 84 to 140, inclusive?
a)
896
b)
963
c)
1008
d)
1792
e)
2016

|
Nandita Chauhan answered |
84 is the 12th multiple of 7. (12 x 7 = 84)
140 is the 20th multiple of 7.
The question is asking us to sum the 12th through the 20th multiples of 7.
The sum of a set = (the mean of the set) x (the number of terms in the set)
There are 9 terms in the set: 20th - 12th + 1 = 8 + 1 = 9
The mean of the set = (the first term + the last term) divided by 2: (84 + 140)/2 = 112
The sum of this set = 112 x 9 = 1008
Alternatively, one could list all nine terms in this set (84, 91, 98 ... 140) and add them.
When adding a number of terms, try to combine terms in a way that makes the addition easier
(i.e. 98 + 112 = 210, 119 + 91 = 210, etc).
The correct answer is C.
140 is the 20th multiple of 7.
The question is asking us to sum the 12th through the 20th multiples of 7.
The sum of a set = (the mean of the set) x (the number of terms in the set)
There are 9 terms in the set: 20th - 12th + 1 = 8 + 1 = 9
The mean of the set = (the first term + the last term) divided by 2: (84 + 140)/2 = 112
The sum of this set = 112 x 9 = 1008
Alternatively, one could list all nine terms in this set (84, 91, 98 ... 140) and add them.
When adding a number of terms, try to combine terms in a way that makes the addition easier
(i.e. 98 + 112 = 210, 119 + 91 = 210, etc).
The correct answer is C.
How many keystrokes are needed to type numbers from 1 to 1000?- a)3001
- b)2893
- c)2704
- d)2890
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
How many keystrokes are needed to type numbers from 1 to 1000?
a)
3001
b)
2893
c)
2704
d)
2890
e)
None of these

|
Mehul Nair answered |
While typing numbers from 1 to 1000, there are 9 single digit numbers: from 1 to 9.
Each of these numbers requires one keystroke.
That is 9 key strokes.
Each of these numbers requires one keystroke.
That is 9 key strokes.
There are 90 two-digit numbers: from 10 to 99.
Each of these numbers requires 2 keystrokes.
Therefore, 180 keystrokes to type the 2-digit numbers.
Each of these numbers requires 2 keystrokes.
Therefore, 180 keystrokes to type the 2-digit numbers.
There are 900 three-digit numbers: from 100 to 999.
Each of these numbers requires 3 keystrokes.
Therefore, 2700 keystrokes to type the 3-digit numbers.
Each of these numbers requires 3 keystrokes.
Therefore, 2700 keystrokes to type the 3-digit numbers.
1000 is a four-digit number which requires 4 keystrokes.
Totally, therefore, one requires 9 + 180 + 2700 + 4 = 2893 keystrokes.
Choice B is the correct answer.
An arithmetic sequence is a sequence in which each term after the first is equal to the sum of the preceding term and a constant, which is also known as the common difference of that arithmetic sequence. An increasing arithmetic sequence N consists of a set of distinct negative integers and an increasing arithmetic sequence P consists of a set of distinct positive integers. The sequence C contains all the terms of arithmetic sequences N and P such that the number of terms in sequence C is equal to the number of terms in arithmetic sequences N and P. Is sequence C an arithmetic sequence?(1) The sum of the largest term of the sequence N and the smallest term of the sequence P is zero.(2) For every integer in sequence N, there exists an integer in sequence P with the same magnitude.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
An arithmetic sequence is a sequence in which each term after the first is equal to the sum of the preceding term and a constant, which is also known as the common difference of that arithmetic sequence. An increasing arithmetic sequence N consists of a set of distinct negative integers and an increasing arithmetic sequence P consists of a set of distinct positive integers. The sequence C contains all the terms of arithmetic sequences N and P such that the number of terms in sequence C is equal to the number of terms in arithmetic sequences N and P. Is sequence C an arithmetic sequence?
(1) The sum of the largest term of the sequence N and the smallest term of the sequence P is zero.
(2) For every integer in sequence N, there exists an integer in sequence P with the same magnitude.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Moumita Sen answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Increasing arithmetic sequence N consist of distinct negative integers with common difference n
- Increasing arithmetic sequence P consist of distinct positive integers with common difference m.
- Sequence C consist of terms of sequences N and P only.
To Find: Is sequence C an arithmetic sequence?
- As sequence C consists of terms of arithmetic sequences N and P only, for sequence C to be arithmetic, sequences N and P should have the same common difference.
- Also, sequences N and P will not have any common terms (as sequence N has all negative integers and sequence P has only positive integers), for sequence C to be arithmetic, the difference between the largest term of sequence N and the smallest term of sequence P should be equal to the common difference of the sequences.
- For ex: Consider N = { -10, -9, -8……-1) and P = { 2, 3, 4, 5, ….}. In this case, both the sequences N and P have the same common difference but combining their terms does not result in an arithmetic sequence because the difference between -1 and 2 is not equal to the common difference of the sequences.
- Consider N = { -14, -10, -6, -2} and P = {2, 6, 10}. In this case, as the difference between -2 and 2 is equal to the common differences of the sequences(i.e. 4), combining the terms of both the sequences results in an arithemetic sequence.
Step 3: Analyze Statement 1 independently
(1) The sum of the largest term of the sequence N and the smallest term of the sequence P is zero.
- Let the largest term of sequence N be x and the smallest term of the sequence P be y.
- So, x + y = 0
- x = -y
- So, difference between y and x = y – x = 2y
However we do not know the value of the common differences of the sequences as well as we do not know the value of y.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) For every integer in sequence N, there exists an integer in sequence P with the same magnitude.
- It tells us that integers in sequence P consist of negative of all the integers in sequence N. Following cases are possible:
- Number of terms of sequence N and P are the same. For ex: N= {-8, -6, -4} and P = {4, 6, 8}. In this case the common difference of both the sequences will be equal.
- Number of terms in sequence P is greater than the number of terms in sequence N. For ex: N = {-8, -6, -4} and P = {3, 4, 5, 6, 7, 8, 9} or { 4, 6, 8, 10, 12}. In this case the common difference may or may not be equal.
Also, as we do not know the difference between the largest term of sequence N and the smallest term of sequence P, the statement is insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
- Difference between the largest term of sequence N( i.e. x) and the smallest term of sequence P(i.e. y) is equal to 2y.
- For every integer in sequence N, there exists an integer in sequence P with the same magnitude
Combining both the statements tell us that the largest term of sequence N (i.e. x) and the smallest term of sequence P(i.e. y ) have the same magnitude.
However it does not tell us:
- the value of y and
- if the sequences have the same common difference
Hence, combining the statements is also insufficient to answer.
Answer: E
Steven and Stuart took a job in different companies at the same time. Steven’s salary increased by a fixed amount at the end of every year and Stuart’s salary increased by a fixed percentage at the end of every year. If the increase in the salary of Steven at the end of the third year was equal to the increase in the salary of Stuart at the end of the second year, what was the difference in the salaries of Steven and Stuart when they took the job?(1) Steven’s salary after 2 years was 20% more than the salary at which he took the job(2) The increase in the salary of Stuart at the end of the second year was 11% of the salary at which he took the job.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
Steven and Stuart took a job in different companies at the same time. Steven’s salary increased by a fixed amount at the end of every year and Stuart’s salary increased by a fixed percentage at the end of every year. If the increase in the salary of Steven at the end of the third year was equal to the increase in the salary of Stuart at the end of the second year, what was the difference in the salaries of Steven and Stuart when they took the job?
(1) Steven’s salary after 2 years was 20% more than the salary at which he took the job
(2) The increase in the salary of Stuart at the end of the second year was 11% of the salary at which he took the job.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Kavya Chakraborty answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Let Steven’s initial salary be S1
and Stuart’s initial salary be S1
- Let Steven’s salary increase by x every year and Steven’s salary increase by y% every year.
- Steven’s salary increase in the 3rd year = x
- Stuart’s salary increase at the end of the 2nd year = y% of (Stuart’s salary in the 2nd year)
- Steven’s salary increase in the 3rd year = Stuart’s salary increase in the 2nd year
To Find: S1−S2
Step 3: Analyze Statement 1 independently
(1) Steven’s salary after 2 years was 20% more than the salary at which he took the job
- Steven’s salary after 2 years =S1+2x
However, we do not know anything about the values of S2, x and y.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The increase in the salary of Stuart at the end of the second year was 11% of the salary at which he took the job.
- Increase in Stuart’s salary at the end of the 2nd year =
Insufficient to answer as it does give us the value of S1,S2orx
Step 5: Analyze Both Statements Together (if needed)
Need to know the value of x to answer the question.
Insufficient to answer.
Answer: E
For any positive integer z, SZ denotes the sum of the first z positive integers. For example S3 = 1+2 + 3 = 6. Which of the following expressions is correct?
- a)I only
- b)II only
- c)III only
- d)I and II only
- e)II and III only
Correct answer is option 'E'. Can you explain this answer?
For any positive integer z, SZ denotes the sum of the first z positive integers. For example S3 = 1+2 + 3 = 6. Which of the following expressions is correct?
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
II and III only

|
Gitanjali Kumar answered |
Given:
- For a positive integer z, Sz = 1 + 2 + 3 + . . . + z
To find: Which of the given 3 expressions is correct?
Approach:
- Since the 3 expressions are independent of one another (that is, they do not talk about the same value or item), we will evaluate the expressions one by one, using the given definition of SZ
Working Out:
- Now, by definition, S25 is the sum of the first 25 integers.
By definition,
- So, 2S10 + 15 = 2*55 + 15
- This value is clearly much smaller in magnitude than 25*13
- Therefore, Expression 1 is not true.
- Evaluating Expression II

- Thus, we see that S50 is indeed equal to 2S25 + 625
- Therefore, Expression II is correct
- Evaluating Expression III
- S99 = 2S50 + 2400
- Note: You can calculate Expression III using the formula for the sum of an arithmetic sequence. The working out for this method will be similar to the working out shown above for Expressions I and II. Alternatively, you can solve as below. This is an alternate way of evaluating the given expressions. This way can also be used to evaluate Expressions I and II.
- S99 = 1 + 2 + 3 + . . . . + 99
- = (1 + 2 + 3 + . . . + 99 + 100) – 100
- = (1 + 2 + 3 + . . . + 50) + (51 + 52 + . . . + 100) - 100
- = S50 + {(50+1) + (50 + 2) . . . + (50 + 50)} – 100
- = S50 + 50*50 + (1 + 2 + 3 + . . . + 50) – 100
- = S50 + 2400 + S50
- = 2S50 + 2400
- Thus, Expression III is indeed correct
- Conclusion
- So, we have determined that of the 3 given expressions, only Expressions II and III are correct.
Looking at the answer choices, we see that the correct answer is Option E
An arithmetic sequence is a sequence in which each term after the first is equal to the sum of the preceding term and a constant, which is also known as the common difference of that arithmetic sequence. The sequence S contains all the terms of two different increasing arithmetic sequences P and Q such that the number of terms in sequence S is equal to the sum of the number of terms in sequences P and Q. If each of the arithmetic sequences P and Q consists of 10 positive integral terms, how many distinct terms does sequence S have?(1) The least common multiple of the common differences of the sequences P and Q is 6(2) The third term of the sequence P is equal to the second term of the sequence Q- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
An arithmetic sequence is a sequence in which each term after the first is equal to the sum of the preceding term and a constant, which is also known as the common difference of that arithmetic sequence. The sequence S contains all the terms of two different increasing arithmetic sequences P and Q such that the number of terms in sequence S is equal to the sum of the number of terms in sequences P and Q. If each of the arithmetic sequences P and Q consists of 10 positive integral terms, how many distinct terms does sequence S have?
(1) The least common multiple of the common differences of the sequences P and Q is 6
(2) The third term of the sequence P is equal to the second term of the sequence Q
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Kavya Chakraborty answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Increasing arithmetic sequence P with 10 positive integral terms with a common difference of p
- Increasing arithmetic sequence Q with 10 positive integral terms with a common difference of q.
- Sequence S consists of all the terms of sequences P and Q only, i.e. it consists of 20 terms only
To Find: Number of distinct terms of sequence S
- Number of distinct terms in sequence S = 20 – number of terms that are common to sequences P and Q ( as sequence S consists of terms from sequences P and Q only)
- To find the number of terms that are common to sequences P and Q, we need to find:
- The smallest term that is common to both the sequences
- The common difference of both the sequences i.e. values of p and q.
Step 3: Analyze Statement 1 independently
(1) The least common multiple of the common differences of the sequences P and Q is 6
- We are given the LCM of the common differences of the sequences P and Q is 6.
- 6 = 2 * 3.
- Hence the common differences (p, q) can be (1, 6) , (2, 6), (3, 6), (6, 6) or (2, 3) in any order
- So, we not have the unique values of the common difference of the two sequences
- Also, we do not know the smallest term, which is common to both the sequences.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The third term of the sequence P is equal to the second term of the sequence Q
- We are given that P3 = Q2
- We do not know if these are the smallest terms of the sequences P and Q that are common.Let us assume that these are not the smallest terms that are common to sequences P and Q. So, the possible cases can be:
- All the three cases are possible(i.e. Q1 and P1, or Q1 and P2 or Q2 and P3 are the smallest terms of the sequences that are common). So we cannot identify the smallest terms of the sequences P and Q that are common.
Also, we do not know the common difference of the two sequences. Hence the statement is insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
- Common differences of sequences P and Q = (1, 6) , (2, 6), (3, 6), (6, 6) or (2, 3) in any order
- P3 = Q2
Uisng (1) and (2), we cannot calculate the unique common values of the common differences as well as we do not know if P3 and Q2 are the smallest terms of the sequences P and Q that are common.
Hence, insufficient to answer.
Answer: E
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -Q. Is x/y a terminating decimal?1. x is a multiple of 2
2. y is a multiple of 3- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. Is x/y a terminating decimal?
1. x is a multiple of 2
2. y is a multiple of 3
2. y is a multiple of 3
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Nikhil Khanna answered |
Step 1 of solving this GMAT DS question: Understand the Question Stem
What kind of an answer will the question fetch?
The question is an "Is" question. Answer to an "is" question is either YES or NO.
What kind of an answer will the question fetch?
The question is an "Is" question. Answer to an "is" question is either YES or NO.
When is the data sufficient?
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
If the statements do not have adequate data to provide a CONCLUSIVE answer and we get YES for some instances and NO for others, the given data is NOT sufficient.
What is a terminating decimal?
Numbers that have finite number of digits after the decimal point are called terminating or finite decimals. e.g., 2.5, 0.25, 8.
Note: All integers are terminating decimals.
Numbers that have finite number of digits after the decimal point are called terminating or finite decimals. e.g., 2.5, 0.25, 8.
Note: All integers are terminating decimals.
Numbers that have infinite digits after the decimal point are called non-terminating or infinite decimals
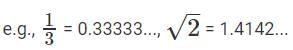
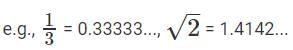
Step 2 of solving this GMAT DS question: Evaluate Statement (1) ALONE
Statement (1) : x is a multiple of 2
Statement (1) : x is a multiple of 2
No information about y has been provided.
Approach: Let us look for a counter example.
Approach: Let us look for a counter example.
Example: When x = 2 and y = 3, x/y is non-terminating.
The answer to the question is NO.
The answer to the question is NO.
Counter Example: When x = 2 and y = 4, x/y is terminating.
The answer to the question is YES.
The answer to the question is YES.
We have found a counter example. Therefore, statement 1 does not provide a DEFINITE answer.
Statement 1 ALONE is NOT sufficient.
Eliminate choices A and D. Choices narrow down to B, C or E.
Eliminate choices A and D. Choices narrow down to B, C or E.
Step 3 of solving this GMAT DS question: Evaluate Statement (2) ALONE
Statement (2) : y is a multiple of 3
Statement (2) : y is a multiple of 3
No information about x has been provided.
Approach: Let us look for a counter example.
Approach: Let us look for a counter example.
Example:When x = 3 and y = 3, xyxy is terminating.
The answer to the question is YES.
The answer to the question is YES.
Counter Example: When x = 2 and y = 3, x/y is non-terminating.
The answer to the question is NO.
The answer to the question is NO.
We have found a counter example. Therefore, statement 2 does not provide a DEFINITE answer.
Statement 2 ALONE is NOT sufficient.
Eliminate choice B. Choices narrow down to C or E.
Statement 2 ALONE is NOT sufficient.
Eliminate choice B. Choices narrow down to C or E.
Step 4 of solving this GMAT DS question Evaluate Statements (1) & (2) Together
Statements Together : x is a multiple of 2 & y is a multiple of 3
Statements Together : x is a multiple of 2 & y is a multiple of 3
Approach: Let us look for a counter example.
Example:When x = 6 and y = 6, x/y is terminating.
The answer to the question is YES.
The answer to the question is YES.
Counter Example: When x = 2 and y = 3, x/y is non-terminating.
The answer to the question is NO.
The answer to the question is NO.
We have found a counter example. Despite combining the information in the statements we are not able to find a DEFINITE answer.
Statements TOGETHER are NOT SUFFICIENT. Choice E is the answer.
A sequence S consists of 5 distinct positive integers. Are all the integers in the sequence divisible by 5?(1) The sum of all the integers in the sequence is divisible by 5.(2) The product of all the integers in the sequence is divisible by 5 but not by 10.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
A sequence S consists of 5 distinct positive integers. Are all the integers in the sequence divisible by 5?
(1) The sum of all the integers in the sequence is divisible by 5.
(2) The product of all the integers in the sequence is divisible by 5 but not by 10.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Kirti Roy answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Sequence S consists of a1,a2,a3,a4,a5
- , where all the terms are integers > 0
To Find: Is a1,a2,a3,a4,a5 divisible by 5?
Step 3: Analyze Statement 1 independently
(1) The sum of all the integers in the sequence is divisible by 5.
a1+a2+a3+a4+a5=5x
, where x is an integer > 0.
Two cases arise:
- All of a1,a2,a3,a4,a5 are a multiple of 5. In this case all the terms are divisible by 5
- Two or more terms sum up to a multiple of 5. In this case all the terms are not divisible by 5.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The product of all the integers in the sequence is divisible by 5 but not by 10.
a1∗a2∗a3∗a4∗a5=5y, where y is an integer > 0
For the product of the terms to be divisible by 5, any one or more of the terms should be divisible by 5.
So, 1 or all the 5 terms may be divisible by 5.
Also, as the product of the terms is not divisible by 10, none of the terms is even.
Insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
(1) a1+a2+a3+a4+a5=5x
(2) a1∗a2∗a3∗a4∗a5=5y and none of a1,a2,a3,a4,a5 is even
Following cases may arise:
- All the terms are odd multiples of 5.
- 1 or more terms are an odd multiple of 5 and the rest terms are odd and not a multiple of 5 but sum up to be a multiple of 5.
Insufficient to answer.
Answer: E
A certain club has exactly 5 new members at the end of its first week. Every subsequent week, each
of the previous week's new members (and only these members) brings exactly x new members into the club. If y is the number of new members brought into the club during the twelfth week, which of the following could be y?- a)
- b)311511
- c)312512
- d)311512
- e)6012
Correct answer is option 'D'. Can you explain this answer?
A certain club has exactly 5 new members at the end of its first week. Every subsequent week, each
of the previous week's new members (and only these members) brings exactly x new members into the club. If y is the number of new members brought into the club during the twelfth week, which of the following could be y?
of the previous week's new members (and only these members) brings exactly x new members into the club. If y is the number of new members brought into the club during the twelfth week, which of the following could be y?
a)
b)
311511
c)
312512
d)
311512
e)
6012

|
Ruchi Pillai answered |
At the end of the first week, there are 5 members. During the second week, 5x new members are brought in (x new members for every existing member). During the third week, the previous week's new members (5x) each bring in x new members:
(5x)x= 5x2 new members. If we continue this pattern to the twelfth week, we will see that 5x11 new members join the club that week. Since y is the number of new members joining during week 12, y=5x11.
if y=5x11, we can set each of the answer choices equal to 5x11 and see which one yields an integer value (since y is a specific number of people, it must be an integer value). The only choice to yield an integer value is (D)
5x11= 311512
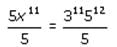
x11 = 311512
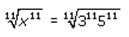
x=(3)(5)
Therefore x = 15.
Since choice (D) is the only one to yield an integer value, it is the correct answer.
(5x)x= 5x2 new members. If we continue this pattern to the twelfth week, we will see that 5x11 new members join the club that week. Since y is the number of new members joining during week 12, y=5x11.
if y=5x11, we can set each of the answer choices equal to 5x11 and see which one yields an integer value (since y is a specific number of people, it must be an integer value). The only choice to yield an integer value is (D)
5x11= 311512
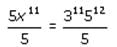
x11 = 311512
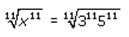
x=(3)(5)
Therefore x = 15.
Since choice (D) is the only one to yield an integer value, it is the correct answer.
An increasing sequence M consists of 5 consecutive positive multiples of a positive integer. What is the remainder when the largest term of the sequence is divided by 2?(1) The median of the sequence is even.(2) The second term of the sequence is odd.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
An increasing sequence M consists of 5 consecutive positive multiples of a positive integer. What is the remainder when the largest term of the sequence is divided by 2?
(1) The median of the sequence is even.
(2) The second term of the sequence is odd.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Kavya Chakraborty answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Let the positive integer of which the multiples are present in sequence M be p
- Let the terms of the sequence be {p*d, p*(d+1)……….p*(d+4)}
To Find:
- Remainder when the largest term of the sequence is divided by 2
- That is remainder when p*(d+4) is divided by 2
- Any positive integer divided by 2 leaves a remainder 0 or 1
- If p * (d +4) is even, then remainder will be 0
- If p* (d +4) is odd, then remainder will be 1
- r = { 0 or 1}.
- So we need to determine if p*(d+4) is even or odd.
- p*(d+4) will be odd, if both the terms 'p' and 'd' are odd.
- p*(d+4) will be even, if atleast one of the term is even.
Step 3: Analyze Statement 1 independently
(1) The median of the sequence is even.
- The median of sequence = p*(d+2) is even. Following cases are possible:
- Only p is even. In this case, p*d(+4) will be even.
- Only (d+2) is even. In this case, d+4 will be even, hence p*(d+4) will be even
- Both p and (d+2) are even. In this case, p*(d+4) are even.
Alternate method
- If p*(d+2) is even, we can write
- p*(d+4) = p*(d+2+2) = p*(d+2) + 2p = even + even = even
- Thus, p*(d+4) will always be even.
Sufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The second term of the sequence is odd.
- p*(d+1) is odd, which is possible only if:
- p and (d+1) both are odd.
- If (d+1) is odd, (d+4) will be even. Hence p*(d+4) will be even.
- p and (d+1) both are odd.
Sufficient to answer
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from steps 3 and 4, this step is not required.
Answer: D
The sequence S consists of 10 terms: x, x2, x3……x10, where x is a non-zero number. If P is the sum of all the terms in the sequence S, is P3> 0?(1) The distance of any term of the sequence S from zero on the number line is not less than 1.(2) x5 = x7- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
The sequence S consists of 10 terms: x, x2, x3……x10, where x is a non-zero number. If P is the sum of all the terms in the sequence S, is P3
> 0?
(1) The distance of any term of the sequence S from zero on the number line is not less than 1.
(2) x5 = x7
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Manasa Kulkarni answered |
Steps 1 & 2: Understand Question and Draw Inferences
- Sequence S= {x,x2,x3,…….x10}
- P = x+x2+x3+…….+x10
To Find: Is P3> 0 ?
- P3 > 0. If P > 0 (Since P is raised to an odd power that does not affects its sign)
- As P = x+x2+x3……….+x10 , the positive or negative nature of P will depend on the positive or negative nature of x. Hence, following cases can arise:
- If x > 0 → In this case, x,x2,x3,…….x10 > 0. So, their sum will also be positive. Hence P > 0
- If x < 0 → The terms with an odd power i.e. x,x2,x3,…….x9< 0 and the terms with an even power i.e. x,x2,x3,…….x10 > 0. So, the value of P will depend on the sum of the terms with an odd power and the terms with an even power. Also we know that if -1 < x < 0, with increasing power the magnitude of the terms decrease ( |x| > |x2|, while if x < -1, the magnitude of the terms increase with increasing power(|x| < |x2|). So, the following cases are possible:
- To understand the nature of P, let’s evaluate the first term of P in the equation above i.e.x + x2. Here x < 0 and x2 > 0. Since the magnitude of x is less than 1, the magnitude of x2 will be less than x. For ex: if x = -0.5, x2 = 0.25. Hence x + x2 < 0. Similarly x3 + x4 < 0. So, we see here that P is the sum of 5 negative numbers. Hence P < 0.
- To understand the nature of P, let’s evaluate the first term of P in the equation above i.e. x + x2. Here x < -1 and x2 > 0. Since the magnitude of x is greater than 1, the magnitude of x2 will be greater than x. For ex: if x = -2, x2 = 4. Hence x + x2 > 0. Similarly x3 + x4 > 0. So, we see here that P is the sum of 5 positive numbers. Hence P > 0.
- However there may be a case where the terms
- This would be possible when x(x+1) = 0, i.e. x = 0 or -1. As x≠ 0, for x = -1, P = 0.
So, P > 0, except when -1 < x < 0. Hence, we need to find if -1 < x < 0.
Step 3: Analyze Statement 1 independently
(1) The distance of any term of the sequence S from zero on the number line is not less than 1.
- As the distance of all the terms of the sequence from zero is not less than 1, the distance of the first term i.e. |x| ≥ 1. If |x| ≥ 1, ∣∣x2∣∣≥1………………….∣∣x10∣∣≥1
- So, x ≥ 1 or x ≤ -1. Following cases can arise:
So, we cannot say for sure if P > 0 or not. Insufficient to answer.
Step 4: Analyze Statement 2 independently
- If x = -1, P = 0
- x ≠ 0(given in the question statement)
- If x = 1, P > 0
So, we cannot say for sure if P > 0. Insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
- x ≥ 1 or ≤ -1
- x = -1 or 1
Combining both the statements, we have x = -1 or 1.
- If x = -1, P = 0
- If x = 1, P > 0
So, we cannot say for sure if P > 0.
Insufficient to answer.
Answer: E
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -Q. Is xy < 0?1. 5|x| + |y| = 0
2. |x| + 5|y| = 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question aske
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. Is xy < 0?
1. 5|x| + |y| = 0
2. |x| + 5|y| = 0
2. |x| + 5|y| = 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question aske
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Saumya Shah answered |
Step 1 of solving this GMAT DS question: Understand the Question Stem
What kind of an answer will the question fetch?
The question is an "Is" question. Answer to an "is" question is either YES or NO.
The question is an "Is" question. Answer to an "is" question is either YES or NO.
When is the data sufficient?
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
If the answer is MAYBE or DONOT KNOW, the data is NOT sufficient.
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
If the answer is MAYBE or DONOT KNOW, the data is NOT sufficient.
When is the answer YES and when is it NO?
If xy < 0, the answer is YES. If xy ≥ 0, the answer is NO.
Note: If xy = 0, the answer is NO.
If xy < 0, the answer is YES. If xy ≥ 0, the answer is NO.
Note: If xy = 0, the answer is NO.
Step 2 of solving this GMAT DS question :
Evaluate Statement (1) ALONE: 5|x| + |y| = 0
Evaluate Statement (1) ALONE: 5|x| + |y| = 0
Modulus of any real number will always be non-negative.
So, if 5|x| + |y| = 0, then the only possibility is that x = 0 and y = 0.
Therefore, xy = 0.
Or xy is not negative.
The answer is a DEFINITE NO.
So, if 5|x| + |y| = 0, then the only possibility is that x = 0 and y = 0.
Therefore, xy = 0.
Or xy is not negative.
The answer is a DEFINITE NO.
Statement 1 ALONE is sufficient.
Eliminate choices B, C and E. Choices narrow down to A or D.
Eliminate choices B, C and E. Choices narrow down to A or D.
Step 3 of solving this GMAT DS question :
Evaluate Statement (2) ALONE: |x| + 5|y| = 0
Evaluate Statement (2) ALONE: |x| + 5|y| = 0
Modulus of any real number will always be non-negative.
So, if |x| + 5|y| = 0, then the only possibility is that x = 0 and y = 0.
Therefore, xy = 0.
Or xy is not negative.
The answer is a DEFINITE NO.
So, if |x| + 5|y| = 0, then the only possibility is that x = 0 and y = 0.
Therefore, xy = 0.
Or xy is not negative.
The answer is a DEFINITE NO.
Statement 2 ALONE is also sufficient.
Eliminate choice A.
Eliminate choice A.
Each statement is INDEPENDENTLY sufficient. Choice D is the answer.
A list contains distinct integers a1, a2, …a10 arranged in ascending order. If the integers of the list lie between -19 and 19, inclusive such that the distance between any two consecutive integers is equal, is one of the terms of this list equal to zero?(1) All the integers in the list are divisible by 2(2) a4 = -6- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
A list contains distinct integers a1, a2, …a10 arranged in ascending order. If the integers of the list lie between -19 and 19, inclusive such that the distance between any two consecutive integers is equal, is one of the terms of this list equal to zero?
(1) All the integers in the list are divisible by 2
(2) a4 = -6
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Rhea Gupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
- a1, a2, …a10 is an arithmetic sequence
- Maximum Range of the sequence = 19 –(-19)= 38
- If a1 = -19, the maximum value of common difference can be for a value where a10 ≤ 19
- a1+ 9d ≤ 19, d ≤ 4.2
- Possible values of d = {1, 2, 3, 4}
Step 3: Analyze Statement 1 independently
(1) All the integers in the list are divisible by 2
- As all the terms of the sequence are even, the difference between any two consecutive terms should also be even.
- So, possible values of d can be {2 or 4}
- d =2, the range of the sequence will be 9d = 18. Let’s try to see if we can form a sequence that contains all the positive or negative terms
- If a1 = -18, a10 = a1 +9d= -18 +9*2 = 0
- If a10 = 18, a1 = a10 – 9d = 18 – 9*2 = 0
- For all the other sequences consisting of both positive and negative terms, 0 will be a part of the sequence
- d =2, the range of the sequence will be 9d = 18. Let’s try to see if we can form a sequence that contains all the positive or negative terms
- d= 4, the range of the sequence will be 9d = 36
- If a1 = -18, a10 = a1 +9d = -18 +36 = 18. The terms of the sequence = {-18,-14,-10,-6,-2,2…18}. Hence, 0 is not a part of the sequence.
- There is no other sequence possible with d = 4
As we do not have a unique answer, the statement is insufficient to answer the question
Step 4: Analyze Statement 2 independently
(2) a4 = -6
- Difference between -6 and 0 = 6
- 0 will be a part of the sequence if d = {1,2 or 3}
- If d= 4, 0 will not be a part of the sequence
Hence, cannot say for sure if 0 is a part of the sequence. Insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
(1) d = {2, 4}
(2) a4 = -6
- If d = 2, 0 will be a part of the sequence
- If d= 4, 0 will not be a part of the sequence.
Insufficient to answer
Answer: E
An increasing sequence P consists of 10 distinct integers. How many integers of the sequence are less than 16?(1) The difference between any two integers of the sequence is divisible by 2 and 3.(2) If the third term of the sequence P is removed, the magnitude of the product of the terms of the sequence remains unchanged.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
An increasing sequence P consists of 10 distinct integers. How many integers of the sequence are less than 16?
(1) The difference between any two integers of the sequence is divisible by 2 and 3.
(2) If the third term of the sequence P is removed, the magnitude of the product of the terms of the sequence remains unchanged.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Sharmila Singh answered |
Steps 1 & 2: Understand Question and Draw Inferences
Step 3: Analyze Statement 1 independently
(1) The difference between any two integers of the sequence is divisible by 2 and 3.
- Tells us that the difference between any two integers is of the form (2*3)k = 6k, where k is an integer > 0.
Does not tell us anything about the values of the integers of sequence P.
Insufficient to answer.
Step 4: Analyze Statement 2 independently
(2) If the third term of the sequence P is removed, the magnitude of the product of the terms of the sequence remains unchanged.
- So, the third term i.e. a3 = 1 or -1
The statement does not tell us anything about the other terms.
Insufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
(1) Difference between any two integers is of the form (2*3)k = 6k
(2) a3 = 1 or -1
Combining both the statements, we cannot say for sure how many terms are less than 16, as we do know the value of 6k.
So, 6k = 6, 12 or 18.
For each case, we will have a different answer.
Insufficient to answer
Answer: E
A city had 1000 migrants in the year 1999. If the number of migrants in the city has doubled every 3 years since 1999, then what was the increase in the population of migrants during the period from 2008 to 2011?- a)2000
- b)4000
- c)8000
- d)16000
- e)32000
Correct answer is option 'C'. Can you explain this answer?
A city had 1000 migrants in the year 1999. If the number of migrants in the city has doubled every 3 years since 1999, then what was the increase in the population of migrants during the period from 2008 to 2011?
a)
2000
b)
4000
c)
8000
d)
16000
e)
32000

|
Jatin Kapoor answered |
Given
- Number of migrants in the year 1999 = 1000
- Number of migrants doubles every 3 years
To Find:
- Increase in migrants population from 2008 to 2011?
- Migrants Population in 2011 – Migrants Population in 2008
Approach
- As we know that the migrants population doubles every 3 years and migrants population in 1999 = 1000, we can use this information to calculate the migrants population in the year 2008 and the year 2011.
Working Out
- Migrants population in year 1999 = 1000
- Migrants population after (2008 – 1999 = 9 years) i.e. 3 intervals of 3 years = 1000 * 23
- Migrants population after (2011 – 1999 = 12 years) i.e. after 4 intervals of 3 years= 1000 * 24
- Difference in migrants population = 1000 *(24−23)=1000∗8=8000
Hence, the migrants population increased by 8000 between 2008 and 2011.
Answer: C
Sn = 2Sn-1 + 4 and Qn = 4Qn-1 + 8 for all n > 1. If S5 = Q4 and S7 = 316, what is the first value of n for whichQn is an integer?- a)1
- b)2
- c)3
- d)4
- e)5
Correct answer is option 'C'. Can you explain this answer?
Sn = 2Sn-1 + 4 and Qn = 4Qn-1 + 8 for all n > 1. If S5 = Q4 and S7 = 316, what is the first value of n for whichQn is an integer?
a)
1
b)
2
c)
3
d)
4
e)
5

|
Gauri Iyer answered |
If S7 = 316, then 316 = 2S6 + 4, which means that S6=156.
We can then solve for S5:
156 = 2S5 + 4, so S5 = 76
Since S5 = Q4, we know that Q4 = 76 and we can now solve for previous Qn’s to find the first n value for which Qn is an integer.
To find Q3: 76 = 4Q3 + 8, so Q3 = 17
To find Q2: 17 = 4Q2 + 8, so Q2 = 9/2
It is clear that Q1 will also not be an integer so there is no need to continue.
Q3 (n = 3) is the first integer value.
We can then solve for S5:
156 = 2S5 + 4, so S5 = 76
Since S5 = Q4, we know that Q4 = 76 and we can now solve for previous Qn’s to find the first n value for which Qn is an integer.
To find Q3: 76 = 4Q3 + 8, so Q3 = 17
To find Q2: 17 = 4Q2 + 8, so Q2 = 9/2
It is clear that Q1 will also not be an integer so there is no need to continue.
Q3 (n = 3) is the first integer value.
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -Q. Is the positive integer X divisible by 21?1. When X is divided by 14, the remainder is 4
2. When X is divided by 15, the remainder is 5- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. Is the positive integer X divisible by 21?
1. When X is divided by 14, the remainder is 4
2. When X is divided by 15, the remainder is 5
2. When X is divided by 15, the remainder is 5
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Mihir Nambiar answered |
Step 1 of solving this GMAT DS question: Understand the Question Stem
What kind of an answer will the question fetch?
The question is an "Is" question. Answer to an "is" question is either YES or NO.
The question is an "Is" question. Answer to an "is" question is either YES or NO.
When is the data sufficient?
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
If we get a MAYBE as an answer, the data is NOT sufficient
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
If we get a MAYBE as an answer, the data is NOT sufficient
Do we have any more information about 'X' from the question stem?
The question stem states that 'X' is a positive integer.
The question stem states that 'X' is a positive integer.
What kind of numbers will be divisible by 21?
A number is divisible by 21 if it is divisible by 3 and 7.
A number is divisible by 21 if it is divisible by 3 and 7.
Step 2 of solving this GMAT DS question Evaluating Statement (1) ALONE
Statement (1) : When X is divided by 14, the remainder is 4
Statement (1) : When X is divided by 14, the remainder is 4
The number is, therefore, of the form 14k + 4.
It will leave a remainder of 4 when divided by 7. (14k is divisible by 7. When 4 is divided by 7, the remainder is 4.)
It will leave a remainder of 4 when divided by 7. (14k is divisible by 7. When 4 is divided by 7, the remainder is 4.)
This number is definitely not divisible by 7.
To be divisible by 21, the number must be divisible by both 3 and 7. This number is not divisible by 7. Hence, X is not divisible by 21.
To be divisible by 21, the number must be divisible by both 3 and 7. This number is not divisible by 7. Hence, X is not divisible by 21.
We have a DEFINITE NO as the answer to the question using statement 1.
Statement 1 ALONE is sufficient.
Eliminate choices B, C and E. Choices narrow down to A or D.
Eliminate choices B, C and E. Choices narrow down to A or D.
Step 3 of solving this GMAT DS question Evaluating Statement (2) ALONE
Statement (2) : When X is divided by 15, the remainder is 5
Statement (2) : When X is divided by 15, the remainder is 5
The number X is of the form 15m + 5
Therefore, the number will leave a remainder of 2 when divided by 3.
Therefore, the number will leave a remainder of 2 when divided by 3.
Hence, it is not divisible by 3.
To be divisible by 21, the number must be divisible by both 3 and 7. This number is not divisible by 3. Hence, X is not divisible by 21.
To be divisible by 21, the number must be divisible by both 3 and 7. This number is not divisible by 3. Hence, X is not divisible by 21.
We have a DEFINITE NO as the answer to the question using statement 2 as well.
Statement 2 ALONE is also sufficient.
Eliminate choice A.
Eliminate choice A.
240 students are to be arranged in n rows in the assembly hall of a school. If the first row is the closest to the stage and each subsequent row has 10 more students than the row ahead of it, what is the value of n?(1) There are 45 students in the 4th row from the stage.(2) The number of students in the nth row is 10 less than 5 times the number of students in the first row.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
240 students are to be arranged in n rows in the assembly hall of a school. If the first row is the closest to the stage and each subsequent row has 10 more students than the row ahead of it, what is the value of n?
(1) There are 45 students in the 4th row from the stage.
(2) The number of students in the nth row is 10 less than 5 times the number of students in the first row.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Rhea Gupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
- As the number of students in a row is 10 more than the number of students in the previous row, the number of students in the rows form an arithmetic sequence with common difference, d = 10
- Number of rows = n
- Let the number of students in the first row be a1
and that in the last row be an
To Find: Unique value of n
- Need to find the value of a1 or express a1 in terms of n to find the value of n.
Step 3: Analyze Statement 1 independently
(1) There are 45 students in the 4th row from the stage.
Substituting the value of a1 in (1), we have
As n cannot be negative, n = 6.
Sufficient to answer.
Step 4: Analyze Statement 2 independently
(2) The number of students in the nth row is 10 less than 5 times the number of students in the first row.
Putting the value of in (1), we have
As n has to be an integer, n = 6.
Sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from steps 3 and 4, this step is not required.
Answer: D
In the sequence S, the difference between any two consecutive terms is equal. If the sum of the fourth term and the fifth term of the sequence is equal to the seventh term of the sequence, what is the value of the second term of the sequence?- a)-4
- b)0
- c)4
- d)8
- e)Can't be determined
Correct answer is option 'B'. Can you explain this answer?
In the sequence S, the difference between any two consecutive terms is equal. If the sum of the fourth term and the fifth term of the sequence is equal to the seventh term of the sequence, what is the value of the second term of the sequence?
a)
-4
b)
0
c)
4
d)
8
e)
Can't be determined

|
Sharmila Singh answered |
Given
- In a sequence S, difference between any two terms is equal
- S is an arithmetic sequence
- Let the first term of the sequence be a and the common difference be d
- 4th term + 5th term = 7th term
- 4th term = a + (4-1)*d = a+ 3d
- 5th term = a + (5-1)*d = a +4d
- 7th term = a + (7-1)d = a + 6d
To Find: a + d = ?
Approach
- To find the value of a + d, we need to either find the values of a and d or a + d
- We are given a relation
- (a + 3d) + (a + 4d) = a + 6d
- As we are given only one equation between a and d, we will be unable to find the values of both a and b. So, we will try to see if we can find the value of a + d
Working Out
- (a + 3d) + (a+4d) = a+ 6d
- 2a + 7d = a + 6d
- a + d = 0
Hence, the value of the 2nd term of the sequence = a + d = 0
Answer: B
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -Q. If x and y are positive integers, is y odd?1. x is odd.
2. xy is odd.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'B'. Can you explain this answer?
This data sufficiency problem consists of a question and two statements, labeled (1) and (2), in which certain data are given. You have to decide whether the data given in the statements are sufficient for answering the question. Using the data given in the statements, plus your knowledge of mathematics and everyday facts (such as the number of days in a leap year or the meaning of the word counterclockwise), you must indicate whether -
Q. If x and y are positive integers, is y odd?
1. x is odd.
2. xy is odd.
2. xy is odd.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Devansh Shah answered |
Step 1 of solving this GMAT DS question: Understand the Question Stem
What kind of an answer will the question fetch?
The question is an "Is" question. Answer to an "is" question is either YES or NO.
The question is an "Is" question. Answer to an "is" question is either YES or NO.
When is the data sufficient?
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
If the answer is MAYBE or DONOT KNOW, the data is NOT sufficient.
The data is sufficient if we are able to get a DEFINITE YES or a DEFINITE NO from the information given in the statements.
If the answer is MAYBE or DONOT KNOW, the data is NOT sufficient.
Do we have any more information about x and y from the question stem?
The question stem states that both x and y are positive integers.
The question stem states that both x and y are positive integers.
Step 2 of solving this GMAT DS question: Evaluate Statement (1) ALONE
Statement (1) : x is odd.
Statement (1) : x is odd.
The statement provides no information about y.
Statement 1 ALONE is NOT sufficient.
Eliminate choices A and D. Choices narrow down to B, C or E.
Eliminate choices A and D. Choices narrow down to B, C or E.
Step 3 of solving this GMAT DS question: Evaluate Statement (2) ALONE
Statement (2) : xy is odd.
Statement (2) : xy is odd.
Given that x and y are integers and that the product xy is odd, both x and y have to be odd (product of two odd integers is odd).
We can answer the question with a definite YES.
We can answer the question with a definite YES.
Eliminate choices C and E.
Statement 2 ALONE is sufficient. Choice B is the answer.
Chapter doubts & questions for Sequences - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Sequences - 35 Days Preparation for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
35 Days Preparation for GMAT
171 videos|269 docs|181 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









