All Exams >
GMAT >
35 Days Preparation for GMAT >
All Questions
All questions of Quadratic Equations for GMAT Exam
If one of the roots of the quadratic equation x2 + bx + 98 = 0 is the average (arithmetic mean) of the roots of the equation x2 + 28x – 588 = 0, what is the other root of the equation x2 + bx + 98 = 0?- a)-7
- b)−5/2
- c)5/2
- d)7
- e)21
Correct answer is option 'A'. Can you explain this answer?
If one of the roots of the quadratic equation x2 + bx + 98 = 0 is the average (arithmetic mean) of the roots of the equation x2 + 28x – 588 = 0, what is the other root of the equation x2 + bx + 98 = 0?
a)
-7
b)
−5/2
c)
5/2
d)
7
e)
21

|
Pranab Dasgupta answered |
Given
To Find: value of n?
Approach
- We know that the product of roots m and n is equal to c/a
- So, we can write m*n = 98, i.e. n = 98/m
- So, for finding n, we need to find m
- We are given that m = (p+q)/2
- We know that sum of roots of the quadratic equation is −b/a
- We will use this relation to find the value of p + q and hence the value of m
Hence, the other root of the equation x2 + bx + 98 = 0 is -7
Answer: A
If p = – 7 and q = 12 and x2+px+q=0, then the value of ‘x’ is- a)– 3 and 4
- b)3 and 4
- c)3 and – 4
- d)– 3 and – 4
Correct answer is option 'B'. Can you explain this answer?
If p = – 7 and q = 12 and x2+px+q=0, then the value of ‘x’ is
a)
– 3 and 4
b)
3 and 4
c)
3 and – 4
d)
– 3 and – 4

|
Kalyan Nair answered |
Understanding the Quadratic Equation
To solve the equation x² + px + q = 0, we substitute the values of p and q. Given p = 7 and q = 12, the equation becomes:
x² + 7x + 12 = 0
Factoring the Quadratic
Next, we need to factor the quadratic equation. We look for two numbers that multiply to +12 (the constant term) and add up to +7 (the coefficient of x). The numbers that meet these criteria are:
- 3 and 4
Thus, we can express the equation as:
(x + 3)(x + 4) = 0
Finding the Roots
To find the values of x, we set each factor equal to zero:
1. x + 3 = 0 → x = -3
2. x + 4 = 0 → x = -4
However, there seems to be a misunderstanding in the initial problem statement regarding the roots. The correct roots of the equation x² + 7x + 12 = 0 are:
-3 and -4, not 3 and 4.
Conclusion
The correct answer to the equation x² + 7x + 12 = 0 is:
- x = -3
- x = -4
So, the correct roots do not match the options provided. The options mentioned (3 and 4) are incorrect based on the calculations performed.
To solve the equation x² + px + q = 0, we substitute the values of p and q. Given p = 7 and q = 12, the equation becomes:
x² + 7x + 12 = 0
Factoring the Quadratic
Next, we need to factor the quadratic equation. We look for two numbers that multiply to +12 (the constant term) and add up to +7 (the coefficient of x). The numbers that meet these criteria are:
- 3 and 4
Thus, we can express the equation as:
(x + 3)(x + 4) = 0
Finding the Roots
To find the values of x, we set each factor equal to zero:
1. x + 3 = 0 → x = -3
2. x + 4 = 0 → x = -4
However, there seems to be a misunderstanding in the initial problem statement regarding the roots. The correct roots of the equation x² + 7x + 12 = 0 are:
-3 and -4, not 3 and 4.
Conclusion
The correct answer to the equation x² + 7x + 12 = 0 is:
- x = -3
- x = -4
So, the correct roots do not match the options provided. The options mentioned (3 and 4) are incorrect based on the calculations performed.
In the equation ax2 + bx + c = 0, where a, b and c are constants and a ≠ 0, what is the value of b?(1) 3 and 4 are roots of the equation.(2) The product of the roots of the equation is 12.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'E'. Can you explain this answer?
In the equation ax2 + bx + c = 0, where a, b and c are constants and a ≠ 0, what is the value of b?
(1) 3 and 4 are roots of the equation.
(2) The product of the roots of the equation is 12.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Pranav Das answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given equation is
ax2+bx+c=0
It is also given that a, b and c are constants and that a≠0.
We need to find the value of b.
Step 3: Analyze Statement 1
It is given that 3 and 4 are the roots of the equation.
We know that for a quadratic equation
ax2+bx+c=0
ax2+bx+c=0
Sum of roots = −b/a
Product of roots = c/a
Therefore, we have:
−ba = 3 + 4 = 7………..(I)
c/ a = 3 * 4 = 12 …………(II)
Note that these are two linear equations in three variables. So we cannot solve exclusively for b.
Statement 1 alone is not sufficient to arrive at a unique answer.
Step 4: Analyze Statement 2
It is given that the product of roots is 12.
Therefore, we have:
c/a = 12 …….(III)
Notice that (III) is a single linear equation in two variables. Moreover, it doesn’t provide any information about b.
So statement 2 alone is not sufficient to arrive at a unique answer.
Step 5: Analyze Both Statements Together (if needed)
Now let us look at both the statements together.
Statement 1 gives us (I) and (II)
Statement 2 gives us (III).
However, notice that (III) is essentially same as (II).
In other words, we are simply left with (I) and (II) (essentially the same situation as in statement 1).
Therefore statement 1 and statement 2 combined together are not sufficient to arrive at a unique answer.
Answer: Option (E)
The angry Arjun carried some arrows for fighting with Bheeshma. With half the arrows, he cut down the arrows thrown by Bheeshma on him and with six other arrows he killed the rath driver of Bheeshma. With one arrow each he knocked down respectively the rath, flag and bow of Bheeshma. Finally with one more than four times the square root of arrows he laid Bheeshma unconscious on an arrow bed. The total number of arrows that Arjun had is- a)80
- b)100
- c)96
- d)120
Correct answer is option 'B'. Can you explain this answer?
The angry Arjun carried some arrows for fighting with Bheeshma. With half the arrows, he cut down the arrows thrown by Bheeshma on him and with six other arrows he killed the rath driver of Bheeshma. With one arrow each he knocked down respectively the rath, flag and bow of Bheeshma. Finally with one more than four times the square root of arrows he laid Bheeshma unconscious on an arrow bed. The total number of arrows that Arjun had is
a)
80
b)
100
c)
96
d)
120

|
Prateek Gupta answered |
Therefore, Arjun had 100 arrows.
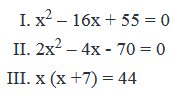 Given the three quadratic equations above, which pair of equations has at least one common root?
Given the three quadratic equations above, which pair of equations has at least one common root?- a)I and II
- b)II and III
- c)I and III
- d)I, II and III
- e)None of the above
Correct answer is option 'E'. Can you explain this answer?
Given the three quadratic equations above, which pair of equations has at least one common root?
a)
I and II
b)
II and III
c)
I and III
d)
I, II and III
e)
None of the above

|
Nandita Chauhan answered |
Given
- Three quadratic equations:
- x2 – 16x + 55 = 0
- 2x2 – 4x - 70 = 0
- x (x +7) = 44
To Find: Which pair of equations has at least one common root?
Approach
- As we need to find the common roots among the equation, we will solve each quadratic equation to find their roots and then find the pair of equations that have at least one common root.
Working Out
So, the roots of Equations I, II and III are (5, 11), (-5, 7) and (-11, 4) respectively.
Hence, none of the equations have even one root in common.
Answer: E
In a cricket match Kumble took three wickets less than twice the number of wickets taken by Srinath. The product of the number of wickets taken by these two is 20, then the number of wickets taken by Kumble is- a)2
- b)4
- c)10
- d)5
Correct answer is option 'D'. Can you explain this answer?
In a cricket match Kumble took three wickets less than twice the number of wickets taken by Srinath. The product of the number of wickets taken by these two is 20, then the number of wickets taken by Kumble is
a)
2
b)
4
c)
10
d)
5

|
Prateek Gupta answered |
Explanation:
Let the number of wickets taken by Srinath be x then the number of wickets taken by Kumble will be 2x−3
According to question, x(2x−3)=20
According to question, x(2x−3)=20
What is the number of integral solutions of the equation 2x2 – 3x – 2 = 0?- a)0
- b)1
- c)2
- d)3
- e)4
Correct answer is option 'B'. Can you explain this answer?
What is the number of integral solutions of the equation 2x2 – 3x – 2 = 0?
a)
0
b)
1
c)
2
d)
3
e)
4

|
EduRev GATE answered |
- Using the quadratic formula:
- (3 ± √25) /4
- The two roots are:
- 8 /4 = 2
- -2 /4 = -1⁄2
- Since only x = 2 is an integer, the number of integral solutions is: 1
Edward invested five-ninths of his money at an annual rate of 2r% compounded semi-annually, and the remaining money at an annual rate of r% compounded annually. If after one year, Edward’s money had grown by one-thirds, the value of r is equal to which of the following?- a)10%
- b)15%
- c)20%
- d)25%
- e)33%
Correct answer is option 'C'. Can you explain this answer?
Edward invested five-ninths of his money at an annual rate of 2r% compounded semi-annually, and the remaining money at an annual rate of r% compounded annually. If after one year, Edward’s money had grown by one-thirds, the value of r is equal to which of the following?
a)
10%
b)
15%
c)
20%
d)
25%
e)
33%

|
Tanishq Choudhury answered |
Given: Let the total money be y
- First Investment:
-
-
- Rate of interest = 2r% p.a. compounded every 6 months = r% per 6-months
- Time = 1 year
-
- Second Investment:
-
-
- Rate of interest = r% p.a.
- Time = 1 year
-
- Total Interest earned in 1 year
To find: The value of r
Approach
1. Total interest earned in 1 year = (Interest earned from 1st investment) + (Interest earned from 2nd investment)
i. In the given time frame of 1 year, the 1st investment will pay interest twice (since this investment pays interest every 6 months). So, the formula for compound interest will be applicable for the 1st investment
ii. The 2nd investment pays interest after 1 year. Since the given time frame is also 1 year, this investment will yield simple interest
2. The only unknown in the above equation will be r. So, using this equation, we can find the value of r
Working Out
- Amount of the first investment after 1 year
- Compound Interest earned from 1st investment
- Calculating the interest earned from the 2nd investment:
- Simple interest earned from 2nd investment =
- So, Total interest earned in 1 year =
- Multiplying both sides of the above equation with 9/y :
- Simple interest earned from 2nd investment =
- Rejecting the negative value since the money is given to have grown.
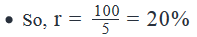
Looking at the answer choices, we see that Option C is correct
(Note: You could also have solved this question by framing the first equation in terms of the amount that each investment grows to, as under:
(Total Amount after 1 year) = (Amount that the 1st investment grows to) + (Amount that the 2nd investment grows to)
This equation leads to a similar calculation and the same result as in the solution above /End of Note)
If x2+4x+p=13 , where p is a constant, what is the product of the roots of this quadratic equation?(1) -2 is one of the roots of the quadratic equation(2) x2+4x+p=13 has equal roots- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If x2+4x+p=13 , where p is a constant, what is the product of the roots of this quadratic equation?
(1) -2 is one of the roots of the quadratic equation
(2) x2+4x+p=13 has equal roots
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Saumya Sharma answered |
Step 1 & Step 2: Understanding the Question statement and Drawing Inferences
Given Info:
- x2+4x+p=13
- Rewriting the above quadratic equation in standard form ax2+bx+c=0
- Subtracting 13 from both sides, we have
⇒ x2+4x+p−13=13−13
⇒ x2+4x+p−13=0
To find:
- We need to find the product of the quadratic equation → x2+4x+p−13=0
- To find the product of the roots:
- We need to know the roots or
- Products of roots of the quadratic equation ax2+bx+c=0 , is given by c/a
- So product of roots of the above quadratic equation will be (p−13)/1 , as →c=p-13 and a=1
- Now since we do not know the value of p-13, we will not be able to determine the product of roots of the quadratic equation.
- Thus we need to analyse the given statements further to determine the value of p, to be able to calculate the product of roots of the quadratic equation.
Step 3: Analyze statement 1 independently
Statement 1:
- -2 is one of the roots of the quadratic equation
- So, -2 will satisfy the given quadratic equation → x2+4x+p−13=0
⇒ (-2)2 + 4(-2) + p - 13 = 0
⇒ 4 - 8 + p - 13 = 0
⇒ p = 17
- Now since we know the value of p, we will be able to find the value of p-13 and thus will be able to calculate the value of product of quadratic equation.
- Hence statement 1 is sufficient to answer the question.
Step 4: Analyze statement 2 independently
Statement 2:
- Quadratic equation has equal roots
- For equal roots, we will use the relation of sum of roots of the quadratic equation to determine the value of the equal root.
- Sum of roots of the quadratic equation ax2+bx+c=0 , is −b/a
- So sum of roots of the quadratic equation → x2+4x+p−13=0 will be −4/1 , where b=4 and a=1
- Now since both roots are equal and the sum of the roots is coming as -4, both roots will thus be equal to – 2 each.
- Now, the equal root → -2, will satisfy the given quadratic equation x2+4x+p−13=0
⇒(-2)2 + 4(-2) + p - 13 = 0
⇒ p=17
- Now since we know the value of p, we will be able to find the value of p-13 and thus will be able to calculate the value of product of quadratic equation.
- Hence statement 2 is sufficient to answer the question
Step 5: Analyze the two statements together
- Since from statement 1 and statement 2, we are able to arrive at a unique answer, combining and analysing statements together is not required.
Hence the correct answer is option D
A poultry farm has only chickens and pigs. When the manager of the poultry counted the heads of the stock in the farm, the number totaled up to 200. However, when the number of legs was counted, the number totaled up to 540. How many more chickens were there in the farm? Note: In the farm, each pig had 4 legs and each chicken had 2 legs.- a)70
- b)120
- c)60
- d)130
- e)80
Correct answer is option 'C'. Can you explain this answer?
A poultry farm has only chickens and pigs. When the manager of the poultry counted the heads of the stock in the farm, the number totaled up to 200. However, when the number of legs was counted, the number totaled up to 540. How many more chickens were there in the farm? Note: In the farm, each pig had 4 legs and each chicken had 2 legs.
a)
70
b)
120
c)
60
d)
130
e)
80

|
Devansh Shah answered |
Step 1 of solving this GMAT Linear Equations Question: Assign Variables and Frame Equations
Let the number of chickens in the farm be 'x'.
Let the number of pigs in the farm be 'y'.
Let the number of pigs in the farm be 'y'.
Each pig or each chicken has one head.
Therefore, number of heads will be the same as the sum of the chickens and pigs in the farm.
The count of the heads in the farm is 200. So, the sum of the number of chickens and pigs is 200.
So, x + y = 200 .... (1)
Therefore, number of heads will be the same as the sum of the chickens and pigs in the farm.
The count of the heads in the farm is 200. So, the sum of the number of chickens and pigs is 200.
So, x + y = 200 .... (1)
Each chicken has 2 legs and each pig has 4 legs
'x' chickens will therefore, have 2x legs and 'y' pigs will have 4y legs.
The count of the legs in the farm is 540. So, the sum of the number of legs of chickens and the number of legs of pigs is 540.
Therefore, 2x + 4y = 540 .... (2)
'x' chickens will therefore, have 2x legs and 'y' pigs will have 4y legs.
The count of the legs in the farm is 540. So, the sum of the number of legs of chickens and the number of legs of pigs is 540.
Therefore, 2x + 4y = 540 .... (2)
Step 2 of solving this GMAT Linear Equations Question: Solve the system of linear equations
Multiply equation (1) by 2. We get 2x + 2y = 400 .... (3)
Subtract equation (3) from equation (2).
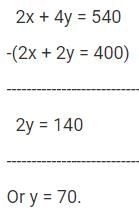
Subtract equation (3) from equation (2).
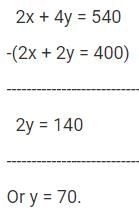
Substitute 'y' as 70 in equation (1).
70 + y = 200. So, x = 130
70 + y = 200. So, x = 130
'x' is the number of chickens in the farm. 'y' is the number of pigs in the farm. So, the farm has 130 chickens and 70 pigs.
Note:The question is "How many more chickens were there in the farm?"
The farm has 130 chickens and 70 pigs. So, the farm has (130 - 70) = 60 more chickens
The farm has 130 chickens and 70 pigs. So, the farm has (130 - 70) = 60 more chickens
Choice C is the correct answer to this linear equations word problem.
The two numbers whose sum is 27 and their product is 182 are- a)12 and 13
- b)12 and 15
- c)14 and 15
- d)13 and 14
Correct answer is option 'D'. Can you explain this answer?
The two numbers whose sum is 27 and their product is 182 are
a)
12 and 13
b)
12 and 15
c)
14 and 15
d)
13 and 14

|
Prateek Gupta answered |
Explanation:Let the one number be xx .As the sum of numbers is 27 , then the other number will be (27−x)(27−x) According to question
A quadratic equation ax2 + bx + c = 0 has two integral roots x1 and x2. If the square of the sum of the roots is 6 greater than the sum of the squares of the roots, which of the following could be the value of the ordered set (a, b, c)?I. (-1, 4, -3)II. (1, 4, 3)III. (3, -10√3, 9) - a)I Only
- b)II Only
- c)III Only
- d)I and II Only
- e)I, II and III Only
Correct answer is option 'D'. Can you explain this answer?
A quadratic equation ax2 + bx + c = 0 has two integral roots x1 and x2. If the square of the sum of the roots is 6 greater than the sum of the squares of the roots, which of the following could be the value of the ordered set (a, b, c)?
I. (-1, 4, -3)
II. (1, 4, 3)
III. (3, -10√3, 9)
a)
I Only
b)
II Only
c)
III Only
d)
I and II Only
e)
I, II and III Only

|
Nitya Kumar answered |
Given
To Find: Values of (a, b, c)
Approach
- For finding the values of (a, b, c), we would first need to find the value of x1 , x2
- We will use the relation
-
- to find out the values of x1 , x2
- Also, we will keep in mind the constraint that x1 , x2 are integers
- Now, we know that
- We will use the relation
- We will use the above relation to find out the possible values of (a, b, c)
As x1 , x2 are integers, the possible cases for (x1 , x2) is either (3,1) or (-3,-1)
- Using (1), (2) and (3), the values of (a, b, c) can be of the form ( a, 4a, 3a) or (a, -4a, 3a)
- Among the options,
- Option-I (-1, 4, -3) is of the form (a, -4a, 3a) and
- Option- II (1, 4, 3) is of the form (a, 4a, 3a)
Hence, options I and II can be the value of ordered set (a, b, c).
Answer: D
If the equation
(1 + t²) x² + 2 t c x + (c² – a²) = 0
has equal roots then which of the following is true?- a)t² = c² (1 + a²)
- b)a² = c² (1 + t²)
- c)c² = a² (1 + t²)
- d) ↵More than one of the above
Correct answer is option 'B'. Can you explain this answer?
If the equation
(1 + t²) x² + 2 t c x + (c² – a²) = 0
has equal roots then which of the following is true?
(1 + t²) x² + 2 t c x + (c² – a²) = 0
has equal roots then which of the following is true?
a)
t² = c² (1 + a²)
b)
a² = c² (1 + t²)
c)
c² = a² (1 + t²)
d)
↵
More than one of the above

|
Chirag Roy answered |
Understanding the Problem
To determine the conditions for the quadratic equation
(1 + t²)x² + 2tcx + (c² - a²) = 0
to have equal roots, we need to analyze its discriminant.
Discriminant Condition
For a quadratic equation Ax² + Bx + C = 0, the condition for equal roots is:
B² - 4AC = 0.
In our case:
- A = 1 + t²
- B = 2tc
- C = c² - a²
We substitute these values into the discriminant condition:
(2tc)² - 4(1 + t²)(c² - a²) = 0.
This simplifies to:
4t²c² - 4(1 + t²)(c² - a²) = 0.
Rearranging the Equation
Dividing through by 4, we get:
t²c² = (1 + t²)(c² - a²).
Expanding the right-hand side results in:
t²c² = c² + t²c² - a² - t²a².
Simplifying this gives:
0 = c² - a² - t²a².
Isolating a²
Rearranging the equation provides:
a² = c²(1 + t²).
This confirms that option B is correct: a² = c²(1 + t²).
Conclusion
Thus, for the quadratic equation to have equal roots, the condition that must hold true is option B.
To determine the conditions for the quadratic equation
(1 + t²)x² + 2tcx + (c² - a²) = 0
to have equal roots, we need to analyze its discriminant.
Discriminant Condition
For a quadratic equation Ax² + Bx + C = 0, the condition for equal roots is:
B² - 4AC = 0.
In our case:
- A = 1 + t²
- B = 2tc
- C = c² - a²
We substitute these values into the discriminant condition:
(2tc)² - 4(1 + t²)(c² - a²) = 0.
This simplifies to:
4t²c² - 4(1 + t²)(c² - a²) = 0.
Rearranging the Equation
Dividing through by 4, we get:
t²c² = (1 + t²)(c² - a²).
Expanding the right-hand side results in:
t²c² = c² + t²c² - a² - t²a².
Simplifying this gives:
0 = c² - a² - t²a².
Isolating a²
Rearranging the equation provides:
a² = c²(1 + t²).
This confirms that option B is correct: a² = c²(1 + t²).
Conclusion
Thus, for the quadratic equation to have equal roots, the condition that must hold true is option B.
r and s are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0 & s >0, such that r is 50 percent greater than s. If the product of the roots of the equation is 150, what is the sum of the roots of the equation?- a)-25
- b)-15
- c)15
- d)25
- e)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
r and s are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0 & s >0, such that r is 50 percent greater than s. If the product of the roots of the equation is 150, what is the sum of the roots of the equation?
a)
-25
b)
-15
c)
15
d)
25
e)
Cannot be determined

|
Hridoy Gupta answered |
To solve this problem, let's start by assigning variables to the roots of the quadratic equation. Let's say that r is one root and s is the other root.
Given that r is 50% greater than s, we can express this relationship as:
r = 1.5s
We are also given that the product of the roots is 150. This means that:
rs = 150
Now, let's express the quadratic equation in terms of the roots:
ax^2 + bx + c = 0
Since r and s are the roots, we can write the equation as:
a(x - r)(x - s) = 0
Expanding this equation, we get:
ax^2 - (ar + as)x + rs = 0
Now, let's substitute the values of r and s into the equation:
ax^2 - (1.5as + as)x + 150 = 0
Simplifying further, we get:
ax^2 - 2.5asx + 150 = 0
Since the quadratic equation is in the form ax^2 + bx + c = 0, we can equate the coefficients to find the sum of the roots:
b/a = -2.5as/a
b = -2.5as
Since the sum of the roots is equal to -b/a, we can substitute the value of b:
Sum of roots = -(-2.5as)/a
Sum of roots = 2.5s
Now, we can substitute the value of rs = 150 into the equation rs = 150:
s(1.5s) = 150
1.5s^2 = 150
Dividing both sides by 1.5, we get:
s^2 = 100
Taking the square root of both sides, we get:
s = 10
Now, substituting the value of s into the equation for the sum of the roots:
Sum of roots = 2.5s
Sum of roots = 2.5(10)
Sum of roots = 25
Therefore, the sum of the roots of the quadratic equation is 25. So, the correct answer is option D) 25.
Given that r is 50% greater than s, we can express this relationship as:
r = 1.5s
We are also given that the product of the roots is 150. This means that:
rs = 150
Now, let's express the quadratic equation in terms of the roots:
ax^2 + bx + c = 0
Since r and s are the roots, we can write the equation as:
a(x - r)(x - s) = 0
Expanding this equation, we get:
ax^2 - (ar + as)x + rs = 0
Now, let's substitute the values of r and s into the equation:
ax^2 - (1.5as + as)x + 150 = 0
Simplifying further, we get:
ax^2 - 2.5asx + 150 = 0
Since the quadratic equation is in the form ax^2 + bx + c = 0, we can equate the coefficients to find the sum of the roots:
b/a = -2.5as/a
b = -2.5as
Since the sum of the roots is equal to -b/a, we can substitute the value of b:
Sum of roots = -(-2.5as)/a
Sum of roots = 2.5s
Now, we can substitute the value of rs = 150 into the equation rs = 150:
s(1.5s) = 150
1.5s^2 = 150
Dividing both sides by 1.5, we get:
s^2 = 100
Taking the square root of both sides, we get:
s = 10
Now, substituting the value of s into the equation for the sum of the roots:
Sum of roots = 2.5s
Sum of roots = 2.5(10)
Sum of roots = 25
Therefore, the sum of the roots of the quadratic equation is 25. So, the correct answer is option D) 25.
The common root of 2x2+x−6 = 0 and x2−3x−10 = 0 is
- a)2
- b)5
- c)-2
- d)3/2
Correct answer is option 'C'. Can you explain this answer?
The common root of 2x2+x−6 = 0 and x2−3x−10 = 0 is
a)
2
b)
5
c)
-2
d)
3/2

|
Chirag Sen answered |
The common root of 2x^2 and x is x.
If p and q are the roots of the quadratic equation ax2 + bx + c = 0, where a*b*c ≠ 0, is the product of p and q greater than 0?(1) |p + q| = |p| + |q|(2) ac > 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If p and q are the roots of the quadratic equation ax2 + bx + c = 0, where a*b*c ≠ 0, is the product of p and q greater than 0?
(1) |p + q| = |p| + |q|
(2) ac > 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Pallavi Sharma answered |
Understanding the Problem
We need to determine if the product of the roots p and q of the quadratic equation ax² + bx + c = 0 is greater than 0, given that a, b, and c are non-zero.
Key Concept
The product of the roots of a quadratic equation is given by the formula p*q = c/a. To determine if p*q > 0, we need to analyze the signs of c and a.
Statement (1): |p + q| = |p| + |q|
This statement implies that both p and q have the same sign. When both roots share the same sign, their product p*q will be positive.
Thus, statement (1) alone is sufficient to conclude that the product of the roots is greater than 0.
Statement (2): ac > 0
This statement means that both a and c are either positive or negative.
- If both a and c are positive, then p*q = c/a > 0.
- If both a and c are negative, then p*q = c/a > 0.
In both cases, the product p*q is greater than 0, making statement (2) alone sufficient as well.
Conclusion
Since both statements independently confirm the product of the roots p and q is greater than 0, we can conclude:
- Statement (1) alone is sufficient.
- Statement (2) alone is sufficient.
Thus, the correct answer is option 'd': EACH statement ALONE is sufficient to answer the question asked.
We need to determine if the product of the roots p and q of the quadratic equation ax² + bx + c = 0 is greater than 0, given that a, b, and c are non-zero.
Key Concept
The product of the roots of a quadratic equation is given by the formula p*q = c/a. To determine if p*q > 0, we need to analyze the signs of c and a.
Statement (1): |p + q| = |p| + |q|
This statement implies that both p and q have the same sign. When both roots share the same sign, their product p*q will be positive.
Thus, statement (1) alone is sufficient to conclude that the product of the roots is greater than 0.
Statement (2): ac > 0
This statement means that both a and c are either positive or negative.
- If both a and c are positive, then p*q = c/a > 0.
- If both a and c are negative, then p*q = c/a > 0.
In both cases, the product p*q is greater than 0, making statement (2) alone sufficient as well.
Conclusion
Since both statements independently confirm the product of the roots p and q is greater than 0, we can conclude:
- Statement (1) alone is sufficient.
- Statement (2) alone is sufficient.
Thus, the correct answer is option 'd': EACH statement ALONE is sufficient to answer the question asked.
Given the equation x2 + bx + c = 0, where b and c are constants, what is the value of c?(1) The sum of the roots of the equation is zero.(2) The sum of the squares of the roots of the equation is equal to 18.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
Given the equation x2 + bx + c = 0, where b and c are constants, what is the value of c?
(1) The sum of the roots of the equation is zero.
(2) The sum of the squares of the roots of the equation is equal to 18.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Kiran Nambiar answered |
Solution:
Given equation is x2 bx c = 0, where b and c are constants
To find: value of c
Statement 1: The sum of the roots of the equation is zero.
Let the roots of the equation be α and β. Then, we know that:
α + β = −b
αβ = c
The sum of the roots is zero, so:
α + β = 0
−b = 0
b = 0
From the equation, we can conclude that c = αβ = 0. This statement alone is sufficient to answer the question.
Statement 2: The sum of the squares of the roots of the equation is equal to 18.
Let the roots of the equation be α and β. Then, we know that:
α + β = −b
αβ = c
We are given that:
α2 + β2 = 18
Squaring the equation α + β = −b, we get:
α2 + 2αβ + β2 = b2
Substituting the values of αβ and b2, we get:
α2 + 2c + β2 = b2
α2 + β2 = b2 − 2c
Substituting the given value of α2 + β2, we get:
18 = b2 − 2c
We can solve for c in terms of b:
c = (b2 − 18)/2
However, we do not know the value of b, so we cannot determine the value of c. This statement alone is not sufficient to answer the question.
Together, statements 1 and 2 give us:
b = 0
α2 + β2 = b2 − 2c = 0 − 2c = −2c
Substituting the given value of α2 + β2, we get:
18 = −2c
c = −9
Therefore, both statements together are sufficient to answer the question. The answer is (C).
Given equation is x2 bx c = 0, where b and c are constants
To find: value of c
Statement 1: The sum of the roots of the equation is zero.
Let the roots of the equation be α and β. Then, we know that:
α + β = −b
αβ = c
The sum of the roots is zero, so:
α + β = 0
−b = 0
b = 0
From the equation, we can conclude that c = αβ = 0. This statement alone is sufficient to answer the question.
Statement 2: The sum of the squares of the roots of the equation is equal to 18.
Let the roots of the equation be α and β. Then, we know that:
α + β = −b
αβ = c
We are given that:
α2 + β2 = 18
Squaring the equation α + β = −b, we get:
α2 + 2αβ + β2 = b2
Substituting the values of αβ and b2, we get:
α2 + 2c + β2 = b2
α2 + β2 = b2 − 2c
Substituting the given value of α2 + β2, we get:
18 = b2 − 2c
We can solve for c in terms of b:
c = (b2 − 18)/2
However, we do not know the value of b, so we cannot determine the value of c. This statement alone is not sufficient to answer the question.
Together, statements 1 and 2 give us:
b = 0
α2 + β2 = b2 − 2c = 0 − 2c = −2c
Substituting the given value of α2 + β2, we get:
18 = −2c
c = −9
Therefore, both statements together are sufficient to answer the question. The answer is (C).
If p and q are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0, what are the roots of the equation ayx2 + byx + cy = 0 where 0 < y ≤ 1?- a)p and q
- b)py and qy
- c)p/yand q/y
- d)y and -y
- e)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
If p and q are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0, what are the roots of the equation ayx2 + byx + cy = 0 where 0 < y ≤ 1?
a)
p and q
b)
py and qy
c)
p/yand q/y
d)
y and -y
e)
Cannot be determined

|
Rajdeep Nair answered |
Given
- ax2+bx+c=0
- has two roots p and q a ≠ 0, 0 < y ≤ 1
To Find
- Roots of ayx2+byx+cy=0
Approach
- To find the roots of the equation ayx2+byx+cy=0 , we will do the following steps:
- Take y common and the get the equation in terms of ax2+bx+c=0
- As we know the roots of ax2+bx+c=0, we will use this knowledge to find the roots of the equation ayx2+byx+cy=0
- Working OutSolving the equation ayx2+byx+cy=0
- ayx2+byx+cy=0
- y(ax2+bx+c)=0
So we have either y = 0 or ax2+bx+c=0
Since we are given that y > 0, y ≠ 0.
Hence ax2+bx+c=0
.As the roots of the equation ax2+bx+c=0 are p and q, the roots of the equation ayx2+byx+cy=0 will also be p and q.
Answer: A
The product of two successive integral multiples of 5 is 1050. Then the numbers are- a)35 and 40
- b)25 and 30
- c)25 and 42
- d)30 and 35
Correct answer is option 'D'. Can you explain this answer?
The product of two successive integral multiples of 5 is 1050. Then the numbers are
a)
35 and 40
b)
25 and 30
c)
25 and 42
d)
30 and 35

|
Tanishq Yadav answered |
The problem:
The product of two successive integral multiples of 5 is 1050. We need to find these two numbers.
Approach:
Let's assume the two numbers as (5x) and (5x + 5), where x is an integer. We can form an equation based on the given information and solve for x.
Solution:
Let's form the equation based on the given information:
(5x) * (5x + 5) = 1050
Expanding the equation:
25x^2 + 25x = 1050
Simplifying the equation:
25x^2 + 25x - 1050 = 0
Factoring the equation:
25(x^2 + x - 42) = 0
Further simplification:
(x^2 + x - 42) = 0
Factoring the quadratic equation:
(x + 7)(x - 6) = 0
Solving for x:
x + 7 = 0 or x - 6 = 0
If x + 7 = 0, then x = -7
If x - 6 = 0, then x = 6
Since we are looking for positive integers, we can discard the negative value of x.
Calculating the numbers:
Using the value of x, we can find the two numbers:
First number = 5x = 5 * 6 = 30
Second number = 5x + 5 = 5 * 6 + 5 = 35
Thus, the two successive integral multiples of 5 that have a product of 1050 are 30 and 35.
Final Answer:
The correct answer is option D, which states that the numbers are 30 and 35.
The product of two successive integral multiples of 5 is 1050. We need to find these two numbers.
Approach:
Let's assume the two numbers as (5x) and (5x + 5), where x is an integer. We can form an equation based on the given information and solve for x.
Solution:
Let's form the equation based on the given information:
(5x) * (5x + 5) = 1050
Expanding the equation:
25x^2 + 25x = 1050
Simplifying the equation:
25x^2 + 25x - 1050 = 0
Factoring the equation:
25(x^2 + x - 42) = 0
Further simplification:
(x^2 + x - 42) = 0
Factoring the quadratic equation:
(x + 7)(x - 6) = 0
Solving for x:
x + 7 = 0 or x - 6 = 0
If x + 7 = 0, then x = -7
If x - 6 = 0, then x = 6
Since we are looking for positive integers, we can discard the negative value of x.
Calculating the numbers:
Using the value of x, we can find the two numbers:
First number = 5x = 5 * 6 = 30
Second number = 5x + 5 = 5 * 6 + 5 = 35
Thus, the two successive integral multiples of 5 that have a product of 1050 are 30 and 35.
Final Answer:
The correct answer is option D, which states that the numbers are 30 and 35.
What is the value of s+t if the equation 3x2 + tx + s has 2 and 3 as its roots?- a)1
- b)2
- c)3
- d)4
- e)5
Correct answer is option 'C'. Can you explain this answer?
What is the value of s+t if the equation 3x2 + tx + s has 2 and 3 as its roots?
a)
1
b)
2
c)
3
d)
4
e)
5

|
EduRev GATE answered |
- Given the equation 3x² + tx + s = 0 with roots 2 and 3:
- Sum of roots: 2 + 3 = 5 ⇒ -t /3 = 5 ⇒ t = -15
- Product of roots: 2 × 3 = 6 ⇒ s /3 = 6 ⇒ s = 18
- s + t = 18 + (-15) = 3
- Answer: 3
If x is an integer and 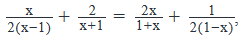 what is the value of x?
what is the value of x?- a)-3
- b)-1
- c)0
- d)2
- e)3
Correct answer is option 'E'. Can you explain this answer?
If x is an integer and 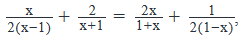 what is the value of x?
what is the value of x?
a)
-3
b)
-1
c)
0
d)
2
e)
3

|
Devika Yadav answered |
Given equation is
And, we need to find the value of x, given that x is an integer.
Step 2 & 3: Finding required values and calculating the final answer
Let us rewriting the last term of (I) to get x-1 in the denominator:
Let us now bring the terms with the same denominator together:
- (x + 1)2 = {2(x – 1)}2
- [(x+1)2-{2(x-1)}2 ]=0 ………….. (II)
- Observe that this is of the form a2 – b2 = (a+b)(a-b)So let us say:a = x + 1b = 2(x – 1) = 2x - 2Therefore:a + b = x + 1 + 2x – 2 = 3x -1a – b = x + 1 - 2x + 2 = -x + 3Therefore we can rewrite (II) as:(3x-1)(3-x)=0
- Putting each factor to zero:
Since it is given that x is an integer,
Thus, x = 3 is the required answer.
Answer: Option (E)
if 2x2 = 24 -x4 and 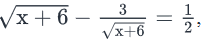 which of the following can be the value of x?
which of the following can be the value of x?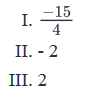
- a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
if 2x2 = 24 -x4 and 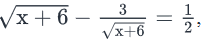 which of the following can be the value of x?
which of the following can be the value of x?
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above

|
Sandeep Mehra answered |
Given:
Approach:
- To answer the question, we need to know the possible values of x.
- So, we’ll first solve Equation 1, then Equation 2 and then find the common roots of both these equations. These will be the possible values of x
- Then, we’ll evaluate the 3 options.
Working Out:
- Solving Equation I
- 2x2 = 24 -x4
- We can factorize this equation as it is, but if powers like x4 intimidate you, then it’s better to substitute x2 with a new variable, say z. That ways, the equation will look simpler: 2z = 24 – z2
- Rearranging the terms: z2 + 2z – 24 = 0
- z2 + 6z – 4z – 24 = 0
- z(z+6) – 4(z+6) = 0
- (z+6)(z-4) = 0
- This means, z = -6 or 4
- But z = x2. So, x2 = -6 or 4
- Perfect square x2 cannot be negative. Therefore, we can reject the negative root.
- So, x2 = 4
- Therefore, x = +2 or -2
- Thus, Equation I has 2 roots: 2 and -2
- Solving Equation II
- This equation looks difficult primarily because it involves a square root term,
. So, for the ease of our calculations, let’s substitute
=y
- So, the equation becomes:
- Multiplying both sides with 2y, we get: 2y2 – 6 = y
- Rearranging the terms: 2y2 – y – 6 = 0
-
- This means, y = -3/2 or y = 2
- Since y =
we can write:
- However, since the square root of a number is always positive, the value of
cannot be -3/2 .
- If you’ve any doubt about this, think: When you write z2 = 16 and then take the square root on both sides, you write: Either z = √16 or z = -√16. Note here that, in the ‘or’ case, you put the minus sign outside the value of √16. This minus sign makes z negative (we get z = -4 in the ‘or’ case) but √16 is always positive (equal to 4).
- Similarly, if we have z2 = x + 6, then on taking the square root on both sides, we will write: Either
or
- z= -
So, z may be positive or negative but
will always be positive.
- So,
=2
- Upon squaring both sides of this equation, we get: x + 6 = 4
- Therefore, x = -2
- Thus, we get a single value of x from Equation II
- Finding the possible values of x
- From Equation I: x = 2 or -2
- From Equation II: x = -2
- So, the value of x that satisfies both equations: x = -2
- Thus, only 1 value of x is possible: {-2}
- Evaluating the 3 options
- Out of the 3 given options, x can only be equal to -2
- Looking at the answer choices, we see that the correct answer is Option B
The area of a rectangle is 28 square centimeter. What is the perimeter of the rectangle?(1) If the length of the rectangle is increased by 10 centimeter and the breadth is decreased by 5 centimeter, the perimeter of the rectangle is eight times the original length of the rectangle.(2) If the length of the rectangle is increased by 350% and the breadth is increased to 350% of the original breadth, the perimeter of the rectangle is 63 centimeters more than the original perimeter of the rectangle.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
The area of a rectangle is 28 square centimeter. What is the perimeter of the rectangle?
(1) If the length of the rectangle is increased by 10 centimeter and the breadth is decreased by 5 centimeter, the perimeter of the rectangle is eight times the original length of the rectangle.
(2) If the length of the rectangle is increased by 350% and the breadth is increased to 350% of the original breadth, the perimeter of the rectangle is 63 centimeters more than the original perimeter of the rectangle.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Prashanth Chawla answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given:
Let the length and breadth of rectangle be L and B respectively
- LB = 28…..............................................(1)
To find: The value of 2(L+B)
- To find perimeter, we need to know the value of L and B.
Step 3: Analyze Statement 1 independently
(1) If the length of the rectangle is increased by 10 centimeter and the breadth is decreased by 5 centimeter, the perimeter of the rectangle is eight times the original length of the rectangle.
- New L = L +10
- New B = B - 5
So,
- New Perimeter = 2(L+10 + B-5)
- 2(L+10 + B-5) = 8L
- 2L + 2B + 10 = 8L
- 6L – 2B – 10 = 0
- 3L – B – 5 = 0
- B = 3L - 5 . . . . . . . . . . . . . . .. . . . .(2)
Substituting (2) in (1):
- 2 values of L (roots) will be obtained from this quadratic equation
Comparing this with the standard quadratic form : ax2 + bx + c = 0, we get : a = 1 ; b = -5/3 ; c = -28/3
- Product of these 2 values = (c/a) −283
-
- Since the product is negative, one root is positive and the other is negative
- The negative root will be rejected
- L, being the length of a rectangle, cannot be negative
- Thus, a unique value of L is obtained
- Using Equation (2), a unique value of B is also obtained
Hence, Statement 1 alone is sufficient.
Step 4: Analyze Statement 2 independently
- If the length of the rectangle is increased by 350% and the breadth is increased to 350% of the original breadth, the perimeter of the rectangle is 63 centimeters more than the original perimeter of the rectangle
- New L = 4.5L
- New B = 3.5B
So,
Substituting (3) in (1):
- 2 values of L (roots) will be obtained from this quadratic equation
Comparing this with the standard quadratic form : ax2 + bx + c = 0, we get :
a = 1 ; b = - 9 ; c = 20
- Product of these 2 values = (c/a) = 20
- Since the product is positive, the two roots are either both positive or both negative
- Sum of roots = (-b/a) = -(-9) = 9
- Since the sum is positive, it means both roots are positive
- Thus, St. 2 leads to 2 values of L
- From Equation (3), 2 values of B will be obtained
- So, 2 values of Perimeter will be obtained.
St. 2 is not sufficient to obtain a unique value of the perimeter.
Step 5: Analyze Both Statements Together (if needed)
Since we get a unique answer in Step 3, this step is not required
Answer: Option A
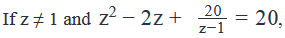 then how many negative values can z take ?
then how many negative values can z take ? - a)None
- b)One
- c)Two
- d)Three
- e)A finite number greater than three
Correct answer is option 'B'. Can you explain this answer?
a)
None
b)
One
c)
Two
d)
Three
e)
A finite number greater than three

|
Prateek Gupta answered |
To Find: Number of negative values of z
Approach:
- Solve the given equation
- Note that the denominator is z - 1.
- To remove the denominator, we will need to multiply each term of this equation with z - 1.
- This will be time consuming (because we will have to multiply each term with z as well as with -1. Example:
and is likely to result in a tedious calculation.
- To simplify this process, we will substitute (z - 1) as x
- Find the value of z
- Count the number of negative values of z
Substitute z - 1 = x
Therefore z = x + 1 ; z - 2 = x -1
Hence
This is a cubic equation (involves x3) and you may feel that you do not know how to solve a cubic equation.
However, before giving up, think about how you solve a quadratic equation? By rewriting the given equation into its factors.
Let’s try if the cubic equation above can be similarly written into factors. We’ll find that the middle term, -21x, can be broken down as under:
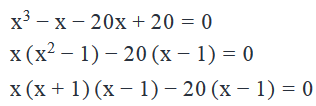
That is
- z - 1 = 1 or 4 or -5
- z = 2 or 5 or -4
- Thus, we get three values of z. However, the question asks specifically about the number of negative values of z.
- Among the 3 possible values of z, we see that only one value of z is negative.
Correct Answer: Option B
If the sum of three consecutive terms of an increasing A.P. is 51 and the product of the first and third of these terms is 273, then the third term is - a)13
- b)9
- c)21
- d)17
Correct answer is option 'C'. Can you explain this answer?
If the sum of three consecutive terms of an increasing A.P. is 51 and the product of the first and third of these terms is 273, then the third term is
a)
13
b)
9
c)
21
d)
17

|
EduRev GATE answered |
- Let 3 consecutive terms A.P is a –d, a , a + d. and the sum is 51
- so, (a –d) + a + (a + d) = 51
- ⇒ 3a –d + d = 51
- ⇒ 3a = 51
- ⇒ a = 17
- The product of first and third terms is 273
- So it stand for ( a –d) (a + d) = 273
- ⇒ a2 –d2 = 273
- ⇒ 172 –d 2 = 273
- ⇒ 289 –d 2 = 273
- ⇒ d 2 = 289 –273
- ⇒ d 2 = 16
- ⇒ d = 4
- Hence the 3rd terms ( a+d )= 17 + 4 = 21
If 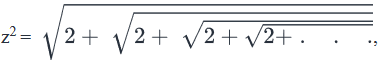 where the given expression extends till infinity, which of the following statements must be true ?I. Two values are possible for zII. 4 - z2 = 2III. z8 = 16
where the given expression extends till infinity, which of the following statements must be true ?I. Two values are possible for zII. 4 - z2 = 2III. z8 = 16 - a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'D'. Can you explain this answer?
If 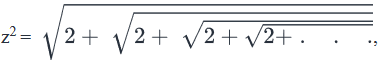
where the given expression extends till infinity, which of the following statements must be true ?
I. Two values are possible for z
II. 4 - z2 = 2
III. z8 = 16
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above

|
Kirti Roy answered |
Given:
To find: Which of the given 3 statements must be true about z?
Approach:
- Looking at the 3 statements, we realize that in order to validate them, we’ll need to know the value of z
- We’re given an expression for z2. Using that expression, we’ll find the value of z
Working Out:
- Finding the value of z
-
- Notice that the series of within within
is never-ending. So, we can write:
-
To make our calculations easy, let’s replace z2 with another variable, say 'y'
- So, we get:
- Now, squaring both sides:
- y2 = 2 + y
- y2 – y – 2 = 0
- (y-2)(y+1) = 0
- So, y = 2 or y = -1
- Since y = z2 and perfect squares are never negative, y cannot be -1
- So, y = z2 = 2
- This means, either z√2 or z-√2
- Checking the validity of the 3 Statements
- Statement I: Two values are possible for z
-
- As we’ve found above, indeed only 2 values are possible for z
- Therefore, this statement is true
- Statement II: 4 - z2 = 2
- As we calculated above, z2 = 2
- So, 4 – z2 = 4 – 2 = 2
- So, this statement too is true
- Statement III: z8 = 16
- Since z2 = 2, (z2)4 = 24
- So, z8 = 16
- Therefore, this statement is true as well
- Looking at the answer choices, we see that the correct answer is Option D
A number x is multiplied with itself and then added to the product of 4 and x. If the result of these two operations is -4, what is the value of x?- a)-4
- b)-2
- c)2
- d)4
- e)Cannot be determined.
Correct answer is option 'B'. Can you explain this answer?
A number x is multiplied with itself and then added to the product of 4 and x. If the result of these two operations is -4, what is the value of x?
a)
-4
b)
-2
c)
2
d)
4
e)
Cannot be determined.

|
Rajdeep Nair answered |
Given
- x∗x+4∗x=−4
- x2 + 4x + 4 = 0
To Find: value of x?
Approach
- As we have a quadratic equation x2+4x+4=0
- , we will solve this equation to find out the value of x
Working Out
x2+4x+4=0
⇒(x+2)2=0
⇒x=−2
Answer: B
If x is a negative number, what is the value of x?(1) 16x2 – 16x – 5 = 0(2) ||4x+3| - 5| = 3- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
If x is a negative number, what is the value of x?
(1) 16x2 – 16x – 5 = 0
(2) ||4x+3| - 5| = 3
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Pranab Dasgupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: x < 0
To find: x = ?
Step 3: Analyze Statement 1 independently
(1) 16x2 – 16x – 5 = 0
x2–x−5/16=0
- 2 values of x (roots) will be obtained from this quadratic equation
- Product of these 2 values = −5/16
-
-
- Since the product is negative, one root is positive and the other is negative
-
- The positive root will be rejected (given: x < 0)
Thus, a unique value of x will be obtained from Statement 1
Statement 1 is sufficient to answer the question.
Step 4: Analyze Statement 2 independently
x= -5/4 We can reject this value as we know that x < 0
Thus, we get 3 possible negative values of x from Statement 2:
Not sufficient to find a unique value of x
Step 5: Analyze Both Statements Together (if needed)
Since we get a unique answer in Step 3, this step is not required
Answer: Option A
If x is equal to 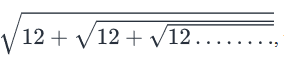 , where the given expressions extend to an infinite number of roots, then what is the value of x?
, where the given expressions extend to an infinite number of roots, then what is the value of x?- a)-3
- b)-4
- c)3
- d)4
- e)12
Correct answer is option 'D'. Can you explain this answer?
If x is equal to 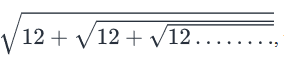 , where the given expressions extend to an infinite number of roots, then what is the value of x?
, where the given expressions extend to an infinite number of roots, then what is the value of x?
a)
-3
b)
-4
c)
3
d)
4
e)
12

|
Saumya Sharma answered |
Given
-
to an infinite terms
- As the value of x is equal to the square root of something, x ≥ 0
To Find:
The value of x
Approach
x= 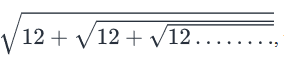 to an infinite terms.
to an infinite terms.
- Since the expression under the root extends infinitely, the expression under the root will be equal to x itself.
- So,
0………….(1)
- By solving this equation and applying the constraint that x ≥0, we will find the value of x
Working Out
a. 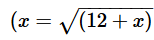
b. Squaring both sides, we have
As we know that x≥ 0, x = 4
Answer: D
Alternate solution
- Once we have deduced that x will be positive the options -3 and -4 are eliminated
- We know √9 is 3. So the value of √(12+ ……) will be more than 3. Now we are left with 4 and 12 in the options
- Now √(12 + …..) cannot give us 12..
- So the answer has be 4.
When a body falls freely under gravity, the distance d covered by it in time t is given by the formula: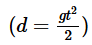 , where g is a constant called acceleration due to gravity.When a ball is dropped from a 16-feet high structure on earth, it takes 1 second to reach the ground. How much time will it take for a ball to reach the ground if it is dropped from a height of 2800 feet on a planet whose acceleration due to gravity is seven times that of earth?
, where g is a constant called acceleration due to gravity.When a ball is dropped from a 16-feet high structure on earth, it takes 1 second to reach the ground. How much time will it take for a ball to reach the ground if it is dropped from a height of 2800 feet on a planet whose acceleration due to gravity is seven times that of earth?- a)1
- b)3
- c)5
- d)10
- e)25
Correct answer is option 'C'. Can you explain this answer?
When a body falls freely under gravity, the distance d covered by it in time t is given by the formula:
When a ball is dropped from a 16-feet high structure on earth, it takes 1 second to reach the ground. How much time will it take for a ball to reach the ground if it is dropped from a height of 2800 feet on a planet whose acceleration due to gravity is seven times that of earth?
a)
1
b)
3
c)
5
d)
10
e)
25

|
Anirban Das answered |
Step 1: Question statement and Inferences
We are given an equation to calculate the distance travelled (d) by a free falling body within a time (t).
It is given that on earth, a ball dropped from a height of 16 feet takes 1 second to reach the ground.
Therefore from (I), we have
16= 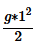
⇒g=32
Thus, we have found the value of acceleration due to gravity for earth.
Let the acceleration due to gravity of the other planet be GP
It is given that GP=7g
⇒GP=7*32……. (II)
Step 2 & 3: Finding required values and calculating the final answer
Once again, using (I) we can write the equation for the free-fall of the ball on the other planet:
2800= 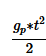
However, from (II), we know that
However, from (II), we know that
GP=7*32
Using this in the above equation, we get,
- t2= 25
- t2 – 25 = 0
- (t -5)(t + 5) = 0
- t = 5 or t = -5
However, t denotes time. Therefore, it cannot have a negative value.
Rejecting the negative value, we get t = 5
Thus, on the other planet, it will take a ball 5 seconds to reach the ground from a height of 2800 feet under conditions of free fall.
Answer: Option (C)
If x and y are non-zero numbers, what is the value of x/y?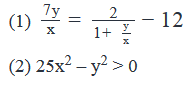
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
If x and y are non-zero numbers, what is the value of x/y?
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Manasa Gupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
Step 3: Analyze Statement 1 independently
Not sufficient to get a unique value of the ratio x/y.
Step 4: Analyze Statement 2 independently
Multiplying both sides of the inequality with will not impact the sign of inequality:
From the Wavy Line Method:
Not sufficient to determine the exact value.
Step 5: Analyze Both Statements Together (if needed)
From Statement 1:
From Statement 2:
Both the values of 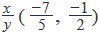 obtained from Statement 1 is less than −1/5
obtained from Statement 1 is less than −1/5
Therefore, both these values satisfy Statement 2
So, we are still not able to determine a unique value of the ratio x/y
Answer: Option E
If integers p, q and r are the roots of the equation x3-7x2+12x = 0, and p < q < r, what is the value of 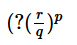 ?
? - a)0
- b)1/3
- c)1
- d)3
- e)4
Correct answer is option 'C'. Can you explain this answer?
If integers p, q and r are the roots of the equation x3-7x2+12x = 0, and p < q < r, what is the value of 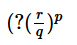 ?
?
a)
0
b)
1/3
c)
1
d)
3
e)
4

|
Telecom Tuners answered |
- Step 1: Question statement and Inferences
- Given equation is x3−7x2+12x=0
- and p, q, r are the roots of this equation.
- We need to find the value of the expression
- . For this we need to find the values of p, q and r by solving the given equation.
- Step 2 & 3: Finding required values and calculating the final answer
- x3−7x2+12x=0
- ⇒x(x2−7x+12)=0 ....(I)
- Note that x2−7x+12
- is a standard form quadratic equation. It can be factorized as follows:
- x2−4x−3x+12=(x−3)(x−4)
- Therefore (I) can be rewritten as:
- x(x-3)(x-4) = 0
- By putting each factor equal to zero, we can find the roots of (I):
- x = 0(Root 1)
- x – 3 = 0
- ⇒ x = 3 (Root 2)
- x – 4 = 0
- ⇒ x = 4 (Root 3)
- Therefore possible values for p, q, r: {0, 3, 4}
- Since it is given that p < q < r, we have:
- p = 0, q = 3 and r =4
- Therefore
=
- When a number is raised to the power zero, we get 1.
- So,
=1
- ⇒
=1
- Answer: Option (C)
What are the roots of the quadratic equation x2 + bx + c = 0 if the roots are distinct and at equal distance from 5 on the number line?(1) The product of the roots of the equation x2 + bx + c = 0 is 21(2) x – 7 is a factor of the expression 7x2 + 7bx + 7c- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
What are the roots of the quadratic equation x2 + bx + c = 0 if the roots are distinct and at equal distance from 5 on the number line?
(1) The product of the roots of the equation x2 + bx + c = 0 is 21
(2) x – 7 is a factor of the expression 7x2 + 7bx + 7c
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Prateek Gupta answered |
Steps 1 & 2: Understand Question and Draw Inferences
- x2+bx+c=0
- Let the distance of the roots of the equation from 5 be d.
- So, the roots will be 5 +d and 5 – d
- Since the 2 roots are distinct, d ≠ 0
- The sum of the roots = (5+d) + (5-d) = 10
- So, −b/a=10
- In the given quadratic equation, a, which denotes the coefficient of x2, is 1.
- So b = -10
- So, the roots will be 5 +d and 5 – d
To Find: As we have assumed the roots of the equation to be (5 +d) and (5 –d), to find the roots, we need to find the value of d
Step 3: Analyze Statement 1 independently
(1) The product of the roots of the equation x2 + bx + c = 0 is 21
- Product of roots = c/a=21
- Since a = 1 in this equation, we can infer that c = 21
- We need to find the roots of x2−10x+21=0
- Since, we know the quadratic equation, we can find the roots of the equation.
Sufficient to answer
Alternate Method:
- Product of roots = (5+d) (5-d) = 21
- 52−d2=21
- d2 = 25 - 21 = 4
d = 2 or -2 - For d = 2
- Roots = 5+2 = 7 and 5-2 = 3
- For d = -2
- Roots = 5-2 = 3 and 5+2 = 7
So, the roots of the equation are 3 and 7
Sufficient to answer
Step 4: Analyze Statement 2 independently
(2) x – 7 is a factor of the expression 7x2 + 7bx + 7c
- x- 7 is a factor of the expression 7(x2+bx+c)
Since 7 is a constant
- (x-7) is a factor of the expression x2+bx+c
Therefore,
- x = 7 is one of the roots of the equation x2+bx+c=0
That is
- 5 + d = 7,
- So, d = 2 and hence the other root is 5 – d = 3. OR
- 5 – d = 7
- So, d = -2 and hence the other root is 5 +(-2) = 3
In both the cases, we get the same values of the roots.
Sufficient to answer
Step 5: Analyze Both Statements Together (if needed)
As we have a unique answer from steps 3 and 4, this step is not required
Answer: D
What is the value of x in the equation x2 + 9 = 6x ?- a)x =1 or x = 3
- b)x = 1 only
- c)x = -1 or x = -3
- d)x = 3 only
- e)No real value of x
Correct answer is option 'D'. Can you explain this answer?
What is the value of x in the equation x2 + 9 = 6x ?
a)
x =1 or x = 3
b)
x = 1 only
c)
x = -1 or x = -3
d)
x = 3 only
e)
No real value of x

|
EduRev GATE answered |
- Given, x2 + 9 = 6x
- ⇒ x2 - 6x + 9 = 0
- ⇒ x2 -3x -3x + 9 = 0
- ⇒ x ( x - 3) - 3 ( x - 3) = 0
- Taking (x-3) common from the equation , we get
- ⇒ (x - 3) (x - 3) = 0
- ⇒ x = 3
If x >0, what is the value of x?(1) x is equal to half of its square root(2) 4x2 + 7x – 2 = 0- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
If x >0, what is the value of x?
(1) x is equal to half of its square root
(2) 4x2 + 7x – 2 = 0
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Nandita Yadav answered |
Steps 1 & 2: Understand Question and Draw Inferences
We are given that x is a positive integer
- x > 0
Step 3: Analyze Statement 1
Writing the information given in statement 1 in an equation form:
x=(√x)/2
Squaring both sides:
x2=x/4
x2−x/4=0 (a standard form Quadratic equation)
x(x−1/4)=0
Now that the equation is in factorized form, we can find the roots.
Either x = 0
Or,
x–1/4=0
x=1/4
Thus, two values of x can satisfy the given equation.
However, we are given that x > 0
- 0 cannot be a value of x.
This means that x=1/4
Thus, a unique value of x is obtained from the information given in Statement 1
SUFFICIENT
Step 4: Analyze Statement 2
We are given a quadratic equation in the standard form:
4x2 + 7x – 2 = 0
We will factorize this equation to find its roots:
4x2 + 8x – x – 2 = 0
- 4x(x + 2) -1 (x+2) = 0
- (4x-1)(x+2) = 0
Now that the given equation has been factorized, we can find the roots by putting each factor equal to zero.
Either
4x – 1 = 0
x=1/4
Or
x + 2 = 0
x = -2
Given: x > 0
Therefore, x cannot have the value -2.
Thus, x=1/4
A unique value of x is obtained from the information given in Statement 2.
SUFFICIENT
Step 5: Analyze Both Statements Together (if needed)
We get a unique answer in steps 3 and4, so this step is not required
Answer: Option (D)
If (x−3)(2x−5)=0 and (x−5/2)(x−4)=0, x = ?
- a)-3
- b)-5/2
- c)5/2
- d)3
- e)4
Correct answer is option 'C'. Can you explain this answer?
If (x−3)(2x−5)=0 and (x−5/2)(x−4)=0, x = ?
a)
-3
b)
-5/2
c)
5/2
d)
3
e)
4

|
Anirban Das answered |
Step 1: Question statement and Inferences
We are given two quadratic equations in x. We will solve both of them and look for a common value of x
Step 2 & 3: Finding required values and calculating the final answer
Approach:
- We observe that both the given quadratic equations are already in factored form.
- By putting each factor of an equation equal to zero, we can find the roots of an equation. So, we will be able to find the two roots of each equation.
- The common root of both equations will be our answer
Implementing the approach:
Finding the roots of the first equation:
(x - 3)(2x - 5)
Either
x - 3 = 0
- x = 3 . . . Root 1A
Or
2x - 5 = 0
- x = 5/2 . . . Root1B
Finding the roots of the second equation:
Either
- x = 5/2 . . . Root 2A
Or
x - 4 = 0
- x = 4 . . . Root 2B
We observe that x=5/2
is a common root of both equations.
- The value of x that satisfies both equations is x=5/2
Answer: Option (C)
if 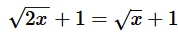 and x is not a positive integer, x = ?
and x is not a positive integer, x = ?- a)0
- b)√2
- c)√3
- d)2√2
- e)4√2
Correct answer is option 'A'. Can you explain this answer?
if 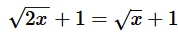 and x is not a positive integer, x = ?
and x is not a positive integer, x = ?
a)
0
b)
√2
c)
√3
d)
2√2
e)
4√2

|
EduRev GATE answered |
Step 1: Question statement and Inferences
Given that x is not a positive integer and we need to find the value of x from the given equation.
Step 2 & 3: Finding required values and calculating the final answer
Given equation is
Squaring on both sides
Squaring on both sides
- 8x =x2
- x2 -8x=0
- x(x -8)=0
Putting each factor to zero, we get:
x = 0 or x = 8
However, since it is already given that x is not a positive integer, x≠8.
Therefore x = 0.
Answer: Option (A)
If x + y = -10 and xy = 16, which of the following statements must be true?
(I) x – y = -6
(II) x2 + y2 = 68
(III) (x-y)2 leaves a remainder of 1 when divided by 7
- a)I only
- b)II only
- c)III only
- d)I and II
- e)II and III
Correct answer is option 'E'. Can you explain this answer?
If x + y = -10 and xy = 16, which of the following statements must be true?
(I) x – y = -6
(II) x2 + y2 = 68
(III) (x-y)2 leaves a remainder of 1 when divided by 7
a)
I only
b)
II only
c)
III only
d)
I and II
e)
II and III

|
Pranav Das answered |
Step 1: Question statement and Inferences
It is given that
x+y=−10 ....(i)
xy=16 ....(ii)
We need to find which of the given statements must be true.
Step 2 & 3: Finding required values and calculating the final answer
Squaring (i) on both sides, we get:
(x+y)2=100
x2+y2+2xy=100
....(iii)
We know that
(x−y)2=x2+y2−2xy
(x−y)2=x2+y2+2xy−4xy
(x−y)2=(x+y)2−4xy
Using (ii) and (iii) we get:
(x−y)2=100−64
(x−y)2=36
⇒(x−y)=±6
Therefore (I) is not a must be true statement.
Now let us look at (II).
(iii) – 2*(ii) gives us:
(x2+y2+2xy)−2xy=100−32
⇒x2+y2=68
Therefore statement II is true.
We already observed above that
(x−y)2=36
We know that
36=35+136=7∗5+1
Therefore
(x−y)2
leaves a remainder of 1 when divided by 7.
Answer: Option (E)
Three years back, a father was 24 years older than his son. At present the father is 5 times as old as the son. How old will the son be three years from now?- a)12 years
- b)6 years
- c)3 years
- d)9 years
- e)27 years
Correct answer is option 'D'. Can you explain this answer?
Three years back, a father was 24 years older than his son. At present the father is 5 times as old as the son. How old will the son be three years from now?
a)
12 years
b)
6 years
c)
3 years
d)
9 years
e)
27 years

|
Pranav Kulkarni answered |
Step 1 of solving this GMAT Linear Equations Question: From words to mathematical equations
Let the age of the son 3 years back be 'x' years.
Information 1: Three years back, a father was 24 years older than his son.
Therefore, the age of the father 3 years back was (x + 24).
Information 1: Three years back, a father was 24 years older than his son.
Therefore, the age of the father 3 years back was (x + 24).
If the age of the son 3 years back was 'x' years, the present age of the son is x + 3.
Present age of father = x + 24 + 3
Present age of father = x + 24 + 3
Information 2: The father is at present 5 times as old as the son.
i.e., (x + 24 + 3) = 5(x + 3)
Or x + 27 = 5x + 15
Or 4x = 12 or x = 3.
i.e., (x + 24 + 3) = 5(x + 3)
Or x + 27 = 5x + 15
Or 4x = 12 or x = 3.
Step 2 of solving this GMAT Algebra Word Problem: From unknown to the answer
x was the age of the son 3 years back.
Therefore, the son was 3 years old 3 years back.
Therefore, the son was 3 years old 3 years back.
The question is "How old will the son be three years from now?"
If the son was 3 years old, 3 years back, the son is 6 years old now.
Hence, he will be 9 years old three years from now.
If the son was 3 years old, 3 years back, the son is 6 years old now.
Hence, he will be 9 years old three years from now.
Choice D is the correct answer.
x2 + bx + 72 = 0 has two distinct integer roots; how many values are possible for 'b'?- a)3
- b)12
- c)6
- d)24
- e)8
Correct answer is option 'B'. Can you explain this answer?
x2 + bx + 72 = 0 has two distinct integer roots; how many values are possible for 'b'?
a)
3
b)
12
c)
6
d)
24
e)
8

|
Pranab Dasgupta answered |
In quadratic equations of the form ax2 + bx + c = 0. - b/a represents the sum of the roots of the quadratic equation and c/a represents the product of the roots of the quadratic equation.
In the equation given a = 1, b = b and c = 72
So, the product of roots of the quadratic equation = 72/1 = 72
And the sum of roots of this quadratic equation = -b/1 = -b
We have been asked to find the number of values that 'b' can take.
If we list all possible combinations for the roots of the quadratic equation, we can find out the number of values the sum of the roots of the quadratic equation can take.
Consequently, we will be able to find the number of values that 'b' can take.
So, the product of roots of the quadratic equation = 72/1 = 72
And the sum of roots of this quadratic equation = -b/1 = -b
We have been asked to find the number of values that 'b' can take.
If we list all possible combinations for the roots of the quadratic equation, we can find out the number of values the sum of the roots of the quadratic equation can take.
Consequently, we will be able to find the number of values that 'b' can take.
The question states that the roots are integers.
If the roots are r1 and r2, then r1 * r2 = 72, where both r1 and r2 are integers.
Possible combinations of integers whose product equal 72 are : (1, 72), (2, 36), (3, 24), (4, 18), (6, 12) and (8, 9) where both r1 and r2 are positive. 6 combinations.
If the roots are r1 and r2, then r1 * r2 = 72, where both r1 and r2 are integers.
Possible combinations of integers whose product equal 72 are : (1, 72), (2, 36), (3, 24), (4, 18), (6, 12) and (8, 9) where both r1 and r2 are positive. 6 combinations.
For each of these combinations, both r1 and r2 could be negative and their product will still be 72.
i.e., r1 and r2 can take the following values too : (-1, -72), (-2, -36), (-3, -24), (-4, -18), (-6, -12) and (-8, -9). 6 combinations.
i.e., r1 and r2 can take the following values too : (-1, -72), (-2, -36), (-3, -24), (-4, -18), (-6, -12) and (-8, -9). 6 combinations.
Therefore, 12 combinations are possible where the product of r1 and r2 is 72.
Hence, 'b' will take 12 possible values.
Hence, 'b' will take 12 possible values.
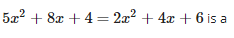
- a)quadratic equation
- b)constant
- c)cubic equation
- d)linear equation
Correct answer is option 'A'. Can you explain this answer?
a)
quadratic equation
b)
constant
c)
cubic equation
d)
linear equation

|
Prateek Gupta answered |
Here, the degree is 2, therefore it is a quadratic equation.
For a quadratic equation, both the product of the roots and the sum of the roots are prime numbers less than 10. If both the roots are integers, what is the difference between the roots?- a)1
- b)2
- c)4
- d)6
- e)Cannot be determined.
Correct answer is option 'A'. Can you explain this answer?
For a quadratic equation, both the product of the roots and the sum of the roots are prime numbers less than 10. If both the roots are integers, what is the difference between the roots?
a)
1
b)
2
c)
4
d)
6
e)
Cannot be determined.

|
Saumya Sharma answered |
Given
- Let the roots be p and q, where p, q are integers
- p + q = prime number less than 10
- p + q = {2, 3, 5, 7}
- p*q = prime number less than 10
- So, p*q = {2, 3, 5, 7}
- Since the product of integers p and q is positive, this means that p and q are either both positive or both negative
- But since p + q is positive, this means that p and q cannot both be negative.
- Therefore p, q > 0
To Find: Value of |p – q|?
- Note: we wrote the expression for difference between the roots as |p-q| and not simply p – q, because at this point, we do not know which of the 2 roots is bigger. By asking about the difference between the 2 roots, the question is asking us to find the value of (Bigger Root – Smaller Root)
Approach
- To find the value of p – q, we need to find the value of p and q.
- We know that pq = {2, 3, 5, 7}, i.e. product of two positive integers is prime, Now, the only possible way in which a prime number can be expressed as a product of two positive integers is (Prime number * 1)
- Using the above information, we can find the possible values of (p, q) = (Prime number, 1), irrespective of the order (that is, irrespective of whether p = Prime Number and q = 1 or vice-versa).
- Finally, we’ll eliminate those values of (p,q) for which p + q is not prime
Working Out
1. As pq = {2, 3, 5, 7}, possible values of (p, q) can be:
- (p, q) = (2, 1) or (3, 1) or (5, 1) or (7, 1)
2. Checking if the sum p + q is prime for these possible values of (p,q):
- If (p, q) = (2, 1), p + q = 3, which is prime
- If (p, q) = (3, 1), p + q = 4, which is not prime
- If (p, q) = (5, 1), p + q = 6, which is not prime
- If (p, q) = (7, 1), p + q = 8, which is not prime
3. Hence, the only possible case where both pq and p + q are prime is when (p, q) = (2, 1), irrespective of the order.
4. So, p – q = 2 – 1 = 1
Answer: A
Chapter doubts & questions for Quadratic Equations - 35 Days Preparation for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Quadratic Equations - 35 Days Preparation for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
35 Days Preparation for GMAT
171 videos|269 docs|181 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily