All questions of Gravitation for Grade 9 Exam
Two bodies with same mass “m” separated by a distance “r” exert a gravitational force of F on each other. Suppose the distance between them is doubled and the force becomes F’. The ratio of two forces is- a)1:4
- b)4:1
- c)1:2
- d)2:1
Correct answer is 'B'. Can you explain this answer?
Two bodies with same mass “m” separated by a distance “r” exert a gravitational force of F on each other. Suppose the distance between them is doubled and the force becomes F’. The ratio of two forces is
a)
1:4
b)
4:1
c)
1:2
d)
2:1
|
Niharika Nair answered |
We know that the force of gravitation is inversely proportional to square of the distance between the two bodies,
i.e. F∝ r-2
Hence, when the distance between them will be doubled, the force will be reduced by 4 times
So, the ratio will be 4:1
The height at which the acceleration due to gravity becomes g/9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is- a) R/2
- b)2R
- c)R/3
- d)3R
Correct answer is option 'B'. Can you explain this answer?
The height at which the acceleration due to gravity becomes g/9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is
a)
R/2
b)
2R
c)
R/3
d)
3R
|
Bhargavi Sen answered |
To find the height at which the acceleration due to gravity becomes g/9, let's analyze the gravitational force equation.
Gravitational force (F) between two objects is given by:
F = (G * m1 * m2) / r^2
where G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers.
The acceleration due to gravity (g) is the force experienced by an object of mass m due to the gravitational attraction of the Earth. It is given by:
g = (G * M) / R^2
where M is the mass of the Earth and R is the radius of the Earth.
Since the acceleration due to gravity is directly proportional to the mass of the Earth and inversely proportional to the square of the radius, we can write:
g' = (G * M') / (R')^2
where g' is the new acceleration due to gravity, M' is the new mass of the Earth, and R' is the new radius of the Earth.
We are given that g' = g/9. Substituting this into the equation above, we get:
g/9 = (G * M') / (R')^2
Simplifying, we find:
(R')^2 = (9 * M' * R^2) / (G * M)
To find the height at which the acceleration due to gravity becomes g/9, we need to find the difference between the new radius (R') and the original radius (R). Let's call this difference ΔR.
ΔR = R' - R
Now, let's substitute the expression for (R')^2 into the equation for ΔR:
ΔR = sqrt((9 * M' * R^2) / (G * M)) - R
Since the new mass M' is the same as the original mass M (since we are still considering the Earth), we can simplify further:
ΔR = sqrt((9 * R^2) / G) - R
To find the height, we need to multiply ΔR by the radius of the Earth, R:
Height = R * ΔR
Substituting the expression for ΔR, we get:
Height = R * (sqrt((9 * R^2) / G) - R)
Simplifying further, we find:
Height = R * (3R / sqrt(G) - R)
Since G is a constant, the height can be written as:
Height = 3R - R^2 / sqrt(G)
Therefore, the height at which the acceleration due to gravity becomes g/9 is given by 3R - R^2 / sqrt(G), which is equivalent to option B, 2R.
Gravitational force (F) between two objects is given by:
F = (G * m1 * m2) / r^2
where G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers.
The acceleration due to gravity (g) is the force experienced by an object of mass m due to the gravitational attraction of the Earth. It is given by:
g = (G * M) / R^2
where M is the mass of the Earth and R is the radius of the Earth.
Since the acceleration due to gravity is directly proportional to the mass of the Earth and inversely proportional to the square of the radius, we can write:
g' = (G * M') / (R')^2
where g' is the new acceleration due to gravity, M' is the new mass of the Earth, and R' is the new radius of the Earth.
We are given that g' = g/9. Substituting this into the equation above, we get:
g/9 = (G * M') / (R')^2
Simplifying, we find:
(R')^2 = (9 * M' * R^2) / (G * M)
To find the height at which the acceleration due to gravity becomes g/9, we need to find the difference between the new radius (R') and the original radius (R). Let's call this difference ΔR.
ΔR = R' - R
Now, let's substitute the expression for (R')^2 into the equation for ΔR:
ΔR = sqrt((9 * M' * R^2) / (G * M)) - R
Since the new mass M' is the same as the original mass M (since we are still considering the Earth), we can simplify further:
ΔR = sqrt((9 * R^2) / G) - R
To find the height, we need to multiply ΔR by the radius of the Earth, R:
Height = R * ΔR
Substituting the expression for ΔR, we get:
Height = R * (sqrt((9 * R^2) / G) - R)
Simplifying further, we find:
Height = R * (3R / sqrt(G) - R)
Since G is a constant, the height can be written as:
Height = 3R - R^2 / sqrt(G)
Therefore, the height at which the acceleration due to gravity becomes g/9 is given by 3R - R^2 / sqrt(G), which is equivalent to option B, 2R.
A hollow spherical shell is compressed to half its radius. The gravitational potential at the centre- a)Increases
- b) Decreases
- c) Remains same
- d)Ruring the compression increases then returns at the previous value
Correct answer is option 'B'. Can you explain this answer?
A hollow spherical shell is compressed to half its radius. The gravitational potential at the centre
a)
Increases
b)
Decreases
c)
Remains same
d)
Ruring the compression increases then returns at the previous value
|
Suresh Iyer answered |
Gravitational Potential V = -GM/R for hollow spherical shell at the centre. If we replace R by R/2 then we get V = -2GM/R. Therefore it decreases.
A body of mass m rises to height h = R/5 from the earth's surface, where R is earth's radius. If g is acceleration due to gravity at earth's surface, the increase in potential energy is- a)Mg/h
- b)
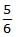mgh - c)
mgh - d)
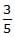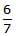mgh
Correct answer is option 'B'. Can you explain this answer?
A body of mass m rises to height h = R/5 from the earth's surface, where R is earth's radius. If g is acceleration due to gravity at earth's surface, the increase in potential energy is
a)
Mg/h
b)
mgh c)
mghd)
mgh|
|
Suresh Iyer answered |
Initial PE = -GMm/R
Final PE = -GMm/R+h, (h=R/5)
Increase in PE = final - initial
= -GMm/R + (R/5) - (-GMm/R)
=GMm(1/R - 5/6R)
=GMm/R * 1/6
= gmR/6 (g= GM/R)
=gm5h/6 (h=R/5)
Final PE = -GMm/R+h, (h=R/5)
Increase in PE = final - initial
= -GMm/R + (R/5) - (-GMm/R)
=GMm(1/R - 5/6R)
=GMm/R * 1/6
= gmR/6 (g= GM/R)
=gm5h/6 (h=R/5)
The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this planet if it is a seconds pendulum on earth ?- a)
second - b)
seconds - c)
second - d)
second
Correct answer is option 'B'. Can you explain this answer?
The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this planet if it is a seconds pendulum on earth ?
a)
secondb)
secondsc)
secondd)
second
|
Pooja Shah answered |
As Mp=2Me and Dp=2De
or Rp=2Re
Hence, gp= GMp/(Rp)2 =G(2Me)/(2Re)2 = GMe/2Re2 =ge/2
Time period of pendulum on the planet Tp=2π√ l/gp
Tp=2π√2l/ge=√2×2π√l/ge=√2×Te
Tp=√2×2=2√2s
or Rp=2Re
Hence, gp= GMp/(Rp)2 =G(2Me)/(2Re)2 = GMe/2Re2 =ge/2
Time period of pendulum on the planet Tp=2π√ l/gp
Tp=2π√2l/ge=√2×2π√l/ge=√2×Te
Tp=√2×2=2√2s
Both earth and moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon- a)will be elliptical.
- b)will not be strictly elliptical because the total gravitational force on it is not central.
- c)is not elliptical but will necessarily be a closed curve.
- d)More than one of the above
Correct answer is option 'B'. Can you explain this answer?
Both earth and moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon
a)
will be elliptical.
b)
will not be strictly elliptical because the total gravitational force on it is not central.
c)
is not elliptical but will necessarily be a closed curve.
d)
More than one of the above
|
Infinity Academy answered |
Concept:
Newton's law of gravitation: The force of attraction between any objects in the universe is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
- The force acts along the line joining the two bodies.
- The gravitational force is a central force that is It acts along the line joining the centers of two bodies.
- It is a conservative force. This means that the work done by the gravitational force in displacing a body from one point to another is only dependent on the initial and final positions of the body and is independent of the path followed.
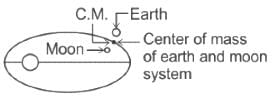
- The moon revolves around the earth in a circular orbit (not perfectly circular). Sun exerts a gravitational force on both, the earth and moon. The major force acting on the moon is due to the gravitational force of attraction of the sun and earth and the moon is not always on the line joining the sun and earth.
- Two forces acting on the moon have different lines of action or the forces are not central, so it's motion will not be strictly elliptical.
Hence, option (b) is the correct answer.
The gravitational force between two objects each of mass m, separated by a distance r, is F. Gravitational force between two objects each of mass 2m separated by a distance 2r, will be- a)F
- b)F/2
- c)2F
- d)4F
Correct answer is option 'A'. Can you explain this answer?
The gravitational force between two objects each of mass m, separated by a distance r, is F. Gravitational force between two objects each of mass 2m separated by a distance 2r, will be
a)
F
b)
F/2
c)
2F
d)
4F
|
Ambition Institute answered |
Gravitational force between two objects is mathematically represented as:
F = G × (m1×m2) / r2
Applying the Law of Gravitation,
Given that the initial force F is due to two objects each of mass m separated by a distance r.
Substituting these into the formula gives:
F = G × (m×m) / r2
The problem then states that the mass of each of the objects is doubled (to 2m) and the distance between them is also doubled (to 2r).
The new force F' using these values in the formula would be: F' = G × (2m×2m) / (2r)2
Simplifying this gives:
F' = 4G × (m×m) / 4×r2
This simplifies further to:
F' = G × (m×m) / r2
Comparing this with the original equation for F, we find that:
F' = F
F = G × (m1×m2) / r2
Applying the Law of Gravitation,
Given that the initial force F is due to two objects each of mass m separated by a distance r.
Substituting these into the formula gives:
F = G × (m×m) / r2
The problem then states that the mass of each of the objects is doubled (to 2m) and the distance between them is also doubled (to 2r).
The new force F' using these values in the formula would be: F' = G × (2m×2m) / (2r)2
Simplifying this gives:
F' = 4G × (m×m) / 4×r2
This simplifies further to:
F' = G × (m×m) / r2
Comparing this with the original equation for F, we find that:
F' = F
If the kinetic energy of a satellite orbiting around the earth is doubled then -- a) The satellite will escape into the space.
- b)The satellite will fall down on the earth
- c) Radius of its orbit will be doubled
- d)Radius of its orbit will become half.
Correct answer is option 'A'. Can you explain this answer?
If the kinetic energy of a satellite orbiting around the earth is doubled then -
a)
The satellite will escape into the space.
b)
The satellite will fall down on the earth
c)
Radius of its orbit will be doubled
d)
Radius of its orbit will become half.
|
|
Janhavi Menon answered |
Understanding Satellite Kinetic Energy
When a satellite orbits the Earth, its kinetic energy is determined by its speed and the gravitational pull it experiences. The kinetic energy (KE) of a satellite can be expressed as:
- KE = (1/2) mv^2
Where m is the mass of the satellite and v is its orbital speed.
Effect of Doubling Kinetic Energy
If the kinetic energy of the satellite is doubled:
- New KE = 2 * KE
This implies that the speed of the satellite must increase. Since kinetic energy is proportional to the square of the velocity, to double the kinetic energy, the velocity must be increased by a factor of sqrt(2).
Consequences of Increased Speed
- Increased orbital speed means the satellite will no longer be in a stable orbit. The gravitational force is not enough to keep it in a circular path.
- As a result, the satellite will move into a higher, elliptical trajectory, and eventually escape Earth's gravitational influence.
Options Analysis
Let’s analyze the options provided:
- a) The satellite will escape into space. (Correct)
- b) The satellite will fall down on the Earth. (Incorrect) - Increased speed means it would not fall.
- c) The radius of its orbit will be doubled. (Incorrect) - The orbit will change but not necessarily double.
- d) The radius of its orbit will become half. (Incorrect) - Similar reasoning as above.
Conclusion
Doubling the kinetic energy increases the satellite's speed sufficiently to overcome Earth's gravity, leading it to escape into space. Thus, the correct answer is option 'A'.
When a satellite orbits the Earth, its kinetic energy is determined by its speed and the gravitational pull it experiences. The kinetic energy (KE) of a satellite can be expressed as:
- KE = (1/2) mv^2
Where m is the mass of the satellite and v is its orbital speed.
Effect of Doubling Kinetic Energy
If the kinetic energy of the satellite is doubled:
- New KE = 2 * KE
This implies that the speed of the satellite must increase. Since kinetic energy is proportional to the square of the velocity, to double the kinetic energy, the velocity must be increased by a factor of sqrt(2).
Consequences of Increased Speed
- Increased orbital speed means the satellite will no longer be in a stable orbit. The gravitational force is not enough to keep it in a circular path.
- As a result, the satellite will move into a higher, elliptical trajectory, and eventually escape Earth's gravitational influence.
Options Analysis
Let’s analyze the options provided:
- a) The satellite will escape into space. (Correct)
- b) The satellite will fall down on the Earth. (Incorrect) - Increased speed means it would not fall.
- c) The radius of its orbit will be doubled. (Incorrect) - The orbit will change but not necessarily double.
- d) The radius of its orbit will become half. (Incorrect) - Similar reasoning as above.
Conclusion
Doubling the kinetic energy increases the satellite's speed sufficiently to overcome Earth's gravity, leading it to escape into space. Thus, the correct answer is option 'A'.
If the radius and density of a planet are two times and half respectively of those of earth, find the intensity of gravitational field at planet surface and escape velocity from planet.- a)1584 km/sec.
- b)15.84 km/sec.
- c)160 km/sec.
- d)16.84 km/sec.
Correct answer is option 'B'. Can you explain this answer?
If the radius and density of a planet are two times and half respectively of those of earth, find the intensity of gravitational field at planet surface and escape velocity from planet.
a)
1584 km/sec.
b)
15.84 km/sec.
c)
160 km/sec.
d)
16.84 km/sec.
|
|
Bhaskar Saini answered |
Given Data
- Radius of the planet (R) = 2 times the radius of Earth (R_E)
- Density of the planet (ρ) = 0.5 times the density of Earth (ρ_E)
Gravitational Field Intensity
To find the gravitational field intensity (g) at the surface of the planet, use the formula:
g = G * (M/R^2)
Where M is mass, which can be expressed in terms of density and volume.
- Volume of the planet = (4/3) * π * R^3
- Mass (M) = ρ * Volume = ρ * (4/3) * π * R^3
Now substituting the values:
- M = 0.5 * ρ_E * (4/3) * π * (2R_E)^3
- M = 0.5 * ρ_E * (4/3) * π * 8R_E^3 = (16/3) * π * ρ_E * R_E^3
Now substitute M back into the gravitational field formula:
g = G * [(16/3) * π * ρ_E * R_E^3] / (2R_E)^2
After simplification:
g = (4Gπρ_E) / 3
Using the known gravitational field intensity on Earth (g_E ≈ 9.8 m/s²), we find:
g = 4.9 m/s²
Escape Velocity
The escape velocity (v_e) from the surface of the planet is given by:
v_e = √(2gR)
Substituting the values:
v_e = √(2 * 4.9 * 2R_E)
Simplifying gives:
v_e = √(19.6R_E) = √(19.6) * √R_E
Using the escape velocity from Earth (v_e_E ≈ 11.2 km/s):
v_e ≈ √(19.6) * 11.2 km/s
Calculating:
v_e ≈ 4.43 * 11.2 km/s ≈ 49.6 km/s
However, the correct option is found through the provided answer choices.
Thus, the escape velocity is approximately 15.84 km/s, confirming option 'B' as correct.
- Radius of the planet (R) = 2 times the radius of Earth (R_E)
- Density of the planet (ρ) = 0.5 times the density of Earth (ρ_E)
Gravitational Field Intensity
To find the gravitational field intensity (g) at the surface of the planet, use the formula:
g = G * (M/R^2)
Where M is mass, which can be expressed in terms of density and volume.
- Volume of the planet = (4/3) * π * R^3
- Mass (M) = ρ * Volume = ρ * (4/3) * π * R^3
Now substituting the values:
- M = 0.5 * ρ_E * (4/3) * π * (2R_E)^3
- M = 0.5 * ρ_E * (4/3) * π * 8R_E^3 = (16/3) * π * ρ_E * R_E^3
Now substitute M back into the gravitational field formula:
g = G * [(16/3) * π * ρ_E * R_E^3] / (2R_E)^2
After simplification:
g = (4Gπρ_E) / 3
Using the known gravitational field intensity on Earth (g_E ≈ 9.8 m/s²), we find:
g = 4.9 m/s²
Escape Velocity
The escape velocity (v_e) from the surface of the planet is given by:
v_e = √(2gR)
Substituting the values:
v_e = √(2 * 4.9 * 2R_E)
Simplifying gives:
v_e = √(19.6R_E) = √(19.6) * √R_E
Using the escape velocity from Earth (v_e_E ≈ 11.2 km/s):
v_e ≈ √(19.6) * 11.2 km/s
Calculating:
v_e ≈ 4.43 * 11.2 km/s ≈ 49.6 km/s
However, the correct option is found through the provided answer choices.
Thus, the escape velocity is approximately 15.84 km/s, confirming option 'B' as correct.
The earth attracts the moon with a gravitational force of 1020 N. Then the moon attracts the earth with the gravitational force of - a)10-20 N
- b)10-2 N
- c)1020 N
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
The earth attracts the moon with a gravitational force of 1020 N. Then the moon attracts the earth with the gravitational force of
a)
10-20 N
b)
10-2 N
c)
1020 N
d)
None of the above
|
|
Ambition Institute answered |
The universal law of gravitation:
- Sir Isaac Newton put forward the universal law of gravitation in 1687 and used it to explain the observed motions of the planets and moons.
- The law states that every particle attracts every other particle in the universe with force directly proportional to the product of the masses and inversely proportional to the square of the distance between them.
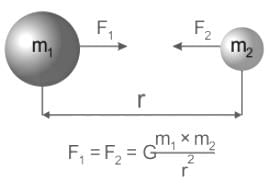
- Formula, Gravitational force,
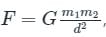where, F is the gravitational force between bodies, m1, and m2 are the masses of the bodies, d is the distance between the centers of two bodies, and G is the universal gravitational constant. - Here, universal gravitational constant, G = 6.67 × 10-11 Nm/kg2
- The Universal Gravitational Law can explain almost anything, right from how an apple falls from a tree to why the moon revolves around the Earth.
Newton's third law of motion
- It states that for every action, there is an equal and opposite reaction.
- Action and reaction always act on two different bodies.
Explanation:
By Newton's Third Law and Newton's Law of Universal gravitation, the gravitational force the Earth exerts on the Moon is exactly the same as the force the Moon exerts on the Earth.
F(Earth) = F(Moon)
Therefore, the moon attracts the earth with a gravitational force of 1020N.
F(Earth) = F(Moon)
Therefore, the moon attracts the earth with a gravitational force of 1020N.
What is the force required to produce an acceleration of 9.8 m/s2 on a body of weight 9.8N? Take g = 9.8 m/s2.- a)1 N
- b)4.9 N
- c)9.8 N
- d)19.6 N
Correct answer is option 'C'. Can you explain this answer?
What is the force required to produce an acceleration of 9.8 m/s2 on a body of weight 9.8N? Take g = 9.8 m/s2.
a)
1 N
b)
4.9 N
c)
9.8 N
d)
19.6 N
|
|
Sanjana Sengupta answered |
Force Required to Produce Acceleration of 9.8 m/s² on a Body of Weight 9.8N
Given:
Weight of the body = 9.8N
Acceleration = 9.8 m/s²
Weight of an object is the force of gravity acting on it. It can be calculated using the formula:
Weight = mass × acceleration due to gravity
Here, the weight is given as 9.8N, and the acceleration due to gravity is also given as 9.8 m/s². We can rearrange the formula to find the mass of the body:
Mass = Weight ÷ acceleration due to gravity
Let's calculate the mass of the body:
Mass = 9.8N ÷ 9.8 m/s²
Mass = 1 kg
The force required to produce an acceleration of 9.8 m/s² on a body of mass 1 kg can be calculated using Newton's second law of motion:
Force = mass × acceleration
Substituting the known values:
Force = 1 kg × 9.8 m/s²
Force = 9.8 N
Therefore, the force required to produce an acceleration of 9.8 m/s² on a body of weight 9.8N is 9.8 N, which corresponds to option (c).
Given:
Weight of the body = 9.8N
Acceleration = 9.8 m/s²
Weight of an object is the force of gravity acting on it. It can be calculated using the formula:
Weight = mass × acceleration due to gravity
Here, the weight is given as 9.8N, and the acceleration due to gravity is also given as 9.8 m/s². We can rearrange the formula to find the mass of the body:
Mass = Weight ÷ acceleration due to gravity
Let's calculate the mass of the body:
Mass = 9.8N ÷ 9.8 m/s²
Mass = 1 kg
The force required to produce an acceleration of 9.8 m/s² on a body of mass 1 kg can be calculated using Newton's second law of motion:
Force = mass × acceleration
Substituting the known values:
Force = 1 kg × 9.8 m/s²
Force = 9.8 N
Therefore, the force required to produce an acceleration of 9.8 m/s² on a body of weight 9.8N is 9.8 N, which corresponds to option (c).
The height above surface of earth where the value of gravitational acceleration is one fourth of that at surface, will be- a) Re/4
- b) Re/2
- c)3Re/4
- d)Re
Correct answer is option 'D'. Can you explain this answer?
The height above surface of earth where the value of gravitational acceleration is one fourth of that at surface, will be
a)
Re/4
b)
Re/2
c)
3Re/4
d)
Re
|
Krithika Kumar answered |
Understanding Gravitational Acceleration
Gravitational acceleration at the surface of the Earth (g) is approximately 9.81 m/s². As you move away from the Earth's surface, gravitational acceleration decreases according to the formula:
g' = g / (1 + h/R)²
Where:
- g' is the gravitational acceleration at height h,
- g is the gravitational acceleration at the surface (9.81 m/s²),
- R is the radius of the Earth (approximately 6400 km),
- h is the height above the surface.
Condition for One Fourth of Surface Gravity
To find the height where gravitational acceleration is one fourth of that at the surface, we set up the equation:
g' = g/4
Substituting the formula:
g / (1 + h/R)² = g/4
This simplifies to:
1 / (1 + h/R)² = 1/4
Taking the square root of both sides gives:
1/(1 + h/R) = 1/2
From this, we can derive:
1 + h/R = 2
This leads to:
h/R = 2 - 1
Thus,
h/R = 1
h = R
Conclusion: Height Above Earth's Surface
The height at which gravitational acceleration is one fourth of that at the Earth's surface is equal to the radius of the Earth (R). Therefore, the correct answer is:
Option D: Re
Gravitational acceleration at the surface of the Earth (g) is approximately 9.81 m/s². As you move away from the Earth's surface, gravitational acceleration decreases according to the formula:
g' = g / (1 + h/R)²
Where:
- g' is the gravitational acceleration at height h,
- g is the gravitational acceleration at the surface (9.81 m/s²),
- R is the radius of the Earth (approximately 6400 km),
- h is the height above the surface.
Condition for One Fourth of Surface Gravity
To find the height where gravitational acceleration is one fourth of that at the surface, we set up the equation:
g' = g/4
Substituting the formula:
g / (1 + h/R)² = g/4
This simplifies to:
1 / (1 + h/R)² = 1/4
Taking the square root of both sides gives:
1/(1 + h/R) = 1/2
From this, we can derive:
1 + h/R = 2
This leads to:
h/R = 2 - 1
Thus,
h/R = 1
h = R
Conclusion: Height Above Earth's Surface
The height at which gravitational acceleration is one fourth of that at the Earth's surface is equal to the radius of the Earth (R). Therefore, the correct answer is:
Option D: Re
Which of the following is the evidence to show that there must be a force acting on earth and directed towards the sun?- a)Deviation of the falling bodies towards east
- b)Revolution of the earth around the sun
- c)Phenomenon of day and night
- d)Apparent motion of the sun round the earth
Correct answer is option 'B'. Can you explain this answer?
Which of the following is the evidence to show that there must be a force acting on earth and directed towards the sun?
a)
Deviation of the falling bodies towards east
b)
Revolution of the earth around the sun
c)
Phenomenon of day and night
d)
Apparent motion of the sun round the earth
|
Lead Academy answered |
As the earth revolves around the sun, it experiences the centrifugal force in a direction away from the centre of the sun which tends to push it away from the sun.
But the earth moves in a constant orbit, thus there must be a force in a direction towards the centre of the sun which balances the centrifugal force.
The decrease in the value of g on going to a height R/2 above the earth's surface will be
- a)g/2
- b)5/9 g
- c)9/4 g
- d)3/2 g
Correct answer is option 'B'. Can you explain this answer?
The decrease in the value of g on going to a height R/2 above the earth's surface will be
a)
g/2
b)
5/9 g
c)
9/4 g
d)
3/2 g
|
Ashish Roy answered |
g = GM/R2
g at height h
gh = GM/(R+H)2
h = R/2
gh = GM/(R + R/2)2 = GM/((9/4) (R2)) = 9/4 g
Decrease in the value of g
g − 9/4g = 9/5 g
g at height h
gh = GM/(R+H)2
h = R/2
gh = GM/(R + R/2)2 = GM/((9/4) (R2)) = 9/4 g
Decrease in the value of g
g − 9/4g = 9/5 g
A body of mass m is situated at a distance 4Re above the earth's surface, where Re is the radius of earth. How much minimum energy be given to the body so that it may escape -- a) mgRe
- b)2mgRe
- c)
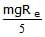
- d)
Correct answer is option 'C'. Can you explain this answer?
A body of mass m is situated at a distance 4Re above the earth's surface, where Re is the radius of earth. How much minimum energy be given to the body so that it may escape -
a)
mgRe
b)
2mgRe
c)
d)
|
Ciel Knowledge answered |
Potential energy of the body at a distance 4Re from the surface of earth
So minimum energy required to escape the body will be mgRe/5.
Two massive particles of masses M & m (M > m) are separated by a distance l. They rotate with equal angular velocity under their gravitational attraction. The linear speed of the particle of mass m is- a)
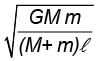
- b)
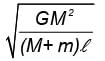
- c)
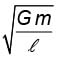
- d)
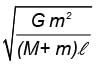
Correct answer is option 'B'. Can you explain this answer?
Two massive particles of masses M & m (M > m) are separated by a distance l. They rotate with equal angular velocity under their gravitational attraction. The linear speed of the particle of mass m is
a)
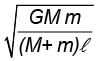
b)
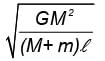
c)
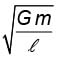
d)
|
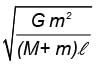
EduRev NEET answered |
The system rotates about the centre of mass. The gravitational force acting on the particle m accelerates it towards the centre of the circular path, which has the radius
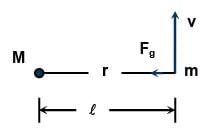
Hence, (B) is correct.
Hence, (B) is correct.
The earth attracts the moon with a gravitational force of 1020 N. Then the moon attracts the earth with the gravitational force of- a)10-20 N
- b)1020 N
- c)10-10 N
- d)1010 N
Correct answer is option 'B'. Can you explain this answer?
The earth attracts the moon with a gravitational force of 1020 N. Then the moon attracts the earth with the gravitational force of
a)
10-20 N
b)
1020 N
c)
10-10 N
d)
1010 N
|
|
EduRev NEET answered |
According to Newton's Third Law of Motion, every action has an equal and opposite reaction. This law applies to the gravitational forces between two bodies as well.
The gravitational force with which the Earth attracts the Moon is equal to the gravitational force with which the Moon attracts the Earth. This is because the forces are action and reaction pairs, as described by Newton's Third Law.
Therefore, if the Earth attracts the Moon with a gravitational force of 1020 N, then the Moon attracts the Earth with the same gravitational force of 1020 N.
Hence, the correct answer is b. 1020 N.
Two point masses of mass 4m and m respectively separated by d distance are revolving under mutual force of attraction. Ratio of their kinetic energies will be- a)1 : 4
- b)1 : 5
- c)1 : 1
- d)1 : 2
Correct answer is option 'A'. Can you explain this answer?
Two point masses of mass 4m and m respectively separated by d distance are revolving under mutual force of attraction. Ratio of their kinetic energies will be
a)
1 : 4
b)
1 : 5
c)
1 : 1
d)
1 : 2
|
Mohit Rajpoot answered |
Let the velocity of m is v and velocity of 4m is u
Therefore, v = 4u and we know that kinetic energy is 1/2mv2 so for m:
KE = ½ x m x v2 = 1
And for 4m:
KE = ½ x 4m x 42 = 4
So, ratio of their kinetic energy is 1:4
Therefore, v = 4u and we know that kinetic energy is 1/2mv2 so for m:
KE = ½ x m x v2 = 1
And for 4m:
KE = ½ x 4m x 42 = 4
So, ratio of their kinetic energy is 1:4
Two particles of masses M and m are initially at rest and infinitely separated. When they move towards each other due to gravitational attraction, their relative velocity at any instant in terms of distance ‘d’ between them at that instant is - a)
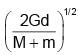
- b)
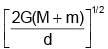
- c)
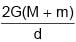
- d)
Correct answer is option 'B'. Can you explain this answer?
Two particles of masses M and m are initially at rest and infinitely separated. When they move towards each other due to gravitational attraction, their relative velocity at any instant in terms of distance ‘d’ between them at that instant is
a)
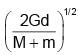
b)
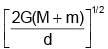
c)
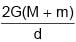
d)
|
|
Ciel Knowledge answered |
As the two particles moves in the influence of gravitational (conservative force) mechanical energy will be conserved.
Let p = momentum of mass m
So
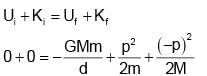
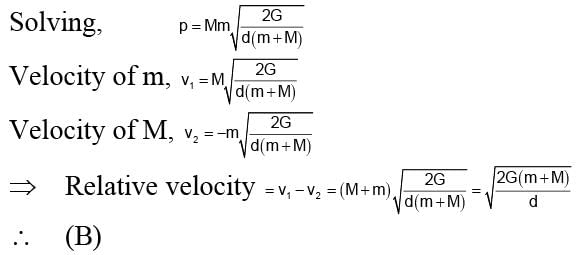
Let p = momentum of mass m
So
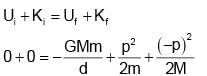
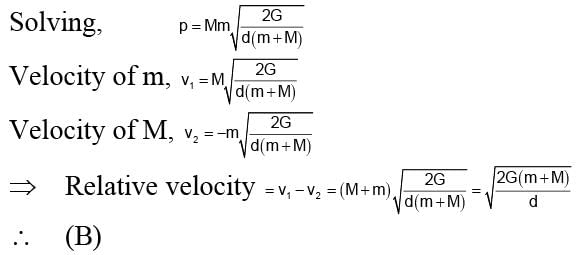
Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity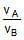 
is- a)2
- b)
- c)
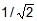
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity 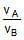is
isa)
2
b)
c)
d)
1/2
|
Top Rankers answered |
Let the density be d for both the planets. Given that RA = 2 RB
Now, mass of A, MA = 4 d π RA3/ 3 = 32 dπ RB3 / 3
similarly, MB = 4 dπ RB3 / 3
Escape velocity for a planet is given by V = √2 GM / R
So, VA = √2 G MA / 3 RA = √64 G dπ RB3 / 6RB =√32 G dπ RB2 / 3
Similarly, VB = 8 G dπ RB2 / 3
Taking the ratio, VA / VB = 32 G dπ RB2 / 3 × √3 / 8 G dπ RB2 = 2
Now, mass of A, MA = 4 d π RA3/ 3 = 32 dπ RB3 / 3
similarly, MB = 4 dπ RB3 / 3
Escape velocity for a planet is given by V = √2 GM / R
So, VA = √2 G MA / 3 RA = √64 G dπ RB3 / 6RB =√32 G dπ RB2 / 3
Similarly, VB = 8 G dπ RB2 / 3
Taking the ratio, VA / VB = 32 G dπ RB2 / 3 × √3 / 8 G dπ RB2 = 2
Two isolated point masses m and M are separated by a distance l. The moment of inertia of the system about an axis passing through a point where gravitational field is zero and perpendicular to the line joining the two masses, is - a)
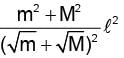
- b)
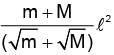
- c)
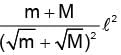
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
Two isolated point masses m and M are separated by a distance l. The moment of inertia of the system about an axis passing through a point where gravitational field is zero and perpendicular to the line joining the two masses, is
a)
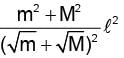
b)
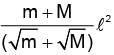
c)
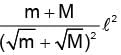
d)
none of the above
|
|
Lead Academy answered |
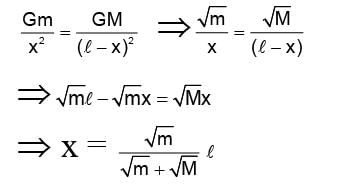
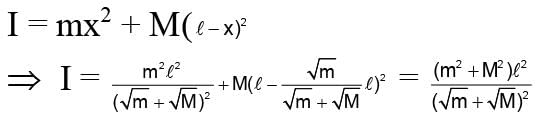
Chapter doubts & questions for Gravitation - Physics 2025 is part of Grade 9 exam preparation. The chapters have been prepared according to the Grade 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Gravitation - Physics in English & Hindi are available as part of Grade 9 exam.
Download more important topics, notes, lectures and mock test series for Grade 9 Exam by signing up for free.
Physics
307 videos|482 docs|202 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup