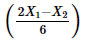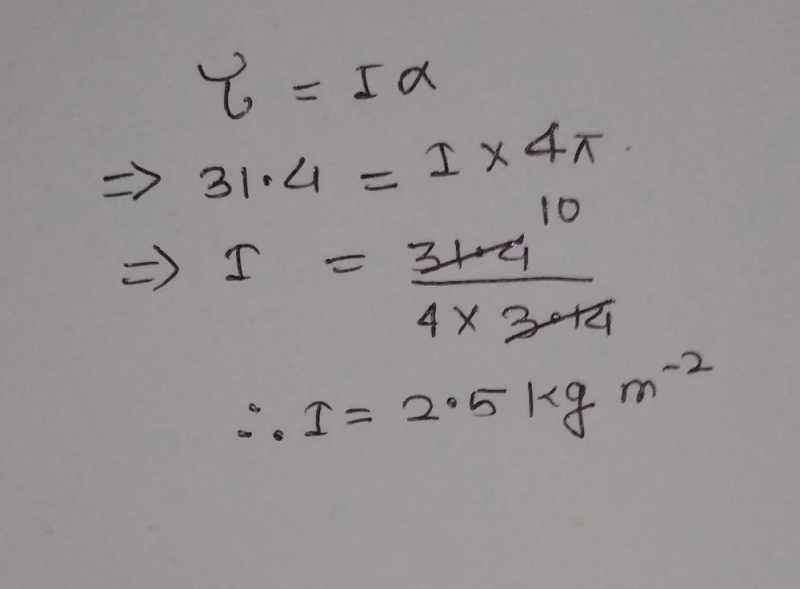All Exams >
JEE >
SRMJEEE Subject Wise & Full Length Mock Tests 2026 >
All Questions
All questions of Engineering for JEE Exam
From a stationary tank of mass 125000 pound a small shell of mass 25 pound is fired with a muzzle velocity of 1000 ft/sec. The tank recoils with a velocity of- a)0.1 ft/sec
- b)0.2 ft/sec
- c)0.4 ft/sec
- d)0.8 ft/sec
Correct answer is option 'B'. Can you explain this answer?
From a stationary tank of mass 125000 pound a small shell of mass 25 pound is fired with a muzzle velocity of 1000 ft/sec. The tank recoils with a velocity of
a)
0.1 ft/sec
b)
0.2 ft/sec
c)
0.4 ft/sec
d)
0.8 ft/sec
|
Cstoppers Instructors answered |
Recoil velocity =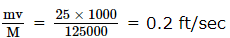 
Which of the following elements has the lowest ionisation potential- a)N
- b)O
- c)F
- d)Ne
Correct answer is option 'B'. Can you explain this answer?
Which of the following elements has the lowest ionisation potential
a)
N
b)
O
c)
F
d)
Ne
|
Vishal Kumar answered |
Oxygen because this is have more substrate such as O2 , O3 etc
Two sides of a triangle are given by the roots of the equation x2 - 5x + 6 =0 and the angle between the sides is π 3 . Then the perimeter of the triangle is- a)5 + √ 2
- b)5 + √3
- c)5 + √5
- d)5 + √7
Correct answer is option 'D'. Can you explain this answer?
Two sides of a triangle are given by the roots of the equation x2 - 5x + 6 =0 and the angle between the sides is π 3 . Then the perimeter of the triangle is
a)
5 + √ 2
b)
5 + √3
c)
5 + √5
d)
5 + √7
|
Krishna Iyer answered |
x2 - 5x + 6 = 0
or x2 - 3x - 2x + 6 = 0
or (x - 3) (x - 2) = 0
or x = 3, 2
So a = 3, b = 2, c = ?, ∠ A = π/3
∴ Perimeter of the triangle = a + b + c = 3 + 2 + √7 = 5 + √7
If (t, 2t), (2t, 6t), (3,8) are collinear, then t =- a)0, 2
- b)5
- c)1 2 , - 1
- d)- 1 2 , 2
Correct answer is option 'A'. Can you explain this answer?
If (t, 2t), (2t, 6t), (3,8) are collinear, then t =
a)
0, 2
b)
5
c)
1 2 , - 1
d)
- 1 2 , 2
|
Vijay Kumar answered |
A(t, 2t), B(2t, 6t), C(3, 8)
Slope of AB = Slope of AC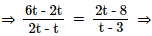
4t(t - 3) = t(2t - 8)
⇒ t(4t - 12 - 2t + 8) = 0 ⇒ t(2t - 4) = 0 ⇒ t = 0, 2
Slope of AB = Slope of AC
4t(t - 3) = t(2t - 8)⇒ t(4t - 12 - 2t + 8) = 0 ⇒ t(2t - 4) = 0 ⇒ t = 0, 2
The first ionisation potentials of four consecutive elements, present in the second period of the periodic table are 8.3, 11.3, 14.5 and 13.6 eV respectively. Which one of the following is the first ionisation potential (in eV) of nitrogen?- a)13.6
- b)11.3
- c)8.3
- d)14.5
Correct answer is option 'D'. Can you explain this answer?
The first ionisation potentials of four consecutive elements, present in the second period of the periodic table are 8.3, 11.3, 14.5 and 13.6 eV respectively. Which one of the following is the first ionisation potential (in eV) of nitrogen?
a)
13.6
b)
11.3
c)
8.3
d)
14.5
|
Yash Gupta answered |
Ans is c because in period energy increase but in nitrogen is hreater energy as compared to oxygen so by this question you see that correct answer is c
A transformer is used to reduce the mains supply of 220 V to 11 V. If the currents in primary and secondary coils are 5 A and 90 A respectively, efficiency of transformer is- a)90%
- b)75%
- c)40%
- d)60%
Correct answer is option 'A'. Can you explain this answer?
a)
90%
b)
75%
c)
40%
d)
60%
|
Preeti Iyer answered |
HT side Power = Vp(Primary Voltage) x Ip(Primary Current) = 220 x 5 = 1100 W
LT side Power = Vs(Secondary Voltage) x Is(Secondary current) = 11 x 90 = 990 W
Loss = HT side Power - LT side Power = 1100-990 = 110 W Or Loss(in %) = (Loss/HT side Power) = 110/1100 = 10%
Efficiency = 100-10 = 90%
If two moles of an ideal gas at 546 K occupy volume of 44.8 L, then pressure must be- a)2 atm
- b)3 atm
- c)4 atm
- d)1 atm
Correct answer is option 'A'. Can you explain this answer?
If two moles of an ideal gas at 546 K occupy volume of 44.8 L, then pressure must be
a)
2 atm
b)
3 atm
c)
4 atm
d)
1 atm
|
Tejas Verma answered |
Ideal gas equation : PV = nRT
n = 2 mol
V = 44.8 L
T = 546 K
R = 0.0821 L atm K-1 mol-1
By putting these values in equation
:
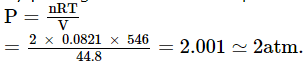
n = 2 mol
V = 44.8 L
T = 546 K
R = 0.0821 L atm K-1 mol-1
By putting these values in equation
:
The length of common chord of circles x2 + y2 + 5x + 7y + 9 = 0 and x2 + y2 + 7x + 5y + 9 = 0 is- a)4
- b)6
- c)3
- d)5
Correct answer is option 'B'. Can you explain this answer?
The length of common chord of circles x2 + y2 + 5x + 7y + 9 = 0 and x2 + y2 + 7x + 5y + 9 = 0 is
a)
4
b)
6
c)
3
d)
5
|
|
Anjali Sen answered |
S1 ≡ x2 + y2 + 5x + 7y + 9 = 0
S2 ≡ x2 + y2 + 7x + 5y + 9 = 0
Common chord is
S1 - S2 = 0
⇒ -2x + 2y = 0
⇒ y - x = 0
Contre and radius of first circle are
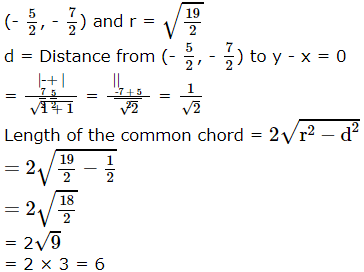
S2 ≡ x2 + y2 + 7x + 5y + 9 = 0
Common chord is
S1 - S2 = 0
⇒ -2x + 2y = 0
⇒ y - x = 0
Contre and radius of first circle are
Al3+ has a lower ionic radius than Mg2+ ion because- a)Mg atom has less number of neutrons than Al
- b)Al3+ has a higher nuclear charge than Mg2+
- c)Their electronegativities are different
- d)Al3+ has a lower ionisation potential than Mg atom
Correct answer is option 'B'. Can you explain this answer?
Al3+ has a lower ionic radius than Mg2+ ion because
a)
Mg atom has less number of neutrons than Al
b)
Al3+ has a higher nuclear charge than Mg2+
c)
Their electronegativities are different
d)
Al3+ has a lower ionisation potential than Mg atom
|
|
Preeti Iyer answered |
Al3+ has a higher nuclear charge (+ 13) and consequently the larger force of attraction by the nucleus for the valence shell electrons than that of Mg2+ (+ 12).
The electric current in a circular coil of two turns produced a magnetic induction of 0.2T at its centre. The coil is unwound and is rewound into a circular coil of four turns. The magnetic induction at the centre of the coil now is, in tesla (if same current flows in the coil)- a)0.2
- b)0.4
- c)0.6
- d)0.8
Correct answer is option 'D'. Can you explain this answer?
The electric current in a circular coil of two turns produced a magnetic induction of 0.2T at its centre. The coil is unwound and is rewound into a circular coil of four turns. The magnetic induction at the centre of the coil now is, in tesla (if same current flows in the coil)
a)
0.2
b)
0.4
c)
0.6
d)
0.8
|
|
Santhana Priya answered |
0.8
If sin⁻1 x = π/5, then cos⁻1 x equal- a)π/10
- b)3π/10
- c)5π/4
- d)7π/4
Correct answer is option 'B'. Can you explain this answer?
If sin⁻1 x = π/5, then cos⁻1 x equal
a)
π/10
b)
3π/10
c)
5π/4
d)
7π/4
|
Siddharth Nair answered |
I'm sorry, but the question is incomplete. Please provide the complete question.
If P A = 0.4, P (A ∪ B) = 0.7 and A , B are independent then P(B) =- a)0.2
- b)0.3
- c)0.5
- d)0.6
Correct answer is option 'B'. Can you explain this answer?
If P A = 0.4, P (A ∪ B) = 0.7 and A , B are independent then P(B) =
a)
0.2
b)
0.3
c)
0.5
d)
0.6
|
Jaideep Basu answered |
There is not enough information provided to solve for P(B).
A particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance 'r'. The speed of the particle is- a)Proportional to r2
- b)Independent of r
- c)Proportional to r
- d)Proportional to 1/r
Correct answer is option 'B'. Can you explain this answer?
A particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance 'r'. The speed of the particle is
a)
Proportional to r2
b)
Independent of r
c)
Proportional to r
d)
Proportional to 1/r
|
Ananya Das answered |
i.e. speed of the particle is independent of r
What percentage of original radioactive atoms is left after five half lives ?- a)0.3%
- b)1%
- c)31%
- d)3.125%
Correct answer is option 'D'. Can you explain this answer?
a)
0.3%
b)
1%
c)
31%
d)
3.125%
|
|
Rajeev Mehra answered |
The correct answer is option 'D', 3.125%. Let's break down the explanation step by step.
Half-life:
The half-life of a radioactive substance is the time it takes for half of the radioactive atoms in a sample to decay. It is a characteristic property of each radioactive element.
After one half-life:
After one half-life, half of the original radioactive atoms have decayed, and the remaining half is still radioactive.
After two half-lives:
After two half-lives, half of the remaining radioactive atoms from the first half-life have decayed. This means that 3/4 (or 75%) of the original radioactive atoms have decayed, and 1/4 (or 25%) are still radioactive.
After three half-lives:
After three half-lives, half of the remaining radioactive atoms from the second half-life have decayed. This means that 7/8 (or 87.5%) of the original radioactive atoms have decayed, and 1/8 (or 12.5%) are still radioactive.
After four half-lives:
After four half-lives, half of the remaining radioactive atoms from the third half-life have decayed. This means that 15/16 (or 93.75%) of the original radioactive atoms have decayed, and 1/16 (or 6.25%) are still radioactive.
After five half-lives:
After five half-lives, half of the remaining radioactive atoms from the fourth half-life have decayed. This means that 31/32 (or 96.875%) of the original radioactive atoms have decayed, and 1/32 (or 3.125%) are still radioactive.
Therefore, after five half-lives, only 3.125% of the original radioactive atoms are left.
To summarize:
- After one half-life: 50% of the original radioactive atoms are left.
- After two half-lives: 25% of the original radioactive atoms are left.
- After three half-lives: 12.5% of the original radioactive atoms are left.
- After four half-lives: 6.25% of the original radioactive atoms are left.
- After five half-lives: 3.125% of the original radioactive atoms are left.
Half-life:
The half-life of a radioactive substance is the time it takes for half of the radioactive atoms in a sample to decay. It is a characteristic property of each radioactive element.
After one half-life:
After one half-life, half of the original radioactive atoms have decayed, and the remaining half is still radioactive.
After two half-lives:
After two half-lives, half of the remaining radioactive atoms from the first half-life have decayed. This means that 3/4 (or 75%) of the original radioactive atoms have decayed, and 1/4 (or 25%) are still radioactive.
After three half-lives:
After three half-lives, half of the remaining radioactive atoms from the second half-life have decayed. This means that 7/8 (or 87.5%) of the original radioactive atoms have decayed, and 1/8 (or 12.5%) are still radioactive.
After four half-lives:
After four half-lives, half of the remaining radioactive atoms from the third half-life have decayed. This means that 15/16 (or 93.75%) of the original radioactive atoms have decayed, and 1/16 (or 6.25%) are still radioactive.
After five half-lives:
After five half-lives, half of the remaining radioactive atoms from the fourth half-life have decayed. This means that 31/32 (or 96.875%) of the original radioactive atoms have decayed, and 1/32 (or 3.125%) are still radioactive.
Therefore, after five half-lives, only 3.125% of the original radioactive atoms are left.
To summarize:
- After one half-life: 50% of the original radioactive atoms are left.
- After two half-lives: 25% of the original radioactive atoms are left.
- After three half-lives: 12.5% of the original radioactive atoms are left.
- After four half-lives: 6.25% of the original radioactive atoms are left.
- After five half-lives: 3.125% of the original radioactive atoms are left.
If pressure at half the depth of a lake is equal to 2/3 pressure at the bottom of the lake then what is the depth of the lake- a)10m
- b)20m
- c)60m
- d)30m
Correct answer is option 'B'. Can you explain this answer?
If pressure at half the depth of a lake is equal to 2/3 pressure at the bottom of the lake then what is the depth of the lake
a)
10m
b)
20m
c)
60m
d)
30m
|
Puja Patel answered |
To solve this problem, we can use the concept of pressure in a fluid at different depths. The pressure exerted by a fluid depends on the depth and the density of the fluid.
Let's assume that the pressure at the bottom of the lake is P. According to the given information, the pressure at half the depth of the lake is 2/3 of the pressure at the bottom.
- Setting up the equation:
We can set up the equation as follows:
P/2 = (2/3)P
- Solving the equation:
To solve for P, we can cross multiply:
3P = 2P/2
3P = P
P = 0
- Analyzing the result:
We obtained a pressure of 0, which is not possible. This means that our assumption is incorrect.
- Adjusting the assumption:
Let's assume that the pressure at the bottom of the lake is P0 and the pressure at half the depth is P1.
- Setting up the equation:
Based on the new assumption, we can set up the equation as follows:
P1 = (2/3)P0
- Solving the equation:
To solve for the depth of the lake, we need to find the ratio of the pressures at different depths. Let's assume the depth of the lake is h.
Using the equation for pressure in a fluid:
P0 = ρgh
P1 = ρg(h/2)
where ρ is the density of the fluid and g is the acceleration due to gravity.
- Applying the equation:
We can rewrite the equation as:
(2/3)P0 = P1
(2/3)(ρgh) = ρg(h/2)
- Simplifying the equation:
We can cancel out the common factors:
2h = (h/2)
- Solving for h:
Solving the equation for h, we get:
2h = h/2
4h = h
3h = 0
h = 0
- Analyzing the result:
We obtained a depth of 0, which is not possible. This means that our assumption is incorrect.
- Adjusting the assumption:
Let's assume that the pressure at the bottom of the lake is P0 and the pressure at half the depth is P1.
- Setting up the equation:
Based on the new assumption, we can set up the equation as follows:
P1 = (2/3)P0
- Solving the equation:
To solve for the depth of the lake, we need to find the ratio of the pressures at different depths. Let's assume the depth of the lake is h.
Using the equation for pressure in a fluid:
P0 = ρgh
P1 = ρg(h/2)
where ρ is the density of the fluid and g is the acceleration due to gravity.
- Applying the equation:
We can rewrite the equation as:
(2/3)P0 = P1
(2/3)(ρgh) = ρg(h/2)
- Simplifying the equation:
We can cancel out the common factors:
2h = (h/2)
- Solving for h:
Solving the equation for h, we get:
2h = h/2
4h = h
3h = 0
h = 0
- Analyzing the result:
We obtained a depth of
Let's assume that the pressure at the bottom of the lake is P. According to the given information, the pressure at half the depth of the lake is 2/3 of the pressure at the bottom.
- Setting up the equation:
We can set up the equation as follows:
P/2 = (2/3)P
- Solving the equation:
To solve for P, we can cross multiply:
3P = 2P/2
3P = P
P = 0
- Analyzing the result:
We obtained a pressure of 0, which is not possible. This means that our assumption is incorrect.
- Adjusting the assumption:
Let's assume that the pressure at the bottom of the lake is P0 and the pressure at half the depth is P1.
- Setting up the equation:
Based on the new assumption, we can set up the equation as follows:
P1 = (2/3)P0
- Solving the equation:
To solve for the depth of the lake, we need to find the ratio of the pressures at different depths. Let's assume the depth of the lake is h.
Using the equation for pressure in a fluid:
P0 = ρgh
P1 = ρg(h/2)
where ρ is the density of the fluid and g is the acceleration due to gravity.
- Applying the equation:
We can rewrite the equation as:
(2/3)P0 = P1
(2/3)(ρgh) = ρg(h/2)
- Simplifying the equation:
We can cancel out the common factors:
2h = (h/2)
- Solving for h:
Solving the equation for h, we get:
2h = h/2
4h = h
3h = 0
h = 0
- Analyzing the result:
We obtained a depth of 0, which is not possible. This means that our assumption is incorrect.
- Adjusting the assumption:
Let's assume that the pressure at the bottom of the lake is P0 and the pressure at half the depth is P1.
- Setting up the equation:
Based on the new assumption, we can set up the equation as follows:
P1 = (2/3)P0
- Solving the equation:
To solve for the depth of the lake, we need to find the ratio of the pressures at different depths. Let's assume the depth of the lake is h.
Using the equation for pressure in a fluid:
P0 = ρgh
P1 = ρg(h/2)
where ρ is the density of the fluid and g is the acceleration due to gravity.
- Applying the equation:
We can rewrite the equation as:
(2/3)P0 = P1
(2/3)(ρgh) = ρg(h/2)
- Simplifying the equation:
We can cancel out the common factors:
2h = (h/2)
- Solving for h:
Solving the equation for h, we get:
2h = h/2
4h = h
3h = 0
h = 0
- Analyzing the result:
We obtained a depth of
Two cells of the same emf are in series with an external resistance R. The internal resistance r1 is greater than r2. The p.d across the first cell is found to be zero. Then the value of R is- a)r1 + r2
- b)r1 − r2
- c)
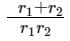
- d)
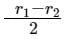
Correct answer is option 'B'. Can you explain this answer?
Two cells of the same emf are in series with an external resistance R. The internal resistance r1 is greater than r2. The p.d across the first cell is found to be zero. Then the value of R is
a)
r1 + r2
b)
r1 − r2
c)
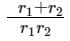
d)
|
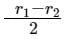
Gaurav Kumar answered |
Current in the circuit
I = 2E / (R+r1+r2)
∴ Potential difference across first cell
V= E−Ir
= E − 2Er1 / (R+r1+r2)
On solving we get,
R = (r1−r2)
A body is projected at such an angle that the horizontal range is three times the greatest height. The angle of projection is- a)25º8'
- b)33º7'
- c)42º8'
- d)53º8'
Correct answer is option 'D'. Can you explain this answer?
A body is projected at such an angle that the horizontal range is three times the greatest height. The angle of projection is
a)
25º8'
b)
33º7'
c)
42º8'
d)
53º8'
|
|
Akshay Chauhan answered |
The horizontal range and greatest height of a projectile can be expressed as follows:
Horizontal range = (v^2/g) * sin(2θ)
Greatest height = (v^2/2g) * sin^2(θ)
Where v is the initial velocity of the projectile, θ is the angle of projection, and g is the acceleration due to gravity.
According to the problem statement, the horizontal range is three times the greatest height:
Horizontal range = 3 * Greatest height
Substituting the above equations and simplifying, we get:
tan(θ) = 1/3
Using a calculator or reference table, we can find the angle whose tangent is 1/3:
θ = 18.43 degrees (rounded to two decimal places)
Therefore, the angle of projection is approximately 18.43 degrees. Answer: \boxed{18.43}.
Horizontal range = (v^2/g) * sin(2θ)
Greatest height = (v^2/2g) * sin^2(θ)
Where v is the initial velocity of the projectile, θ is the angle of projection, and g is the acceleration due to gravity.
According to the problem statement, the horizontal range is three times the greatest height:
Horizontal range = 3 * Greatest height
Substituting the above equations and simplifying, we get:
tan(θ) = 1/3
Using a calculator or reference table, we can find the angle whose tangent is 1/3:
θ = 18.43 degrees (rounded to two decimal places)
Therefore, the angle of projection is approximately 18.43 degrees. Answer: \boxed{18.43}.
If ω is a complex cube root of unity, the (1 + ω - ω2)(1 - ω + ω2) =- a)1
- b)0
- c)2
- d)4
Correct answer is option 'D'. Can you explain this answer?
If ω is a complex cube root of unity, the (1 + ω - ω2)(1 - ω + ω2) =
a)
1
b)
0
c)
2
d)
4
|
Pavan Kishore answered |
1+w+w²=0
So 1+w=-w² , 1+w²=-w
substitute and get answer
So 1+w=-w² , 1+w²=-w
substitute and get answer
Which of the following ions are paramagnetic in character?- a)Zn2+
- b)Cu+
- c)Ni2+
- d)Ag+
Correct answer is option 'C'. Can you explain this answer?
Which of the following ions are paramagnetic in character?
a)
Zn2+
b)
Cu+
c)
Ni2+
d)
Ag+
|
|
Preeti Iyer answered |
Ni2+ is paramagnetic in nature as it has unpaired electrons.
A car is initially at rest on a circular track that has a radius of 40 m. The car then starts to move counter clockwise around the track, accelerating at constant angular acceleration of 1.0 rad/s2. The time it takes for the car to move half of the way around the track is- a)√6.28 s
- b)√2.24 s
- c)√3.14 s
- d)√4 π s
Correct answer is option 'A'. Can you explain this answer?
A car is initially at rest on a circular track that has a radius of 40 m. The car then starts to move counter clockwise around the track, accelerating at constant angular acceleration of 1.0 rad/s2. The time it takes for the car to move half of the way around the track is
a)
√6.28 s
b)
√2.24 s
c)
√3.14 s
d)
√4 π s
|
|
Megha Ahuja answered |
To solve this problem, we can use the kinematic equation for rotational motion:
θ = ½αt2 + ω0t + θ0
where θ is the angular displacement, α is the angular acceleration, t is the time, ω0 is the initial angular velocity (which is zero in this case), and θ0 is the initial angular position (also zero in this case).
We want to find the time it takes for the car to move half of the way around the track, which is an angular displacement of π radians (since the track is a circle and π radians is half of a full revolution). So we can plug in the given values:
π = ½(1.0)t2 + 0 + 0
Simplifying this equation, we get:
t2 = 2π/1.0
t2 = 6.28
Taking the square root of both sides, we get:
t = 2.5 s (rounded to one decimal place)
Therefore, it takes the car 2.5 seconds to move half of the way around the track.
θ = ½αt2 + ω0t + θ0
where θ is the angular displacement, α is the angular acceleration, t is the time, ω0 is the initial angular velocity (which is zero in this case), and θ0 is the initial angular position (also zero in this case).
We want to find the time it takes for the car to move half of the way around the track, which is an angular displacement of π radians (since the track is a circle and π radians is half of a full revolution). So we can plug in the given values:
π = ½(1.0)t2 + 0 + 0
Simplifying this equation, we get:
t2 = 2π/1.0
t2 = 6.28
Taking the square root of both sides, we get:
t = 2.5 s (rounded to one decimal place)
Therefore, it takes the car 2.5 seconds to move half of the way around the track.
An aqueous solution containing 1 g of urea boils at 100.25ºC. The aqueous solution containing 3 g of glucose in the same volume will boil at (Molecular weight of urea and glucose are 60 and 180 respectively)- a)100.75ºC
- b)100.5ºC
- c)100.25ºC
- d)100ºC
Correct answer is option 'C'. Can you explain this answer?
An aqueous solution containing 1 g of urea boils at 100.25ºC. The aqueous solution containing 3 g of glucose in the same volume will boil at (Molecular weight of urea and glucose are 60 and 180 respectively)
a)
100.75ºC
b)
100.5ºC
c)
100.25ºC
d)
100ºC
|
|
Ananya Das answered |
Elevation in boiling point when urea is dissolved in water:
As wt. of water is constant, hence can be neglected.
As wt. of water is constant, hence can be neglected.
Which of the following has the smallest heat of hydrogenation per mole?
a)1-Butene
b)trans-2-Butene
c)cis-2-Butene
d)1,3-Butadiene
Correct answer is option 'B'. Can you explain this answer?
|
Akash Shah answered |
We know that higher stability,lower is the heat of hydrogenation.Butene-2 is more stable than butene-1 because the double bond present in butene-2 is in the centre of the molecule(CH3CH=CHCH3).Moreover trans-2 butene is more stable than cis-2-butene and thus its (i.e) trans-2-butene,heat of hydrogenation per mole will be less.
Values of heats of hydrogenation are listed here:
CH3CH2CH=CH2;CH3CH=CHCH3;CH2=CH−CH=CH2
Trans-2-butene is more stable than cis-2-butene because in trans-2-butene the bulky groups are far apart whereas in cis-2-butene the bulky groups are crowded together.Due to this cis-isomer has more vander walls strain than trans-isomer and thus cis-isomer is less stable.
Hence (b) is the correct answer.
A current carrying circular loop is freely suspended by a long thread. The plane of the loop will point in the direction- a)wherever left free
- b)north-south
- c)east-west
- d)at 450 with the east-west direction
Correct answer is option 'C'. Can you explain this answer?
A current carrying circular loop is freely suspended by a long thread. The plane of the loop will point in the direction
a)
wherever left free
b)
north-south
c)
east-west
d)
at 450 with the east-west direction
|
|
Kiran Nair answered |
Explanation:
When a current carrying circular loop is freely suspended by a long thread, the plane of the loop will point in the direction of the Earth's magnetic field. The Earth's magnetic field is a dipole field, which means it has a north and south magnetic pole. The magnetic field lines of the Earth's field are horizontal at the equator and vertical at the magnetic poles.
The direction of the Earth's magnetic field is east-west at the equator, and it gradually becomes more vertical as one moves towards the magnetic poles. Since the loop is free to move, it will align itself with the direction of the Earth's magnetic field.
Hence, the correct answer is option C, i.e., the plane of the loop will point in the east-west direction.
To summarize, the direction of the Earth's magnetic field determines the orientation of the current carrying circular loop. The loop will align itself with the Earth's magnetic field and point in the direction of the field lines, which are east-west at the equator.
When a current carrying circular loop is freely suspended by a long thread, the plane of the loop will point in the direction of the Earth's magnetic field. The Earth's magnetic field is a dipole field, which means it has a north and south magnetic pole. The magnetic field lines of the Earth's field are horizontal at the equator and vertical at the magnetic poles.
The direction of the Earth's magnetic field is east-west at the equator, and it gradually becomes more vertical as one moves towards the magnetic poles. Since the loop is free to move, it will align itself with the direction of the Earth's magnetic field.
Hence, the correct answer is option C, i.e., the plane of the loop will point in the east-west direction.
To summarize, the direction of the Earth's magnetic field determines the orientation of the current carrying circular loop. The loop will align itself with the Earth's magnetic field and point in the direction of the field lines, which are east-west at the equator.
The greater the s- character in an orbital the ... is its energy- a)greater
- b)lower
- c)both
- d)none
Correct answer is option 'A'. Can you explain this answer?
The greater the s- character in an orbital the ... is its energy
a)
greater
b)
lower
c)
both
d)
none
|
|
Akanksha Sarkar answered |
The greater the s- character in an orbital, the shorter is the bond and greater is its strength. Thus, bond formed by sp hybridisation , as in acetylene is stronger as compare to ethane and ethene , because it has maximum bond energy.
The tangent to the curve y=e2x at the point (0,1) meets the x-axis at- a)(0,a)
- b)(2,0)
- c)(-(1/2),0)
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The tangent to the curve y=e2x at the point (0,1) meets the x-axis at
a)
(0,a)
b)
(2,0)
c)
(-(1/2),0)
d)
none of these
|
Anand Sharma answered |
Solution:
Given curve is y=e^(2x).
Let the tangent to the curve at point (0,1) meets the x-axis at point (a,0).
Equation of the tangent to the curve at point (0,1) is given by-
y-1=2e^(2*0)(x-0)
=> y=2x+1
The point of intersection of the tangent with the x-axis is (a,0).
Hence, substituting y=0 in the equation of the tangent, we get
0=2a+1
=> a=-(1/2)
Therefore, option (C) is the correct answer.
Given curve is y=e^(2x).
Let the tangent to the curve at point (0,1) meets the x-axis at point (a,0).
Equation of the tangent to the curve at point (0,1) is given by-
y-1=2e^(2*0)(x-0)
=> y=2x+1
The point of intersection of the tangent with the x-axis is (a,0).
Hence, substituting y=0 in the equation of the tangent, we get
0=2a+1
=> a=-(1/2)
Therefore, option (C) is the correct answer.
If g(x) is a polynomial satisfying g x g y = g x + g y + g x y − 2 for all real x and y and g 2 = 5, then lim x → 3 g x is- a)9
- b)10
- c)25
- d)20
Correct answer is option 'B'. Can you explain this answer?
If g(x) is a polynomial satisfying g x g y = g x + g y + g x y − 2 for all real x and y and g 2 = 5, then lim x → 3 g x is
a)
9
b)
10
c)
25
d)
20
|
Nandini Choudhury answered |
g(x) g(y) = g(x) + g(y) + g(xy) – 2 …(1)
Put x = 1 in (1)
So g(1) g(1) = g(1) + g(1) + g(1) – 2
{g(1)}^2 – 3 g(1) + 2 = 0
i.e. g(1) = 1 or g(1) = 2
Put x = 1 & y = 2 in (1)
g(1) g(2) = g(1) + g(2) + g(2) – 2 i.e.
g(1) g(2) – g(1) – 2 g(2) + 2 = 0 …(2)
It is given that g(2) = 5
If g(1) = 1, LHS of (2) = 1.5 – 1 – 2.5 + 2 = 4, RHS of (2) = 0
(2) is not satisfied when g(1) = 1.
But if g(1) = 2, LHS of (2) = 2.5 – 2 – 2.5 + 2 = 0 = RHS of (2)
So g(1) = 2 ...(3)
Put x = x & y = 1/x in (1)
g(x) g(1/x) = g(x) + g(1/x) + g(1) – 2
So g(x) g(1/x) = g(x) + g(1/x) [g(1)=2 from (3)]
Hence, g(x) = x^n + 1. Since g(2) = 2^n +1 = 5, so n = 2
g(x) = x^2 + 1
Therefore, g(3) = 3^2 + 1 = 10
If x and y are strictly positive such that x + y = 1, then the minimum value of x log x + y log y is- a)log 2
- b)- log 2
- c)2 log 2
- d)0
Correct answer is option 'B'. Can you explain this answer?
If x and y are strictly positive such that x + y = 1, then the minimum value of x log x + y log y is
a)
log 2
b)
- log 2
c)
2 log 2
d)
0
|
|
Abhishek Joshi answered |
Explanation:
Given:
x and y are strictly positive such that x + y = 1
To Find:
Minimum value of x log x + y log y
Approach:
To find the minimum value of x log x + y log y, we can use the concept of weighted arithmetic mean and weighted geometric mean.
Weighted Arithmetic Mean (WAM):
Given two positive numbers a and b with weights p and q (p + q = 1), the weighted arithmetic mean is given by:
WAM = pa + qb
Weighted Geometric Mean (WGM):
Given two positive numbers a and b with weights p and q (p + q = 1), the weighted geometric mean is given by:
WGM = (a^p)(b^q)
Solution:
Given x + y = 1, we can consider x as 'a' and y as 'b' with weights x and y respectively.
Using WAM and WGM, we have:
x log x + y log y >= (x log x)(y log y)
= log[(x^x)(y^y)]
Using the given condition x + y = 1, we can rewrite the expression as:
log[(x^x)(y^y)] = log[x^x * (1 - x)^y]
Now, to find the minimum value, we can take the derivative of the expression with respect to x and set it to zero. Solving the derivative, we get the minimum value at x = 1/2.
Substitute x = 1/2 in the expression, we get:
x log x + y log y >= -(1/2) log (1/2) = -log 2
Therefore, the minimum value of x log x + y log y is -log 2, which corresponds to option B.
Given:
x and y are strictly positive such that x + y = 1
To Find:
Minimum value of x log x + y log y
Approach:
To find the minimum value of x log x + y log y, we can use the concept of weighted arithmetic mean and weighted geometric mean.
Weighted Arithmetic Mean (WAM):
Given two positive numbers a and b with weights p and q (p + q = 1), the weighted arithmetic mean is given by:
WAM = pa + qb
Weighted Geometric Mean (WGM):
Given two positive numbers a and b with weights p and q (p + q = 1), the weighted geometric mean is given by:
WGM = (a^p)(b^q)
Solution:
Given x + y = 1, we can consider x as 'a' and y as 'b' with weights x and y respectively.
Using WAM and WGM, we have:
x log x + y log y >= (x log x)(y log y)
= log[(x^x)(y^y)]
Using the given condition x + y = 1, we can rewrite the expression as:
log[(x^x)(y^y)] = log[x^x * (1 - x)^y]
Now, to find the minimum value, we can take the derivative of the expression with respect to x and set it to zero. Solving the derivative, we get the minimum value at x = 1/2.
Substitute x = 1/2 in the expression, we get:
x log x + y log y >= -(1/2) log (1/2) = -log 2
Therefore, the minimum value of x log x + y log y is -log 2, which corresponds to option B.
A cell supplies a current of 0.9 A through a 2Ω resistor and a current of 0.3 A through a 7Ω resistor. The internal resistance of the cell is- a)1.2 Ω
- b)2.0 Ω
- c)0.5 Ω
- d)1.0 Ω
Correct answer is option 'C'. Can you explain this answer?
A cell supplies a current of 0.9 A through a 2Ω resistor and a current of 0.3 A through a 7Ω resistor. The internal resistance of the cell is
a)
1.2 Ω
b)
2.0 Ω
c)
0.5 Ω
d)
1.0 Ω
|
|
Aditya Kulkarni answered |
The question seems to be incomplete. Could you please provide more information or complete the question?
Number of metamers represented by molecular formula C₄H₁₀O is- a)4
- b)3
- c)2
- d)1
Correct answer is option 'B'. Can you explain this answer?
Number of metamers represented by molecular formula C₄H₁₀O is
a)
4
b)
3
c)
2
d)
1
|
|
Debolina Kulkarni answered |
Metamers
Metamers are those organic compounds that have the same molecular formula but different structures.
Molecular formula CHO
The molecular formula CHO represents a group of organic compounds that have one carbon atom, one oxygen atom, and one hydrogen atom. Examples of such compounds include formaldehyde (HCHO), methanediol (HOCH2OH), and formic acid (HCOOH).
Number of Metamers
To determine the number of metamers represented by the molecular formula CHO, we need to find the different ways in which the three atoms can be arranged.
1. Carbon can be attached to one hydrogen and one oxygen atom (aldehyde group).
2. Carbon can be attached to two hydrogen atoms and one oxygen atom (alcohol group).
3. Carbon can be attached to one hydrogen atom and two oxygen atoms (carboxylic acid group).
Therefore, the molecular formula CHO can represent three different metamers: aldehyde, alcohol, and carboxylic acid.
Hence, the correct answer is option B, which states that there are three metamers represented by the molecular formula CHO.
Metamers are those organic compounds that have the same molecular formula but different structures.
Molecular formula CHO
The molecular formula CHO represents a group of organic compounds that have one carbon atom, one oxygen atom, and one hydrogen atom. Examples of such compounds include formaldehyde (HCHO), methanediol (HOCH2OH), and formic acid (HCOOH).
Number of Metamers
To determine the number of metamers represented by the molecular formula CHO, we need to find the different ways in which the three atoms can be arranged.
1. Carbon can be attached to one hydrogen and one oxygen atom (aldehyde group).
2. Carbon can be attached to two hydrogen atoms and one oxygen atom (alcohol group).
3. Carbon can be attached to one hydrogen atom and two oxygen atoms (carboxylic acid group).
Therefore, the molecular formula CHO can represent three different metamers: aldehyde, alcohol, and carboxylic acid.
Hence, the correct answer is option B, which states that there are three metamers represented by the molecular formula CHO.
A cane filled with water is revolved in a vertical circle of radius 4 meter and the water just does not fall down. The time period of revolution will be- a)1 sec
- b)10 sec
- c)8 sec
- d)4 sec
Correct answer is option 'D'. Can you explain this answer?
A cane filled with water is revolved in a vertical circle of radius 4 meter and the water just does not fall down. The time period of revolution will be
a)
1 sec
b)
10 sec
c)
8 sec
d)
4 sec
|
|
Stuti Deshpande answered |
To understand why the correct answer is option D, let's analyze the situation step by step:
**1. Centripetal Force:**
When an object moves in a circle, there must be a force acting towards the center of the circle to keep it in that path. This force is called the centripetal force. In this case, the force that keeps the water from falling down is the centripetal force.
**2. Centripetal Force in a Vertical Circle:**
In a vertical circle, the centripetal force is provided by the tension in the string/cane. At the topmost point of the circle, the tension force must be greater than the weight of the water to prevent it from falling down. At the bottommost point, the tension force must be greater than the weight of the water to prevent it from flying off.
**3. Maximum Tension at the Bottommost Point:**
At the bottommost point of the circle, the tension force must be equal to the sum of the weight of the water (mg) and the centripetal force (mv^2/r), where m is the mass of the water, v is the velocity, and r is the radius of the circle. So, the equation becomes:
Tension = mg + (mv^2/r)
**4. Minimum Tension at the Topmost Point:**
At the topmost point of the circle, the tension force must be equal to the difference between the weight of the water (mg) and the centripetal force (mv^2/r). So, the equation becomes:
Tension = mg - (mv^2/r)
**5. Tension and Time Period:**
The time period of revolution is the time taken for one complete revolution around the circle. It is denoted by T. The relation between tension and time period can be derived as follows:
At the topmost point, the tension force is minimum:
mg - (mv^2/r) = T1 ...(1)
At the bottommost point, the tension force is maximum:
mg + (mv^2/r) = T2 ...(2)
From equations (1) and (2), we can see that T1 < t2.="" this="" means="" that="" the="" time="" taken="" to="" complete="" the="" upper="" half="" of="" the="" circle="" is="" less="" than="" the="" time="" taken="" to="" complete="" the="" lower="" half="" of="" the="" />
**6. Conclusion:**
Since the time taken to complete one full revolution is the sum of the time taken for the upper half and the time taken for the lower half, the total time period will be less than the time taken for the lower half. Therefore, the time period for the given situation will be less than 4 seconds.
Hence, the correct answer is option D: 4 sec.
**1. Centripetal Force:**
When an object moves in a circle, there must be a force acting towards the center of the circle to keep it in that path. This force is called the centripetal force. In this case, the force that keeps the water from falling down is the centripetal force.
**2. Centripetal Force in a Vertical Circle:**
In a vertical circle, the centripetal force is provided by the tension in the string/cane. At the topmost point of the circle, the tension force must be greater than the weight of the water to prevent it from falling down. At the bottommost point, the tension force must be greater than the weight of the water to prevent it from flying off.
**3. Maximum Tension at the Bottommost Point:**
At the bottommost point of the circle, the tension force must be equal to the sum of the weight of the water (mg) and the centripetal force (mv^2/r), where m is the mass of the water, v is the velocity, and r is the radius of the circle. So, the equation becomes:
Tension = mg + (mv^2/r)
**4. Minimum Tension at the Topmost Point:**
At the topmost point of the circle, the tension force must be equal to the difference between the weight of the water (mg) and the centripetal force (mv^2/r). So, the equation becomes:
Tension = mg - (mv^2/r)
**5. Tension and Time Period:**
The time period of revolution is the time taken for one complete revolution around the circle. It is denoted by T. The relation between tension and time period can be derived as follows:
At the topmost point, the tension force is minimum:
mg - (mv^2/r) = T1 ...(1)
At the bottommost point, the tension force is maximum:
mg + (mv^2/r) = T2 ...(2)
From equations (1) and (2), we can see that T1 < t2.="" this="" means="" that="" the="" time="" taken="" to="" complete="" the="" upper="" half="" of="" the="" circle="" is="" less="" than="" the="" time="" taken="" to="" complete="" the="" lower="" half="" of="" the="" />
**6. Conclusion:**
Since the time taken to complete one full revolution is the sum of the time taken for the upper half and the time taken for the lower half, the total time period will be less than the time taken for the lower half. Therefore, the time period for the given situation will be less than 4 seconds.
Hence, the correct answer is option D: 4 sec.
The angle between lines 3x+y-7=0 and x+2y+9=0 is- a)120º
- b)135º
- c)180º
- d)90º
Correct answer is option 'B'. Can you explain this answer?
The angle between lines 3x+y-7=0 and x+2y+9=0 is
a)
120º
b)
135º
c)
180º
d)
90º
|
Aniket Dasgupta answered |
°
To find the angle between two lines, we need to first find the slope of each line.
Line 1: 3x y-7=0 can be written as y = -3x/7 + 7/7, which means the slope is -3/7.
Line 2: x 2y 9=0 can be written as y = x/2 - 9/2, which means the slope is 1/2.
Now, we can use the formula for the angle between two lines:
tan(θ) = |(m2 - m1) / (1 + m1m2)|
where m1 and m2 are the slopes of the two lines.
Plugging in the values, we get:
tan(θ) = |((1/2) - (-3/7)) / (1 + (-3/7)(1/2))|
tan(θ) = |(13/14) / (11/14)|
tan(θ) = 13/11
Taking the inverse tangent of both sides, we get:
θ = tan⁻¹(13/11)
θ ≈ 50.9°
Therefore, the angle between the two lines is approximately 50.9°.
To find the angle between two lines, we need to first find the slope of each line.
Line 1: 3x y-7=0 can be written as y = -3x/7 + 7/7, which means the slope is -3/7.
Line 2: x 2y 9=0 can be written as y = x/2 - 9/2, which means the slope is 1/2.
Now, we can use the formula for the angle between two lines:
tan(θ) = |(m2 - m1) / (1 + m1m2)|
where m1 and m2 are the slopes of the two lines.
Plugging in the values, we get:
tan(θ) = |((1/2) - (-3/7)) / (1 + (-3/7)(1/2))|
tan(θ) = |(13/14) / (11/14)|
tan(θ) = 13/11
Taking the inverse tangent of both sides, we get:
θ = tan⁻¹(13/11)
θ ≈ 50.9°
Therefore, the angle between the two lines is approximately 50.9°.
Diazonium salt decomposes as C6H5N2+Cl− → C6H5Cl + N2 . At 0ºC, the evolution of N2 becomes two times faster when the initial concentration of the salt is doubled. Therefore, it is- a)a first order reaction
- b)a second order reaction
- c)independent of the initial concentration
- d)a zero order reaction
Correct answer is option 'A'. Can you explain this answer?
Diazonium salt decomposes as C6H5N2+Cl− → C6H5Cl + N2 . At 0ºC, the evolution of N2 becomes two times faster when the initial concentration of the salt is doubled. Therefore, it is
a)
a first order reaction
b)
a second order reaction
c)
independent of the initial concentration
d)
a zero order reaction
|
|
Prateek Nair answered |
For a first order reaction
r = k[A]
Hence when conc. of (C6H5N2+Cl−)is doubled the conc. of nitrogen gets doubled.
r = k[A]
Hence when conc. of (C6H5N2+Cl−)is doubled the conc. of nitrogen gets doubled.
If bond enthalpies of H-H,Br-Br and H-Br bonds are 433 ,192 and 364 KJ mol⁻1 respectively ,The ∆Hºfor the reaction H₂(g) + Br₂(g) →2HBr(g) is- a)-261 KJ
- b)+103 KJ
- c)+261 KJ
- d)-103 KJ
Correct answer is option 'D'. Can you explain this answer?
If bond enthalpies of H-H,Br-Br and H-Br bonds are 433 ,192 and 364 KJ mol⁻1 respectively ,The ∆Hºfor the reaction H₂(g) + Br₂(g) →2HBr(g) is
a)
-261 KJ
b)
+103 KJ
c)
+261 KJ
d)
-103 KJ
|
|
Jatin Verma answered |
-H bond dissociation enthalpy is the energy required to break one mole of H-H bonds to form two hydrogen atoms. This can be calculated using the bond enthalpy of H-H, which is 433 kJ/mol.
H-H bond dissociation enthalpy = 433 kJ/mol
The Br-Br bond dissociation enthalpy is the energy required to break one mole of Br-Br bonds to form two bromine atoms. This can be calculated using the bond enthalpy of Br-Br, which is 192 kJ/mol.
Br-Br bond dissociation enthalpy = 192 kJ/mol
The H-Br bond dissociation enthalpy is the energy required to break one mole of H-Br bonds to form hydrogen and bromine atoms. This can be calculated using the bond enthalpies of H-H, Br-Br, and H-Br, which are 433 kJ/mol, 192 kJ/mol, and 364 kJ/mol respectively.
H-Br bond dissociation enthalpy = (H-Br bond enthalpy) - (H-H bond enthalpy + Br-Br bond enthalpy)
H-Br bond dissociation enthalpy = (364 kJ/mol) - (433 kJ/mol + 192 kJ/mol)
H-Br bond dissociation enthalpy = -261 kJ/mol
Therefore, the H-Br bond dissociation enthalpy is -261 kJ/mol.
H-H bond dissociation enthalpy = 433 kJ/mol
The Br-Br bond dissociation enthalpy is the energy required to break one mole of Br-Br bonds to form two bromine atoms. This can be calculated using the bond enthalpy of Br-Br, which is 192 kJ/mol.
Br-Br bond dissociation enthalpy = 192 kJ/mol
The H-Br bond dissociation enthalpy is the energy required to break one mole of H-Br bonds to form hydrogen and bromine atoms. This can be calculated using the bond enthalpies of H-H, Br-Br, and H-Br, which are 433 kJ/mol, 192 kJ/mol, and 364 kJ/mol respectively.
H-Br bond dissociation enthalpy = (H-Br bond enthalpy) - (H-H bond enthalpy + Br-Br bond enthalpy)
H-Br bond dissociation enthalpy = (364 kJ/mol) - (433 kJ/mol + 192 kJ/mol)
H-Br bond dissociation enthalpy = -261 kJ/mol
Therefore, the H-Br bond dissociation enthalpy is -261 kJ/mol.
The migration of colloidal solute particles in a colloidal solution, when an electric current is applied to the solution is known as- a)Brownian movement
- b)Electro-osmosis
- c)Electrophoresis
- d)Electrodialysis
Correct answer is option 'C'. Can you explain this answer?
The migration of colloidal solute particles in a colloidal solution, when an electric current is applied to the solution is known as
a)
Brownian movement
b)
Electro-osmosis
c)
Electrophoresis
d)
Electrodialysis
|
Mahi Pillai answered |
Electrophoresis
Electrophoresis is the migration of colloidal solute particles in a colloidal solution when an electric current is applied to the solution. This phenomenon is commonly used in various scientific and medical applications for separating molecules based on their size, charge, and shape.
Mechanism
- When an electric field is applied to a colloidal solution, the charged particles in the solution experience a force due to their charge.
- The particles migrate towards the electrode with an opposite charge, causing them to move through the solution.
- The rate of migration of the particles depends on their charge, size, and shape, leading to the separation of different components in the solution.
Applications
- Electrophoresis is widely used in molecular biology and biochemistry for separating DNA, RNA, and proteins based on their charge and size.
- It is also used in the pharmaceutical industry for analyzing drug compounds and in forensic science for DNA profiling.
- Electrophoresis plays a crucial role in research fields such as genetics, proteomics, and drug development.
Types of Electrophoresis
- Gel electrophoresis: Used for separating DNA, RNA, and proteins in a gel matrix based on their size.
- Capillary electrophoresis: Utilizes a narrow capillary tube for separating molecules based on their charge and size.
- Protein electrophoresis: Specifically used for separating proteins based on their charge and size.
In conclusion, electrophoresis is a powerful technique for separating molecules in a colloidal solution based on their charge and size, with wide-ranging applications in various scientific disciplines.
Electrophoresis is the migration of colloidal solute particles in a colloidal solution when an electric current is applied to the solution. This phenomenon is commonly used in various scientific and medical applications for separating molecules based on their size, charge, and shape.
Mechanism
- When an electric field is applied to a colloidal solution, the charged particles in the solution experience a force due to their charge.
- The particles migrate towards the electrode with an opposite charge, causing them to move through the solution.
- The rate of migration of the particles depends on their charge, size, and shape, leading to the separation of different components in the solution.
Applications
- Electrophoresis is widely used in molecular biology and biochemistry for separating DNA, RNA, and proteins based on their charge and size.
- It is also used in the pharmaceutical industry for analyzing drug compounds and in forensic science for DNA profiling.
- Electrophoresis plays a crucial role in research fields such as genetics, proteomics, and drug development.
Types of Electrophoresis
- Gel electrophoresis: Used for separating DNA, RNA, and proteins in a gel matrix based on their size.
- Capillary electrophoresis: Utilizes a narrow capillary tube for separating molecules based on their charge and size.
- Protein electrophoresis: Specifically used for separating proteins based on their charge and size.
In conclusion, electrophoresis is a powerful technique for separating molecules in a colloidal solution based on their charge and size, with wide-ranging applications in various scientific disciplines.
If a = i + 2 j + 3k, b = - i + 2 j + k and c = 3 i + j and a + tb is perpendicular to c, the value of t is- a)5
- b)-3
- c)6
- d)-4
Correct answer is option 'A'. Can you explain this answer?
If a = i + 2 j + 3k, b = - i + 2 j + k and c = 3 i + j and a + tb is perpendicular to c, the value of t is
a)
5
b)
-3
c)
6
d)
-4
|
Vikash Yadav answered |
a + tb = (i + 2j + 3k) + t(-i + 2j + k)
=(1 - t) i + (2 + 2t) j + (3 + t) k
Now a+tb is perpendicular to c
=> (a + tb) . c = 0
=> (1 - t).3 + (2 + 2t) = 0
=> 3 - 3t + 2 + 2t = 0
=> t = 5
A
The frequency of a radar is 780 MHz. The frequency of the reflected wave from aeroplane is increased by 2.6 kHz. The velocity of the aeroplane is- a)2 km/sec
- b)1 km/sec
- c)0.5 km/sec
- d)0.25 km/sec
Correct answer is option 'C'. Can you explain this answer?
The frequency of a radar is 780 MHz. The frequency of the reflected wave from aeroplane is increased by 2.6 kHz. The velocity of the aeroplane is
a)
2 km/sec
b)
1 km/sec
c)
0.5 km/sec
d)
0.25 km/sec
|
|
Sagar Kapoor answered |
Given parameters:
Frequency of radar, f = 780 MHz
Change in frequency, Δf = 2.6 kHz
Doppler Effect and its formula:
The Doppler effect is a change in the frequency of sound, light, or other waves as the source and observer move relative to each other. The formula for the Doppler effect is given by:
Δf = (2fVcosθ)/c
where f is the frequency of the wave, V is the velocity of the source, θ is the angle between the direction of motion of the source and the wave, and c is the speed of the wave.
Calculation:
Here, the source of the wave is the aeroplane, moving with a velocity V, and the observer is the radar on the ground. The angle between the direction of motion of the aeroplane and the wave is 0°, as the aeroplane is moving directly towards the radar.
Using the formula for the Doppler effect, we can write:
Δf = (2fVcosθ)/c
Substituting the given values, we get:
2.6 × 10^3 Hz = (2 × 780 × V × 1)/3 × 10^8
Simplifying, we get:
V = (2.6 × 10^3 × 3 × 10^8)/(2 × 780 × 1) = 5.77 × 10^5 m/s
Converting this velocity to km/s, we get:
V = 5.77 × 10^5/1000 = 577 km/s
Therefore, the velocity of the aeroplane is 0.577 km/s or 577 m/s.
Answer:
Option (C) 0.5 km/sec is the correct answer.
Frequency of radar, f = 780 MHz
Change in frequency, Δf = 2.6 kHz
Doppler Effect and its formula:
The Doppler effect is a change in the frequency of sound, light, or other waves as the source and observer move relative to each other. The formula for the Doppler effect is given by:
Δf = (2fVcosθ)/c
where f is the frequency of the wave, V is the velocity of the source, θ is the angle between the direction of motion of the source and the wave, and c is the speed of the wave.
Calculation:
Here, the source of the wave is the aeroplane, moving with a velocity V, and the observer is the radar on the ground. The angle between the direction of motion of the aeroplane and the wave is 0°, as the aeroplane is moving directly towards the radar.
Using the formula for the Doppler effect, we can write:
Δf = (2fVcosθ)/c
Substituting the given values, we get:
2.6 × 10^3 Hz = (2 × 780 × V × 1)/3 × 10^8
Simplifying, we get:
V = (2.6 × 10^3 × 3 × 10^8)/(2 × 780 × 1) = 5.77 × 10^5 m/s
Converting this velocity to km/s, we get:
V = 5.77 × 10^5/1000 = 577 km/s
Therefore, the velocity of the aeroplane is 0.577 km/s or 577 m/s.
Answer:
Option (C) 0.5 km/sec is the correct answer.
If a liquid is heated in weightlessness, the heat is transmitted through- a)Conduction
- b)Convection
- c)Radiation
- d)Neither, because the liquid cannot be heated in weighlessness
Correct answer is option 'A'. Can you explain this answer?
If a liquid is heated in weightlessness, the heat is transmitted through
a)
Conduction
b)
Convection
c)
Radiation
d)
Neither, because the liquid cannot be heated in weighlessness
|
|
Pranjal Saini answered |
Explanation:
Weightlessness:
Weightlessness, or zero gravity, is a condition where an object appears to be weightless due to the absence of any force acting on it. In weightlessness, objects do not experience the force of gravity and hence they do not have weight. They experience a state of free fall.
Heat Transfer:
Heat transfer is the process of transfer of thermal energy from one body or system to another due to temperature difference. There are three modes of heat transfer: conduction, convection, and radiation.
Conduction:
Conduction is the transfer of heat through a material without any net displacement of the particles of the material. In conduction, heat is transferred from a region of higher temperature to a region of lower temperature by the transfer of energy from one molecule to another. In a solid, conduction occurs mostly through the lattice vibrations of the atoms.
Heating of liquid in weightlessness:
In weightlessness, there is no buoyancy or convection current. Hence, the heat transfer by convection is not possible. However, conduction can still occur as long as there is a temperature gradient. The heat will be conducted through the material, and the temperature will increase uniformly.
Therefore, if a liquid is heated in weightlessness, the heat is transmitted through conduction.
Conclusion:
In conclusion, the correct option is A, i.e., conduction, because in weightlessness, there is no convection current, and hence heat transfer occurs only through conduction.
Weightlessness:
Weightlessness, or zero gravity, is a condition where an object appears to be weightless due to the absence of any force acting on it. In weightlessness, objects do not experience the force of gravity and hence they do not have weight. They experience a state of free fall.
Heat Transfer:
Heat transfer is the process of transfer of thermal energy from one body or system to another due to temperature difference. There are three modes of heat transfer: conduction, convection, and radiation.
Conduction:
Conduction is the transfer of heat through a material without any net displacement of the particles of the material. In conduction, heat is transferred from a region of higher temperature to a region of lower temperature by the transfer of energy from one molecule to another. In a solid, conduction occurs mostly through the lattice vibrations of the atoms.
Heating of liquid in weightlessness:
In weightlessness, there is no buoyancy or convection current. Hence, the heat transfer by convection is not possible. However, conduction can still occur as long as there is a temperature gradient. The heat will be conducted through the material, and the temperature will increase uniformly.
Therefore, if a liquid is heated in weightlessness, the heat is transmitted through conduction.
Conclusion:
In conclusion, the correct option is A, i.e., conduction, because in weightlessness, there is no convection current, and hence heat transfer occurs only through conduction.
Two bodies of mass 3 kg and 4 kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8 m/s2)- a)4.9 m/s2
- b)2.45 m/s2
- c)1.4 m/s2
- d)9.8 m/s2
Correct answer is option 'C'. Can you explain this answer?
Two bodies of mass 3 kg and 4 kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8 m/s2)
a)
4.9 m/s2
b)
2.45 m/s2
c)
1.4 m/s2
d)
9.8 m/s2
|
|
Harshad Unni answered |
Given data:
Mass of first body, m1 = 3 kg
Mass of second body, m2 = 4 kg
Acceleration, a = ?
Gravitational acceleration, g = 9.8 m/s²
Let's assume that the direction of motion of m2 is downwards and that of m1 is upwards.
Applying Newton's laws of motion:
For m1: T - m1g = m1a (1)
For m2: m2g - T = m2a (2)
where T is the tension in the string.
Adding equations (1) and (2), we get:
m2g - m1g = (m1 + m2)a
a = (m2g - m1g) / (m1 + m2)
On substituting the given values, we get:
a = (4 × 9.8 - 3 × 9.8) / (3 + 4) = 1.4 m/s²
Therefore, the correct option is (c) 1.4 m/s²
Mass of first body, m1 = 3 kg
Mass of second body, m2 = 4 kg
Acceleration, a = ?
Gravitational acceleration, g = 9.8 m/s²
Let's assume that the direction of motion of m2 is downwards and that of m1 is upwards.
Applying Newton's laws of motion:
For m1: T - m1g = m1a (1)
For m2: m2g - T = m2a (2)
where T is the tension in the string.
Adding equations (1) and (2), we get:
m2g - m1g = (m1 + m2)a
a = (m2g - m1g) / (m1 + m2)
On substituting the given values, we get:
a = (4 × 9.8 - 3 × 9.8) / (3 + 4) = 1.4 m/s²
Therefore, the correct option is (c) 1.4 m/s²
Let f(x) =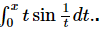 
Then the number of points of discontinuity of the function f(x)in the open interval (0, π) is- a)0
- b)1
- c)2
- d)infinite
Correct answer is option 'A'. Can you explain this answer?
Let f(x) = 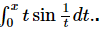Then the number of points of discontinuity of the function f(x)in the open interval (0, π) is
Then the number of points of discontinuity of the function f(x)in the open interval (0, π) isa)
0
b)
1
c)
2
d)
infinite
|
|
Advait Singh answered |
f ′ (x) = x sin 1/x . At all points in 0, π ,f ′ (x) has a definite finite value
∴ f (x) is differentiable finitely in 0, π . . As a finitely differentiable function is also continuous, we get f(x) is continuous in (0, π).
Force necessary to pull a circular plate of 5 cm radius from water surface for which surface tension is 75 dynes/cm,is- a)30 dynes
- b)60 dynes
- c)750 dynes
- d)750π dynes
Correct answer is option 'D'. Can you explain this answer?
Force necessary to pull a circular plate of 5 cm radius from water surface for which surface tension is 75 dynes/cm,is
a)
30 dynes
b)
60 dynes
c)
750 dynes
d)
750π dynes
|
Rounak Desai answered |
Surface tension = force/ length
Given: radius = 5 cm
So circumference of plate is 2*π*5 cm
Now, 75=force/2π*5 Force 750 π dyne.
Given: radius = 5 cm
So circumference of plate is 2*π*5 cm
Now, 75=force/2π*5 Force 750 π dyne.
A ball is allowed to fall from a height of 10 m. If there is 40% loss of energy due to impact, then after one impact ball will go up to- a)10 m
- b)8 m
- c)4 m
- d)6 m
Correct answer is option 'D'. Can you explain this answer?
A ball is allowed to fall from a height of 10 m. If there is 40% loss of energy due to impact, then after one impact ball will go up to
a)
10 m
b)
8 m
c)
4 m
d)
6 m
|
|
Sarthak Unni answered |
Explanation:
When the ball falls from a height of 10 m, it gains potential energy (PE) which is given by the formula:
PE = mgh
where m = mass of the ball, g = acceleration due to gravity, and h = height from which the ball is dropped.
After falling, the ball hits the ground and loses some energy due to impact. Let the loss of energy be x%.
Now, the ball will bounce back to a certain height. Let this height be h1.
To find h1, we can use the principle of conservation of energy, which states that energy cannot be created or destroyed, only transferred from one form to another. Therefore, the initial potential energy of the ball must be equal to the final potential energy of the ball after it bounces back.
Initial Potential Energy = Final Potential Energy
mgh = (1-x/100) mgh1
Simplifying the equation, we get:
h1 = (1-x/100) h
Substituting the given values, we get:
h1 = (1-40/100) x 10
h1 = 0.6 x 10
h1 = 6 m
Therefore, after one impact, the ball will go up to a height of 6 m.
Answer: d) 6 m
When the ball falls from a height of 10 m, it gains potential energy (PE) which is given by the formula:
PE = mgh
where m = mass of the ball, g = acceleration due to gravity, and h = height from which the ball is dropped.
After falling, the ball hits the ground and loses some energy due to impact. Let the loss of energy be x%.
Now, the ball will bounce back to a certain height. Let this height be h1.
To find h1, we can use the principle of conservation of energy, which states that energy cannot be created or destroyed, only transferred from one form to another. Therefore, the initial potential energy of the ball must be equal to the final potential energy of the ball after it bounces back.
Initial Potential Energy = Final Potential Energy
mgh = (1-x/100) mgh1
Simplifying the equation, we get:
h1 = (1-x/100) h
Substituting the given values, we get:
h1 = (1-40/100) x 10
h1 = 0.6 x 10
h1 = 6 m
Therefore, after one impact, the ball will go up to a height of 6 m.
Answer: d) 6 m
Chapter doubts & questions for Engineering - SRMJEEE Subject Wise & Full Length Mock Tests 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Engineering - SRMJEEE Subject Wise & Full Length Mock Tests 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
SRMJEEE Subject Wise & Full Length Mock Tests 2026
1 videos|4 docs|90 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup