All Exams >
GMAT >
Daily Tests for GMAT Preparation >
All Questions
All questions of Day 32 for GMAT Exam
In Jonathan’s pen there are 300 sheep’s. 5/6 of the sheep’s are white, 2/3 of the sheep’s have soft wool. What can’t be the number of white sheep’s that also have soft wool in the pen?a) 150b) 200c) 190d) 180e) 160Correct answer is option 'A'. Can you explain this answer?
|
Yeshwanth Varma answered |
Answer can't be 200, it can be 150 but not 200
There are 40 students in a classroom, 9/20 of them are boys and 4/5 of them are right-handed. How many right-handed boys are there in the classroom?- a)Between 10 and 32.
- b)Between 14 and 32.
- c)Between 10 and 18.
- d)Between 14 and 18.
- e)Between 18 and 36
Correct answer is option 'C'. Can you explain this answer?
There are 40 students in a classroom, 9/20 of them are boys and 4/5 of them are right-handed. How many right-handed boys are there in the classroom?
a)
Between 10 and 32.
b)
Between 14 and 32.
c)
Between 10 and 18.
d)
Between 14 and 18.
e)
Between 18 and 36
|
Meera Rana answered |
Given that there are 18 boys (9/20*40=18) and 22 girls in the class. Also we know that out of 40 students 32 are right-handed (4/5*40=32).
Maximum number of right-handed boys possible is if ALL 18 boys are right-handed;
Minimum number of right-handed boys possible is if ALL 22 girls are right-handed, so in this case 32-22=10 boys would be right-handed.
Maximum number of right-handed boys possible is if ALL 18 boys are right-handed;
Minimum number of right-handed boys possible is if ALL 22 girls are right-handed, so in this case 32-22=10 boys would be right-handed.
There are 200 cats in Cat-City. Out of the 200, 70 are street cats and the rest are domestic cats. 110 cats are gray, 30 out of the gray cats are street ones. How many domestic cats are there which are not gray in Cat-City?
a) 90b) 80c) 50d) 40e) 25Correct answer is option 'C'. Can you explain this answer?
|
Devansh Shah answered |
Out of 200 cats, 130 are domestic ones. Out of 110 gray cats, 30 are street cats therefore 80 are grey and domestic ones.
Altogether there are 130 domestic cats, 80 are grey so (130 – 80) = 50 are not grey.
Altogether there are 130 domestic cats, 80 are grey so (130 – 80) = 50 are not grey.
If A2 + B2 = 15 and AB = 10, what is the value of the expression (A – B)2 + (A + B)2 ?- a)10
- b)20
- c)30
- d)60
- e)70
Correct answer is option 'C'. Can you explain this answer?
If A2 + B2 = 15 and AB = 10, what is the value of the expression (A – B)2 + (A + B)2 ?
a)
10
b)
20
c)
30
d)
60
e)
70
|
Kirti Roy answered |
The best answer is C.
(A – B)2 + (A + B)2 = A2 – 2AB + B2 + A2 + 2AB + B2 = 2(A2 + B2) = 30.
(A – B)2 + (A + B)2 = A2 – 2AB + B2 + A2 + 2AB + B2 = 2(A2 + B2) = 30.
There are 40 students in a classroom, 9/20 of them are boys and 4/5 of them are right-handed. How many right-handed boys are there in the classroom?- a)Between 10 and 32.
- b)Between 14 and 32.
- c)Between 10 and 18.
- d)Between 14 and 18.
- e)Between 18 and 36
Correct answer is option 'C'. Can you explain this answer?
There are 40 students in a classroom, 9/20 of them are boys and 4/5 of them are right-handed. How many right-handed boys are there in the classroom?
a)
Between 10 and 32.
b)
Between 14 and 32.
c)
Between 10 and 18.
d)
Between 14 and 18.
e)
Between 18 and 36
|
|
Sounak Iyer answered |
There are (9/20 x 40 = 18) boys in the class. 80% of them are right-handed, meaning that (4/5 x 18 = 14.4). Answer C is the best answer.
In the Kan film festival, 50 movies were presented. 3/5 of the movies are action movies and 4/5 is science fiction movies. How many of the movies were science fiction action movies?- a)10
- b)15
- c)20
- d)30
- e)35
Correct answer is option 'C'. Can you explain this answer?
In the Kan film festival, 50 movies were presented. 3/5 of the movies are action movies and 4/5 is science fiction movies. How many of the movies were science fiction action movies?
a)
10
b)
15
c)
20
d)
30
e)
35
|
|
Nitya Kumar answered |
There were (3/5 x 50 = 30) action movies.
There were (4/5 x 50 = 40) science fiction movies.
Exact overlapping is calculated by minimum overlapping method.
Therefore there are (40 + 30 – 50 = 20) movies that belong to both categories.
There were (4/5 x 50 = 40) science fiction movies.
Exact overlapping is calculated by minimum overlapping method.
Therefore there are (40 + 30 – 50 = 20) movies that belong to both categories.
A certain airline’s fleet consisted of 60 type A planes at the beginning of 1980. At the end of each year, starting with 1980, the airline retired 3 of the type A planes and acquired 4 new type B planes. How many years did it take before the number of type A planes left in the airline’s fleet was less than 50 percent of the fleet?- a)6
- b)7
- c)8
- d)9
- e)10
Correct answer is option 'D'. Can you explain this answer?
A certain airline’s fleet consisted of 60 type A planes at the beginning of 1980. At the end of each year, starting with 1980, the airline retired 3 of the type A planes and acquired 4 new type B planes. How many years did it take before the number of type A planes left in the airline’s fleet was less than 50 percent of the fleet?
a)
6
b)
7
c)
8
d)
9
e)
10
|
|
Niharika Sen answered |
Understanding the problem:
The airline starts with 60 type A planes and at the end of each year, it retires 3 type A planes and acquires 4 new type B planes.
Calculating the number of type A planes over the years:
- Year 1980: 60 type A planes
- Year 1981: 60 - 3 = 57 type A planes
- Year 1982: 57 - 3 = 54 type A planes
- Year 1983: 54 - 3 = 51 type A planes
- Year 1984: 51 - 3 = 48 type A planes
Finding the answer:
After 5 years (by the end of 1984), the number of type A planes is 48, which is less than 50% of the fleet (60/2 = 30). Therefore, it took 5 years for the number of type A planes left in the airline's fleet to be less than 50%.
Conclusion:
The correct answer is option D - 9 years.
The airline starts with 60 type A planes and at the end of each year, it retires 3 type A planes and acquires 4 new type B planes.
Calculating the number of type A planes over the years:
- Year 1980: 60 type A planes
- Year 1981: 60 - 3 = 57 type A planes
- Year 1982: 57 - 3 = 54 type A planes
- Year 1983: 54 - 3 = 51 type A planes
- Year 1984: 51 - 3 = 48 type A planes
Finding the answer:
After 5 years (by the end of 1984), the number of type A planes is 48, which is less than 50% of the fleet (60/2 = 30). Therefore, it took 5 years for the number of type A planes left in the airline's fleet to be less than 50%.
Conclusion:
The correct answer is option D - 9 years.
Rates for having a manuscript typed at a certain typing service are $5 per page for the first time a page is typed and $3 per page each time a page is revised. If a certain manuscript has 100 pages, of which 40 were revised only once, 10 were revised twice, and the rest required no revisions, what was the total cost of having the manuscript typed?- a)$430
- b)$620
- c)$650
- d)$680
- e)$770
Correct answer is option 'D'. Can you explain this answer?
Rates for having a manuscript typed at a certain typing service are $5 per page for the first time a page is typed and $3 per page each time a page is revised. If a certain manuscript has 100 pages, of which 40 were revised only once, 10 were revised twice, and the rest required no revisions, what was the total cost of having the manuscript typed?
a)
$430
b)
$620
c)
$650
d)
$680
e)
$770
|
|
Palak Saha answered |
Given Information:
- Rate for typing: $5 per page for the first time, $3 per page for revisions
- Total pages in manuscript: 100
- Pages revised once: 40
- Pages revised twice: 10
Calculation:
1. Total cost for typing the 100 pages initially:
$5 x 100 = $500
2. Total cost for revising 40 pages once:
$3 x 40 = $120
3. Total cost for revising 10 pages twice:
$3 x 10 x 2 = $60
Total Cost:
$500 (initial typing) + $120 (1st revision) + $60 (2nd revision) = $680
Therefore, the total cost of having the manuscript typed is $680. Option D is the correct answer.
- Rate for typing: $5 per page for the first time, $3 per page for revisions
- Total pages in manuscript: 100
- Pages revised once: 40
- Pages revised twice: 10
Calculation:
1. Total cost for typing the 100 pages initially:
$5 x 100 = $500
2. Total cost for revising 40 pages once:
$3 x 40 = $120
3. Total cost for revising 10 pages twice:
$3 x 10 x 2 = $60
Total Cost:
$500 (initial typing) + $120 (1st revision) + $60 (2nd revision) = $680
Therefore, the total cost of having the manuscript typed is $680. Option D is the correct answer.
If X ~ Y = X2 + XY, then what is the value of -1 ~ 2 ?- a)1
- b)-1
- c)3
- d)4
- e)2
Correct answer is option 'B'. Can you explain this answer?
If X ~ Y = X2 + XY, then what is the value of -1 ~ 2 ?
a)
1
b)
-1
c)
3
d)
4
e)
2
|
|
Nitya Kumar answered |
The best answer is B.-1 ~ 2 = (-1)2 + (-1)2 = -1.
An Ameba is an organic life form that divides into two Amebas each round hour. If at a certain round hour, two Amebas were placed in a jar, how many Amebas will be in the jar in N hours?- a)2N
- b)22N
- c)2N+1
- d)2N-1
- e)2N
Correct answer is option 'C'. Can you explain this answer?
An Ameba is an organic life form that divides into two Amebas each round hour. If at a certain round hour, two Amebas were placed in a jar, how many Amebas will be in the jar in N hours?
a)
2N
b)
22N
c)
2N+1
d)
2N-1
e)
2N
|
|
Sounak Iyer answered |
Let’s find the number of Amebas in the first hours.
After one hour (N=1) there will be 4 Amebas.
After two hours (N=2) there will be 8 Amebas.
After three hours (N=3) there will be 16 amebas.
Therefore the formula that fits this series is 2N+1.
After one hour (N=1) there will be 4 Amebas.
After two hours (N=2) there will be 8 Amebas.
After three hours (N=3) there will be 16 amebas.
Therefore the formula that fits this series is 2N+1.
The value of an “Aerosoul” stock changes according to the following method:At the end of each month her value is doubled but due to commission the stock’s value is decreases by $10. If the value at the beginning of January is $A, what would be her value at the end of February?- a)4A – 10
- b)4A – 20
- c)4A – 30
- d)4A – 40
- e)4A – 50
Correct answer is option 'C'. Can you explain this answer?
The value of an “Aerosoul” stock changes according to the following method:At the end of each month her value is doubled but due to commission the stock’s value is decreases by $10. If the value at the beginning of January is $A, what would be her value at the end of February?
a)
4A – 10
b)
4A – 20
c)
4A – 30
d)
4A – 40
e)
4A – 50
|
|
Pallavi Sharma answered |
Asset is the worth or estimated worth of that asset. This can be determined through various methods such as market value, book value, or appraisals. The value of an asset can change over time due to factors such as market conditions, demand, and supply. It is important to regularly assess the value of assets to make informed financial decisions and to ensure accurate financial reporting.
Two carpenters, working in the same pace, can build 2 desks in two hours and a half. How many desks can 4 carpenters build in 4 hours?- a)2.4
- b)3.6
- c)4.2
- d)5.5
- e)6.4
Correct answer is option 'E'. Can you explain this answer?
Two carpenters, working in the same pace, can build 2 desks in two hours and a half. How many desks can 4 carpenters build in 4 hours?
a)
2.4
b)
3.6
c)
4.2
d)
5.5
e)
6.4
|
|
Akshay Khanna answered |
2 carpenters build 2 desks in 2.5 hours ---> 4 carpenters build 4 desks in 2.5 hours ----> In 4 hours there are (4/2.5 = 1.6) time units. And (4 x 1.6) is 6.4 desks.
If A and B are positive integers, which of the following expressions is not an integer for certain?- a)(2A2 – 2B2)/(A+B).
- b)(6B + 8A)/(3B + 4A).
- c)(3A – B)/(B - 3A).
- d)(A + B)/(A2 + B2 + 2AB).
- e)(A2 – B2)/(A - B).
Correct answer is option 'D'. Can you explain this answer?
If A and B are positive integers, which of the following expressions is not an integer for certain?
a)
(2A2 – 2B2)/(A+B).
b)
(6B + 8A)/(3B + 4A).
c)
(3A – B)/(B - 3A).
d)
(A + B)/(A2 + B2 + 2AB).
e)
(A2 – B2)/(A - B).
|
|
Bhavana Kulkarni answered |
The best answer is D.
All the answers besides D are numbers after some simplification.Answer D = (A + B)/(A+B)2 = 1/(A+B), and this is a fraction of a number.
All the answers besides D are numbers after some simplification.Answer D = (A + B)/(A+B)2 = 1/(A+B), and this is a fraction of a number.
Alfa, Beta and Gamma are inner angles in a triangle. If Alfa = Beta + Gamma, what can’t be the size of Beta?- a)44 degrees.
- b)45 degrees.
- c)89 degrees.
- d)90 degrees.
- e)There isn’t enough data to determine
Correct answer is option 'D'. Can you explain this answer?
Alfa, Beta and Gamma are inner angles in a triangle. If Alfa = Beta + Gamma, what can’t be the size of Beta?
a)
44 degrees.
b)
45 degrees.
c)
89 degrees.
d)
90 degrees.
e)
There isn’t enough data to determine
|
|
Sharmila Nambiar answered |
If Beta is 90 degrees than Alfa is bigger than 90 and the sum of the angles in the triangle will be bigger than 180 degrees.
15 Java programmers, working in a constant pace, finish a web page in 3 days. If after one day, 9 programmers quit, how many more days are needed to finish the remainder of the job?
- a)5
- b)2
- c)8
- d)4
- e)6
Correct answer is option 'A'. Can you explain this answer?
15 Java programmers, working in a constant pace, finish a web page in 3 days. If after one day, 9 programmers quit, how many more days are needed to finish the remainder of the job?
a)
5
b)
2
c)
8
d)
4
e)
6
|
|
Arjun Iyer answered |
Problem Analysis
Given that 15 Java programmers can finish a web page in 3 days, we need to determine how many more days are needed to finish the remainder of the job after 9 programmers quit after the first day.
Calculation
To calculate the number of days needed to finish the remainder of the job, we can use the concept of person-days.
Initially, we have 15 programmers working for 3 days, which gives us a total of 15 x 3 = 45 person-days of work.
After the first day, 9 programmers quit, so we are left with 15 - 9 = 6 programmers.
The work completed by these 6 programmers in the first day is equivalent to 6 person-days.
Therefore, the work remaining after the first day is 45 - 6 = 39 person-days.
Since we now have 6 programmers working, we can calculate the number of days needed to complete the remaining work.
The number of days required is given by the equation:
(Number of programmers) x (Number of days) = Total person-days of work
Substituting the values, we have:
6 x (Number of days) = 39
Simplifying the equation, we find:
(Number of days) = 39 / 6 = 6.5
Since the number of days must be a whole number, we round up to the nearest whole number.
Therefore, we need 7 more days to finish the remainder of the job.
Conclusion
After 9 programmers quit, 6 programmers are left to complete the remaining work. These 6 programmers will require 7 more days to finish the job.
Therefore, the correct answer is option A) 5.
Given that 15 Java programmers can finish a web page in 3 days, we need to determine how many more days are needed to finish the remainder of the job after 9 programmers quit after the first day.
Calculation
To calculate the number of days needed to finish the remainder of the job, we can use the concept of person-days.
Initially, we have 15 programmers working for 3 days, which gives us a total of 15 x 3 = 45 person-days of work.
After the first day, 9 programmers quit, so we are left with 15 - 9 = 6 programmers.
The work completed by these 6 programmers in the first day is equivalent to 6 person-days.
Therefore, the work remaining after the first day is 45 - 6 = 39 person-days.
Since we now have 6 programmers working, we can calculate the number of days needed to complete the remaining work.
The number of days required is given by the equation:
(Number of programmers) x (Number of days) = Total person-days of work
Substituting the values, we have:
6 x (Number of days) = 39
Simplifying the equation, we find:
(Number of days) = 39 / 6 = 6.5
Since the number of days must be a whole number, we round up to the nearest whole number.
Therefore, we need 7 more days to finish the remainder of the job.
Conclusion
After 9 programmers quit, 6 programmers are left to complete the remaining work. These 6 programmers will require 7 more days to finish the job.
Therefore, the correct answer is option A) 5.
For every X, the action [X] is defined in the following matter: [X] is the greatest integer that is smaller or equal to X. For example: [8.9] = 8.What is the value of [6.5] x [2/3] + [2] x 7.2 + [8.4] – 6.6 ?- a)15.8
- b)16.2
- c)16.4
- d)14.4
- e)12.6
Correct answer is option 'A'. Can you explain this answer?
For every X, the action [X] is defined in the following matter: [X] is the greatest integer that is smaller or equal to X. For example: [8.9] = 8.
What is the value of [6.5] x [2/3] + [2] x 7.2 + [8.4] – 6.6 ?
a)
15.8
b)
16.2
c)
16.4
d)
14.4
e)
12.6
|
|
Jatin Kapoor answered |
The best answer is A.
[6.5] x [2/3] + [2] x 7.2 + [8.4] – 6.6 = 6 x 0 + 2 x 7.2 + 8 - 6.6 = 15.8.
What is the sum of all the even numbers bigger than (-10) and smaller than 12?- a)2
- b)10
- c)0
- d)8
- e)4
Correct answer is option 'B'. Can you explain this answer?
What is the sum of all the even numbers bigger than (-10) and smaller than 12?
a)
2
b)
10
c)
0
d)
8
e)
4
|
|
Aditya Gupta answered |
Sum of Even Numbers
To find the sum of all the even numbers between -10 and 12, we need to identify the even numbers within this range and then add them up.
Identifying Even Numbers
To identify the even numbers, we need to determine the numbers that are divisible by 2. We can start by listing the numbers between -10 and 12:
-10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
From this list, we can see that the even numbers are -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10.
Calculating the Sum
To calculate the sum of these even numbers, we can add them up using basic arithmetic:
-10 + (-8) + (-6) + (-4) + (-2) + 0 + 2 + 4 + 6 + 8 + 10
Simplifying the expression, we get:
-10 - 8 - 6 - 4 - 2 + 0 + 2 + 4 + 6 + 8 + 10
The negative numbers can be rearranged to form a positive sum:
(-10 + 10) + (-8 + 8) + (-6 + 6) + (-4 + 4) + (-2 + 2) + 0 + 2 + 4 + 6 + 8 + 10
This simplifies to:
0 + 0 + 0 + 0 + 0 + 0 + 2 + 4 + 6 + 8 + 10
Finally, adding up all the numbers, we get:
2 + 4 + 6 + 8 + 10 = 30
Therefore, the sum of all the even numbers between -10 and 12 is 30.
Correct Answer: (b) 10
To find the sum of all the even numbers between -10 and 12, we need to identify the even numbers within this range and then add them up.
Identifying Even Numbers
To identify the even numbers, we need to determine the numbers that are divisible by 2. We can start by listing the numbers between -10 and 12:
-10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
From this list, we can see that the even numbers are -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10.
Calculating the Sum
To calculate the sum of these even numbers, we can add them up using basic arithmetic:
-10 + (-8) + (-6) + (-4) + (-2) + 0 + 2 + 4 + 6 + 8 + 10
Simplifying the expression, we get:
-10 - 8 - 6 - 4 - 2 + 0 + 2 + 4 + 6 + 8 + 10
The negative numbers can be rearranged to form a positive sum:
(-10 + 10) + (-8 + 8) + (-6 + 6) + (-4 + 4) + (-2 + 2) + 0 + 2 + 4 + 6 + 8 + 10
This simplifies to:
0 + 0 + 0 + 0 + 0 + 0 + 2 + 4 + 6 + 8 + 10
Finally, adding up all the numbers, we get:
2 + 4 + 6 + 8 + 10 = 30
Therefore, the sum of all the even numbers between -10 and 12 is 30.
Correct Answer: (b) 10
In a psychology school the grade of the students is determined by the following method: At the end of the first year the grade equals to twice the age of the student. From then on, the grade is determined by twice the age of the student plus half of his grade from the previous year. If Joey’s grade at the end of the first year is 40, what will be his grade at the end of the third year?- a)75
- b)62
- c)80
- d)44
- e)56
Correct answer is option 'A'. Can you explain this answer?
In a psychology school the grade of the students is determined by the following method: At the end of the first year the grade equals to twice the age of the student. From then on, the grade is determined by twice the age of the student plus half of his grade from the previous year. If Joey’s grade at the end of the first year is 40, what will be his grade at the end of the third year?
a)
75
b)
62
c)
80
d)
44
e)
56
|
|
Aditya Sharma answered |
Understanding the Grading System
The grading system for students is defined as follows:
- At the end of the first year, the grade is determined by twice the age of the student.
- From the second year onwards, the grade is calculated using the formula:
- Grade = 2 * Age + 0.5 * Previous Grade
Initial Information
For Joey:
- At the end of the first year, his grade is 40.
Calculating Joey's Age
Since Joey's grade at the end of the first year is 40, we can find his age:
- Grade (First Year) = 2 * Age
- 40 = 2 * Age
- Age = 40 / 2 = 20 years old
Calculating the Second Year Grade
Now, to find the grade at the end of the second year, we need Joey's age in the second year:
- Age (Second Year) = 20 + 1 = 21 years old
Using the grading formula:
- Grade (Second Year) = 2 * Age (21) + 0.5 * Previous Grade (40)
- Grade (Second Year) = 2 * 21 + 0.5 * 40
- Grade (Second Year) = 42 + 20 = 62
Calculating the Third Year Grade
Now, to find the grade at the end of the third year:
- Age (Third Year) = 21 + 1 = 22 years old
Using the grading formula again:
- Grade (Third Year) = 2 * Age (22) + 0.5 * Previous Grade (62)
- Grade (Third Year) = 2 * 22 + 0.5 * 62
- Grade (Third Year) = 44 + 31 = 75
Conclusion
Thus, Joey's grade at the end of the third year will be 75, which corresponds to option A.
The grading system for students is defined as follows:
- At the end of the first year, the grade is determined by twice the age of the student.
- From the second year onwards, the grade is calculated using the formula:
- Grade = 2 * Age + 0.5 * Previous Grade
Initial Information
For Joey:
- At the end of the first year, his grade is 40.
Calculating Joey's Age
Since Joey's grade at the end of the first year is 40, we can find his age:
- Grade (First Year) = 2 * Age
- 40 = 2 * Age
- Age = 40 / 2 = 20 years old
Calculating the Second Year Grade
Now, to find the grade at the end of the second year, we need Joey's age in the second year:
- Age (Second Year) = 20 + 1 = 21 years old
Using the grading formula:
- Grade (Second Year) = 2 * Age (21) + 0.5 * Previous Grade (40)
- Grade (Second Year) = 2 * 21 + 0.5 * 40
- Grade (Second Year) = 42 + 20 = 62
Calculating the Third Year Grade
Now, to find the grade at the end of the third year:
- Age (Third Year) = 21 + 1 = 22 years old
Using the grading formula again:
- Grade (Third Year) = 2 * Age (22) + 0.5 * Previous Grade (62)
- Grade (Third Year) = 2 * 22 + 0.5 * 62
- Grade (Third Year) = 44 + 31 = 75
Conclusion
Thus, Joey's grade at the end of the third year will be 75, which corresponds to option A.
Ross has 40 shirts, ¾ of the shirts are green and 1/10 is without buttons.Therefore Ross has between ___ and ___ shirts with buttons that are not green.- a)6 ; 10.
- b)4 ; 25
- c)4 ; 10
- d)5 ; 25
- e)3 ; 10
Correct answer is option 'A'. Can you explain this answer?
Ross has 40 shirts, ¾ of the shirts are green and 1/10 is without buttons.
Therefore Ross has between ___ and ___ shirts with buttons that are not green.
a)
6 ; 10.
b)
4 ; 25
c)
4 ; 10
d)
5 ; 25
e)
3 ; 10
|
|
Nilotpal Sen answered |
Notice that the groups that we are looking for a overlapping are the not-green shirts and the buttoned ones. The not-green shirts are a quarter of 40, 10 shirts.
The shirts with buttons are (9/10 x 40 = 36).
The maximum overlapping is the size of the smallest group: 10.
The minimum overlapping is: 36 + 10 – 40 = 6.
Therefore A is the answer.
The shirts with buttons are (9/10 x 40 = 36).
The maximum overlapping is the size of the smallest group: 10.
The minimum overlapping is: 36 + 10 – 40 = 6.
Therefore A is the answer.
Which of the following fractions is the smallest?- a)3/10
- b)6/19
- c)3/8
- d)11/30
- e)12/31
Correct answer is option 'A'. Can you explain this answer?
Which of the following fractions is the smallest?
a)
3/10
b)
6/19
c)
3/8
d)
11/30
e)
12/31
|
|
Kalyan Nair answered |
The best answer is A
.Compare all of the answers to
(a) 3/10.
(b) 3/10 x 2 = 6/20 which is smaller than 6/19.
(c) 3/10 is smaller.
(d) 3/10 = 9/30, and this is smaller than 11/30.
(e) 3/10 = 12/40 and that is smaller than 12/31.
The smallest fraction is A.
.Compare all of the answers to
(a) 3/10.
(b) 3/10 x 2 = 6/20 which is smaller than 6/19.
(c) 3/10 is smaller.
(d) 3/10 = 9/30, and this is smaller than 11/30.
(e) 3/10 = 12/40 and that is smaller than 12/31.
The smallest fraction is A.
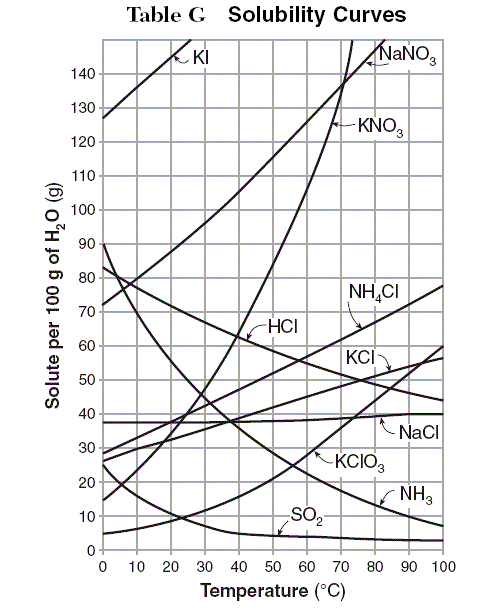The graph shows how the solubility of various chemicals varies with temperature. The solubility is measured as grams of dissolved chemical (solute) per 100 grams of water.
Under the assumption that the curves shown continue in the same general shape beyond the plotted area, use the drop-down menus to complete each of the following statements in the manner that most accurately reflects the information provided.
1. At 60°C, the most soluble of the chemicals is most likely__________.
2. There is most likely a temperature above 100°C at which NH4Cl is exactly as soluble as ___________.- a)1. SO2
2. KCl - b)1. KI
2. KClO3 - c)1. HCl
2. NH3 - d)1. SO2
2. NaCl - e)1. KClO3 2. NaNO3
Correct answer is option 'B'. Can you explain this answer?
The graph shows how the solubility of various chemicals varies with temperature. The solubility is measured as grams of dissolved chemical (solute) per 100 grams of water.
Under the assumption that the curves shown continue in the same general shape beyond the plotted area, use the drop-down menus to complete each of the following statements in the manner that most accurately reflects the information provided.
1. At 60°C, the most soluble of the chemicals is most likely__________.
2. There is most likely a temperature above 100°C at which NH4Cl is exactly as soluble as ___________.
Under the assumption that the curves shown continue in the same general shape beyond the plotted area, use the drop-down menus to complete each of the following statements in the manner that most accurately reflects the information provided.
1. At 60°C, the most soluble of the chemicals is most likely__________.
2. There is most likely a temperature above 100°C at which NH4Cl is exactly as soluble as ___________.
a)
1. SO2
2. KCl
2. KCl
b)
1. KI
2. KClO3
2. KClO3
c)
1. HCl
2. NH3
2. NH3
d)
1. SO2
2. NaCl
2. NaCl
e)
1. KClO3
2. NaNO3
|
EduRev GMAT answered |
By following the gridline at 60°C, the visible line indicating the solubility of NaNO3 is highest on the graph. However, the line for KI extends above the scale shown on the graph. So, given the assumption that the curves continue in the same general shape beyond the plotted area, the information given indicates that KI is the most soluble at 60°C.
The correct answer is KI.
The vertical distance between the solubility curves for KClO3 and NH4Cl decreases as the temperature increases, thus the difference in solubility between KClO3 and NH4Cl decreases as the temperature increases. Assuming that the curves continue in the same general shape beyond the plotted area, the vertical distance between them will eventually be zero, thereby indicating that there is a temperature at which the two chemicals are equally soluble. By contrast, the solubility curves for KCl and NaCl have increasingly greater vertical distances from that of NH4Cl as the temperature increases. Thus the differences in the solubilities of either KCl or NaCl as compared to that of NH4Cl would continue to increase as the temperature increases.
The correct answer is KClO3.
The correct answer is KI.
The vertical distance between the solubility curves for KClO3 and NH4Cl decreases as the temperature increases, thus the difference in solubility between KClO3 and NH4Cl decreases as the temperature increases. Assuming that the curves continue in the same general shape beyond the plotted area, the vertical distance between them will eventually be zero, thereby indicating that there is a temperature at which the two chemicals are equally soluble. By contrast, the solubility curves for KCl and NaCl have increasingly greater vertical distances from that of NH4Cl as the temperature increases. Thus the differences in the solubilities of either KCl or NaCl as compared to that of NH4Cl would continue to increase as the temperature increases.
The correct answer is KClO3.
Each type A machine fills 400 cans per minute,each Type B machine fills 600 cans per minute,and each Type C machine installs 2,400 lids per minute.A lid is installed on each can that is filled and on no can that is not filled.For a particular minute,what is the total number of machines working?(1) A total of 4,800 cans are filled that minute
(2) For that minute,there are 2 Type B machines working for every Type C machine working- a)Statement 1 alone is sufficient, but Statement 2 alone is not.
- b)Statement 2 alone is sufficient, but Statement 1 alone is not.
- c)Both statements together are sufficient, but neither alone is sufficient.
- d)Each statement alone is sufficient.
- e)Neither statement is sufficient.
Correct answer is option 'C'. Can you explain this answer?
Each type A machine fills 400 cans per minute,each Type B machine fills 600 cans per minute,and each Type C machine installs 2,400 lids per minute.A lid is installed on each can that is filled and on no can that is not filled.For a particular minute,what is the total number of machines working?
(1) A total of 4,800 cans are filled that minute
(2) For that minute,there are 2 Type B machines working for every Type C machine working
(2) For that minute,there are 2 Type B machines working for every Type C machine working
a)
Statement 1 alone is sufficient, but Statement 2 alone is not.
b)
Statement 2 alone is sufficient, but Statement 1 alone is not.
c)
Both statements together are sufficient, but neither alone is sufficient.
d)
Each statement alone is sufficient.
e)
Neither statement is sufficient.
|
|
EduRev GMAT answered |
We are given that each Type A machine fills 400 cans per minute, each Type B machine fills 600 cans per minute, and each Type C machine installs 2,400 lids per minute.
We need to determine the total number of machines working for a particular minute. If we let a = the number of Type A machines needed, b = the number of Type B machines needed, and c = the number of Type C machines needed, we need to determine the value of a + b + c.
Statement One Alone:
A total of 4,800 cans are filled that minute.
Since a Type C machine installs 2,400 lids per minute, we know that we need 2 Type C machines (i.e., c = 2) to install 4,800 lids after the 4,800 cans are filled in that minute.
Since each Type A machine fills 400 cans per minute and each Type B machine fills 600 cans per minute, we have:
400a + 600b = 4,800
4a + 6b = 48
2a + 3b = 24
However, since we only have one equation but we have two variables, the values of a and b are not unique. For example, a = 12 and b = 0 OR a = 0 and b = 8.
Statement one alone is not sufficient to answer the question.
Statement Two Alone:
For that minute, there are 2 Type B machines working for every Type C machine working.\
Thus, b/c = 2/1, i.e., b = 2c; however we still cannot determine a + b + c. Statement two alone is not sufficient.
Statements One and Two Together:
From statement one, we know that c = 2 and 2a + 3b = 24, and from statement two, we know that b = 2c. Since c = 2 and b = 2c, we see that b = 4.
Next we can substitute 4 for b in the equation 2a + 3b = 24:
2a + 3(4) = 24
2a + 12 = 24
2a = 12
a = 6
Thus a + b + c = 6 + 4 + 2 = 12. We need 12 machines for that particular minute.
2a + 3(4) = 24
2a + 12 = 24
2a = 12
a = 6
Thus a + b + c = 6 + 4 + 2 = 12. We need 12 machines for that particular minute.
On Christmas Eve, Santa and 5 of his elves need to deliver 210 presents to 7 towns, with each one requiring exactly 30 presents. Each trip to a town and back takes 1 hour, several trips can be made simultaneously, and each one requires at least Santa or two elves. Santa can deliver at most 15 presents per trip, and each elf can deliver at most 10 presents per trip.
Based on the information above, select for T1 the number of minimum hours it will take to deliver all 210 presents with Santa and T2 the number of minimum hours it will take to deliver all 210 presents without Santa.
- a)T1 = 2
T2 = 3 - b)T1 = 3
T2 = 4 - c)T1 = 6
T2 = 7 - d)T1 = 7
T2 = 6 - e)T1 = 4
T2 = 5
Correct answer is option 'E'. Can you explain this answer?
On Christmas Eve, Santa and 5 of his elves need to deliver 210 presents to 7 towns, with each one requiring exactly 30 presents. Each trip to a town and back takes 1 hour, several trips can be made simultaneously, and each one requires at least Santa or two elves. Santa can deliver at most 15 presents per trip, and each elf can deliver at most 10 presents per trip.
Based on the information above, select for T1 the number of minimum hours it will take to deliver all 210 presents with Santa and T2 the number of minimum hours it will take to deliver all 210 presents without Santa.
Based on the information above, select for T1 the number of minimum hours it will take to deliver all 210 presents with Santa and T2 the number of minimum hours it will take to deliver all 210 presents without Santa.
a)
T1 = 2
T2 = 3
T2 = 3
b)
T1 = 3
T2 = 4
T2 = 4
c)
T1 = 6
T2 = 7
T2 = 7
d)
T1 = 7
T2 = 6
T2 = 6
e)
T1 = 4
T2 = 5
T2 = 5
|
|
EduRev GMAT answered |
The graph shows the number of shipments handled by each of 6 delivery companies over the past 5 years.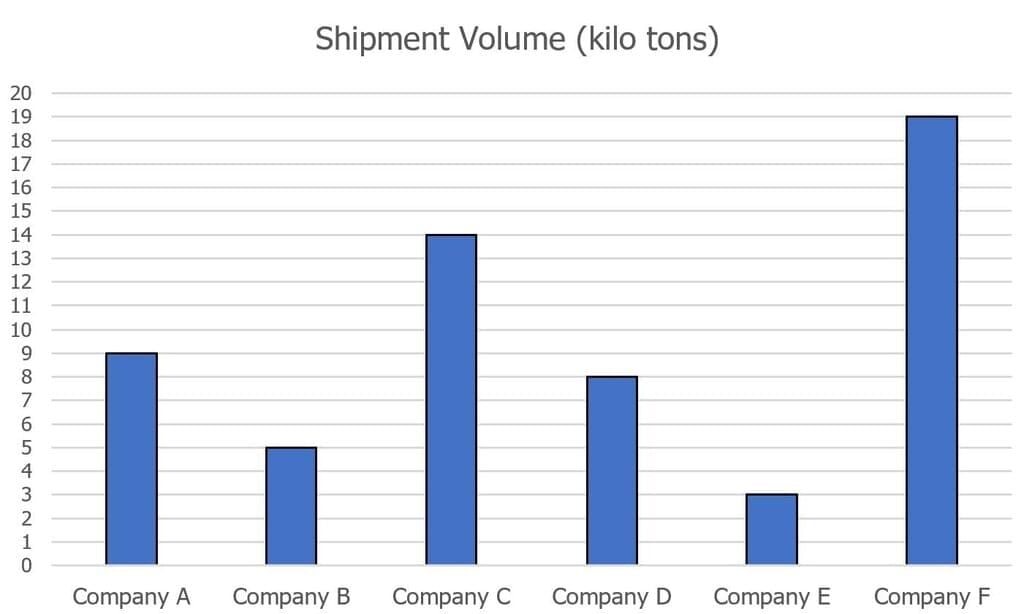
Select from each drop-down menu the option that creates the most accurate statement based on the information provided.
Over the past 5 years, the Delivery Company (i)_______ handled exactly 60% more shipments than Delivery Company (ii)________.- a)(i) Company C, (ii) Company B
- b)(i) Company E, (ii) Company A
- c)(i) Company D, (ii) Company B
- d)(i) Company E, (ii) Company C,
- e)(i) Company B, (ii) Company A
Correct answer is option 'C'. Can you explain this answer?
The graph shows the number of shipments handled by each of 6 delivery companies over the past 5 years.
Select from each drop-down menu the option that creates the most accurate statement based on the information provided.
Over the past 5 years, the Delivery Company (i)_______ handled exactly 60% more shipments than Delivery Company (ii)________.
a)
(i) Company C, (ii) Company B
b)
(i) Company E, (ii) Company A
c)
(i) Company D, (ii) Company B
d)
(i) Company E, (ii) Company C,
e)
(i) Company B, (ii) Company A
|
|
EduRev GMAT answered |
The correct answer is Company D handled exactly 60% more shipments than Delivery Company B.
To solve this question, we need to find 2 numbers such that 1.6 * x = y, where x and y are both whole numbers.
When multiplied by 1.6, only muliples of 5 (e.g. 5,10,15, etc.) result in a while number.
Only Company B satisfies this criteria with x =5.
Therefore, y must be 1.6 * 5 = 8.
To solve this question, we need to find 2 numbers such that 1.6 * x = y, where x and y are both whole numbers.
When multiplied by 1.6, only muliples of 5 (e.g. 5,10,15, etc.) result in a while number.
Only Company B satisfies this criteria with x =5.
Therefore, y must be 1.6 * 5 = 8.
The designers of a video game hired 100 game testers to play the game to determine whether the level of difficulty was appropriate. Each of the 100 testers made at most 25 attempts to complete each of the game's 15 levels (Levels 1–15). When a tester completed a level, he or she then made no further attempts at that level. For each of the levels, the table shows, among the testers who completed the level, the total number of testers whose number of attempts to complete that level fell in various ranges.
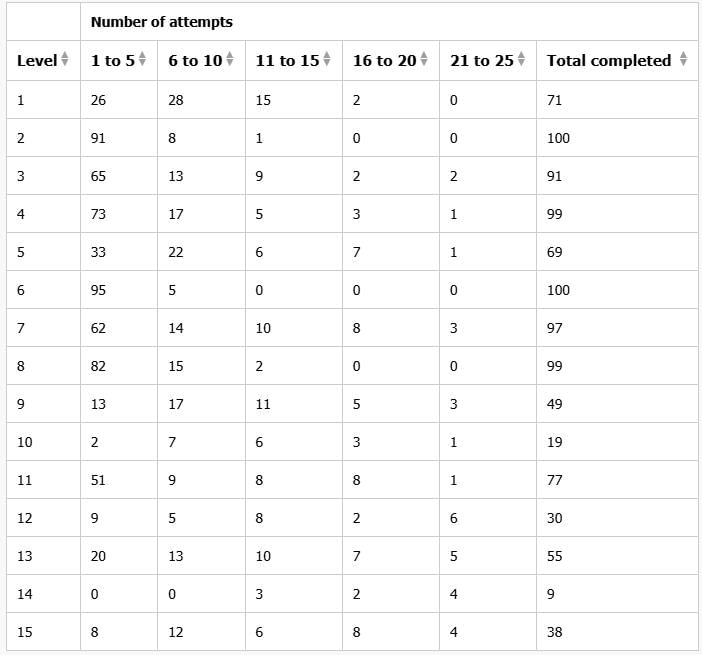For each of the following statistical measures, select Must be 20 or less for every level if, based on the information provided, the measure must be at most 20 for each of the 15 levels. Otherwise, select Could be greater than 20 for one or more.
- a)1. Could be greater than: Mean of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Median of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Range of the total number of attempts to complete for all testers who completed the level - b)1. Could be greater than: Mean of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Range of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Median of the total number of attempts to complete for all testers who completed the level - c)1. Could be greater than: Median of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Range of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Mean of the total number of attempts to complete for all testers who completed the level - d)1. Could be greater than: Mean of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Median of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Range of the total number of attempts to complete for all testers who completed the level
Correct answer is option 'A'. Can you explain this answer?
The designers of a video game hired 100 game testers to play the game to determine whether the level of difficulty was appropriate. Each of the 100 testers made at most 25 attempts to complete each of the game's 15 levels (Levels 1–15). When a tester completed a level, he or she then made no further attempts at that level. For each of the levels, the table shows, among the testers who completed the level, the total number of testers whose number of attempts to complete that level fell in various ranges.
For each of the following statistical measures, select Must be 20 or less for every level if, based on the information provided, the measure must be at most 20 for each of the 15 levels. Otherwise, select Could be greater than 20 for one or more.
a)
1. Could be greater than: Mean of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Median of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Range of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Median of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Range of the total number of attempts to complete for all testers who completed the level
b)
1. Could be greater than: Mean of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Range of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Median of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Range of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Median of the total number of attempts to complete for all testers who completed the level
c)
1. Could be greater than: Median of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Range of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Mean of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Range of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Mean of the total number of attempts to complete for all testers who completed the level
d)
1. Could be greater than: Mean of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Median of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Range of the total number of attempts to complete for all testers who completed the level
2. Must be 20 or less: Median of the total number of attempts to complete for all testers who completed the level
3. Could be greater than: Range of the total number of attempts to complete for all testers who completed the level
|
|
EduRev GMAT answered |
1. Mean of the total number of attempts to complete for all testers who completed the level.
- Check if any of the levels has more number of attempts in 15-20 and 20-25 attempts than the sum of all other columns.
- When you scan the table, the level 14 stands out as there are 3 in 11-15 attempts , 2 in 16-20 attempts and 4 in 21-25 attempts.
- So, the max mean would be when all the testers took the maximum attempt in each case, so 3 took 15 attempts, 2 took 20 attempts and 4 took 25 attempts.
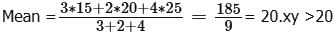
Could be greater than 20.
2. Median of the total number of attempts to complete for all testers who completed the level
- Check if any of the levels has more number of attempts in 20-25 attempts than the sum of all other columns.
- When you scan the table, no level has sum of numbers under 1-5, 6-10, 11-15 and 16-20 attempts less than that under 21-25.
- Thus median will always be 20 or less......Equal to or less than 20
3. Range of the total number of attempts to complete for all testers who completed the level
- If any level has been finished be some tester in 1-5 attempts while there are some more who have finished it in 20-25 attempts, the maximum range could be 25-1 = 24.
- There are many under this case: Level 3, 4, 5, 7, 9-15
Could be greater than 20
Alejandra is designing a game of chance. For one part of the game, a player is to randomly choose 3 marbles, without replacement, from a box containing B blue marbles, R red marbles, and no other marbles. Alejandra correctly determined the positive integers B and R so that the number of possible selections in which 1 blue marble and 2 red marbles are chosen is twice the number of possible selections in which 2 blue marbles and 1 red marble are chosen.
The positive integers B and R that Alejandra determined must be such that B is the number that is __ 1 __ and R is the number that is __ 2 __.
Based on the information provided, select for 1 and for 2 the options that create the most accurate statement. Make only two selections, one in each column.
- a)1:
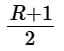
2: 2B-1 - b)1:
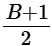
2: B-2 - c)1:
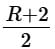
2: R+2 - d)1: 2B-1
2: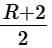 
Correct answer is option 'A'. Can you explain this answer?
Alejandra is designing a game of chance. For one part of the game, a player is to randomly choose 3 marbles, without replacement, from a box containing B blue marbles, R red marbles, and no other marbles. Alejandra correctly determined the positive integers B and R so that the number of possible selections in which 1 blue marble and 2 red marbles are chosen is twice the number of possible selections in which 2 blue marbles and 1 red marble are chosen.
The positive integers B and R that Alejandra determined must be such that B is the number that is __ 1 __ and R is the number that is __ 2 __.
Based on the information provided, select for 1 and for 2 the options that create the most accurate statement. Make only two selections, one in each column.
The positive integers B and R that Alejandra determined must be such that B is the number that is __ 1 __ and R is the number that is __ 2 __.
Based on the information provided, select for 1 and for 2 the options that create the most accurate statement. Make only two selections, one in each column.
a)
1: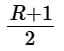
2: 2B-1
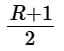
2: 2B-1
b)
1: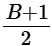
2: B-2
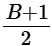
2: B-2
c)
1: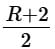
2: R+2
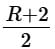
2: R+2
d)
1: 2B-1
2: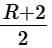
2:
|
|
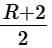
EduRev GMAT answered |
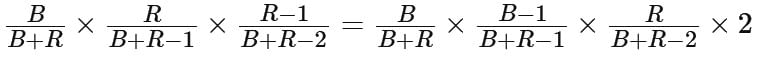
R−1 = 2B − 2
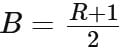
R = 2B − 1
If machine X ran continuously at a uniform rate to fill a production order, at what time did the machine finish filling the order?(1) Machine X had filled 2/3 of the order by 10:00 a.m. and 5/6 of the order by 10:30 a.m.(2) Machine X had filled 1/6 of the order by 8:30 a.m. and 1/3 of the order by 9:00 a.m.
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
If machine X ran continuously at a uniform rate to fill a production order, at what time did the machine finish filling the order?
(1) Machine X had filled 2/3 of the order by 10:00 a.m. and 5/6 of the order by 10:30 a.m.
(2) Machine X had filled 1/6 of the order by 8:30 a.m. and 1/3 of the order by 9:00 a.m.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question ask
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
EduRev GMAT answered |
Statement (1)
- At 10:00 a.m., machine X had completed 2/3 of the order.
- At 10:30 a.m., machine X had completed 5/6 of the order.
From this, we can determine the rate of the machine:
- In 30 minutes, it completed (5/6 - 2/3) = (10/12 - 8/12) = 2/12 = 1/6 of the order.
- This means the machine fills 1/6 of the order every 30 minutes.
- Since 5/6 of the order was completed by 10:30 a.m., the remaining 1/6 will take another 30 minutes, so the order is completed at 11:00 a.m
Sufficient.
Statement (2)
- At 8:30 a.m., machine X had completed 1/6 of the order.
- At 9:00 a.m., machine X had completed 1/3 of the order.
From this, we can determine the rate:
- In 30 minutes, it completed (1/3 - 1/6) = (2/6 - 1/6) = 1/6 of the order.
- Since the machine fills 1/6 of the order every 30 minutes, we can compute the completion time.
Sufficient.
Option D
- At 10:00 a.m., machine X had completed 2/3 of the order.
- At 10:30 a.m., machine X had completed 5/6 of the order.
From this, we can determine the rate of the machine:
- In 30 minutes, it completed (5/6 - 2/3) = (10/12 - 8/12) = 2/12 = 1/6 of the order.
- This means the machine fills 1/6 of the order every 30 minutes.
- Since 5/6 of the order was completed by 10:30 a.m., the remaining 1/6 will take another 30 minutes, so the order is completed at 11:00 a.m
Sufficient.
Statement (2)
- At 8:30 a.m., machine X had completed 1/6 of the order.
- At 9:00 a.m., machine X had completed 1/3 of the order.
From this, we can determine the rate:
- In 30 minutes, it completed (1/3 - 1/6) = (2/6 - 1/6) = 1/6 of the order.
- Since the machine fills 1/6 of the order every 30 minutes, we can compute the completion time.
Sufficient.
Option D
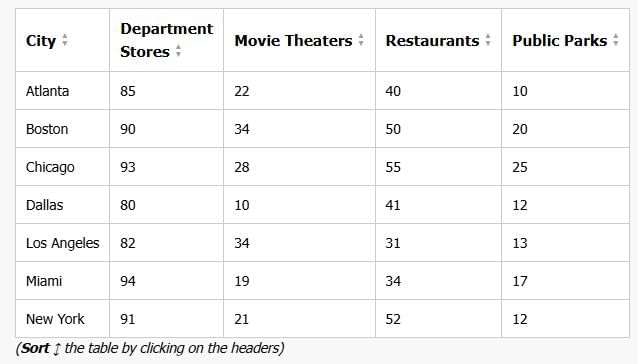
The above table shows, for different cities, the percentage of population of a city which is a regular visitor to different locations in the city. For example: 85% of the people in Atlanta are regular visitors to department stores, and 12% of the people in New York are regular visitors to public parks.
Select Would Explain if the statement explains some of the information in the table. Otherwise, select Would not Explain.
- a)Part 1: Would Not Explain
Part 2: Would Not Explain
Part 3: Would Not Explain - b)Part 1: Would Not Explain
Part 2: Would Explain
Part 3: Would Not Explain - c)Part 1: Would Not Explain
Part 2: Would Explain
Part 3: Would Explain - d)Part 1: Would Explain
Part 2: Would Explain
Part 3: Would Explain - e)Part 1: Would Explain
Part 2: Would Not Explain
Part 3: Would Not Explain
Correct answer is option 'A'. Can you explain this answer?
The above table shows, for different cities, the percentage of population of a city which is a regular visitor to different locations in the city. For example: 85% of the people in Atlanta are regular visitors to department stores, and 12% of the people in New York are regular visitors to public parks.
Select Would Explain if the statement explains some of the information in the table. Otherwise, select Would not Explain.
a)
Part 1: Would Not Explain
Part 2: Would Not Explain
Part 3: Would Not Explain
Part 2: Would Not Explain
Part 3: Would Not Explain
b)
Part 1: Would Not Explain
Part 2: Would Explain
Part 3: Would Not Explain
Part 2: Would Explain
Part 3: Would Not Explain
c)
Part 1: Would Not Explain
Part 2: Would Explain
Part 3: Would Explain
Part 2: Would Explain
Part 3: Would Explain
d)
Part 1: Would Explain
Part 2: Would Explain
Part 3: Would Explain
Part 2: Would Explain
Part 3: Would Explain
e)
Part 1: Would Explain
Part 2: Would Not Explain
Part 3: Would Not Explain
Part 2: Would Not Explain
Part 3: Would Not Explain
|
|
EduRev GMAT answered |
A. A majority of people living in these cities do not have easy access to a public park.
>>ACCESS – cant not be commented ; maybe these visitors are not interested to go even after having access
WOULD NOT EXPLAIN
B. The proportion of residents that live in the proximity of a movie theater is lower in Dallas than that in Boston and Los Angeles.
>>Dallas= 41% ; boston = 50% and LA= 31%
But it is hard to mention the number of residents in total
WOULD NOT EXPLAIN
C. The proportion if people who prefer to spend time indoors is greater in Dallas than in Chicago.
>>Dallas indoors= it is not right to explain that 82% in departmental stores are same people or different people moving to theatres, restaurants or public parks
Similarly for Chicago ; no detail infromtion is given
WOULD NOT EXPLAIN
>>ACCESS – cant not be commented ; maybe these visitors are not interested to go even after having access
WOULD NOT EXPLAIN
B. The proportion of residents that live in the proximity of a movie theater is lower in Dallas than that in Boston and Los Angeles.
>>Dallas= 41% ; boston = 50% and LA= 31%
But it is hard to mention the number of residents in total
WOULD NOT EXPLAIN
C. The proportion if people who prefer to spend time indoors is greater in Dallas than in Chicago.
>>Dallas indoors= it is not right to explain that 82% in departmental stores are same people or different people moving to theatres, restaurants or public parks
Similarly for Chicago ; no detail infromtion is given
WOULD NOT EXPLAIN
Which of the following fractions is the largest?- a)2/7
- b)2/3
- c)7/9
- d)7/12
- e)3/5
Correct answer is option 'C'. Can you explain this answer?
Which of the following fractions is the largest?
a)
2/7
b)
2/3
c)
7/9
d)
7/12
e)
3/5
|
|
Akshay Khanna answered |
The best answer is C.
Lets compare all the answers to 2/7, unless we find a larger fraction.
(b) 2/3 is larger than 2/7. For now, this is the right answer.
(c) 2/3 is also 6/9 and that is smaller than 7/9. For now this is the right answer.
(d) 7/9 is bigger than 7/12
(e) Bring this answer and (c) to a common denominator.7/9 = 35/45 and 3/5 = 27/45.
7/9 is the largest fraction.
Lets compare all the answers to 2/7, unless we find a larger fraction.
(b) 2/3 is larger than 2/7. For now, this is the right answer.
(c) 2/3 is also 6/9 and that is smaller than 7/9. For now this is the right answer.
(d) 7/9 is bigger than 7/12
(e) Bring this answer and (c) to a common denominator.7/9 = 35/45 and 3/5 = 27/45.
7/9 is the largest fraction.
a, b, k, s are different non-zero integers, 2/a + 4/b = k/s and k/s is maximally reduced. Does s = ab?1. a and b are primes
2. a and b have gcd = 1- a)Statement 1 alone is sufficient, but Statement 2 alone is not.
- b)Statement 2 alone is sufficient, but Statement 1 alone is not.
- c)Both statements together are sufficient, but neither alone is sufficient.
- d)Each statement alone is sufficient.
- e)Neither statement is sufficient.
Correct answer is option 'D'. Can you explain this answer?
a, b, k, s are different non-zero integers, 2/a + 4/b = k/s and k/s is maximally reduced. Does s = ab?
1. a and b are primes
2. a and b have gcd = 1
2. a and b have gcd = 1
a)
Statement 1 alone is sufficient, but Statement 2 alone is not.
b)
Statement 2 alone is sufficient, but Statement 1 alone is not.
c)
Both statements together are sufficient, but neither alone is sufficient.
d)
Each statement alone is sufficient.
e)
Neither statement is sufficient.
|
|
EduRev GMAT answered |
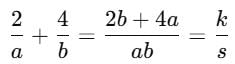
Since k/s in its simplest form, s must be the denominator in its irreducible form, which is ab/gcd(2b + 4a,ab).
Statement 1: If a and b are primes, their product ab has no common factors with 2a + 4b (except possibly 2, but that won't affect the full fraction’s reducibility). Hence, s = ab.
Statement 2: If gcd (a, b) = 1, the same reasoning applies, as gcd(2b + 4a, ab) will still be 1. Thus, s = ab.
Since each statement alone guarantees the answer, the correct choice is D.
Since each statement alone guarantees the answer, the correct choice is D.
Consider each of the following statements. Does the information in the three sources support the inference as stated?
- a)Part 1: No
Part 2: No
Part 3: No - b)Part 1: Yes
Part 2: No
Part 3:Yes - c)Part 1: No
Part 2: Yes
Part 3:No - d)Part 1: Yes
Part 2: Yes
Part 3: Yes - e)Part 1: NO
Part 2: NO
Part 3: Yes
Correct answer is option 'A'. Can you explain this answer?
Consider each of the following statements. Does the information in the three sources support the inference as stated?
a)
Part 1: No
Part 2: No
Part 3: No
Part 2: No
Part 3: No
b)
Part 1: Yes
Part 2: No
Part 3:Yes
Part 2: No
Part 3:Yes
c)
Part 1: No
Part 2: Yes
Part 3:No
Part 2: Yes
Part 3:No
d)
Part 1: Yes
Part 2: Yes
Part 3: Yes
Part 2: Yes
Part 3: Yes
e)
Part 1: NO
Part 2: NO
Part 3: Yes
Part 2: NO
Part 3: Yes
|
|
EduRev GMAT answered |
Part 1: The median retail cost of the product line is $20.40.
The median retail cost of product is $34.
Hence, the answer is No.
Part 2: Loyal members who purchase online save more than 50% off the cost of their total purchases and shipping compared to nonmembers.
Let x be the shipping cost.
Let's consider a member and a non member purchase 1 unit of Renew Soap.
Cost for member = 27
Cost for non member = 45 + x
Savings of a member compared to a non member = 18 + x
Translating the question statement: Is (18 + x) more than 50% of (45 + x)
Is (18 + x) > (45 + x)/2
Is (18+x)/(45+x) > 1/2
We can clearly see that the answer is No.
Hence, the final answer is No.
Part 3: The minimum purchase amount within the 6-month introductory period is less than the $50.00 charge issued to accounts that are canceled early.
The minimum amount within the 6 month introductory period = Price of Detox Tea * 6 = 10.2 *6 = $61.2
Hence, the answer is No.
The median retail cost of product is $34.
Hence, the answer is No.
Part 2: Loyal members who purchase online save more than 50% off the cost of their total purchases and shipping compared to nonmembers.
Let x be the shipping cost.
Let's consider a member and a non member purchase 1 unit of Renew Soap.
Cost for member = 27
Cost for non member = 45 + x
Savings of a member compared to a non member = 18 + x
Translating the question statement: Is (18 + x) more than 50% of (45 + x)
Is (18 + x) > (45 + x)/2
Is (18+x)/(45+x) > 1/2
We can clearly see that the answer is No.
Hence, the final answer is No.
Part 3: The minimum purchase amount within the 6-month introductory period is less than the $50.00 charge issued to accounts that are canceled early.
The minimum amount within the 6 month introductory period = Price of Detox Tea * 6 = 10.2 *6 = $61.2
Hence, the answer is No.
Multiple Sleep Latency TestThe multiple sleep latency test (MSLT) is the most widely used objective assessment procedure for excessive daytime sleepiness. It consists of a series of five nap opportunities given every two hours in a sleep laboratory. The patient lies in a darkened, sound-attenuated room for up to 20 minutes and is instructed to fall asleep. The average latency to sleep onset over all nap opportunities provides an index of sleep propensity.
As a general guideline, only mean sleep latencies shorter than 8 minutes on an MSLT are considered abnormal, and latencies shorter than 5 minutes are taken to indicate severe excessive daytime sleepiness. A patient with a mean sleep latency of 2 minutes or less on an MSLT is unlikely to be exaggerating a complaint of excessive daytime sleepiness, to suffer from fatigue rather than sleepiness, or to be free of any sleep disorder.Patient Data - Ramesh is a 34-year-old man with no major health problems who takes no prescription medicines.
- Sara is a 23-year-old woman with asthma who takes a prescription stimulant daily for treatment.
- Angel is a 72-year-old woman with major depressive disorder who takes a prescription anti-depressant daily.
- John is an 11-year-old child who has been diagnosed with ADD, but does not take any prescription medications.
- Steve is a 54-year-old man with mild heart disease who takes several over-the-counter supplements.
MSLT Results
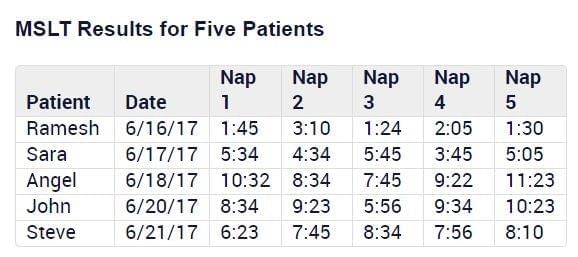
NOTE: Data given is time until sleep in minutes and seconds. Results may be misleading if they are affected by patient age (different criteria apply for children under 16), noise in the sleep center, patient anxiety during the test, or atypical sleep on the previous night. Use of prescription medications such as stimulants or antidepressants can also lead to misleading results.Based on the information presented, some of the patients have MSLT data that could be misleading and others do not. For the following statements, select Yes if the scenario provided would change that status for any of the five patients. Otherwise select No.
- a)Part 1: Yes
Part 2: No
Part 3: Yes - b)Part 1: No
Part 2: No
Part 3: Yes - c)Part 1: Yes
Part 2: Yes
Part 3: Yes - d)Part 1: No
Part 2: No
Part 3: Yes
Correct answer is option 'B'. Can you explain this answer?
Multiple Sleep Latency Test
The multiple sleep latency test (MSLT) is the most widely used objective assessment procedure for excessive daytime sleepiness. It consists of a series of five nap opportunities given every two hours in a sleep laboratory. The patient lies in a darkened, sound-attenuated room for up to 20 minutes and is instructed to fall asleep. The average latency to sleep onset over all nap opportunities provides an index of sleep propensity.
As a general guideline, only mean sleep latencies shorter than 8 minutes on an MSLT are considered abnormal, and latencies shorter than 5 minutes are taken to indicate severe excessive daytime sleepiness. A patient with a mean sleep latency of 2 minutes or less on an MSLT is unlikely to be exaggerating a complaint of excessive daytime sleepiness, to suffer from fatigue rather than sleepiness, or to be free of any sleep disorder.
As a general guideline, only mean sleep latencies shorter than 8 minutes on an MSLT are considered abnormal, and latencies shorter than 5 minutes are taken to indicate severe excessive daytime sleepiness. A patient with a mean sleep latency of 2 minutes or less on an MSLT is unlikely to be exaggerating a complaint of excessive daytime sleepiness, to suffer from fatigue rather than sleepiness, or to be free of any sleep disorder.
Patient Data
- Ramesh is a 34-year-old man with no major health problems who takes no prescription medicines.
- Sara is a 23-year-old woman with asthma who takes a prescription stimulant daily for treatment.
- Angel is a 72-year-old woman with major depressive disorder who takes a prescription anti-depressant daily.
- John is an 11-year-old child who has been diagnosed with ADD, but does not take any prescription medications.
- Steve is a 54-year-old man with mild heart disease who takes several over-the-counter supplements.
MSLT Results
NOTE: Data given is time until sleep in minutes and seconds. Results may be misleading if they are affected by patient age (different criteria apply for children under 16), noise in the sleep center, patient anxiety during the test, or atypical sleep on the previous night. Use of prescription medications such as stimulants or antidepressants can also lead to misleading results.
Based on the information presented, some of the patients have MSLT data that could be misleading and others do not. For the following statements, select Yes if the scenario provided would change that status for any of the five patients. Otherwise select No.
a)
Part 1: Yes
Part 2: No
Part 3: Yes
Part 2: No
Part 3: Yes
b)
Part 1: No
Part 2: No
Part 3: Yes
Part 2: No
Part 3: Yes
c)
Part 1: Yes
Part 2: Yes
Part 3: Yes
Part 2: Yes
Part 3: Yes
d)
Part 1: No
Part 2: No
Part 3: Yes
Part 2: No
Part 3: Yes
|
|
EduRev GMAT answered |
1. [no] There was a major noise disturbance in the sleep center on 6/17/17.
- Sara was tested on that date and she already had misleading data. So, her status of whether she has misleading data does not change (she had misleading data before, and now after the noise she still has misleading data, even if the actual data changes further)
2. [no] None of the patients who had a sleep test after 6/17 suffered from anxiety during the test.
- Steve anyway does not suffer from anxiety. For Angel and John, data was not reliable before either due to other reasons. So, status does not change.
3. [yes] All of the patients less than 50 years of age had atypical sleep the night before the test.
- This will change Ramesh and Steve's data from "not misleading" to "misleading".
- Sara was tested on that date and she already had misleading data. So, her status of whether she has misleading data does not change (she had misleading data before, and now after the noise she still has misleading data, even if the actual data changes further)
2. [no] None of the patients who had a sleep test after 6/17 suffered from anxiety during the test.
- Steve anyway does not suffer from anxiety. For Angel and John, data was not reliable before either due to other reasons. So, status does not change.
3. [yes] All of the patients less than 50 years of age had atypical sleep the night before the test.
- This will change Ramesh and Steve's data from "not misleading" to "misleading".
If the information contained in all three sources is correct, the member price of
an item that retails for $65.00 will be closest to:- a)$26.00
- b)$28.70
- c)$32.40
- d)$39.00
Correct answer is option 'D'. Can you explain this answer?
If the information contained in all three sources is correct, the member price of
an item that retails for $65.00 will be closest to:
a)
$26.00
b)
$28.70
c)
$32.40
d)
$39.00
|
|
EduRev GMAT answered |
Member Price = 60% of 65 = $39
Hence, the answer is $39.
Hence, the answer is $39.
According to a survey, at least 70% of students in a college study Hindi, at least 75% of students study French, and at least 80% of students study German. If x is the minimum percentage of students who study all three languages and y is the maximum percentage of students who study all three languages, then choose the appropriate values for x and y from the table given below:
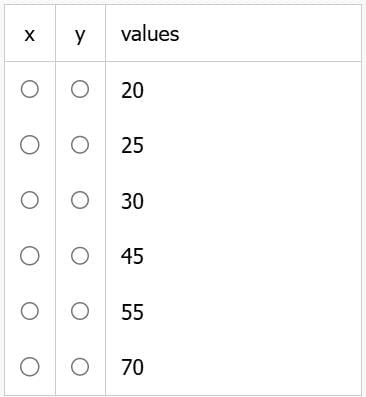
- a)x=25, y=70
- b)x=20, y=30
- c)x=45, y=55
- d)x=55, y=70
Correct answer is option 'A'. Can you explain this answer?
According to a survey, at least 70% of students in a college study Hindi, at least 75% of students study French, and at least 80% of students study German. If x is the minimum percentage of students who study all three languages and y is the maximum percentage of students who study all three languages, then choose the appropriate values for x and y from the table given below:
a)
x=25, y=70
b)
x=20, y=30
c)
x=45, y=55
d)
x=55, y=70
|
|
EduRev GMAT answered |
For y i.e. maximum, we have at least 70, 75 and 80. Here, the minimum of subsets is 70 so y=70%.
For x, we can get minimum if we assume students studying both subjects as the maximum.
Let, total students=100a. H=70a, F=75a, G=80a.
100a=70a+75a+80a - 100a (assuming maximum) - x
200a-225a=-x or, x=25a i.e. 25%.
x=25, y=70.
For x, we can get minimum if we assume students studying both subjects as the maximum.
Let, total students=100a. H=70a, F=75a, G=80a.
100a=70a+75a+80a - 100a (assuming maximum) - x
200a-225a=-x or, x=25a i.e. 25%.
x=25, y=70.
Jaspher invested in two ventures A and B, with rates of interest at 5k% and 3k%, respectively. What was the initial investment Jaspher made in venture B?(1) The amount Jaspher invested in venture B was five times the amount he invested in venture A.(2) The interest from venture B was $150 while the interest from venture A was $50.- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'E'. Can you explain this answer?
Jaspher invested in two ventures A and B, with rates of interest at 5k% and 3k%, respectively. What was the initial investment Jaspher made in venture B?
(1) The amount Jaspher invested in venture B was five times the amount he invested in venture A.
(2) The interest from venture B was $150 while the interest from venture A was $50.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
EduRev GMAT answered |
Answer:(E)
Let the initial investment in venture A be denoted as 'a', and the initial investment in venture B be 'b'.
The question is asking for the value of 'b'.
Statement (1):
This statement tells you that the initial investment in venture B is five times the initial investment in venture A.
In mathematical terms, this gives you b = 5a.
However, without knowing the value of 'a', you cannot determine the value of 'b'. Thus, statement (1) alone is not sufficient.
Statement (2):
This statement tells you that 'a' dollars earning interest at a rate of 5k% equals $50, and 'b' dollars earning interest at a rate of 3k% equals $150.
This gives you two equations: 5k/100 * a = $50 and
3k/100 * b = $150.
Manipulating these equations, we get:
a = $50 / (5k/100) and
b = $150 / (3k/100)
Dividing, these we get,
a/b = 1/5
However, we can't figure out the individual values of 'a' and 'b' as the value of 'k' is not given. So, statement (2) alone is also not sufficient.
Taking BOTH statements TOGETHER, we still can't determine the value of 'b' because we do not know the value of 'k'. Both statements together simply confirm that b = 5a, but without the value of 'k', we cannot determine the individual values of 'a' and 'b'. Therefore, BOTH statements TOGETHER are NOT sufficient.
The correct answer is (E).
Archeologists excavating at a certain site have found the following five artifacts: a bowl, a cup, a jug, a statue, and an urn. At this site, the greater the depth at which an artifact was found, the older that artifact is. The bowl was determined to be x years old and was found at a depth of d meters. Both the cup and the jug were found at a depth of less than d meters. The statue was determined to be 1.5x years old, and the urn was found at a greater depth than the statue was.Each of the following statements pertains to the five artifacts found at the site. Assuming that the information provided is correct, select for Must be true the statement that must be true and select for Must be false the statement that must be false. Make only two selections, one in each column.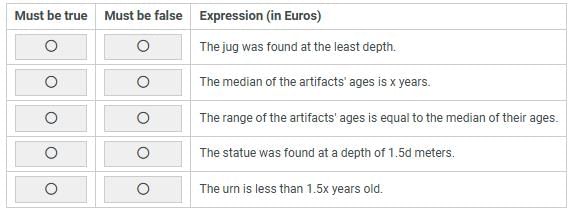
- a)Must be True: The jug was found at the least depth.
Must be False: The range of the artifacts' ages is equal to the median of their ages. - b)Must be False: The median of the artifacts' ages is x years
Must be False: The urn is less than 1.5x years old- must be false. - c)Must be true: The median of the artifacts' ages is x years
Must be false: The urn is less than 1.5x years old- must be false. - d)Must be True: The jug was found at the least depth.
Must be True: The range of the artifacts' ages is equal to the median of their ages. - e)Must be False: The median of the artifacts' ages is x years
Must be True: The urn is less than 1.5x years old- must be false.
Correct answer is option 'C'. Can you explain this answer?
Archeologists excavating at a certain site have found the following five artifacts: a bowl, a cup, a jug, a statue, and an urn. At this site, the greater the depth at which an artifact was found, the older that artifact is. The bowl was determined to be x years old and was found at a depth of d meters. Both the cup and the jug were found at a depth of less than d meters. The statue was determined to be 1.5x years old, and the urn was found at a greater depth than the statue was.
Each of the following statements pertains to the five artifacts found at the site. Assuming that the information provided is correct, select for Must be true the statement that must be true and select for Must be false the statement that must be false. Make only two selections, one in each column.
a)
Must be True: The jug was found at the least depth.
Must be False: The range of the artifacts' ages is equal to the median of their ages.
Must be False: The range of the artifacts' ages is equal to the median of their ages.
b)
Must be False: The median of the artifacts' ages is x years
Must be False: The urn is less than 1.5x years old- must be false.
Must be False: The urn is less than 1.5x years old- must be false.
c)
Must be true: The median of the artifacts' ages is x years
Must be false: The urn is less than 1.5x years old- must be false.
Must be false: The urn is less than 1.5x years old- must be false.
d)
Must be True: The jug was found at the least depth.
Must be True: The range of the artifacts' ages is equal to the median of their ages.
Must be True: The range of the artifacts' ages is equal to the median of their ages.
e)
Must be False: The median of the artifacts' ages is x years
Must be True: The urn is less than 1.5x years old- must be false.
Must be True: The urn is less than 1.5x years old- must be false.
|
|
EduRev GMAT answered |
- The greater the depth at which an artifact was found, the older that artifact is.
- The bowl was determined to be x years old and was found at a depth of d meters.
- Both the cup and the jug were found at a depth of less than d meters.
- The statue was determined to be 1.5x years old, and the urn was found at a greater depth than the statue was.
- The order of age from oldest to youngest is: urn, statue, bowl, {cup, jug}. The order of depth from deepest to shallowest is: urn, statue, bowl, {cup, jug}.
"Must be True" choice:
- "The median of the artifacts' ages is x years." To evaluate this statement, we need to arrange the artifacts in the order of their age. The median is the middle value when all values are sorted in ascending or descending order. Here, the bowl is the middle artifact in terms of age, and the bowl is x years old. Therefore, the median age is x years.
"Must be False" choice:
- "The urn is less than 1.5x years old." Given that the urn was found at a greater depth than the statue, and that a greater depth corresponds to an older age, we can deduce that the urn is older than the statue. We know the statue is 1.5x years old, so the urn must be older than 1.5x years. Therefore, the statement "the urn is less than 1.5x years old" must be false.
Five amateur runners are competing with one another during a series of 20 designated 10 km training runs. A prize of $50 will be awarded to the runner with the overall fastest time (the fastest among all of the times in all of the runs), and a prize of $30 to the runner with the individual time that shows the greatest improvement (decrease in time) from that runner's time for the first of the designated runs. The times are shown in the table in minutes and seconds. The times for the first run are shown in boldface.
For each of the following statements, select Yes if the statement is accurate, based on the information provided. Otherwise, select No.
- a)Yes: Runner D will be awarded the $50 prize.
No: Runner A will be awarded the $30 prize.
Yes: Both prizes will be awarded to the same Individual - b)No: Runner D will be awarded the $50 prize.
No: Runner A will be awarded the $30 prize.
Yes: Both prizes will be awarded to the same Individual - c)Yes: Runner D will be awarded the $50 prize.
No: Runner A will be awarded the $30 prize.
No: Both prizes will be awarded to the same Individual - d)No: Runner D will be awarded the $50 prize.
No: Runner A will be awarded the $30 prize.
No: Both prizes will be awarded to the same Individual
Correct answer is option 'B'. Can you explain this answer?
Five amateur runners are competing with one another during a series of 20 designated 10 km training runs. A prize of $50 will be awarded to the runner with the overall fastest time (the fastest among all of the times in all of the runs), and a prize of $30 to the runner with the individual time that shows the greatest improvement (decrease in time) from that runner's time for the first of the designated runs. The times are shown in the table in minutes and seconds. The times for the first run are shown in boldface.
For each of the following statements, select Yes if the statement is accurate, based on the information provided. Otherwise, select No.
a)
Yes: Runner D will be awarded the $50 prize.
No: Runner A will be awarded the $30 prize.
Yes: Both prizes will be awarded to the same Individual
No: Runner A will be awarded the $30 prize.
Yes: Both prizes will be awarded to the same Individual
b)
No: Runner D will be awarded the $50 prize.
No: Runner A will be awarded the $30 prize.
Yes: Both prizes will be awarded to the same Individual
No: Runner A will be awarded the $30 prize.
Yes: Both prizes will be awarded to the same Individual
c)
Yes: Runner D will be awarded the $50 prize.
No: Runner A will be awarded the $30 prize.
No: Both prizes will be awarded to the same Individual
No: Runner A will be awarded the $30 prize.
No: Both prizes will be awarded to the same Individual
d)
No: Runner D will be awarded the $50 prize.
No: Runner A will be awarded the $30 prize.
No: Both prizes will be awarded to the same Individual
No: Runner A will be awarded the $30 prize.
No: Both prizes will be awarded to the same Individual
|
|
EduRev GMAT answered |
Answering this question isn't particularly complicated. Basically, we just have to find a fastest time and find the biggest difference between the runners' first times and fastest times.
At the same time, getting this question correct can be a little tough because, when we sort the table, we can get the impression that we've found the value we need when actually we haven't.
So, one key move we need to make to get this question correct is to sort on each runner individually when we're looking for the runners' fastest times. If we fail to do that, we could get the impression that we're using a runner's fastest time when we're actually using another time.
Runner D will be awarded the $50 prize.
This statement is fairly straightforward to handle. The $50 prize will be awarded to the runner with "the overall fastest time (the fastest among all of the times in all of the runs)." So, we just have to find the single fastest time in the table and see whether that time belongs to Runner D.
To do so, we sort each runner's column individually from lowest to highest. Sorted, each column shows a runner's fastest time at the top since the lowest number is the runner's fastest time.
Here's what we find at the top of the runners' sorted columns:
At the same time, getting this question correct can be a little tough because, when we sort the table, we can get the impression that we've found the value we need when actually we haven't.
So, one key move we need to make to get this question correct is to sort on each runner individually when we're looking for the runners' fastest times. If we fail to do that, we could get the impression that we're using a runner's fastest time when we're actually using another time.
Runner D will be awarded the $50 prize.
This statement is fairly straightforward to handle. The $50 prize will be awarded to the runner with "the overall fastest time (the fastest among all of the times in all of the runs)." So, we just have to find the single fastest time in the table and see whether that time belongs to Runner D.
To do so, we sort each runner's column individually from lowest to highest. Sorted, each column shows a runner's fastest time at the top since the lowest number is the runner's fastest time.
Here's what we find at the top of the runners' sorted columns:
- Runner A: '39:01
- Runner B: ‘38:02
- Runner C: ‘37:29
- Runner D: ‘37:56
- Runner E: ‘38:11
We see that the lowest value of the five is Runner C's fastest time.
So, Runner C, rather than Runner D, will get the $50 prize.
Select No.
So, Runner C, rather than Runner D, will get the $50 prize.
Select No.
Runner A will be awarded the $30 prize.
To determine whether this statement is true, we'll compare each runner's first time with that runner's fastest time by sorting on Run # to bring up the runner's first time and then sorting on the individual runner to bring up the runner's fastest time.
Checking this statement takes a little more work, but once again, the key to getting this one right is being careful to sort the columns individually to compare each runner's first time with that runner's fastest time.
Also, we don't have to calculate exact differences between first times and fastest times. We can eliminate some runners quickly by estimating roughly and then be more exact if we have to with any that are close.
Finally, if we've read all the statements, we can see that, in checking this statement, we can also check the third statement since, to check the third statement, we have to determine which individual will get the $30 prize.
Here's what we get for the difference between the first and fastest time for each runner:
To determine whether this statement is true, we'll compare each runner's first time with that runner's fastest time by sorting on Run # to bring up the runner's first time and then sorting on the individual runner to bring up the runner's fastest time.
Checking this statement takes a little more work, but once again, the key to getting this one right is being careful to sort the columns individually to compare each runner's first time with that runner's fastest time.
Also, we don't have to calculate exact differences between first times and fastest times. We can eliminate some runners quickly by estimating roughly and then be more exact if we have to with any that are close.
Finally, if we've read all the statements, we can see that, in checking this statement, we can also check the third statement since, to check the third statement, we have to determine which individual will get the $30 prize.
Here's what we get for the difference between the first and fastest time for each runner:
- Runner A: ‘41:53 - '39:01 ≈ 42 - 39 ≈ 3
- Runner B: ‘40:18 - ‘38:02 ≈ 2.25
- Runner C: ‘41:26 - ‘37:29 ≈ 41.5 - 37.5 ≈ 4
- Runner D: ‘41:33 - ‘37:56 ≈ 41.5 - 38 ≈ 3.5
- Runner E: ‘41:25 - ‘38:11 ≈ 41.5 - 38.25 ≈ 3.25
We see the Runner C has the biggest difference, and we could have stopped checking at Runner C for this statement, but we needed to check Runner D and Runner E to check the next statement. So, if we've already read the next statement, we can get two statements done together by checking all the runners at once.
In any case, we see that Runner C rather than Runner A improved the most.
Select No.
In any case, we see that Runner C rather than Runner A improved the most.
Select No.
Both prizes will be awarded to the same individual.
In checking the above two statements, we've found that Runner C had the fastest time and improved the most.
If we hadn't calculated improvements for Runner D and Runner E when we checked the previous statement, we could have done it now to confirm that Runner C improved the most.
In any case, it's true that both prizes will be awarded to the same individual, Runner C.
Select Yes.
In checking the above two statements, we've found that Runner C had the fastest time and improved the most.
If we hadn't calculated improvements for Runner D and Runner E when we checked the previous statement, we could have done it now to confirm that Runner C improved the most.
In any case, it's true that both prizes will be awarded to the same individual, Runner C.
Select Yes.
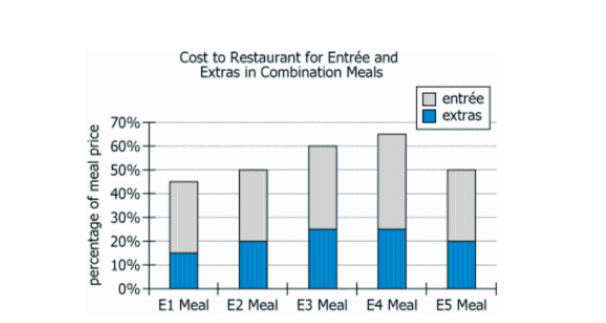
A certain restaurant serves exactly 5 entrées—E1 through E5. Customers may order an entrée alone, but most customers order an entrée as part of a combination meal, which consists of one entrée plus extras—a side dish and drink. While the entrées vary in cost to the restaurant, the extras always have the same cost to the restaurant. The graph shows the actual cost to the restaurant for the entrée and the extras as a percent of the price charged for the meal.Based on the information provided, select from each drop-down menu the option that creates the most accurate statement.
1. Of the five combination meals, the meal with entrée _____ has the highest price.
2. Of the five combination meals, the sale of a single meal with entrée ______ nets the least profit.- a)1: E2
2: E3 - b)1: E1
2: E4 - c)1: E4
2: E3 - d)1: E5
2: E3
Correct answer is option 'B'. Can you explain this answer?
A certain restaurant serves exactly 5 entrées—E1 through E5. Customers may order an entrée alone, but most customers order an entrée as part of a combination meal, which consists of one entrée plus extras—a side dish and drink. While the entrées vary in cost to the restaurant, the extras always have the same cost to the restaurant. The graph shows the actual cost to the restaurant for the entrée and the extras as a percent of the price charged for the meal.
Based on the information provided, select from each drop-down menu the option that creates the most accurate statement.
1. Of the five combination meals, the meal with entrée _____ has the highest price.
2. Of the five combination meals, the sale of a single meal with entrée ______ nets the least profit.
1. Of the five combination meals, the meal with entrée _____ has the highest price.
2. Of the five combination meals, the sale of a single meal with entrée ______ nets the least profit.
a)
1: E2
2: E3
2: E3
b)
1: E1
2: E4
2: E4
c)
1: E4
2: E3
2: E3
d)
1: E5
2: E3
2: E3
|
|
EduRev GMAT answered |
1: Since the extras always have the same cost to the restaurant, that cost must be lowest as a percentage of the highest price charged for a combination meal.
The graph shows the extras cost only about 15% of the price charged for the combination meal with entrée E1, but at least 20% of the price charged for each of the other combination meals. So, the combination meal with entrée E1 has the highest price.
The correct answer is E1.
The graph shows the extras cost only about 15% of the price charged for the combination meal with entrée E1, but at least 20% of the price charged for each of the other combination meals. So, the combination meal with entrée E1 has the highest price.
The correct answer is E1.
2. Let's assume that apart from the costs shown in the graph, any other costs to the restaurant are the same for each combination meal served.
Out of the sales price of a combination meal, the percentage profits to the restaurant are then lower for combination meals whose total percentage costs shown in the graph are higher.
The total percentage costs shown in the graph are highest for the combination meal with entrée E4, so this meal must net the least profit as a percentage of its sales price.
Next, note that the graph shows that the extras cost at least as high a percentage of this meal's sales price as of any of the other combination meals' sales prices.
That means this meal must have a sales price no higher than any of the other combination meals do.
So, because the meal with entrée E4 nets the least profit as a percentage of its sales price, and that sales price is no higher than any other combination meal's sales price, the meal with entree E4 must net the least total amount prcfit per meal served.
The correct answer is E4.
Out of the sales price of a combination meal, the percentage profits to the restaurant are then lower for combination meals whose total percentage costs shown in the graph are higher.
The total percentage costs shown in the graph are highest for the combination meal with entrée E4, so this meal must net the least profit as a percentage of its sales price.
Next, note that the graph shows that the extras cost at least as high a percentage of this meal's sales price as of any of the other combination meals' sales prices.
That means this meal must have a sales price no higher than any of the other combination meals do.
So, because the meal with entrée E4 nets the least profit as a percentage of its sales price, and that sales price is no higher than any other combination meal's sales price, the meal with entree E4 must net the least total amount prcfit per meal served.
The correct answer is E4.
Multiple Sleep Latency TestThe multiple sleep latency test (MSLT) is the most widely used objective assessment procedure for excessive daytime sleepiness. It consists of a series of five nap opportunities given every two hours in a sleep laboratory. The patient lies in a darkened, sound-attenuated room for up to 20 minutes and is instructed to fall asleep. The average latency to sleep onset over all nap opportunities provides an index of sleep propensity.
As a general guideline, only mean sleep latencies shorter than 8 minutes on an MSLT are considered abnormal, and latencies shorter than 5 minutes are taken to indicate severe excessive daytime sleepiness. A patient with a mean sleep latency of 2 minutes or less on an MSLT is unlikely to be exaggerating a complaint of excessive daytime sleepiness, to suffer from fatigue rather than sleepiness, or to be free of any sleep disorder.Patient Data - Ramesh is a 34-year-old man with no major health problems who takes no prescription medicines.
- Sara is a 23-year-old woman with asthma who takes a prescription stimulant daily for treatment.
- Angel is a 72-year-old woman with major depressive disorder who takes a prescription anti-depressant daily.
- John is an 11-year-old child who has been diagnosed with ADD, but does not take any prescription medications.
- Steve is a 54-year-old man with mild heart disease who takes several over-the-counter supplements.
MSLT Results
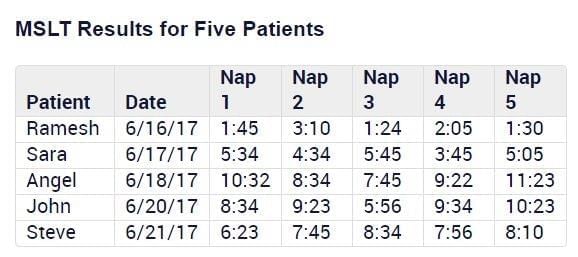
NOTE: Data given is time until sleep in minutes and seconds. Results may be misleading if they are affected by patient age (different criteria apply for children under 16), noise in the sleep center, patient anxiety during the test, or atypical sleep on the previous night. Use of prescription medications such as stimulants or antidepressants can also lead to misleading results.Which of the following can be reasonably inferred from the data provided?
- a)John’s MSLT results fall within normal guidelines.
- b)Angel has exaggerated her claim of daytime sleepiness.
- c)Ramesh may suffer from some type of sleep disorder.
- d)John does not suffer from a sleep disorder.
- e)Sara suffers from fatigue, not excessive daytime sleepiness.
Correct answer is option 'C'. Can you explain this answer?
Multiple Sleep Latency Test
The multiple sleep latency test (MSLT) is the most widely used objective assessment procedure for excessive daytime sleepiness. It consists of a series of five nap opportunities given every two hours in a sleep laboratory. The patient lies in a darkened, sound-attenuated room for up to 20 minutes and is instructed to fall asleep. The average latency to sleep onset over all nap opportunities provides an index of sleep propensity.
As a general guideline, only mean sleep latencies shorter than 8 minutes on an MSLT are considered abnormal, and latencies shorter than 5 minutes are taken to indicate severe excessive daytime sleepiness. A patient with a mean sleep latency of 2 minutes or less on an MSLT is unlikely to be exaggerating a complaint of excessive daytime sleepiness, to suffer from fatigue rather than sleepiness, or to be free of any sleep disorder.
As a general guideline, only mean sleep latencies shorter than 8 minutes on an MSLT are considered abnormal, and latencies shorter than 5 minutes are taken to indicate severe excessive daytime sleepiness. A patient with a mean sleep latency of 2 minutes or less on an MSLT is unlikely to be exaggerating a complaint of excessive daytime sleepiness, to suffer from fatigue rather than sleepiness, or to be free of any sleep disorder.
Patient Data
- Ramesh is a 34-year-old man with no major health problems who takes no prescription medicines.
- Sara is a 23-year-old woman with asthma who takes a prescription stimulant daily for treatment.
- Angel is a 72-year-old woman with major depressive disorder who takes a prescription anti-depressant daily.
- John is an 11-year-old child who has been diagnosed with ADD, but does not take any prescription medications.
- Steve is a 54-year-old man with mild heart disease who takes several over-the-counter supplements.
MSLT Results
NOTE: Data given is time until sleep in minutes and seconds. Results may be misleading if they are affected by patient age (different criteria apply for children under 16), noise in the sleep center, patient anxiety during the test, or atypical sleep on the previous night. Use of prescription medications such as stimulants or antidepressants can also lead to misleading results.
Which of the following can be reasonably inferred from the data provided?
a)
John’s MSLT results fall within normal guidelines.
b)
Angel has exaggerated her claim of daytime sleepiness.
c)
Ramesh may suffer from some type of sleep disorder.
d)
John does not suffer from a sleep disorder.
e)
Sara suffers from fatigue, not excessive daytime sleepiness.
|
|
EduRev GMAT answered |
Results for Sara, Angel, and John can be misleading (taking medication, underage)
So, any conclusions for them will not be reliable. Only option C is correct because Ramesh's data is reliable and he is clearly near the 2-minute average mark at which disorders are very likely.
So, any conclusions for them will not be reliable. Only option C is correct because Ramesh's data is reliable and he is clearly near the 2-minute average mark at which disorders are very likely.
If (1 < A < 3 < B), then which of the following expressions is the largest?- a)(B+2)/(A-1)
- b)(B-2)/(A+1)
- c)A/B
- d)(B-2)/(A-1)
- e)B/A
Correct answer is option 'A'. Can you explain this answer?
If (1 < A < 3 < B), then which of the following expressions is the largest?
a)
(B+2)/(A-1)
b)
(B-2)/(A+1)
c)
A/B
d)
(B-2)/(A-1)
e)
B/A
|
|
Mihir Nambiar answered |
The best answer is A.
Try some numbers and check the answers. A=2, B=4.
(a) 6/1 = 6
(b) 2/3
(c) 1/2
(d) 2
(e) 2
Try some numbers and check the answers. A=2, B=4.
(a) 6/1 = 6
(b) 2/3
(c) 1/2
(d) 2
(e) 2
The graph shows the estimated year-end population for the 3 most populous territories in Nation X in 5 selected years. The estimated year-end population of Nation X was 17,000,000 in 1990 and 22,500,000 in 2010.From each drop-down menu, select the option that creates the most accurate statement based on the information provided.
1. The increase in the estimated year-end population of Territory C from 1990 to 2010 accounts for approximately _______ % of the increase in the estimated year-end population of Nation X over the same period.
2. In 2010, the estimated total year-end population of the 3 territories was _______ of the estimated year-end population of Nation X.- a)1: 30
2: Between 70% and 80% - b)1: 20
2: Between 80% and 90% - c)1: 40
2: Between 60% and 70% - d)1: 60
2: Between 50% and 60%
Correct answer is option 'A'. Can you explain this answer?
The graph shows the estimated year-end population for the 3 most populous territories in Nation X in 5 selected years. The estimated year-end population of Nation X was 17,000,000 in 1990 and 22,500,000 in 2010.
From each drop-down menu, select the option that creates the most accurate statement based on the information provided.
1. The increase in the estimated year-end population of Territory C from 1990 to 2010 accounts for approximately _______ % of the increase in the estimated year-end population of Nation X over the same period.
2. In 2010, the estimated total year-end population of the 3 territories was _______ of the estimated year-end population of Nation X.
1. The increase in the estimated year-end population of Territory C from 1990 to 2010 accounts for approximately _______ % of the increase in the estimated year-end population of Nation X over the same period.
2. In 2010, the estimated total year-end population of the 3 territories was _______ of the estimated year-end population of Nation X.
a)
1: 30
2: Between 70% and 80%
2: Between 70% and 80%
b)
1: 20
2: Between 80% and 90%
2: Between 80% and 90%
c)
1: 40
2: Between 60% and 70%
2: Between 60% and 70%
d)
1: 60
2: Between 50% and 60%
2: Between 50% and 60%
|
|
EduRev GMAT answered |
1. Measured in thousands, the estimated year-end population of Territory C was approximately 2,900 in 1990 and 4,600 in 2010, for an increase of approximately 4,600 − 2,900, or 1,700, over that period.
The total estimated year-end population of Nation X, in thousands, was 17,000 in 1990 and 22,500 in 2010, an increase of 22,500 − 17,000, or 5,500.
Thus, Territory C’s population increase represents 100 (1,700/5,500), or 30 10/11, percent of the total increase.
The correct answer is 30.
The total estimated year-end population of Nation X, in thousands, was 17,000 in 1990 and 22,500 in 2010, an increase of 22,500 − 17,000, or 5,500.
Thus, Territory C’s population increase represents 100 (1,700/5,500), or 30 10/11, percent of the total increase.
The correct answer is 30.
2. Measured in thousands, the 2010 estimated year-end population was approximately 7,250 for Territory A, approximately 5,600 for Territory B, and approximately 4,600 for Territory C, for a combined total of approximately 17,450.
The estimated total year-end population, in thousands, of Nation X for 2010 was 22,500.
Thus, the estimated total of the three territories represents 100 (17,450/22,500), or
percent of the estimated year-end total population of Nation X in 2010.
The correct answer is between 70% and 80%.
The estimated total year-end population, in thousands, of Nation X for 2010 was 22,500.
Thus, the estimated total of the three territories represents 100 (17,450/22,500), or
percent of the estimated year-end total population of Nation X in 2010.The correct answer is between 70% and 80%.
Chapter doubts & questions for Day 32 - Daily Tests for GMAT Preparation 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Day 32 - Daily Tests for GMAT Preparation in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup