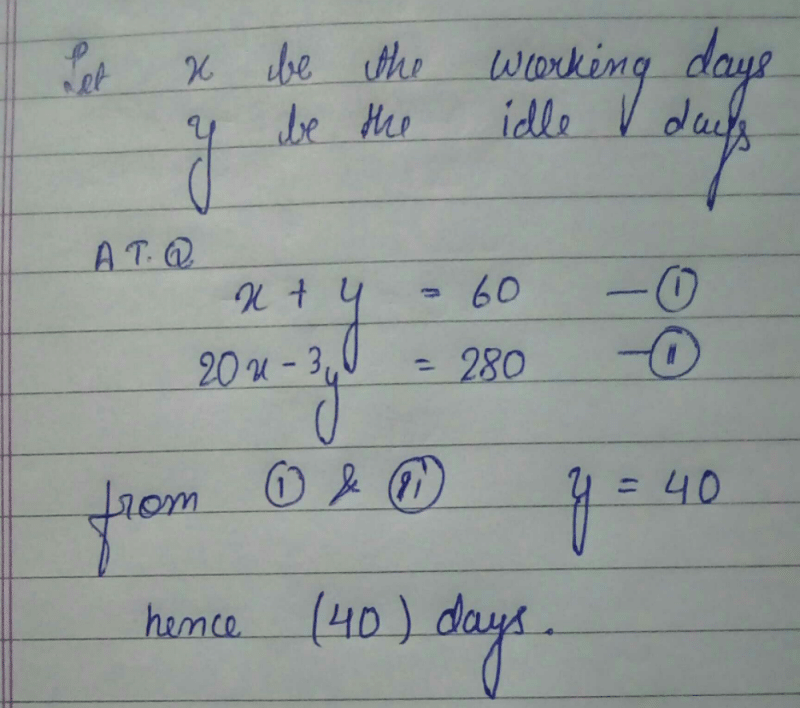All Exams >
CLAT >
4 Months Preparation Course for CLAT UG >
All Questions
All questions of Time And Work for CLAT Exam
A and B can do a work in 8 days B and C in 12 days, C and A in 16 days. All worked for 2 days. How many days willA take to finish the work.
- a)14 days
- b)7 days
- c)
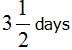
- d)None
- e)All of the above
Correct answer is option 'D'. Can you explain this answer?
A and B can do a work in 8 days B and C in 12 days, C and A in 16 days. All worked for 2 days. How many days willA take to finish the work.
a)
14 days
b)
7 days
c)
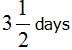
d)
None
e)
All of the above

|
Kunal Singh answered |
According to me answer will be 'd'
A takes twice as much time as B or thrice as much time as C to finish a piece of work; working together they can finish the work in 2 days. In how many days B can do the work alone?
- a)12 days
- b)4 days
- c)8 days
- d)6 days
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A takes twice as much time as B or thrice as much time as C to finish a piece of work; working together they can finish the work in 2 days. In how many days B can do the work alone?
a)
12 days
b)
4 days
c)
8 days
d)
6 days
e)
None of these
|
|
Umang Singh answered |
Let c can finish a piece of work in x days.then a will finish the work in 3x days and b will finish in 1.5x days adding 1 day work of all three we get 1/x+1/3x/1/1.5x= 1/2 we will get x=4 and finally b will finish work in 1.5 ×4 = 6days
A alone can complete a work in 12 days, while A and B together can complete the same work in 8 days. The number of days that B will take to complete the work alone is- a)10 days
- b)24 days
- c)20 days
- d)9 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A alone can complete a work in 12 days, while A and B together can complete the same work in 8 days. The number of days that B will take to complete the work alone is
a)
10 days
b)
24 days
c)
20 days
d)
9 days
e)
None of these

|
Shanaya Sharma answered |
A can complete a work in = 12 days
In 1 day , A can do = 1/12 work
A+B can complete the work in = 8 days
In 1 day , A+B can do = 1/8 work
In 1 day , B can do = 1/8 - 1/12
= 1/24 work
B completes a work in = 24 days
In 1 day , A can do = 1/12 work
A+B can complete the work in = 8 days
In 1 day , A+B can do = 1/8 work
In 1 day , B can do = 1/8 - 1/12
= 1/24 work
B completes a work in = 24 days
A factory produces nuts and bolts. A machine in it produces only nuts while another produces only bolts. The machine producing only nuts produces 500 nuts per minute and need to be cleared for 10 minutes after production of 2000 nuts. The machine producing only bolts produces 600 bolts per minute and needs to be cleared for 15 minutes after production of 3000 bolts. Find the minimum time required to produce 6000 pairs of bolts and nuts if both machines are operated simultaneously.- a)32 minutes
- b)20 minutes
- c)25 minutes
- d)40 minutes
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A factory produces nuts and bolts. A machine in it produces only nuts while another produces only bolts. The machine producing only nuts produces 500 nuts per minute and need to be cleared for 10 minutes after production of 2000 nuts. The machine producing only bolts produces 600 bolts per minute and needs to be cleared for 15 minutes after production of 3000 bolts. Find the minimum time required to produce 6000 pairs of bolts and nuts if both machines are operated simultaneously.
a)
32 minutes
b)
20 minutes
c)
25 minutes
d)
40 minutes
e)
None of these
|
|
Preeti Khanna answered |
2000 nuts are produced in 14 minutes (10 minutes break and 500 nuts per minutes so 4 minutes to produce 2000 nuts ), for next 2000 nuts it will take 14 minutes more, and for more two thousand it will take 4 minutes more, so total time = 32 minutes
similarly, 6000 bolts are produced in 20 + 5 = 25 minutes
so minimum time required is 32 minutes
similarly, 6000 bolts are produced in 20 + 5 = 25 minutes
so minimum time required is 32 minutes
A and B together can do a piece of work in 24 days, which B and C together can do it in 32 days. After A has been working at it for 10 days and B for 14 days, C finishes it in 26 days. In how many days C alone will do the work?- a)32
- b)36
- c)44
- d)48
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A and B together can do a piece of work in 24 days, which B and C together can do it in 32 days. After A has been working at it for 10 days and B for 14 days, C finishes it in 26 days. In how many days C alone will do the work?
a)
32
b)
36
c)
44
d)
48
e)
None of these
|
|
Anaya Patel answered |
Correct Answer :- d
Explanation : Work done by (A+B)'s in 1 day = 24
work done by (B+C)'s in 1 day = 32
Let C does a work in x days
Then work done by C in a day = 1/x
According to the question
A's 10 day's work + B's 14 day's work + C's 26 day's work = 1
10A + 14B + 26C = 1 ;
10A + 10B + 4B + 4C + 22C = 1 ;
10(A + B ) + 4( B + C ) + 22C = 1 ;
10( 1/24 ) + 4( 1/32 ) + 22C = 1 ;
10/24 + 4/32 + 22C = 1 ;
13/24 + 22C = 1 ;
22C = 1 - 13/24 ;
22C = 11/24 ;
2C = 1/24 ;
C = 1/48 ;
Therefore , C alone takes 48 days to finish the job.
A work could be completed in 100 days. Due to the absence of 10 workers it was completed in 110 days. The original number of workers was- a)55
- b)100
- c)50
- d)110
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A work could be completed in 100 days. Due to the absence of 10 workers it was completed in 110 days. The original number of workers was
a)
55
b)
100
c)
50
d)
110
e)
None of these

|
Ishani Rane answered |
Originally let there be x men.
Less men, More days (Indirect Proportion)
Therefore, (x-10) : x :: 100 :110
=> (x - 10) * 110 = x * 100 => x= 110
A piece of work can be done by 6 men and 5 women in 6 days or 3 men and 4 women in 10 days. It can be done by 9 men and 15 women in how many days ?- a)3 days
- b)4 days
- c)5 days
- d)6 days
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A piece of work can be done by 6 men and 5 women in 6 days or 3 men and 4 women in 10 days. It can be done by 9 men and 15 women in how many days ?
a)
3 days
b)
4 days
c)
5 days
d)
6 days
e)
None of these

|
Avantika Chakraborty answered |
To calculate the answer we need to get 1 man per day work and 1 woman per day work.
Let 1 man 1 day work =x
and 1 woman 1 days work = y.
=> 6x+5y = 1/6
and 3x+4y = 1/10
On solving, we get x = 1/54 and y = 1/90
(9 men + 15 women)'s 1 days work =
(9/54) + (15/90) = 1/3
9 men and 15 women will finish the work in 3 days
If P and Q work together, they will complete a job in 7.5 days. However, if P works alone and completes half the job and then Q takes over and completes the remaining half alone, they will be able to complete the job in 20 days. How long will Q alone take to do the job if P is more efficient than Q?- a)20 days
- b)30 days
- c)40 days
- d)10 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If P and Q work together, they will complete a job in 7.5 days. However, if P works alone and completes half the job and then Q takes over and completes the remaining half alone, they will be able to complete the job in 20 days. How long will Q alone take to do the job if P is more efficient than Q?
a)
20 days
b)
30 days
c)
40 days
d)
10 days
e)
None of these

|
Naroj Boda answered |
1/P + 1/Q = 2/15 from first line. Now, let P take x days and Q takes y days to complete half the work respectively.
x/P = 1/2, x = P/2 similarly y/Q = 1/2, y = Q/2
so, x +y = 20 i.e. P/2 + Q/2 = 20, P +Q = 40
solve both equation, u will get Q = 30 days
x/P = 1/2, x = P/2 similarly y/Q = 1/2, y = Q/2
so, x +y = 20 i.e. P/2 + Q/2 = 20, P +Q = 40
solve both equation, u will get Q = 30 days
A piece of work has to be completed in 50 days, a number of men are employed but it is found that only half of the work is done in 30 days, then an additional 20 men were joined to complete the work on time. How many men initially put to work?- a)30
- b)35
- c)40
- d)45
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A piece of work has to be completed in 50 days, a number of men are employed but it is found that only half of the work is done in 30 days, then an additional 20 men were joined to complete the work on time. How many men initially put to work?
a)
30
b)
35
c)
40
d)
45
e)
None of these

|
KS Coaching Center answered |
suppose Initially X men get employed. Half work is done in 30 days it means full work will be done by X men in 60 days. Now,
Work done = 1/2 = [20*(x + 20)]/60X
X = 40
Work done = 1/2 = [20*(x + 20)]/60X
X = 40
If P can do 1/3 of the work in 5 days and Q can do 1/4 of the work in 6 days, then how much money will Q get if they were paid a total of 390 rupee?- a)120
- b)150
- c)170
- d)190
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If P can do 1/3 of the work in 5 days and Q can do 1/4 of the work in 6 days, then how much money will Q get if they were paid a total of 390 rupee?
a)
120
b)
150
c)
170
d)
190
e)
None of these

|
Bank Exams India answered |
sol = P can alone complete the whole work in 15 days and Q can complete the same work alone in 24 days. So ratio of work done by them 1/15: 1/24 i.e. 8: 5
Q get = (5/13)*390 = 150
Q get = (5/13)*390 = 150
Among four persons Anuj, Bhim, Carl and Dinesh. Anuj takes thrice as much time as Bhim to complete a piece of work. Bhim takes thrice as much time as Carl and Carl takes thrice as much time as Dinesh to complete the same work. If all together they take 3 days to complete the work. Find the time taken by Bhim alone to complete the work alone.- a)20 days
- b)30 days
- c)40 days
- d)50 days
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Among four persons Anuj, Bhim, Carl and Dinesh. Anuj takes thrice as much time as Bhim to complete a piece of work. Bhim takes thrice as much time as Carl and Carl takes thrice as much time as Dinesh to complete the same work. If all together they take 3 days to complete the work. Find the time taken by Bhim alone to complete the work alone.
a)
20 days
b)
30 days
c)
40 days
d)
50 days
e)
None of these
|
|
Faizan Khan answered |
Let Bhim takes x days alone to complete the job, so Anuj will take 3x days, Carl will take x/3 days and Dinesh will take x/9 days to complete the work alone
1/3x + 1/x + 3/x + 9/x = 1/3
Solve for x
1/3x + 1/x + 3/x + 9/x = 1/3
Solve for x
A, B and C together earn Rs. 150 per day while A & C together earn Rs. 94 and B and C together earn Rs. 76. The daily earning of C is:- a)Rs. 75
- b)Rs. 56
- c)Rs. 34
- d)Rs. 20
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A, B and C together earn Rs. 150 per day while A & C together earn Rs. 94 and B and C together earn Rs. 76. The daily earning of C is:
a)
Rs. 75
b)
Rs. 56
c)
Rs. 34
d)
Rs. 20
e)
None of these
|
|
Sagar Sharma answered |
To solve this problem, we can use a system of equations. Let's assign variables to the daily earnings of A, B, and C.
Let A's daily earning be x, B's daily earning be y, and C's daily earning be z.
According to the given information, A, B, and C together earn Rs. 150 per day. So we can write the equation:
x + y + z = 150
We are also given that A + C together earn Rs. 94, so we can write the equation:
x + z = 94
Similarly, B + C together earn Rs. 76, so we can write the equation:
y + z = 76
Now we have a system of three equations with three variables. We can solve this system to find the value of z, which represents C's daily earnings.
We can solve this system by substitution or elimination. Let's use elimination:
First, let's subtract the second equation from the first equation to eliminate z:
(x + y + z) - (x + z) = 150 - 94
Simplifying, we get:
y = 56
Now we have the value of y.
Next, let's subtract the third equation from the first equation to eliminate z:
(x + y + z) - (y + z) = 150 - 76
Simplifying, we get:
x = 74
Now we have the value of x.
Finally, we can substitute the values of x and y into the second equation to solve for z:
74 + z = 94
Subtracting 74 from both sides, we get:
z = 20
Therefore, C's daily earnings are Rs. 20.
Hence, the correct answer is option D) Rs. 20.
Let A's daily earning be x, B's daily earning be y, and C's daily earning be z.
According to the given information, A, B, and C together earn Rs. 150 per day. So we can write the equation:
x + y + z = 150
We are also given that A + C together earn Rs. 94, so we can write the equation:
x + z = 94
Similarly, B + C together earn Rs. 76, so we can write the equation:
y + z = 76
Now we have a system of three equations with three variables. We can solve this system to find the value of z, which represents C's daily earnings.
We can solve this system by substitution or elimination. Let's use elimination:
First, let's subtract the second equation from the first equation to eliminate z:
(x + y + z) - (x + z) = 150 - 94
Simplifying, we get:
y = 56
Now we have the value of y.
Next, let's subtract the third equation from the first equation to eliminate z:
(x + y + z) - (y + z) = 150 - 76
Simplifying, we get:
x = 74
Now we have the value of x.
Finally, we can substitute the values of x and y into the second equation to solve for z:
74 + z = 94
Subtracting 74 from both sides, we get:
z = 20
Therefore, C's daily earnings are Rs. 20.
Hence, the correct answer is option D) Rs. 20.
A can do a piece of work in 12 hours and with the help of his son, he is able to do it in 8 hours. How many hours will the son alone take to finish the work?
- a)20 hours
- b)24 hours
- c)4 hours
- d)None
- e)All of the above
Correct answer is option 'B'. Can you explain this answer?
A can do a piece of work in 12 hours and with the help of his son, he is able to do it in 8 hours. How many hours will the son alone take to finish the work?
a)
20 hours
b)
24 hours
c)
4 hours
d)
None
e)
All of the above
|
|
Kavya Saxena answered |
Correct Answer :- b
Explanation : M can do 1/12 work in a day.
M and S altogether will do 1/8 work in a day.
Work of M in a day + Work of S in a day
1/M + 1/S = 1/8
1/12 + 1/S = 1/8
1/S = 1/8 – 1/12
1/S = 1/24
S = 24
That means S in one day can do 24 work
8 men can do a work in 12 days. After 6 days of work four more men were employed. In how many days would the remaining work be done. - a)2 days
- b)3 days
- c)4 days
- d)5 days
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
8 men can do a work in 12 days. After 6 days of work four more men were employed. In how many days would the remaining work be done.
a)
2 days
b)
3 days
c)
4 days
d)
5 days
e)
None of these

|
Kavya Sharma answered |
Description for Correct answer:
let 1 men does 1 unit of work per day
Total work: 8x12=96units
6 days work of 8 men
=8x6=48 units.
work lelt =96−48=48 units
After 6 days 4 men join. so total men is 12 men (8+4) they will do 12 unit of work per day
Now,
remaining work completed in
=48/12
= 4 days
A is twice as good a workman as B and together they finish a piece of work in 14 days. A alone can finish the work in- a)11 days
- b)21 days
- c)28 days
- d)42 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A is twice as good a workman as B and together they finish a piece of work in 14 days. A alone can finish the work in
a)
11 days
b)
21 days
c)
28 days
d)
42 days
e)
None of these
|
|
Kendrika answered |
If time taken by B be 2x days then time taken by A = x days.
∴ 1/x+1/2x = 1/14
=2+1/2x = 1/14
= 3x = 1/7
= x = 1/ 3 ×7 = 1/21
= 21 days
∴ 1/x+1/2x = 1/14
=2+1/2x = 1/14
= 3x = 1/7
= x = 1/ 3 ×7 = 1/21
= 21 days
A does half as much work as B does in one sixth of the time. If together they take 20 days to complete the work, then what is the time taken by A to complete the work independently.- a)80/3 days
- b)100/3 days
- c)60/3 days
- d)140/3 days
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A does half as much work as B does in one sixth of the time. If together they take 20 days to complete the work, then what is the time taken by A to complete the work independently.
a)
80/3 days
b)
100/3 days
c)
60/3 days
d)
140/3 days
e)
None of these
|
|
Faizan Khan answered |
Let B complete the work in X days so in one day work done by B is 1/x
as A do half work in one-sixth of the time so A will complete work in 2*x/6 = x/3 days
One day work of A and B i.e. 3/x + 1/x = 1/20. So we get x = 80
So time taken by A alone = 80/3 days
as A do half work in one-sixth of the time so A will complete work in 2*x/6 = x/3 days
One day work of A and B i.e. 3/x + 1/x = 1/20. So we get x = 80
So time taken by A alone = 80/3 days
Ram and shyam can do a piece of work in 5 and 7 days respectively. They start working alternatively starting from shyam, then in how many days the work is completed- a)5.(3/7) days
- b)6.(5/7) days
- c)7.(5/6) days
- d)5.(6/7) days
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Ram and shyam can do a piece of work in 5 and 7 days respectively. They start working alternatively starting from shyam, then in how many days the work is completed
a)
5.(3/7) days
b)
6.(5/7) days
c)
7.(5/6) days
d)
5.(6/7) days
e)
None of these
|
|
Alok Verma answered |
1/7 + 1/5 = 12/35 this much work is completed in 2 days.
So 24/35 will be completed in 4 days
In the next day, 29/35 work get completed in 5 days, so remaining work will be completed by Ram in 6/7 days
So 24/35 will be completed in 4 days
In the next day, 29/35 work get completed in 5 days, so remaining work will be completed by Ram in 6/7 days
A and B can together finish a work 30 days. They worked together for 20 days and then B left. After another 20 days, A finished the remaining work. In how many days A alone can finish the work?- a)70 days
- b)60 days
- c)12 days
- d)65 days
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
A and B can together finish a work 30 days. They worked together for 20 days and then B left. After another 20 days, A finished the remaining work. In how many days A alone can finish the work?
a)
70 days
b)
60 days
c)
12 days
d)
65 days
e)
None of the above
|
|
Yash Patel answered |
(A + B)'s 20day's work
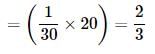
Remaining work

Now,  work is done by A in 20 days
work is done by A in 20 days
 work is done by A in 20 days
work is done by A in 20 days∴ The whole work will be done by A in (20×3) = 60days
If 12 men and 16 boys can do a piece work in 5 days, 13 men and 24 boys can do it in four days then the ratio of the work done daily by a man and a boy is?- a)3 : 1
- b)2 : 1
- c)5 : 4
- d)4 : 5
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If 12 men and 16 boys can do a piece work in 5 days, 13 men and 24 boys can do it in four days then the ratio of the work done daily by a man and a boy is?
a)
3 : 1
b)
2 : 1
c)
5 : 4
d)
4 : 5
e)
None of these
|
|
Arya Gaddam answered |
Let's consider
x=men and y=boys
by first condition,
12x+16y=1/5
by second condition,
13x+24y=1/4
by solving them we get
x=1/100 and y=1/200
so x:y=2:1
x=men and y=boys
by first condition,
12x+16y=1/5
by second condition,
13x+24y=1/4
by solving them we get
x=1/100 and y=1/200
so x:y=2:1
72 men can build a wall 280 m long in 21 days. How many men will take 18 days to build a similar type of a wall of length 100 m.- a)28
- b)18
- c)10
- d)30
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
72 men can build a wall 280 m long in 21 days. How many men will take 18 days to build a similar type of a wall of length 100 m.
a)
28
b)
18
c)
10
d)
30
e)
None of these

|
Kavya Sharma answered |
Here work is 280 m length of wall and 100 m length of wall,
Let 'M' men will finish 100 m wall.
72x21/280=Mx18/100
M=30
A group of 24 women is supposed to do a work in 40 days. After 20 days 4 more women is employed and the work is completed in 2 days before the scheduled time. How many days it have been delayed if 4 more women were not employed?- a)1 day
- b)2 day
- c)3 day
- d)4 day
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A group of 24 women is supposed to do a work in 40 days. After 20 days 4 more women is employed and the work is completed in 2 days before the scheduled time. How many days it have been delayed if 4 more women were not employed?
a)
1 day
b)
2 day
c)
3 day
d)
4 day
e)
None of these
|
|
Anaya Patel answered |
24*20 + 28*18 = total work = 24*T (T is the number of days when 4 more women are not employed)
we get T = 41, so work will be delayed by 1 day
we get T = 41, so work will be delayed by 1 day
A and B can do a piece of work in 20 and 25 days respectively. They began to work together but A leaves after some days and B completed the remaining work in 12 days. Number of days after which A left the job
- a)52/9 days
- b)67/9 days
- c)77/9 days
- d)117/9 days
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A and B can do a piece of work in 20 and 25 days respectively. They began to work together but A leaves after some days and B completed the remaining work in 12 days. Number of days after which A left the job
a)
52/9 days
b)
67/9 days
c)
77/9 days
d)
117/9 days
e)
None of these
|
|
Ravi Singh answered |
(1/20 + 1/25)*T + 12/25 = 1
We will get T = 52/9 days
We will get T = 52/9 days
P can do a piece of work in 20 days. Q is 25 percent more efficient than P. In how many days half the work is completed when both are working simultaneously?- a)41/9
- b)40/9
- c)39/9
- d)43/9
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
P can do a piece of work in 20 days. Q is 25 percent more efficient than P. In how many days half the work is completed when both are working simultaneously?
a)
41/9
b)
40/9
c)
39/9
d)
43/9
e)
None of these
|
|
Aisha Gupta answered |
Q is 25 percent more efficient so he will complete the work in 16 days
(1/20 + 1/16)*t = 1/2
(1/20 + 1/16)*t = 1/2
P and Q can do a piece of work in 10 days and 20 days respectively. Both of them start the work but P leaves the work 5 days before its completion. Find the time in which work is completed- a)10
- b)15
- c)20
- d)25
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
P and Q can do a piece of work in 10 days and 20 days respectively. Both of them start the work but P leaves the work 5 days before its completion. Find the time in which work is completed
a)
10
b)
15
c)
20
d)
25
e)
None of these
|
|
Alok Verma answered |
(1/10 + 1/20)*(T-5) + 5/20 = 1 (T is the number of days in which the work is completed)
50 men could complete a work in 200 days. They worked together for 150 days, after that due to bad weather the work is stopped for 25 days. How many more workers should be employed so as to complete the work in time?- a)25
- b)35
- c)50
- d)60
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
50 men could complete a work in 200 days. They worked together for 150 days, after that due to bad weather the work is stopped for 25 days. How many more workers should be employed so as to complete the work in time?
a)
25
b)
35
c)
50
d)
60
e)
None of these
|
|
Ravi Singh answered |
Let additional workers be P, (50*150)/(50*200) = 3/4 of the work is already completed and now only 1/4 of the work is to be done. So,
1/4 = ((50 + P) * 25)/50*200, solve for p, we get P = 50
1/4 = ((50 + P) * 25)/50*200, solve for p, we get P = 50
A is thrice as good as workman as B and takes 10 days less to do a piece of work than B takes. B can do the work in- a)12 days
- b)15 days
- c)20 days
- d)30 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A is thrice as good as workman as B and takes 10 days less to do a piece of work than B takes. B can do the work in
a)
12 days
b)
15 days
c)
20 days
d)
30 days
e)
None of these
|
|
Kendrika answered |
Ratio of times taken by A and B = 1:3
Means B will take 3 times which A will do in 1 time
If difference of time is 2 days, B takes 3 days
If difference of time is 10 days, B takes (3/2) * 10 =15 days
Means B will take 3 times which A will do in 1 time
If difference of time is 2 days, B takes 3 days
If difference of time is 10 days, B takes (3/2) * 10 =15 days
Three professors P, Q, R are evaluating answer script of a subject. P is 40 more efficient than Q, who is 20 more efficient than R. P takes 10 days less than Q to complete the evaluation work. P starts the evaluation work and works for 10 days and then Q takes over. Q evaluates for next 15 days and then stops. In how many days, R can complete the remaining evaluation work?- a)6.2 days
- b)7.2 days
- c)8.2 days
- d)9.2 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Three professors P, Q, R are evaluating answer script of a subject. P is 40 more efficient than Q, who is 20 more efficient than R. P takes 10 days less than Q to complete the evaluation work. P starts the evaluation work and works for 10 days and then Q takes over. Q evaluates for next 15 days and then stops. In how many days, R can complete the remaining evaluation work?
a)
6.2 days
b)
7.2 days
c)
8.2 days
d)
9.2 days
e)
None of these

|
KS Coaching Center answered |
Let R takes x days to complete the work, then
1/P = (140/100)*1/Q and 1/Q = (120/100)*1/R
So P will take 25x/42 and Q will take 5x/6 days respectively
5x/6 – 25x/42 = 10, we get x = 42
10/25 + 15/35 + t/42 = 1
1/P = (140/100)*1/Q and 1/Q = (120/100)*1/R
So P will take 25x/42 and Q will take 5x/6 days respectively
5x/6 – 25x/42 = 10, we get x = 42
10/25 + 15/35 + t/42 = 1
Sunil completes a work in 4 days whereas Hrithik completes the work in 6 days. Ramesh work 1 ½ times as fast as Sunil. How many days it will take for the three together the complete the work?- a)7/12
- b)15/12
- c)15/7
- d)16/7
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
Sunil completes a work in 4 days whereas Hrithik completes the work in 6 days. Ramesh work 1 ½ times as fast as Sunil. How many days it will take for the three together the complete the work?
a)
7/12
b)
15/12
c)
15/7
d)
16/7
e)
None of these

|
Tanvi Dey answered |
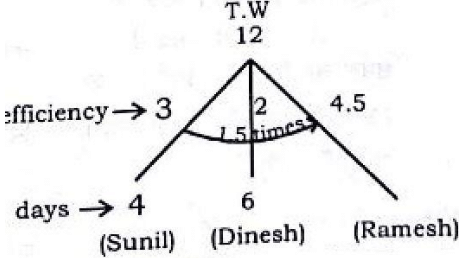
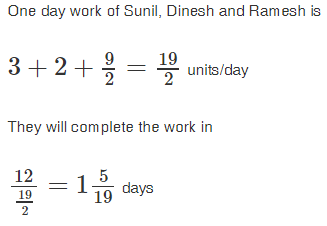
Mahesh and Umesh can complete a work in 10 days and 15 days respectively. Umesh starts the work and after 5 days Mahesh also joins him. In all, the work would be completed in- a)7 days
- b)9 days
- c)11 days
- d)12 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Mahesh and Umesh can complete a work in 10 days and 15 days respectively. Umesh starts the work and after 5 days Mahesh also joins him. In all, the work would be completed in
a)
7 days
b)
9 days
c)
11 days
d)
12 days
e)
None of these
|
|
Naman Agrawal answered |
Umesh 5 days work =5/15;
remaining work =1-1/3=2/3;
together 1 day work of Mahesh and Umesh = 1/15+1/10= 1/6;
so, they will do together 2/3 of work in =(2/3)/+(1/6) =4 days.
hence, the work was completed in (4+5) =9 days. op(b)
remaining work =1-1/3=2/3;
together 1 day work of Mahesh and Umesh = 1/15+1/10= 1/6;
so, they will do together 2/3 of work in =(2/3)/+(1/6) =4 days.
hence, the work was completed in (4+5) =9 days. op(b)
P can do a piece of work in 20 days. Q is 25 percent more efficient than P. In how many days half the work is completed when both are working simultaneously?- a)41/9
- b)40/9
- c)39/9
- d)43/9
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
P can do a piece of work in 20 days. Q is 25 percent more efficient than P. In how many days half the work is completed when both are working simultaneously?
a)
41/9
b)
40/9
c)
39/9
d)
43/9
e)
None of these
|
|
Rajeev Kumar answered |
Q is 25 percent more efficient so he will complete the work in 16 days
(1/20 + 1/16)*t = 1/2
(1/20 + 1/16)*t = 1/2
A and B can together finish a work in 30 days. They worked for it for 20 days and then B left. The remaining work done by A alone in 20 more days. A alone can finish the work in- a)48 days
- b)50 days
- c)54 days
- d)60 days
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A and B can together finish a work in 30 days. They worked for it for 20 days and then B left. The remaining work done by A alone in 20 more days. A alone can finish the work in
a)
48 days
b)
50 days
c)
54 days
d)
60 days
e)
None of these
|
|
Sajal Bdw answered |
Amount of work done in 1 day = 1/30
Amount of work done in 20 days = 20 * (1/30) = 2/3
Remaining work = 1 - 2/3 = 1/3
Given, A completes 1/3 work in 20 days.
Therefore, A can finish the whole work in (20 x 3) = 60 days.
HENCE OPTION D IS THE ANSWER
Amount of work done in 20 days = 20 * (1/30) = 2/3
Remaining work = 1 - 2/3 = 1/3
Given, A completes 1/3 work in 20 days.
Therefore, A can finish the whole work in (20 x 3) = 60 days.
HENCE OPTION D IS THE ANSWER
A and B undertake to complete a piece of work for Rupees 1200. A can do it in 8 days, B can do it in 12 days and with the help of C they complete the work in 4 days. Find the share of C?- a)100
- b)200
- c)300
- d)400
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A and B undertake to complete a piece of work for Rupees 1200. A can do it in 8 days, B can do it in 12 days and with the help of C they complete the work in 4 days. Find the share of C?
a)
100
b)
200
c)
300
d)
400
e)
None of these
|
|
Alok Verma answered |
1/8 + 1/12 + 1/C = 1/4, we get C = 24 days
now efficiency of A, B and C are in the ratio of 1/8 :1/12 : 1/24
3:2:1, so share of C is 1/6 * 1200 = 200
now efficiency of A, B and C are in the ratio of 1/8 :1/12 : 1/24
3:2:1, so share of C is 1/6 * 1200 = 200
A can do a piece of work in 25 days and B in 75 days. Working together, In how many days will they complete the work.- a)
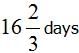
- b)

- c)
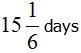
- d)None
- e)All of the above
Correct answer is option 'B'. Can you explain this answer?
A can do a piece of work in 25 days and B in 75 days. Working together, In how many days will they complete the work.
a)
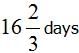
b)

c)
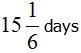
d)
None
e)
All of the above
|
|
Nishtha Pandey answered |
A's one day work= 1/25
B's one day work= 1/75
(A+B)'s one day work= 1/25+1/75=4/75
together, completion of work=75/4 or 18 3/4days.
B's one day work= 1/75
(A+B)'s one day work= 1/25+1/75=4/75
together, completion of work=75/4 or 18 3/4days.
A and B can do a piece of work in 4 days, B and C in 6 days and A, B and C all together in 3 days, what time will A and C take to do it?- a)4 days
- b)8 days
- c)12 days
- d)None
- e)All of the above
Correct answer is option 'A'. Can you explain this answer?
A and B can do a piece of work in 4 days, B and C in 6 days and A, B and C all together in 3 days, what time will A and C take to do it?
a)
4 days
b)
8 days
c)
12 days
d)
None
e)
All of the above
|
|
Nishtha Pandey answered |
(A+B)'s one day work= 1/4
(B+C)'s one day work= 1/6
(A+B+C)'s one day work= 1/3
(A+C)'s one day work=?
now,
(A+B)'s one day work+C's one day work=1/3
1/4+C's one day work=1/3
C's one day work=1/12
A's one day work+(B+C)'s one day work=1/3
A's one day work+1/6=1/3
A's one day work= 1/6
so,
(A+C)'s one day work= 1/12+1/6=3/12=1/4
both together will take 4days to complete the work.
(B+C)'s one day work= 1/6
(A+B+C)'s one day work= 1/3
(A+C)'s one day work=?
now,
(A+B)'s one day work+C's one day work=1/3
1/4+C's one day work=1/3
C's one day work=1/12
A's one day work+(B+C)'s one day work=1/3
A's one day work+1/6=1/3
A's one day work= 1/6
so,
(A+C)'s one day work= 1/12+1/6=3/12=1/4
both together will take 4days to complete the work.
Twelve men can complete a work in 8 days. Three days after they started the work, 3 more men joined them. In how many days will all of them together complete the remaining work:- a)2
- b)4
- c)5
- d)6
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Twelve men can complete a work in 8 days. Three days after they started the work, 3 more men joined them. In how many days will all of them together complete the remaining work:
a)
2
b)
4
c)
5
d)
6
e)
None of these

|
Chahat Goyal answered |
Total work= 12×8 =96
together they work for 3 days, then 3×12=36
remaining work= 96- 36=60
now 3 more men join them, total workers =15
time taken to complete the remaining work=60/15= 4
Hence, correct option is 'B'.
together they work for 3 days, then 3×12=36
remaining work= 96- 36=60
now 3 more men join them, total workers =15
time taken to complete the remaining work=60/15= 4
Hence, correct option is 'B'.
A piece of work has to be completed in 50 days, a number of men are employed but it is found that only half of the work is done in 30 days, then an additional 20 men were joined to complete the work on time. How many men initially put to work?- a)30
- b)35
- c)40
- d)45
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A piece of work has to be completed in 50 days, a number of men are employed but it is found that only half of the work is done in 30 days, then an additional 20 men were joined to complete the work on time. How many men initially put to work?
a)
30
b)
35
c)
40
d)
45
e)
None of these
|
|
Nikita Singh answered |
suppose Initially X men get employed. Half work is done in 30 days it means full work will be done by X men in 60 days. Now,
Work done = 1/2 = [20*(x + 20)]/60X
X = 40
Work done = 1/2 = [20*(x + 20)]/60X
X = 40
A does half as much work as B in one third of the time taken by B. If together they take 20 days to finish the work then what will be the share of A if 1000 rupees is given for the whole work?- a)400
- b)500
- c)600
- d)700
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A does half as much work as B in one third of the time taken by B. If together they take 20 days to finish the work then what will be the share of A if 1000 rupees is given for the whole work?
a)
400
b)
500
c)
600
d)
700
e)
None of these
|
|
Aarav Sharma answered |
Given:
- A does half as much work as B
- A takes one-third of the time taken by B
Let's assume that B takes 'x' days to complete the work. Therefore, A takes '2x' days to complete the work.
Since A and B together take 20 days to finish the work, we can write the equation:
1/x + 1/2x = 1/20
Solving this equation, we get:
2 + 1 = x/20
3 = x/20
x = 60
So, B takes 60 days to complete the work, and A takes 2x = 120 days to complete the work.
Now, to find the share of A if 1000 rupees is given for the whole work:
The share of A is directly proportional to the amount of work done by A.
The amount of work done by A is given by:
Work done by A = (1/2) * Total work
Total work = 1000 rupees
Therefore, the share of A = (1/2) * 1000 = 500 rupees.
Hence, the correct answer is option 'C' - 600.
- A does half as much work as B
- A takes one-third of the time taken by B
Let's assume that B takes 'x' days to complete the work. Therefore, A takes '2x' days to complete the work.
Since A and B together take 20 days to finish the work, we can write the equation:
1/x + 1/2x = 1/20
Solving this equation, we get:
2 + 1 = x/20
3 = x/20
x = 60
So, B takes 60 days to complete the work, and A takes 2x = 120 days to complete the work.
Now, to find the share of A if 1000 rupees is given for the whole work:
The share of A is directly proportional to the amount of work done by A.
The amount of work done by A is given by:
Work done by A = (1/2) * Total work
Total work = 1000 rupees
Therefore, the share of A = (1/2) * 1000 = 500 rupees.
Hence, the correct answer is option 'C' - 600.
A and B can do a work in 12 days, B and C in 15 days, C and A in 20 days. A alone can do the work in- a)60 days
- b)30 days
- c)20 days
- d)6 days
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A and B can do a work in 12 days, B and C in 15 days, C and A in 20 days. A alone can do the work in
a)
60 days
b)
30 days
c)
20 days
d)
6 days
e)
None of these

|
Ollivia X answered |
A+B 1day work= 1/12. B+C 1day work= 1/15.
C+A 1day work = 1/20.
1 day work of(A+B+C)= (1/12 +1/15+1/20)÷2 = 1/10.
A's 1 day work = 1day work of (A+B+C) - 1day work of (B+C)
= 1/10 - 1/15
= 1/30.
so, A will alone take 30 days yo do the work.
C+A 1day work = 1/20.
1 day work of(A+B+C)= (1/12 +1/15+1/20)÷2 = 1/10.
A's 1 day work = 1day work of (A+B+C) - 1day work of (B+C)
= 1/10 - 1/15
= 1/30.
so, A will alone take 30 days yo do the work.
P, Q and R can do a piece of work in 16, 24 and 30 days respectively. They started the work simultaneously but P stops the work after 4 days and Q called off the work 2 days before the completion. In what time the work is finished?- a)100/9 days
- b)100/11 days
- c)100/7 days
- d)100/13 days
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
P, Q and R can do a piece of work in 16, 24 and 30 days respectively. They started the work simultaneously but P stops the work after 4 days and Q called off the work 2 days before the completion. In what time the work is finished?
a)
100/9 days
b)
100/11 days
c)
100/7 days
d)
100/13 days
e)
None of these
|
|
Aarav Sharma answered |
To find the time taken to complete the work, we need to calculate the work done per day by each person.
Let's denote the work done by P, Q, and R per day as Pd, Qd, and Rd respectively.
Given:
P completes the work in 16 days, so Pd = 1/16 (as 1 work is done in 16 days)
Q completes the work in 24 days, so Qd = 1/24 (as 1 work is done in 24 days)
R completes the work in 30 days, so Rd = 1/30 (as 1 work is done in 30 days)
Let's assume the total work to be done is 1 unit.
Work done by P in 4 days = Pd * 4 = (1/16) * 4 = 1/4
Remaining work = 1 - 1/4 = 3/4
Now, Q called off the work 2 days before completion, which means Q worked for (24 - 2) = 22 days.
Work done by Q in 22 days = Qd * 22 = (1/24) * 22 = 11/12
Remaining work = 3/4 - 11/12 = 9/12 - 11/12 = -2/12 = -1/6
The negative value indicates that the work is already completed before Q called off the work.
Since R was working until the completion of the work, R worked for a total of 30 days.
Work done by R in 30 days = Rd * 30 = (1/30) * 30 = 1
Therefore, the work is already completed when Q called off the work.
The remaining work is negative, indicating that the work is already finished.
Hence, the work is finished in 22 days.
Therefore, the correct answer is option A) 100/9 days.
Let's denote the work done by P, Q, and R per day as Pd, Qd, and Rd respectively.
Given:
P completes the work in 16 days, so Pd = 1/16 (as 1 work is done in 16 days)
Q completes the work in 24 days, so Qd = 1/24 (as 1 work is done in 24 days)
R completes the work in 30 days, so Rd = 1/30 (as 1 work is done in 30 days)
Let's assume the total work to be done is 1 unit.
Work done by P in 4 days = Pd * 4 = (1/16) * 4 = 1/4
Remaining work = 1 - 1/4 = 3/4
Now, Q called off the work 2 days before completion, which means Q worked for (24 - 2) = 22 days.
Work done by Q in 22 days = Qd * 22 = (1/24) * 22 = 11/12
Remaining work = 3/4 - 11/12 = 9/12 - 11/12 = -2/12 = -1/6
The negative value indicates that the work is already completed before Q called off the work.
Since R was working until the completion of the work, R worked for a total of 30 days.
Work done by R in 30 days = Rd * 30 = (1/30) * 30 = 1
Therefore, the work is already completed when Q called off the work.
The remaining work is negative, indicating that the work is already finished.
Hence, the work is finished in 22 days.
Therefore, the correct answer is option A) 100/9 days.
4 men and 6 women can complete a work in 8 days while 3 men and 7 women can complete it in 10 days. In how many days will 10 women complete the work.- a)50
- b)45
- c)40
- d)35
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
4 men and 6 women can complete a work in 8 days while 3 men and 7 women can complete it in 10 days. In how many days will 10 women complete the work.
a)
50
b)
45
c)
40
d)
35
e)
None of these

|
Prerna Sen answered |
Let 1 man's 1 day's work = x and 1 woman's 1 day's work = y.
Then, 4x + 6y = 1/8
and 3x + 7y = 1/10
Solving the two equations, we get: x = 11/400, y = 1/400
1 woman's 1 day's work = 1/400
10 women's 1 day's work = (1/400)*10 = 1/40
Hence, 10 women will complete the work in 40 days
A and B can do a piece of work in 24 and 30 days respectively. Both started the work and worked for 6 days. Then B leaves the work and C joins and the remaining work is completed by A and C together in 11 days. Find the days in which C alone can do the work- a)80
- b)100
- c)120
- d)130
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A and B can do a piece of work in 24 and 30 days respectively. Both started the work and worked for 6 days. Then B leaves the work and C joins and the remaining work is completed by A and C together in 11 days. Find the days in which C alone can do the work
a)
80
b)
100
c)
120
d)
130
e)
None of these
|
|
Kavya Saxena answered |
(1/24 + 1/30)*6 + (1/24 + 1/c)*11 = 1
A works twice as fast as B. if both of them can together finish a work in 12 days, B alone can do it in.- a)40 days
- b)27 days
- c)36 days
- d)24 days
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A works twice as fast as B. if both of them can together finish a work in 12 days, B alone can do it in.
a)
40 days
b)
27 days
c)
36 days
d)
24 days
e)
None of these

|
Jahanvi Kumari answered |
Let time taken by b to do the work=2t
:a= t
1 day work of a and b = 1/2t+1/t=1+2/2t
=3/2t_(1)
1day work of a and b =1/12_(2)
1/12=3/2t
t=18
b can do that work alone =18×2=36
:a= t
1 day work of a and b = 1/2t+1/t=1+2/2t
=3/2t_(1)
1day work of a and b =1/12_(2)
1/12=3/2t
t=18
b can do that work alone =18×2=36
A can finish a work in 24 days, B in 9 days and C in 12 days. B and C start the work but are forced to leave after 3 days. The remaining work was done by A in:
- a)6 days
- b)9 days
- c)10 days
- d)13 days
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A can finish a work in 24 days, B in 9 days and C in 12 days. B and C start the work but are forced to leave after 3 days. The remaining work was done by A in: |
a)
6 days
b)
9 days
c)
10 days
d)
13 days
e)
None of these

|
Bijoy Pillai answered |
Correct Option is (C)
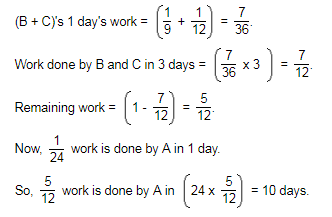
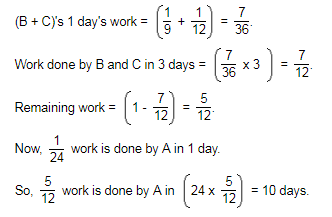
A tank is filled by a pipeA in 32 min. and pipe B in 36 min. When filled, it can be emptied by pipe C in 20 minute. If all the three pipes are opened simultaneously 1/3rd of tank will be filled in- a)
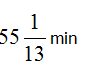
- b)
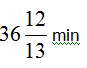
- c)
- d)None
- e)All of the above
Correct answer is option 'B'. Can you explain this answer?
A tank is filled by a pipeA in 32 min. and pipe B in 36 min. When filled, it can be emptied by pipe C in 20 minute. If all the three pipes are opened simultaneously 1/3rd of tank will be filled in
a)
b)
c)
d)
None
e)
All of the above
|
|
Nishtha Pandey answered |
Part filled by A 1 min=1/32
part filled by B in 1 min=1/36
part emptied by C in 1 min=1/20
Net part filled in 1 min=1/32+1/36-1/20
=13/1440
the tank will be full in=1440/13 min
1/3rd of the tank will be full in=1440×3/13
=480/13
=36 12/13min
part filled by B in 1 min=1/36
part emptied by C in 1 min=1/20
Net part filled in 1 min=1/32+1/36-1/20
=13/1440
the tank will be full in=1440/13 min
1/3rd of the tank will be full in=1440×3/13
=480/13
=36 12/13min
Chapter doubts & questions for Time And Work - 4 Months Preparation Course for CLAT UG 2025 is part of CLAT exam preparation. The chapters have been prepared according to the CLAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CLAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Time And Work - 4 Months Preparation Course for CLAT UG in English & Hindi are available as part of CLAT exam.
Download more important topics, notes, lectures and mock test series for CLAT Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily