All Exams >
Class 10 >
6 Months Boards Preparation for Class 10 (CBSE) >
All Questions
All questions of Real Numbers for Class 10 Exam
The ratio between the LCM and HCF of 5,15, 20 is:- a)9 : 1
- b)4 : 3
- c)11 : 1
- d)12 : 1
Correct answer is option 'D'. Can you explain this answer?
The ratio between the LCM and HCF of 5,15, 20 is:
a)
9 : 1
b)
4 : 3
c)
11 : 1
d)
12 : 1
|
Ananya Das answered |
Factors are following:
5 = 5 x 1
15 = 5 x 3
20 = 2 x 2 x 5
5 = 5 x 1
15 = 5 x 3
20 = 2 x 2 x 5
LCM = 5 x 3 x 2 x 2 = 60
HCF = 5
Ratio = LCM/HCF = 60/5 = 12/1 = 12:1
HCF = 5
Ratio = LCM/HCF = 60/5 = 12/1 = 12:1
√7 is- a)an integer
- b)an irrational number
- c)a rational number
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
√7 is
a)
an integer
b)
an irrational number
c)
a rational number
d)
none of these
|
Baishali Kulkarni answered |
Lets assume that √7 is rational number. ie √7=p/q.
suppose p/q have common factor then
we divide by the common factor to get √7 = a/b were a and b are co-prime number.
that is a and b have no common factor.
√7 =a/b co- prime number
√7= a/b
a=√7b
squaring
a^2=7b^2 ....1
a� is divisible by 7
a=7c
substituting values in 1
(7c)^2=7b^2
49c^2=7b^2
7c^2=b^2
b^2=7c^2
b^2 is divisible by 7
that is a and b have atleast one common factor 7. This is contridite to the fact that a and b have no common factor.This is happen because of our wrong assumption.
√7 is irrational.
Find the greatest number of 5 digits, that will give us remainder of 5, when divided by 8 and 9 respectively.- a)99921
- b)99931
- c)99941
- d)99951
Correct answer is option 'C'. Can you explain this answer?
Find the greatest number of 5 digits, that will give us remainder of 5, when divided by 8 and 9 respectively.
a)
99921
b)
99931
c)
99941
d)
99951
|
|
Avinash Patel answered |
Greatest 5-Digit number = 99999
LCM of 8 and 9,
8 = 2 × 2 × 2
9 = 3 × 3
LCM = 2 × 2 × 2 × 3 × 3 = 72
Now, dividing 99999 by 72, we get
Quotient = 1388
Remainder = 63
So, the greatest 5-digit number divisible by 8 and 9 = 99999 - 63 = 99936
Required number = 99936 + 5 = 99941
If two positive integers p and q can be expressed as p = ab2 and q = a3b; where a, b being prime numbers, then LCM (p, q) is equal to- a)ab
- b)a2b2
- c)a3b2
- d)a2b3
Correct answer is option 'C'. Can you explain this answer?
If two positive integers p and q can be expressed as p = ab2 and q = a3b; where a, b being prime numbers, then LCM (p, q) is equal to
a)
ab
b)
a2b2
c)
a3b2
d)
a2b3
|
Meera Rana answered |
As per question, we have,
p = ab2 = a × b × b
q = a3b = a × a × a × b
So, their Least Common Multiple (LCM) = a3 × b2
p = ab2 = a × b × b
q = a3b = a × a × a × b
So, their Least Common Multiple (LCM) = a3 × b2
Which of the following rational numbers have a terminating decimal expansion?- a)125/441
- b)77/210
- c)15/1600
- d)
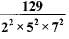
Correct answer is option 'C'. Can you explain this answer?
Which of the following rational numbers have a terminating decimal expansion?
a)
125/441
b)
77/210
c)
15/1600
d)
|
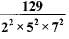
Dr Manju Sen answered |
The denominator 26 x 52 is of the form 2m x 5n, where m and n are non-negative integers. Hence, it is a terminating decimal expansion.
If two positive integers a and b are written as a = x3y2 and b = xy3 ; x, y are prime numbers, then HCF (a, b) is
- a)x4y3
- b)xy
- c)x2y3
- d) xy2
Correct answer is option 'D'. Can you explain this answer?
If two positive integers a and b are written as a = x3y2 and b = xy3 ; x, y are prime numbers, then HCF (a, b) is
a)
x4y3
b)
xy
c)
x2y3
d)
xy2
|
Diana Nair answered |
Correct option D because HCF is the highest common factor.So here in a and in b common factor are x and y and their HCF is x2y2.
Can you explain the answer of this question below:Find the largest number which divides 62,132,237 to leave the same reminder- A:30
- B:32
- C:35
- D:45
The answer is c.
Find the largest number which divides 62,132,237 to leave the same reminder
A:
30
B:
32
C:
35
D:
45
|
|
Anjana Khatri answered |
Trick is HCF of (237-132), (132-62), (237-62)
= HCF of (70,105,175) = 35
The relationship between HCF and LCM of two natural numbers is- a)HCF × LCM = Product of two natural numbers
- b)HCF × LCM = Sum of two natural numbers
- c)HCF × LCM = Difference of two natural numbers
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The relationship between HCF and LCM of two natural numbers is
a)
HCF × LCM = Product of two natural numbers
b)
HCF × LCM = Sum of two natural numbers
c)
HCF × LCM = Difference of two natural numbers
d)
None of these
|
|
Ananya Das answered |
The product of LCM and HCF of any two given natural numbers is equivalent to the product of the given numbers.
LCM × HCF = Product of the Numbers
Suppose A and B are two numbers, then.
LCM (A & B) × HCF (A & B) = A × B
Example: Prove that: LCM (9 & 12) × HCF (9 & 12) = Product of 9 and 12.
->LCM and HCF of 9 and 12:
9 = 3 × 3 = 3²
12 = 2 × 2 × 3 = 2² × 3
LCM of 9 and 12 = 2² × 3² = 4 × 9 = 36
HCF of 9 and 12 = 3
LCM (9 & 12) × HCF (9 & 12) = 36 × 3 = 108
Product of 9 and 12 = 9 × 12 = 108
Hence, LCM (9 & 12) × HCF (9 & 12) = 108 = 9 × 12
->LCM and HCF of 9 and 12:
9 = 3 × 3 = 3²
12 = 2 × 2 × 3 = 2² × 3
LCM of 9 and 12 = 2² × 3² = 4 × 9 = 36
HCF of 9 and 12 = 3
LCM (9 & 12) × HCF (9 & 12) = 36 × 3 = 108
Product of 9 and 12 = 9 × 12 = 108
Hence, LCM (9 & 12) × HCF (9 & 12) = 108 = 9 × 12
Every positive odd integer is of the form 2q + 1, where ‘q’ is some- a)whole number
- b)natural number
- c)integer
- d)none of these
Correct answer is 'C'. Can you explain this answer?
Every positive odd integer is of the form 2q + 1, where ‘q’ is some
a)
whole number
b)
natural number
c)
integer
d)
none of these
|
Rohan Kapoor answered |
Let a be any positive integer and b = 2.
Applying Euclid’s algorithm, we have:
a = 2q + r, for some integer q ≥ 0, and 0 ≤ r < 2
a = 2q or 2q + 1
If a = 2q, then a is an even integer.
Now, a positive integer can either be even or odd. Thus, any positive odd integer is of the form 2q + 1.
The multiplicative inverse of zero is- a)is 1
- b)is 0
- c)is 1/0
- d)does not exist
Correct answer is option 'B'. Can you explain this answer?
The multiplicative inverse of zero is
a)
is 1
b)
is 0
c)
is 1/0
d)
does not exist
|
Krishna Iyer answered |
Some rules associated with Multiplicative Inverse are discussed in following ways :-
Rule 1 = If product of two Fractional Numbers is equal to 1, then each of the Fractional Numbers is the Multiplicative Inverse of other.
Rule 2 = If the product of a Fractional Number and a Whole Number is equal to 1, then each is the Multiplicative Inverse of other.
Rule 3 = Multiplicative Inverse of 1 is also 1.
Rule 4 = Multiplicative Inverse of 0 (zero) does not exists
Rule 1 = If product of two Fractional Numbers is equal to 1, then each of the Fractional Numbers is the Multiplicative Inverse of other.
Rule 2 = If the product of a Fractional Number and a Whole Number is equal to 1, then each is the Multiplicative Inverse of other.
Rule 3 = Multiplicative Inverse of 1 is also 1.
Rule 4 = Multiplicative Inverse of 0 (zero) does not exists
If HCF(a, b) = 12 and a × b = 1800, then LCM(a, b) is- a)150
- b)90
- c)900
- d)1800
Correct answer is option 'A'. Can you explain this answer?
If HCF(a, b) = 12 and a × b = 1800, then LCM(a, b) is
a)
150
b)
90
c)
900
d)
1800
|
Anisha Mukherjee answered |
Using the result, HCF × LCM = Product of two natural numbers ⇒ LCM (a, b) = 1800/12 = 150
Which of the following is a rational number?- a)√15
- b)√9
- c)√10
- d)√12
Correct answer is option 'B'. Can you explain this answer?
Which of the following is a rational number?
a)
√15
b)
√9
c)
√10
d)
√12
|
Niharika Mehta answered |
√9 is a rational number because √9 = 3 and 3 is a rational number.
All non-terminating and non-recurring decimal numbers are- a)irrational numbers
- b)natural numbers
- c)rational numbers
- d)integers
Correct answer is option 'A'. Can you explain this answer?
All non-terminating and non-recurring decimal numbers are
a)
irrational numbers
b)
natural numbers
c)
rational numbers
d)
integers
|
|
Krishna Iyer answered |
All non-terminating and non-recurring decimal numbers are irrational numbers.
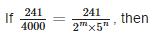
- a)m = 2 and n = 5
- b)m = 4 and n = 5
- c)m = 5 and n = 3
- d)m = 3 and n = 2
Correct answer is option 'C'. Can you explain this answer?
a)
m = 2 and n = 5
b)
m = 4 and n = 5
c)
m = 5 and n = 3
d)
m = 3 and n = 2
|
|
Anisha Mukherjee answered |
Comparing the denominators of both fractions, we have m = 5 and n = 3
If ‘p’ is a prime number, then √p is- a)Irrational
- b)Rational
- c)Integer
- d)prime number
Correct answer is 'A'. Can you explain this answer?
If ‘p’ is a prime number, then √p is
a)
Irrational
b)
Rational
c)
Integer
d)
prime number
|
|
Namita rane answered |
√p is an irrational number because square root of every prime number is an irrational number.
Can you explain the answer of this question below:The product of two numbers is -20/9. If one of the numbers is 4, find the other. - A:–5/9
- B:3/11
- C:12/39
- D:–9/11
The answer is a.
The product of two numbers is -20/9. If one of the numbers is 4, find the other.
A:
–5/9
B:
3/11
C:
12/39
D:
–9/11
|
|
Ananya Das answered |
We have two numbers such that their product is equal to -20/9.
So we have x*y=-20/9
One no. is given 4, so
x*4=-20/9
x=-20/9 = 4
x=-20/9 x 1/4=-5/9
So we have x*y=-20/9
One no. is given 4, so
x*4=-20/9
x=-20/9 = 4
x=-20/9 x 1/4=-5/9
The HCF of two consecutive numbers is- a)2
- b)3
- c)0
- d)1
Correct answer is 'D'. Can you explain this answer?
The HCF of two consecutive numbers is
a)
2
b)
3
c)
0
d)
1
|
Anshu Shah answered |
The HCF of two consecutive numbers is always 1.
The HCF of two consecutive even numbers is- a)1
- b)2
- c)0
- d)3
Correct answer is 'B'. Can you explain this answer?
The HCF of two consecutive even numbers is
a)
1
b)
2
c)
0
d)
3
|
|
Rajiv Gupta answered |
Let's take two consecutive even numbers i.e, 2x and 2x+2.
Method 1 : Factorisation
Now factor both numbers
2 * x and 2 * (x+1). Therefore, the only common factor we get here is one and only 2, which turns out to be HCF itself.
Hence, HCF of two even consecutive number is 2.
Example take 10 and 12 or 4 and 6 HCF always turns out to be 2 as
10=2*5 and 12=2*6
Method 2:
If we calculate through simple division process. Let's say two consecutive even numbers are n and n+2.
If n+2 is divided by n, we get the remainder as 2.
And n is divisible by 2 as it is an even number.
Hence, HCF is 2.
Any ____________ is of the form 4q + 1 or 4q + 3 for some integer ‘q’.- a)composite number
- b)positive odd integer
- c)prime number
- d)positive even integer
Correct answer is option 'B'. Can you explain this answer?
Any ____________ is of the form 4q + 1 or 4q + 3 for some integer ‘q’.
a)
composite number
b)
positive odd integer
c)
prime number
d)
positive even integer
|
Rohini Seth answered |
Let a be a given positive odd integer.
Applying Euclid’s Division Lemma to aa and b = 4,,
We have, a = 4q+r where 0 ⩽ r < 4 ⇒ r = 0, 1, 2, 3 ⇒ a = 4q or 4q+1 or 4q+2 or 4q+3
But a = 4q and 4q+2 = 2(2q+1)are clearly even.
Also a = 4q, 4q+1, 4q+2, 4q+3 are consecutive integers, therefore any positive odd integer is of the form 4q+1 and 4q+3 where q is some integer.
Applying Euclid’s Division Lemma to aa and b = 4,,
We have, a = 4q+r where 0 ⩽ r < 4 ⇒ r = 0, 1, 2, 3 ⇒ a = 4q or 4q+1 or 4q+2 or 4q+3
But a = 4q and 4q+2 = 2(2q+1)are clearly even.
Also a = 4q, 4q+1, 4q+2, 4q+3 are consecutive integers, therefore any positive odd integer is of the form 4q+1 and 4q+3 where q is some integer.
The least perfect square number which is divisible by 3, 4, 5, 6 and 8 is- a)900
- b)1200
- c)2500
- d)3600
Correct answer is option 'D'. Can you explain this answer?
The least perfect square number which is divisible by 3, 4, 5, 6 and 8 is
a)
900
b)
1200
c)
2500
d)
3600
|
Naina Sharma answered |
L.C.M. of 3, 4, 5, 6, 8 = 2 × 2 × 2 × 3 × 5 = 120
Pair of 2, 3 and 5 is not completed.
To make it a perfect square, the number should be multiplied by 2, 3, 5.
Pair of 2, 3 and 5 is not completed.
To make it a perfect square, the number should be multiplied by 2, 3, 5.
Required number = 120 x 2 x 3 x 5 = 3600.
If two positive integers a and b are written as a and x3y2 and b = xy3, where x, y are prime numbers, then HCF(a, b) is- a)xy
- b)xy2
- c)x3y3
- d)x2y2
Correct answer is option 'C'. Can you explain this answer?
If two positive integers a and b are written as a and x3y2 and b = xy3, where x, y are prime numbers, then HCF(a, b) is
a)
xy
b)
xy2
c)
x3y3
d)
x2y2
|
Gaurav Kumar answered |
Here, a = x3y2 and b = xy3.
⇒ a = x * x * x * y * y and b = xy * y * y
∴ LCM(a, b) = x * x * x * y * y * y = x3 * y3 = x3y3
LCM = x3y3
⇒ a = x * x * x * y * y and b = xy * y * y
∴ LCM(a, b) = x * x * x * y * y * y = x3 * y3 = x3y3
LCM = x3y3
If 112 = q×6+r, then the possible values of r are:
- A:2, 3, 5
- B:0, 1, 2, 3, 4, 5
- C:1, 2, 3, 4
- D:0, 1, 2, 3
The answer is b.
A:
2, 3, 5
B:
0, 1, 2, 3, 4, 5
C:
1, 2, 3, 4
D:
0, 1, 2, 3
|
|
Ananya Das answered |
For the relation x = qy+r, 0 ⩽ r < y So, here r lies between 0 ⩽ r < 6. Hence r = 0, 1, 2, 3, 4, 5
The HCF of two consecutive numbers is- a)2
- b)3
- c)0
- d)1
Correct answer is option 'D'. Can you explain this answer?
The HCF of two consecutive numbers is
a)
2
b)
3
c)
0
d)
1
|
Akshara Basu answered |
The HCF of two consecutive numbers is always 1.
If ‘a’ and ‘b’ are both positive rational numbers, then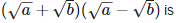 
- a)neither rational nor rational number
- b)an irrational number
- c)a rational number
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If ‘a’ and ‘b’ are both positive rational numbers, then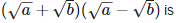
a)
neither rational nor rational number
b)
an irrational number
c)
a rational number
d)
none of these
|
|
Avinash Patel answered |
= (a−b) Since a and b both are positive rational numbers, therefore difference of two positive rational numbers is also rational.
If two positive integers a and b are written as a = x3y2 and b = xy3; x, y are prime numbers, then LCM (a, b) is- a)xy
- b)xy2
- c)x3y3
- d)x2y2
Correct answer is option 'C'. Can you explain this answer?
If two positive integers a and b are written as a = x3y2 and b = xy3; x, y are prime numbers, then LCM (a, b) is
a)
xy
b)
xy2
c)
x3y3
d)
x2y2
|
|
Wahid Khan answered |
A=x3y2=x(x)(x)(y)(y)
b=xy3=x(y)(y)(y)
LCM of a and b=xy2(x2×y)
=x3y3
so option C is the correct answer
b=xy3=x(y)(y)(y)
LCM of a and b=xy2(x2×y)
=x3y3
so option C is the correct answer
Which of the following numbers has terminating decimal expansion?- a)3/11
- b)3/5
- c)5/3
- d)3/7
Correct answer is option 'B'. Can you explain this answer?
Which of the following numbers has terminating decimal expansion?
a)
3/11
b)
3/5
c)
5/3
d)
3/7
|
Clifford Academy answered |
52n −22n is of the form a2n − b2n which is divisible by both (a + b) and (a – b).
So, 52n − 22n is divisible by both 7, 3.
So, 52n − 22n is divisible by both 7, 3.
There are 576 boys and 448 girls in a school that are to be divided into equal sections of either boys or girls alone. The total number of sections thus formed are:
- a)22
- b)16
- c)36
- d)21
Correct answer is option 'B'. Can you explain this answer?
There are 576 boys and 448 girls in a school that are to be divided into equal sections of either boys or girls alone. The total number of sections thus formed are:
a)
22
b)
16
c)
36
d)
21
|
|
Gaurav Kumar answered |
The number 576 can be factorised as,
576 = 2×2×2×2×2×2×3×3
The number 448 can be factorised as,
448=2×2×2×2×2×2×7
Write the common factors of the given numbers.
2×2×2×2×2×22×2×2×2×2×2
Multiply the common factors to determine the highest common factor (HCF) of the given numbers.
2×2×2×2×2×2 = 642×2×2×2×2×2 = 64
Since the highest common factor (HCF) of the given numbers is 64, this implies that each section will have 64 number of students.
Now, we need to find the number of sections formed.
Let us first find the number of sections formed by the total number of boys by dividing 576 by 64.
576/64 = 9
Now, find the number of sections formed by the total number of girls by dividing 448 by 64.
448/64=7
Thus, the total number of sections formed will be 9+7=16
Hence, option B is the correct answer.
576 = 2×2×2×2×2×2×3×3
The number 448 can be factorised as,
448=2×2×2×2×2×2×7
Write the common factors of the given numbers.
2×2×2×2×2×22×2×2×2×2×2
Multiply the common factors to determine the highest common factor (HCF) of the given numbers.
2×2×2×2×2×2 = 642×2×2×2×2×2 = 64
Since the highest common factor (HCF) of the given numbers is 64, this implies that each section will have 64 number of students.
Now, we need to find the number of sections formed.
Let us first find the number of sections formed by the total number of boys by dividing 576 by 64.
576/64 = 9
Now, find the number of sections formed by the total number of girls by dividing 448 by 64.
448/64=7
Thus, the total number of sections formed will be 9+7=16
Hence, option B is the correct answer.
A rational number can be expressed as a terminating decimal if the denominator has the factors- a)2 or 5 only
- b)2 or 3 only
- c)2 and 5 only
- d)2, 3 or 5 only
Correct answer is option 'A'. Can you explain this answer?
A rational number can be expressed as a terminating decimal if the denominator has the factors
a)
2 or 5 only
b)
2 or 3 only
c)
2 and 5 only
d)
2, 3 or 5 only
|
Vikas Kumar answered |
If the denominator of rational number contains no prime factors other then 2 or 5 or both, then this rational number can be expressed as terminating decimal.
A rational number can be expressed as a non-terminating repeating decimal if the denominator has the factors- a)other than 2 or 5
- b)2 or 3 only
- c)2 or 5 only
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
A rational number can be expressed as a non-terminating repeating decimal if the denominator has the factors
a)
other than 2 or 5
b)
2 or 3 only
c)
2 or 5 only
d)
none of these
|
Pooja Shah answered |
A rational number can be expressed as a non-terminating repeating decimal if the denominator has the factors other than 2 or 5.
The LCM of two number is 45 times their HCF. If one of the numbers is 125 and the sum of HCF and LCM is 1150, the other number is:- a)215
- b)220
- c)225
- d)235
Correct answer is option 'C'. Can you explain this answer?
The LCM of two number is 45 times their HCF. If one of the numbers is 125 and the sum of HCF and LCM is 1150, the other number is:
a)
215
b)
220
c)
225
d)
235
|
|
Rahul Kapoor answered |
Let the lcm be x and hcf be y and the other number be z.
Given lcm of 2 numbers is 45 times their hcf, the sum of HCF + LCM is 1150.
y = 45x. ---- (1)
x + y = 1150 --- (2)
Substitute equation (1) in (2), we get
46x = 1150
x = 25.
Substitute x = 25 in (1), we get
y = 45 * 25 = 1125.
We know that product of two numbers = LCM * HCF
125 * z = 25 * 1125
z = 25 * 1125/125
= 225.
The other number = 225.
The product of a non zero rational and an irrational number is
- a)Always irrational
- b)Always rational
- c)Rational or irrational
- d)One
Correct answer is option 'A'. Can you explain this answer?
The product of a non zero rational and an irrational number is
a)
Always irrational
b)
Always rational
c)
Rational or irrational
d)
One
|
|
Rising Star answered |
The product will always be irrational...
let us have an example--}
2( rational number) *√2(irrational number)=2√2(irrational)..
let us have an example--}
2( rational number) *√2(irrational number)=2√2(irrational)..
If 112 = q×6+r, then the possible values of r are:- a)2, 3, 5
- b)0, 1, 2, 3, 4, 5
- c)1, 2, 3, 4
- d)0, 1, 2, 3
Correct answer is option 'B'. Can you explain this answer?
If 112 = q×6+r, then the possible values of r are:
a)
2, 3, 5
b)
0, 1, 2, 3, 4, 5
c)
1, 2, 3, 4
d)
0, 1, 2, 3
|
Athira Yadav answered |
For the relation x = qy+r, 0 ⩽ r < y So, here r lies between 0 ⩽ r < 6. Hence r = 0, 1, 2, 3, 4, 5
Two alarm clocks ring their alarms at regular intervals of 50 seconds and 48 seconds. If they first beep together at 12 noon, at what time will they beep again for the first time?- a)12.20 pm
- b)12.12 pm
- c)12.11 pm
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
Two alarm clocks ring their alarms at regular intervals of 50 seconds and 48 seconds. If they first beep together at 12 noon, at what time will they beep again for the first time?
a)
12.20 pm
b)
12.12 pm
c)
12.11 pm
d)
none of these
|
|
Ananya Das answered |
LCM of 50 and 48 = 1200
∴ 1200 sec = 20 min
Hence at 12.20 pm they will beep again for the first time.
∴ 1200 sec = 20 min
Hence at 12.20 pm they will beep again for the first time.
Which of the following is false:- a)H.C.F.(p,q,r) × L.C.M.(p,q,r) = p×q×r
- b)H.C.F.(p,q,r) = 1; if p,q,r are prime numbers
- c)H.C.F.(a,b) × L.C.M.(a,b) = a×b
- d)L.C.M.(p,q,r) = p×q×r; if p,q,r are prime numbers
Correct answer is option 'A'. Can you explain this answer?
Which of the following is false:
a)
H.C.F.(p,q,r) × L.C.M.(p,q,r) = p×q×r
b)
H.C.F.(p,q,r) = 1; if p,q,r are prime numbers
c)
H.C.F.(a,b) × L.C.M.(a,b) = a×b
d)
L.C.M.(p,q,r) = p×q×r; if p,q,r are prime numbers
|
|
Raghav Bansal answered |
H.C.F.(p,q,r)× L.C.M.(p,q,r) ≠ p×q×r. This condition is only applied on HCF and LCM of two numbers.
If aa is a non-zero rational and √b is irrational, then a√b is:- a)a rational number
- b)an irrational number
- c)an integer
- d)a natural number
Correct answer is option 'B'. Can you explain this answer?
If aa is a non-zero rational and √b is irrational, then a√b is:
a)
a rational number
b)
an irrational number
c)
an integer
d)
a natural number
|
|
Krishna Iyer answered |
If possible let a√b be rational. Then a√b = p/q,
where p and q are non-zero integers, having no common factor other than 1.
Now, a√b = p/q ⇒ √b = p/aq……….(i)
But, p and aq are both rational and aq ≠ 0.
∵ p/aq is rational.
Therefore, from eq. (i), it follows that √b is rational.
The contradiction arises by assuming that a√b is rational.
Hence, a√b is irrational.
where p and q are non-zero integers, having no common factor other than 1.
Now, a√b = p/q ⇒ √b = p/aq……….(i)
But, p and aq are both rational and aq ≠ 0.
∵ p/aq is rational.
Therefore, from eq. (i), it follows that √b is rational.
The contradiction arises by assuming that a√b is rational.
Hence, a√b is irrational.
The least positive integer divisible by 20 and 24 is- a)360
- b)120
- c)480
- d)240
Correct answer is option 'B'. Can you explain this answer?
The least positive integer divisible by 20 and 24 is
a)
360
b)
120
c)
480
d)
240
|
|
Aditya Shah answered |
Here is your answer :
Given numbers are 20 and 24
Prime factorization of 20 = 2 x 2 x 5
Prime factorization of 24 = 2 x 2 x 2 x 3
LCM of 20 and 24 = 2 x 2 x 2 x 3 x 5
Hence, 120 is the least divisible by 20 and 24.
Prime factorization of 20 = 2 x 2 x 5
Prime factorization of 24 = 2 x 2 x 2 x 3
LCM of 20 and 24 = 2 x 2 x 2 x 3 x 5
Hence, 120 is the least divisible by 20 and 24.
You can study about basics of Real Numbers through the document:
The decimal expansion of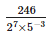 
terminates after:- a)7 places of decimals
- b)10 places of decimals
- c)can’t be determined
- d)6 places of decimals
Correct answer is option 'D'. Can you explain this answer?
The decimal expansion of 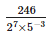terminates after:
terminates after:a)
7 places of decimals
b)
10 places of decimals
c)
can’t be determined
d)
6 places of decimals
|
Shivani Shah answered |
Therefore, 
will terminate after 6 places of decimals.The number 
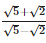is- a)an irrational number
- b)an integer
- c)a rational number
- d)not a real number
Correct answer is option 'A'. Can you explain this answer?
The number 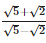is
isa)
an irrational number
b)
an integer
c)
a rational number
d)
not a real number
|
|
Krishna Iyer answered |
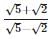
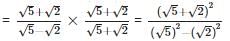
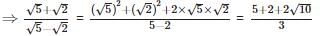
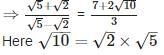
Since √2 and √5 both are irrational number therefore
is an irrational number.The number (√3+√5)2 is- a)a rational number
- b)an irrational number
- c)an integer
- d)not a real number
Correct answer is option 'B'. Can you explain this answer?
The number (√3+√5)2 is
a)
a rational number
b)
an irrational number
c)
an integer
d)
not a real number
|
Om Khanna answered |
Since √3 and √5 both are irrational number therefore (√3+√5)2 is an irrational number.
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of ‘m’ is- a)4
- b)1
- c)3
- d)2
Correct answer is 'D'. Can you explain this answer?
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of ‘m’ is
a)
4
b)
1
c)
3
d)
2
|
|
Pragya joshi answered |
First of all find the HCF of 65 and 117,
117 = 1×65 + 52
65 = 1× 52 + 13
52 = 4 ×13 + 0
∴ HCF of 65 and 117 is 13.
65m - 117 = 13
65m = 117+13 = 130
∴m =130/65 = 2
The LCM of 24, 60 and 150 is- a)1800
- b)1200
- c)600
- d)2400
Correct answer is option 'C'. Can you explain this answer?
The LCM of 24, 60 and 150 is
a)
1800
b)
1200
c)
600
d)
2400
|
|
Chetan nair answered |
Finding the LCM of 24, 60 and 150
To find the LCM of 24, 60, and 150, we need to follow these steps:
Step 1: Prime factorization
We need to find the prime factors of each number:
- 24 = 2 x 2 x 2 x 3
- 60 = 2 x 2 x 3 x 5
- 150 = 2 x 3 x 5 x 5
Step 2: Identify common factors
We need to identify the common factors among the prime factorizations of the numbers. We can see that 2 and 3 are the common factors.
Step 3: Multiply common factors
We need to multiply the common factors once and any remaining factors from each number:
- 2 x 2 x 2 x 3 x 5 x 5 = 600
Therefore, the LCM of 24, 60, and 150 is 600. Answer: (c) 600.
To find the LCM of 24, 60, and 150, we need to follow these steps:
Step 1: Prime factorization
We need to find the prime factors of each number:
- 24 = 2 x 2 x 2 x 3
- 60 = 2 x 2 x 3 x 5
- 150 = 2 x 3 x 5 x 5
Step 2: Identify common factors
We need to identify the common factors among the prime factorizations of the numbers. We can see that 2 and 3 are the common factors.
Step 3: Multiply common factors
We need to multiply the common factors once and any remaining factors from each number:
- 2 x 2 x 2 x 3 x 5 x 5 = 600
Therefore, the LCM of 24, 60, and 150 is 600. Answer: (c) 600.
Pairs of natural numbers whose least common multiple is 78 and the greatest common divisor is 13 are: - a)58 and 13 or 16 and 29
- b)68 and 23 or 36 and 49
- c)18 and 73 or 56 and 93
- d)78 and 13 or 26 and 39
Correct answer is option 'D'. Can you explain this answer?
Pairs of natural numbers whose least common multiple is 78 and the greatest common divisor is 13 are:
a)
58 and 13 or 16 and 29
b)
68 and 23 or 36 and 49
c)
18 and 73 or 56 and 93
d)
78 and 13 or 26 and 39
|
|
Om Khanna answered |
Given- least common factor (LCM) = 78
Greatest divisor is also a HCF = 13
As, we know , HCF x LCM = A x B ( A and B are two natural no. of which LCM and HCF is given)
Therefore, req product of no. = 13 x 78 = A x B =1014 or 2*3*13*13
since 13 is common in both no. as its hcf is 13
req no.= 13*3=39 and 13*2 = 26
The product of two numbers is -20/9. If one of the numbers is 4, find the other. - a)–5/9
- b)3/11
- c)12/39
- d)–9/11
Correct answer is 'A'. Can you explain this answer?
The product of two numbers is -20/9. If one of the numbers is 4, find the other.
a)
–5/9
b)
3/11
c)
12/39
d)
–9/11
|
|
Amit Sharma answered |
We have two numbers such that their product is equal to -20/9.
So we have x*y=-20/9
One no. is given 4, so
x*4=-20/9
x=-20/9 = 4
x=-20/9 x 1/4=-5/9
So we have x*y=-20/9
One no. is given 4, so
x*4=-20/9
x=-20/9 = 4
x=-20/9 x 1/4=-5/9
The largest number of 4 digits exactly divisible by 12, 15, 18 and 27 is- a)9720
- b)1000
- c)9270
- d)9999
Correct answer is 'A'. Can you explain this answer?
The largest number of 4 digits exactly divisible by 12, 15, 18 and 27 is
a)
9720
b)
1000
c)
9270
d)
9999
|
Maitri Kulkarni answered |
LCM (12, 15, 18, 27) = 540
Now, largest four digit number = 9999
∴ 9999 ÷ 540 = 18 x 540 + 279 (Remainder = 279) Therefore, the largest number of 4 digits exactly divisible by 12, 15, 18 and 27 is 9999 – 279 = 9720
Now, largest four digit number = 9999
∴ 9999 ÷ 540 = 18 x 540 + 279 (Remainder = 279) Therefore, the largest number of 4 digits exactly divisible by 12, 15, 18 and 27 is 9999 – 279 = 9720
The sum of a rational number and an irrational number is always:- a)Rational
- b)Irrational
- c)Whole number
- d)Integer
Correct answer is option 'B'. Can you explain this answer?
The sum of a rational number and an irrational number is always:
a)
Rational
b)
Irrational
c)
Whole number
d)
Integer
|
|
Mohd Talha Raza answered |
Hey, I am using the EduRev app for learning videos, tests & discussions. I am sure you would love it too! It will be fun together, just try it out: https://play.google.com/store/apps/details?id=com.edurev&referrer=ZAR5982
Chapter doubts & questions for Real Numbers - 6 Months Boards Preparation for Class 10 (CBSE) 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Real Numbers - 6 Months Boards Preparation for Class 10 (CBSE) in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
6 Months Boards Preparation for Class 10 (CBSE)
344 videos|2427 docs|372 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup