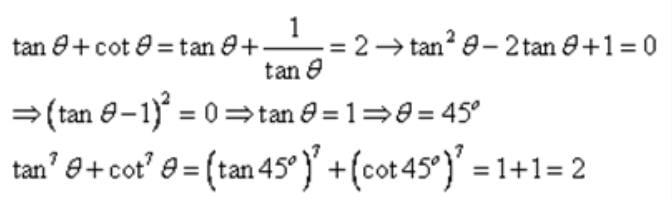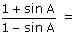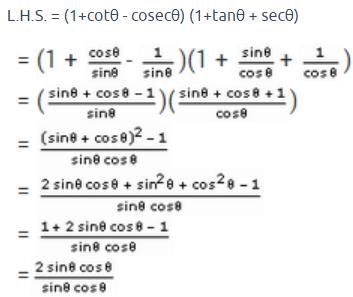All Exams >
Class 10 >
6 Months Boards Preparation for Class 10 (CBSE) >
All Questions
All questions of Introduction to Trigonometry for Class 10 Exam
If tan A = 3/2, then the value of cos A is- a)
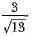
- b)
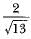
- c)2/3
- d)
Correct answer is option 'B'. Can you explain this answer?
If tan A = 3/2, then the value of cos A is
a)
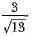
b)
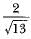
c)
2/3
d)
|
EduRev Class 10 answered |
Tanθ = Perpendicular / Base
We are given that TanA = 3/2
On comparing
Perpendicular = 3
Base = 2
To fing hypotenuse
Hypotenuse2 = Perpendicular2 + Base2
Hypotenuse2 = 32 + 22
Hypotenuse =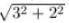
Hypotenuse = 3.6
We are given that TanA = 3/2
On comparing
Perpendicular = 3
Base = 2
To fing hypotenuse
Hypotenuse2 = Perpendicular2 + Base2
Hypotenuse2 = 32 + 22
Hypotenuse =
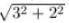
Hypotenuse = 3.6
Cosθ = Base / Hypotenuse
CosA = 2 / 3.6
Hence the value of Cos A is 2/3.6=2/√13
CosA = 2 / 3.6
Hence the value of Cos A is 2/3.6=2/√13
If tan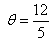 
, then 
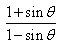is equal to- a)24
- b)12/13
- c)25
- d)9
Correct answer is option 'C'. Can you explain this answer?
If tan 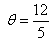, then 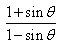is equal to
, then is equal toa)
24
b)
12/13
c)
25
d)
9
|
Vp Classes answered |
tanθ = 12/5
so sinθ = 12/13
so
(1 + 12/13)/(1-12/13)
= 25/1 = 25
The value of (sin 30° + cos 30°) - (sin 60° + cos 60°) is- a)-1
- b)0
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
The value of (sin 30° + cos 30°) - (sin 60° + cos 60°) is
a)
-1
b)
0
c)
1
d)
2
|
Ritu Saxena answered |
sin 30° = 1/2,
cos 30°=√3/2,
sin 60°=√3/2,
cos 60°=1/2,
By putting the value of sin 30°, cos 30°, sin 60° and cos 60° in equation
cos 30°=√3/2,
sin 60°=√3/2,
cos 60°=1/2,
By putting the value of sin 30°, cos 30°, sin 60° and cos 60° in equation
We get=
(sin30°+cos30°)-(sin60°+cos60°)=(1/2+√3/2)-(√3/2+1/2)
=0
(sin30°+cos30°)-(sin60°+cos60°)=(1/2+√3/2)-(√3/2+1/2)
=0
The value of (sin 45° + cos 45°) is- a)1/√2
- b)√2
- c)√3/2
- d)1
Correct answer is option 'B'. Can you explain this answer?
The value of (sin 45° + cos 45°) is
a)
1/√2
b)
√2
c)
√3/2
d)
1
|
Krishna Iyer answered |
sin 45° + cos 45°
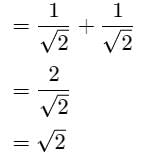
Hence, the answer is = √2
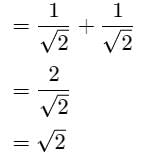
Hence, the answer is = √2
Can you explain the answer of this question below:If 7sin2x + 3cos2x = 4 then , secx + cosecx =- A:
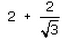
- B:
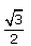
- C:
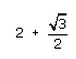
- D:
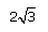
The answer is a.
If 7sin2x + 3cos2x = 4 then , secx + cosecx =
A:
B:
C:
D:
|
Gunjan Lakhani answered |
7sin2x+3cos2 x=4
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=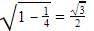
Sec x= 1/cos x=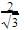
Cosec x + sec x=2+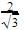
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=
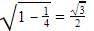
Sec x= 1/cos x=
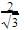
Cosec x + sec x=2+
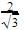
The value of the expression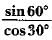 
is- a)√3/2
- b)1/2
- c)1
- d)2
Correct answer is option 'C'. Can you explain this answer?
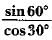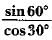The value of the expression is
isa)
√3/2
b)
1/2
c)
1
d)
2
|
|
Krishna Iyer answered |
We know that sin 60 =√3/2 and cos 30 = √3/2.
Therefore , Sin 60/cos 30= (√3/2)/(√3/2) = 1
Therefore , Sin 60/cos 30= (√3/2)/(√3/2) = 1
If tan θ = a/b then the value of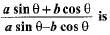 
- a)
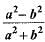
- b)
- c)
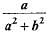
- d)
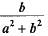
Correct answer is option 'B'. Can you explain this answer?
If tan θ = a/b then the value of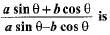
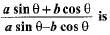
a)
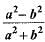
b)
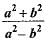
c)
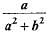
d)
|
|
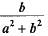
Vp Classes answered |
Let,angle= θ
(asinθ + bcosθ)/(asinθ - bcosθ)
Dividing both numerator and denominator from cosθ
We get,
atanθ +b/atanθ - b
= ( a.a/b + b) /(a.a/b - b) =(a²/b +b)/(a²/b - b)
=(a² + b²/a²- b²)
(asinθ + bcosθ)/(asinθ - bcosθ)
Dividing both numerator and denominator from cosθ
We get,
atanθ +b/atanθ - b
= ( a.a/b + b) /(a.a/b - b) =(a²/b +b)/(a²/b - b)
=(a² + b²/a²- b²)
If 6cotθ + 2cosecθ = cotθ + 5cosecθ, then cosθ is- a)4/5
- b)5/3
- c)3/5
- d)5/4
Correct answer is option 'C'. Can you explain this answer?
If 6cotθ + 2cosecθ = cotθ + 5cosecθ, then cosθ is
a)
4/5
b)
5/3
c)
3/5
d)
5/4
|
|
Raghav Bansal answered |
6cot+2cosec=cot+5cosec
6cot-cot=5cosec-2cosec
5cot=3cosec
5cos/sin=3/sin
cos=3/5
6cot-cot=5cosec-2cosec
5cot=3cosec
5cos/sin=3/sin
cos=3/5
If ΔABC is right angled at C, then the value of cos (A + B) is- a)0
- b)1
- c)1/2
- d)√3/2
Correct answer is option 'A'. Can you explain this answer?
If ΔABC is right angled at C, then the value of cos (A + B) is
a)
0
b)
1
c)
1/2
d)
√3/2
|
Aniket Chavan answered |
Since ABC is right-angled and angle C is 90degree
therefore,
A+B=180degree - C
A+B=180degree-90degree
A+B= 90degree
Therefore,cos (A+B)=cos90degree
=0
Match the Columns:
- a)1 - A, 2 - C, 3 - B
- b)1 - B, 2 - C, 3 - A
- c)1 - B, 2 - C, 3 - D
- d)1 - D , 2 - B , 3 - A
Correct answer is option 'B'. Can you explain this answer?
Match the Columns:
a)
1 - A, 2 - C, 3 - B
b)
1 - B, 2 - C, 3 - A
c)
1 - B, 2 - C, 3 - D
d)
1 - D , 2 - B , 3 - A
|
|
Krishna Iyer answered |
Correct Answer :- b
Explanation : If θ is one of the acute angles in a triangle, then the sine of theta is the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side.
9 sec2 A - 9tan2 A is equal to- a)1
- b)9
- c)8
- d)0
Correct answer is option 'B'. Can you explain this answer?
9 sec2 A - 9tan2 A is equal to
a)
1
b)
9
c)
8
d)
0
|
|
Kiran Mehta answered |
9 sec2 A - 9 tan2 A
= 9( sec2 A - tan2 A)
= 9 × 1
= 9
= 9( sec2 A - tan2 A)
= 9 × 1
= 9
If cosec A - cot A = 4/5, then cosec A = - a)47/40
- b)59/40
- c)51/40
- d)41/40
Correct answer is option 'D'. Can you explain this answer?
If cosec A - cot A = 4/5, then cosec A =
a)
47/40
b)
59/40
c)
51/40
d)
41/40
|
Abhiram Malik answered |
cosecA = 41/40
Explanation :
cosecA - cotA = 4/5 ---( 1 )
=> (cosecA - cotA)(cosecA + cotA)=(4/5) (cosecA + cotA)
=> (cosec�A-cot�A) = (4/5)(cosecA +cotA)
=> 1 = (4/5)(cosecA + cotA)
=> cosecA +cotA = 5/4 ---(2)
Now ,
Add (1) and (2 ), we get
=> 2coseecA = (4/5+5/4)
=> 2cosecA = (16+25)/20
=> cosecA = 41/40
Therefore,
cosecA = 41/40
Ratios of sides of a right triangle with respect to its acute angles are known as- a)trigonometric identities
- b)trigonometry
- c)trigonometric ratios of the angles
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Ratios of sides of a right triangle with respect to its acute angles are known as
a)
trigonometric identities
b)
trigonometry
c)
trigonometric ratios of the angles
d)
none of these
|
Ishan Choudhury answered |
The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle.
7 sin2 θ + 3 cos2 θ = 4 then :- a)tan θ = 1/√2
- b)tan θ = 1/2
- c)tan θ = 1/3
- d)tan θ = 1/√3
Correct answer is option 'D'. Can you explain this answer?
7 sin2 θ + 3 cos2 θ = 4 then :
a)
tan θ = 1/√2
b)
tan θ = 1/2
c)
tan θ = 1/3
d)
tan θ = 1/√3
|
|
Nirmal Kumar answered |
7Sin²A+3Cos²A=4,
3Cos²A+3Sin²A+4Sin²A=4,
3(sin²A+Cos²A)+4sin²A=4,
4Sin²A=1,
sin²A=1/2×1/2,
SinA=1/2=Sin 30,
A=30,
tanA=tan30=1/√3
3Cos²A+3Sin²A+4Sin²A=4,
3(sin²A+Cos²A)+4sin²A=4,
4Sin²A=1,
sin²A=1/2×1/2,
SinA=1/2=Sin 30,
A=30,
tanA=tan30=1/√3
The value of 3/4 tan2 30° – 3 sin2 60° + cosec2 45° is- a)1
- b)8
- c)0
- d)12
Correct answer is option 'C'. Can you explain this answer?
The value of 3/4 tan2 30° – 3 sin2 60° + cosec2 45° is
a)
1
b)
8
c)
0
d)
12
|
|
Malini shah answered |
To solve for the value of 3/4tan230, we need to use a calculator. Here are the steps:
1. Press the "tan" button on your calculator.
2. Type in "230".
3. Press the "equals" button.
4. Take note of the value shown on the screen.
5. Divide the value by 4.
6. Multiply the result by 3.
The final answer will depend on the degree of accuracy you need. Rounded to two decimal places, the value of 3/4tan230 is approximately -1.42.
In sin 3θ = cos (θ – 26°), where 3θ and (θ – 26°) are acute angles, then value of θ is :- a)30°
- b)29°
- c)27°
- d)26°
Correct answer is option 'B'. Can you explain this answer?
In sin 3θ = cos (θ – 26°), where 3θ and (θ – 26°) are acute angles, then value of θ is :
a)
30°
b)
29°
c)
27°
d)
26°
|
|
Krishna Iyer answered |
sin3θ = cos(θ - 26°)
=> cos(90° - 3θ) = cos(θ - 26°)
=> 90° - 3θ = θ - 26°
=> 3θ + θ = 90° + 26°
=> 4θ = 116°
=> θ = 116°/4
=> θ = 29°
=> cos(90° - 3θ) = cos(θ - 26°)
=> 90° - 3θ = θ - 26°
=> 3θ + θ = 90° + 26°
=> 4θ = 116°
=> θ = 116°/4
=> θ = 29°
The value of sin2 15° + sin2 30° + sin2 45° + sin2 60° + sin2 75° is :- a)1
- b)3/2
- c)5/2
- d)3
Correct answer is option 'C'. Can you explain this answer?
The value of sin2 15° + sin2 30° + sin2 45° + sin2 60° + sin2 75° is :
a)
1
b)
3/2
c)
5/2
d)
3
|
|
Avi Saini answered |
The value of sin(215) in degrees is approximately -0.574.
If angle A is acute and cos A = 8/17 then cot A is :- a)8/15
- b)17/8
- c)15/8
- d)17/15
Correct answer is option 'A'. Can you explain this answer?
If angle A is acute and cos A = 8/17 then cot A is :
a)
8/15
b)
17/8
c)
15/8
d)
17/15
|
Pooja Shah answered |
Cos A=8/17=B/H
base=8x, hypotenuse=17x
By pythagoras theorem,
H2 =P2 + B2
289x2 = P2 + 64x2
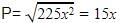
Cot A=B/P=8x/15x=8/15
base=8x, hypotenuse=17x
By pythagoras theorem,
H2 =P2 + B2
289x2 = P2 + 64x2
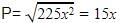
Cot A=B/P=8x/15x=8/15
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is:- a)√5 m
- b)√15 m
- c)6 m
- d)2.25 m.
Correct answer is option 'C'. Can you explain this answer?
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is:
a)
√5 m
b)
√15 m
c)
6 m
d)
2.25 m.
|
|
Pooja Shah answered |
Given AB is the tower.
P and Q are the points at distance of 4m and 9m respectively.
From fig, PB = 4m, QB = 9m.
Let angle of elevation from P be α and angle of elevation from Q be β.
Given that α and β are supplementary. Thus, α + β = 90
In triangle ABP,
tan α = AB/BP – (i)
In triangle ABQ,
tan β = AB/BQ
tan (90 – α) = AB/BQ (Since, α + β = 90)
cot α = AB/BQ
1/tan α = AB/BQ
So, tan α = BQ/AB – (ii)
From (i) and (ii)
AB/BP = BQ/AB
AB^2 = BQ x BP
AB^2 = 4 x 9
AB^2 = 36
Therefore, AB = 6.
Hence, height of tower is 6m.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angles of elevation from his eyes to the top of the building increases from 30 to 60° as he walks towards the building. The distance he walked towards the building is :- a)19 √3 m
- b)57(√3)3 m
- c)38 √3 m
- d)18 √3 m
Correct answer is option 'A'. Can you explain this answer?
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angles of elevation from his eyes to the top of the building increases from 30 to 60° as he walks towards the building. The distance he walked towards the building is :
a)
19 √3 m
b)
57(√3)3 m
c)
38 √3 m
d)
18 √3 m
|
|
Rising Star answered |
If 3 cot θ = 2, then the value of tan θ- a)2/3
- b)3/2
- c)
- d)
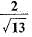
Correct answer is option 'B'. Can you explain this answer?
If 3 cot θ = 2, then the value of tan θ
a)
2/3
b)
3/2
c)
d)
|
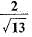
Hrishikesh Choudhary answered |
3cot theta =2
=> cot theta = 2/3
=> 1/tan theta =2/3
=>. tan theta = 3/2
hence, the answer is tan theta =3/2
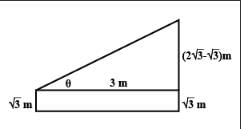
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks then the width of the river is :- a)3 (√3 –1)m
- b)3 (√3 +1)m
- c)(3 + √3)m
- d)(3 – √3 )m.
Correct answer is option 'B'. Can you explain this answer?
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks then the width of the river is :
a)
3 (√3 –1)m
b)
3 (√3 +1)m
c)
(3 + √3)m
d)
(3 – √3 )m.
|
|
Subham Ghosh answered |
° and 45°. If the bridge is 80 meters long, how wide is the river?
Let's label the diagram:
We want to find the width of the river, which is represented by the distance between points A and B.
To solve this problem, we need to use trigonometry. Specifically, we can use the tangent function:
tan(angle) = opposite/adjacent
We can use this formula for both angles of depression:
tan(30°) = AB/80
tan(45°) = AC/80
Simplifying these equations, we get:
AB = 80 tan(30°) ≈ 46.4 meters
AC = 80 tan(45°) ≈ 80 meters
Now we can use the Pythagorean theorem to find the length of BC:
BC^2 = AC^2 - AB^2
BC^2 = (80)^2 - (46.4)^2
BC ≈ 64.1 meters
Therefore, the width of the river (AB) is approximately 46.4 meters, and the length of the bridge (BC) is approximately 64.1 meters.
Let's label the diagram:
We want to find the width of the river, which is represented by the distance between points A and B.
To solve this problem, we need to use trigonometry. Specifically, we can use the tangent function:
tan(angle) = opposite/adjacent
We can use this formula for both angles of depression:
tan(30°) = AB/80
tan(45°) = AC/80
Simplifying these equations, we get:
AB = 80 tan(30°) ≈ 46.4 meters
AC = 80 tan(45°) ≈ 80 meters
Now we can use the Pythagorean theorem to find the length of BC:
BC^2 = AC^2 - AB^2
BC^2 = (80)^2 - (46.4)^2
BC ≈ 64.1 meters
Therefore, the width of the river (AB) is approximately 46.4 meters, and the length of the bridge (BC) is approximately 64.1 meters.
The solution of the trigonometric equation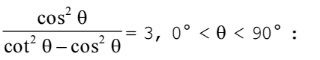 
- a)θ = 0°
- b)θ = 30°
- c)θ = 60°
- d)θ = 90°
Correct answer is option 'C'. Can you explain this answer?
The solution of the trigonometric equation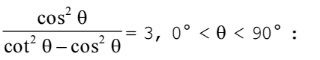
a)
θ = 0°
b)
θ = 30°
c)
θ = 60°
d)
θ = 90°
|
|
Krishna Iyer answered |
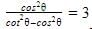
cos2θ = 3(cot2θ-cos2θ)
4cos2θ = 3cot2θ
4=3(1/sin2θ)
sin2θ = 3/4
sinθ = √3/2
θ = 60
The value of 2 tan2 60° – 4 cos2 45° – 3 sec2 30° is :- a)o
- b)1
- c)12
- d)8
Correct answer is option 'A'. Can you explain this answer?
The value of 2 tan2 60° – 4 cos2 45° – 3 sec2 30° is :
a)
o
b)
1
c)
12
d)
8
|
Ananya Das answered |
Step-by-step explanation:
2tan2 60° - 4 cos2 45° -3sec2 30° ----(1)
tan 60° = √3
cos 45° = 1/√2
sec 30° = 2/√3
putting value in equation (1)
2(√3)2 - 4(1/√2)2 - 3(2/√3)2
=2(3) - 4(1/2) - 3(4/3)
=6-2-4
=6-6
=0 ANS
If sin A = 1/2, then the value of cot A is
- a)√3
- b)1/√3
- c)√3/2
- d)1
Correct answer is option 'A'. Can you explain this answer?
If sin A = 1/2, then the value of cot A is
a)
√3
b)
1/√3
c)
√3/2
d)
1
|
|
Anushka Budhial answered |
Here is the solution to your question:
So, Correct Answer is Option A
P.S. You can understand all the concepts of Class 10 Trigonometry by going through the chapters:
1. Introduction to Trigonometry:
2. Some Applications of Trigonometry:
The values of x and y which make the following solutions true are: cos x° = sin 52° and cos y° = sin (y° + 10)- a)x = 52°, y = 30°
- b)x = 38°, y = 40°
- c)x = 48°, y = 52°
- d)x = 40°, y = 50°
Correct answer is option 'B'. Can you explain this answer?
The values of x and y which make the following solutions true are: cos x° = sin 52° and cos y° = sin (y° + 10)
a)
x = 52°, y = 30°
b)
x = 38°, y = 40°
c)
x = 48°, y = 52°
d)
x = 40°, y = 50°
|
Ajit mukherjee answered |
Unfortunately, there is incomplete information provided in the question. Please provide the full question for an accurate answer.
A tree is broken by the wind. Its top struck the ground at an angle 30° at a distance of 30 m from its foot. The whole height of the tree is :- a)10 √3 m
- b)20 √3 m
- c)40 √3 m
- d)30 √3 m .
Correct answer is option 'D'. Can you explain this answer?
A tree is broken by the wind. Its top struck the ground at an angle 30° at a distance of 30 m from its foot. The whole height of the tree is :
a)
10 √3 m
b)
20 √3 m
c)
40 √3 m
d)
30 √3 m .
|
|
Sarangi sharma answered |
Degrees from the vertical. The broken section of the tree makes an angle of 60 degrees with the ground. What is the height of the tree before it was broken?
Let's call the height of the tree "h" and the distance from the base of the tree to where it broke "x". We can use trigonometry to solve for these values.
First, we can use the angle of 30 degrees to find the length of the broken section of the tree, which we'll call "y". Using the sine function:
sin(30) = y/h
y = h*sin(30)
y = 0.5h
Next, we can use the angle of 60 degrees and the Pythagorean theorem to find the length of the entire broken section of the tree (including the part still standing). Let's call this length "z".
cos(60) = x/z
z = x/cos(60)
z = 2x
Using the Pythagorean theorem:
z^2 = y^2 + h^2
(2x)^2 = (0.5h)^2 + h^2
4x^2 = 0.25h^2 + h^2
4x^2 = 1.25h^2
h^2 = 4x^2/1.25
h^2 = 3.2x^2
h = sqrt(3.2)x
So the height of the tree before it was broken is equal to the square root of 3.2 times the distance from the base to where it broke. We don't have a specific value for x, so we can't give an exact height, but we can say that it's proportional to the square root of 3.2x.
Let's call the height of the tree "h" and the distance from the base of the tree to where it broke "x". We can use trigonometry to solve for these values.
First, we can use the angle of 30 degrees to find the length of the broken section of the tree, which we'll call "y". Using the sine function:
sin(30) = y/h
y = h*sin(30)
y = 0.5h
Next, we can use the angle of 60 degrees and the Pythagorean theorem to find the length of the entire broken section of the tree (including the part still standing). Let's call this length "z".
cos(60) = x/z
z = x/cos(60)
z = 2x
Using the Pythagorean theorem:
z^2 = y^2 + h^2
(2x)^2 = (0.5h)^2 + h^2
4x^2 = 0.25h^2 + h^2
4x^2 = 1.25h^2
h^2 = 4x^2/1.25
h^2 = 3.2x^2
h = sqrt(3.2)x
So the height of the tree before it was broken is equal to the square root of 3.2 times the distance from the base to where it broke. We don't have a specific value for x, so we can't give an exact height, but we can say that it's proportional to the square root of 3.2x.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 60°. If one strip is exactly behind the other on the same side of the light-house then the distance between the two ships is :- a)25 √3 m
- b)75 √3 m
- c)50 √3 m
- d)None of these.
Correct answer is option 'C'. Can you explain this answer?
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 60°. If one strip is exactly behind the other on the same side of the light-house then the distance between the two ships is :
a)
25 √3 m
b)
75 √3 m
c)
50 √3 m
d)
None of these.
|
|
Pooja Shah answered |
Height of lighthouse =75m
Angles are 30 and 60
Let x be the distance between the ships and y be the distance between the foot of the lighthouse and closer ship.
So tan 60=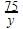
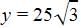
Tan 30 =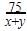
x =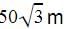
Angles are 30 and 60
Let x be the distance between the ships and y be the distance between the foot of the lighthouse and closer ship.
So tan 60=
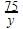
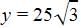
Tan 30 =
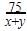
x =
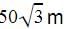
The value of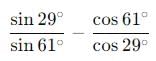 
is :
- a)Zero
- b)1
- c)61/29
- d)29/61
Correct answer is option 'A'. Can you explain this answer?
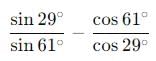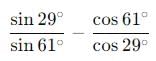The value of is :
is :a)
Zero
b)
1
c)
61/29
d)
29/61
|
|
💕Khushi... 💕 answered |
A. is ri8
Sin29/Sin61-Cos61/Cos29
=>sin29/sin61-cos(90-29)/cos(90-61)
=>sin29/sin61-sin29/sin61
=0
Sin29/Sin61-Cos61/Cos29
=>sin29/sin61-cos(90-29)/cos(90-61)
=>sin29/sin61-sin29/sin61
=0
If 7sin2x + 3cos2x = 4 then , secx + cosecx =- a)
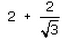
- b)
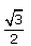
- c)
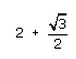
- d)
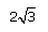
Correct answer is 'A'. Can you explain this answer?
If 7sin2x + 3cos2x = 4 then , secx + cosecx =
a)
b)
c)
d)
|
Naina Sharma answered |
7sin2x+3cos2 x=4
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=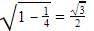
Sec x= 1/cos x=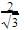
Cosec x + sec x=2+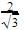
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=
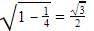
Sec x= 1/cos x=
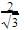
Cosec x + sec x=2+
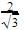
Read the following text and answer the following question on the basis of the same:Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.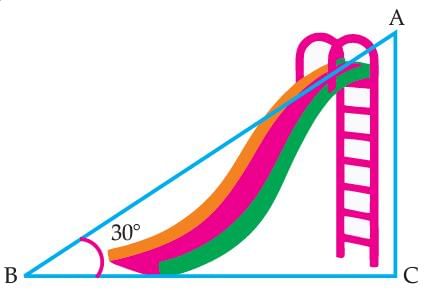
Q. The value of sin2 30° + cos2 60° is: - a)1 / 4
- b)1 / 2
- c)3 / 4
- d)3 / 2
Correct answer is option 'B'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
Q. The value of sin2 30° + cos2 60° is:
a)
1 / 4
b)
1 / 2
c)
3 / 4
d)
3 / 2
|
|
Ishan Choudhury answered |
Sin2 30° + cos2 60°
= (1 / 2)2 + (1 / 2)2
= 1 / 4 + 1 / 4
= 2 / 4 = 1 / 2
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
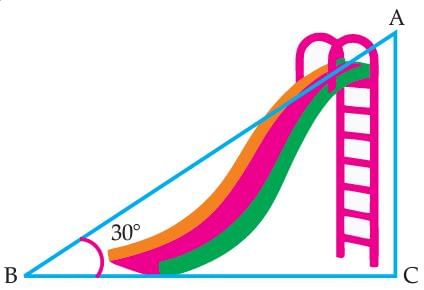Q. The distance of AB is :
- a)8 m
- b)6 m
- c)5 m
- d)10 m
Correct answer is option 'A'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
Q. The distance of AB is :
a)
8 m
b)
6 m
c)
5 m
d)
10 m
|
|
Avinash Patel answered |
We have,
∠B = 30° and AC = 4 m
sinθ=p/h or perpendicular/hypotenuse [perpendicular = side directly in front of θ ]
Then, sin 30° = AC / AB
⇒ 1 / 2 = 4 / AB
⇒ AB = 8 m.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. The length of the string is:- a)40 √3 m
- b)30 m
- c)20 √3 m
- d)60 √3 m.
Correct answer is option 'A'. Can you explain this answer?
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. The length of the string is:
a)
40 √3 m
b)
30 m
c)
20 √3 m
d)
60 √3 m.
|
shekhar Chauhan answered |
Which of the following identities is correct?- a)sin A × tan A = cos A
- b)tan A = sin A / cos A
- c)sec A = 1 / sin A
- d)cos A = 1 / cosec A
Correct answer is option 'B'. Can you explain this answer?
Which of the following identities is correct?
a)
sin A × tan A = cos A
b)
tan A = sin A / cos A
c)
sec A = 1 / sin A
d)
cos A = 1 / cosec A
|
Aryan Pillai answered |
Understanding Trigonometric Identities
In trigonometry, various identities help us simplify and solve problems. Let's evaluate the given options to find the correct identity.
Option A: sin A × tan A = cos A
- This identity is incorrect.
- The tangent function is defined as tan A = sin A / cos A, so the left side does not equal cos A.
Option B: tan A = sin A / cos A
- This identity is correct.
- The tangent function is defined in terms of sine and cosine.
- Hence, tan A = sin A / cos A accurately represents the relationship between these three functions.
Option C: sec A = 1 / sin A
- This identity is incorrect.
- The secant function is defined as sec A = 1 / cos A, not sine.
Option D: cos A = 1 / cosec A
- This identity is also incorrect.
- The cosecant function is defined as cosec A = 1 / sin A, so cos A cannot equal 1 / cosec A.
Conclusion
- The only correct identity among the options is option B: tan A = sin A / cos A.
- This fundamental relationship is essential in trigonometry and is widely used in various calculations and proofs.
In trigonometry, various identities help us simplify and solve problems. Let's evaluate the given options to find the correct identity.
Option A: sin A × tan A = cos A
- This identity is incorrect.
- The tangent function is defined as tan A = sin A / cos A, so the left side does not equal cos A.
Option B: tan A = sin A / cos A
- This identity is correct.
- The tangent function is defined in terms of sine and cosine.
- Hence, tan A = sin A / cos A accurately represents the relationship between these three functions.
Option C: sec A = 1 / sin A
- This identity is incorrect.
- The secant function is defined as sec A = 1 / cos A, not sine.
Option D: cos A = 1 / cosec A
- This identity is also incorrect.
- The cosecant function is defined as cosec A = 1 / sin A, so cos A cannot equal 1 / cosec A.
Conclusion
- The only correct identity among the options is option B: tan A = sin A / cos A.
- This fundamental relationship is essential in trigonometry and is widely used in various calculations and proofs.
Solve: (Sin 30°+cos 60°)-(sin 60° + cos 30°) is equal to:- a)0
- b)1+2√3
- c)1-√3
- d)1+√3
Correct answer is option 'C'. Can you explain this answer?
Solve: (Sin 30°+cos 60°)-(sin 60° + cos 30°) is equal to:
a)
0
b)
1+2√3
c)
1-√3
d)
1+√3
|
Kds Coaching answered |
Answer: (c) 1-√3
Explanation: sin 30° = ½, sin 60° = √3/2, cos 30° = √3/2 and cos 60° = ½
Putting these values, we get:
(½+½)-(√3/2+√3/2)
= 1 – [(2√3)/2]
= 1 – √3
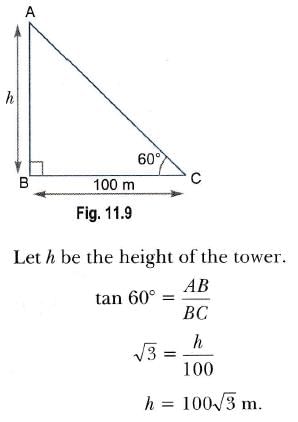
Read the following text and answer the following question on the basis of the same:'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.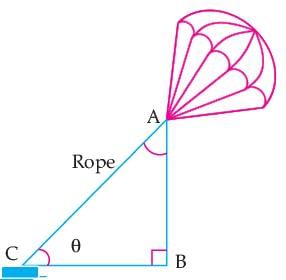
Q. What should be the length of the rope of the kite sail in order to pull the ship at the angle θ and be at a vertical height of 200 m?- a)400 m
- b)300 m
- c)100 m
- d)200 m
Correct answer is option 'A'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.
Q. What should be the length of the rope of the kite sail in order to pull the ship at the angle θ and be at a vertical height of 200 m?
a)
400 m
b)
300 m
c)
100 m
d)
200 m
|
|
Rohit Sharma answered |
In ΔABC, we have
θ = 30°, AB = 200 m
Then, sin 30° = Perpendicular / Hypotenuse
= AB / AC
⇒ 1 / 2 = 200 / AC
⇒ AC = 400 m.
Read the following text and answer the following question on the basis of the same:'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.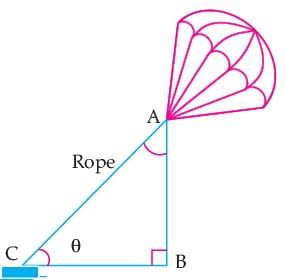
Q. If cos A = 1/ 2 , then the value of 9 cot2 A – 1 is:- a)1
- b)3
- c)2
- d)4
Correct answer is option 'C'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.
Q. If cos A = 1/ 2 , then the value of 9 cot2 A – 1 is:
a)
1
b)
3
c)
2
d)
4
|
|
Naina Sharma answered |
Given, cos A = 1/ 2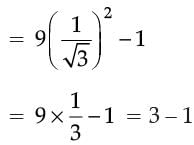
⇒ cos A = cos 60°
⇒ A = 60°
Then, 9 cot2 A – 1 = 9(cot 60°)2 – 1
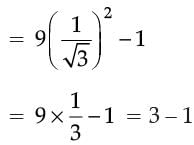
= 2
Chapter doubts & questions for Introduction to Trigonometry - 6 Months Boards Preparation for Class 10 (CBSE) 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Introduction to Trigonometry - 6 Months Boards Preparation for Class 10 (CBSE) in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
6 Months Boards Preparation for Class 10 (CBSE)
344 videos|2427 docs|372 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup