All Exams >
Civil Engineering (CE) >
6 Months Preparation for GATE Civil Engg >
All Questions
All questions of Buoyancy & Floatation for Civil Engineering (CE) Exam
A wooden cylinder of sp.gr. = 0.6 and circular in cross-section is required to float in oil(sp.gr. = 0.90). Find the L/D ratio for the cylinder to float with its longitudinal axis vertical in oil, where L is the height of cylinder and D is its diameter.
- a) L/D<9/16
- b) L/D<3/4
- c) L/D<2/3
- d) None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
A wooden cylinder of sp.gr. = 0.6 and circular in cross-section is required to float in oil(sp.gr. = 0.90). Find the L/D ratio for the cylinder to float with its longitudinal axis vertical in oil, where L is the height of cylinder and D is its diameter.
a)
L/D<9/16b)
L/D<3/4c)
L/D<2/3d)
None of the mentioned|
|
Rajeev Menon answered |
By principle of buoyancy,
Weight of cylinder = Weight of water displaced
h=2L/3
AG=L/2
AB=L/3
BG=AG-AB=L/6
GM= Metacentric height=I/∀ – BG=3D2/32L-L/6
For stable equilibrium, GM should be positive
GM>0
i.e L/D<3/4.
If the magnitude of dimension of a rectangular wooden block is length>breadth>height, then for it to float on the water, it should be immersed in what manner?
- a)It should be immersed horizontally such that breadth is partially immersed
- b)It should be immersed such that height is partially immersed
- c)It should be immersed vertically such that length is partially immersed
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
If the magnitude of dimension of a rectangular wooden block is length>breadth>height, then for it to float on the water, it should be immersed in what manner?
a)
It should be immersed horizontally such that breadth is partially immersed
b)
It should be immersed such that height is partially immersed
c)
It should be immersed vertically such that length is partially immersed
d)
None of the mentioned

|
Arnab Saini answered |
When it is immersed in such a manner where height is partially immersed, its stability is most as moment of inertia is most about that axis.
A rectangular pontoon is 5 m long, 3 m wide and 1.40 m high. The depth of immersion of the pontoon is 0.60 m in seawater. If the centre of gravity is 0.7 m above the bottom of the pontoon, determine the metacentric height. The density for seawater = 1045 kg/m3. - a)0.135
- b)0.271
- c)0.543
- d)0.068
Correct answer is option 'A'. Can you explain this answer?
A rectangular pontoon is 5 m long, 3 m wide and 1.40 m high. The depth of immersion of the pontoon is 0.60 m in seawater. If the centre of gravity is 0.7 m above the bottom of the pontoon, determine the metacentric height. The density for seawater = 1045 kg/m3.
a)
0.135
b)
0.271
c)
0.543
d)
0.068

|
Shail Rane answered |
Explanation: BG=Centre of pontoon – Centre of immersed portion=0.7-0.3=0.4
Metacentric height=I/∀ -BG
I=bd³/12 = 5*3³/12
∀=5*3*1.4
Metacentric height=0.135 m.
Metacentric height=I/∀ -BG
I=bd³/12 = 5*3³/12
∀=5*3*1.4
Metacentric height=0.135 m.
The metacentric height of a passenger ship is kept water lower than that of a naval or a cargo ship. This is because- a)apparent weight will increase
- b)otherwise it will be in neutral equilibrium
- c)it will decrease the frequency of rolling
- d)otherwise it will sink and get totally immersed
Correct answer is option 'C'. Can you explain this answer?
The metacentric height of a passenger ship is kept water lower than that of a naval or a cargo ship. This is because
a)
apparent weight will increase
b)
otherwise it will be in neutral equilibrium
c)
it will decrease the frequency of rolling
d)
otherwise it will sink and get totally immersed
|
|
Moumita Sharma answered |
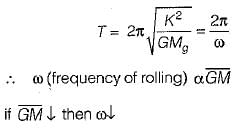
A stone weighs 650 N in air and 275 N in water. Compute its specific gravity.- a)1.73
- b)2.45
- c)3.46
- d)0.865
Correct answer is option 'A'. Can you explain this answer?
A stone weighs 650 N in air and 275 N in water. Compute its specific gravity.
a)
1.73
b)
2.45
c)
3.46
d)
0.865

|
Nilanjan Rane answered |
Explanation: Weight of water displaced=Weight of stone in air – Weight of stone in water
=375
Volume of water displaced=Volume of stone=375/9.81*1000=0.038 m3
Density of stone= mass/volume=650/9.81*0.038=1733 kg/m3
specific gravity= Density of stone/Density of water=1.73.
=375
Volume of water displaced=Volume of stone=375/9.81*1000=0.038 m3
Density of stone= mass/volume=650/9.81*0.038=1733 kg/m3
specific gravity= Density of stone/Density of water=1.73.
Three parallel pipes connected at the two ends have flowrates Q1, Q2, and Q3, respectively, and the corresponding frictional head losses are hL1, hL2, and hL3 respectively. The correct expressions for total flow rate (Q) and frictional head loss across the two ends (hL) are- a)Q = Q1 + Q2 + Q3; hL = hL1 + hL2 + hL3
- b)Q = Q1 + Q2 + Q3; hL = hL1 = hL2 = hL3
- c)Q = Q1 = Q2 = Q3; hL = hL1 + hL2 + hL3
- d)Q = Q1 = Q2 = Q3; hL = hL1 = hL2 = hL3
Correct answer is option 'B'. Can you explain this answer?
Three parallel pipes connected at the two ends have flowrates Q1, Q2, and Q3, respectively, and the corresponding frictional head losses are hL1, hL2, and hL3 respectively. The correct expressions for total flow rate (Q) and frictional head loss across the two ends (hL) are
a)
Q = Q1 + Q2 + Q3; hL = hL1 + hL2 + hL3
b)
Q = Q1 + Q2 + Q3; hL = hL1 = hL2 = hL3
c)
Q = Q1 = Q2 = Q3; hL = hL1 + hL2 + hL3
d)
Q = Q1 = Q2 = Q3; hL = hL1 = hL2 = hL3

|
Constructing Careers answered |
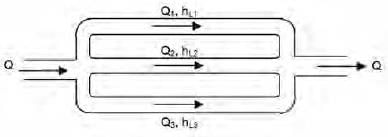
Total flow rate, Q = Q1 + Q2 + Q3 and frictional head loss,
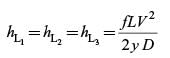
A sprue in a sand mould has a top diameter of 20 mm and height of 200 mm. The velocity of the molten metal at entry of the sprue is 0.5 m/s. Assume acceleration due to gravity as 9.8 m/s2 and neglect all losses. If the mould is well ventilated the velocity (upto 3 decimal points accuracy) of the molten metal at the bottom of the sprue is ____m/s.Correct answer is '2.042'. Can you explain this answer?
A sprue in a sand mould has a top diameter of 20 mm and height of 200 mm. The velocity of the molten metal at entry of the sprue is 0.5 m/s. Assume acceleration due to gravity as 9.8 m/s2 and neglect all losses. If the mould is well ventilated the velocity (upto 3 decimal points accuracy) of the molten metal at the bottom of the sprue is ____m/s.

|
Constructing Careers answered |
Velocity of the molten metal at entry of the sprue V1 = 0.5 m/s
Height h1 = 200 mm
Height h2 = 0
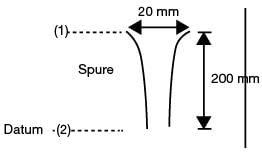
Applying bernaulli’s equation between (1) and (2).
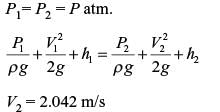
Hence, the correct answer is (2.042).
As a balloon rises in the air its volume increases, at the end it acquires a stable height and cannot rise any further.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
As a balloon rises in the air its volume increases, at the end it acquires a stable height and cannot rise any further.
a)
True
b)
False

|
Jay Menon answered |
Explanation: As balloon rises in air, pressure acting on it reduces and therefore its volume increases. Also, a rising balloon ceases rising when it and the displaced air are equal in weight.
A rectangular block (6m × 3m × 1.2m) is immersed in sea water with depth of immersion 0.8m in water. If the centre of gravity is 0.6 m above the bottom of the block, determine the metacentric height. The density for sea water = 1025 kg/m3- a)0.42 m
- b)0.84 m
- c)0.5 m
- d)0.74 m
Correct answer is option 'D'. Can you explain this answer?
A rectangular block (6m × 3m × 1.2m) is immersed in sea water with depth of immersion 0.8m in water. If the centre of gravity is 0.6 m above the bottom of the block, determine the metacentric height. The density for sea water = 1025 kg/m3
a)
0.42 m
b)
0.84 m
c)
0.5 m
d)
0.74 m

|
Varun Mukherjee answered |
X 4m x 3m) is floating in water with the longer side parallel to the water surface. The density of the block is 1500 kg/m^3. What is the height of the block above the water surface?
The weight of the block can be calculated using the formula:
Weight = Density x Volume x Gravity
The volume of the block can be calculated using the formula:
Volume = Length x Width x Height
Given:
Length = 6m
Width = 4m
Height = ?
Using the volume formula:
Volume = 6m x 4m x Height = 24m^2 x Height
The weight of the block can be calculated as:
Weight = 1500 kg/m^3 x (24m^2 x Height) x 9.8 m/s^2
Since the block is floating, the weight of the block is equal to the buoyant force acting on it. The buoyant force can be calculated using the formula:
Buoyant force = Density of water x Volume of displaced water x Gravity
Since the block is floating, the volume of displaced water is equal to the volume of the block. So:
Buoyant force = Density of water x (24m^2 x Height) x 9.8 m/s^2
Since the buoyant force is equal to the weight of the block, we can set the two equations equal to each other:
1500 kg/m^3 x (24m^2 x Height) x 9.8 m/s^2 = Density of water x (24m^2 x Height) x 9.8 m/s^2
The density of water cancels out on both sides of the equation, leaving:
1500 kg/m^3 x 24m^2 x Height = 24m^2 x Height
Simplifying further:
1500 kg/m^3 x Height = Height
1500 kg/m^3 = 1
Height = 1m
Therefore, the height of the block above the water surface is 1 meter.
The weight of the block can be calculated using the formula:
Weight = Density x Volume x Gravity
The volume of the block can be calculated using the formula:
Volume = Length x Width x Height
Given:
Length = 6m
Width = 4m
Height = ?
Using the volume formula:
Volume = 6m x 4m x Height = 24m^2 x Height
The weight of the block can be calculated as:
Weight = 1500 kg/m^3 x (24m^2 x Height) x 9.8 m/s^2
Since the block is floating, the weight of the block is equal to the buoyant force acting on it. The buoyant force can be calculated using the formula:
Buoyant force = Density of water x Volume of displaced water x Gravity
Since the block is floating, the volume of displaced water is equal to the volume of the block. So:
Buoyant force = Density of water x (24m^2 x Height) x 9.8 m/s^2
Since the buoyant force is equal to the weight of the block, we can set the two equations equal to each other:
1500 kg/m^3 x (24m^2 x Height) x 9.8 m/s^2 = Density of water x (24m^2 x Height) x 9.8 m/s^2
The density of water cancels out on both sides of the equation, leaving:
1500 kg/m^3 x 24m^2 x Height = 24m^2 x Height
Simplifying further:
1500 kg/m^3 x Height = Height
1500 kg/m^3 = 1
Height = 1m
Therefore, the height of the block above the water surface is 1 meter.
When a body, floating in a liquid is given a small angular displacement, it starts oscillating about a point known as- a)center of pressure
- b)center of gravity
- c)center of buoyancy
- d)meta center
Correct answer is option 'D'. Can you explain this answer?
When a body, floating in a liquid is given a small angular displacement, it starts oscillating about a point known as
a)
center of pressure
b)
center of gravity
c)
center of buoyancy
d)
meta center

|
Ameya Sen answered |
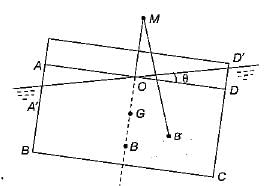
Where M is metacentre and θ is small angle of hill through which a body is tilted.
Hence metacenter is a point about which a body oscillate when tilted or given a small angular displacement.
A cylinder(uniform density distribution) of radius 3.0 m has a height of 9.0 m. The specific gravity of the material of cylinder 0.85 and it is floating in water with its axis vertical. State whether the equilibrium is stable or unstable.- a)Stable
- b)Unstable
- c)Insufficient Data
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
A cylinder(uniform density distribution) of radius 3.0 m has a height of 9.0 m. The specific gravity of the material of cylinder 0.85 and it is floating in water with its axis vertical. State whether the equilibrium is stable or unstable.
a)
Stable
b)
Unstable
c)
Insufficient Data
d)
None of the mentioned

|
Bhaskar Mukherjee answered |
Explanation: BG=Centre of pontoon – Centre of immersed portion=0.3-0.45*0.3=1.65
Metacentric height=I/∀ -BG
I=π*r⁴=π*3⁴
∀=π*r*r*h=π*3*3*9
Metacentric height=0.325.
Metacentric height=I/∀ -BG
I=π*r⁴=π*3⁴
∀=π*r*r*h=π*3*3*9
Metacentric height=0.325.
A floating body attains stable equilibrium if its metacenter is- a)At the centroid
- b)Above the centroid
- c)Below the centroid
- d)Anywhere
Correct answer is option 'B'. Can you explain this answer?
A floating body attains stable equilibrium if its metacenter is
a)
At the centroid
b)
Above the centroid
c)
Below the centroid
d)
Anywhere

|
Bijoy Chauhan answered |
Metacenter and Stable Equilibrium in Floating Bodies
In the context of floating bodies, the metacenter plays a crucial role in determining the stability of the body.
Metacenter
The metacenter is the point at which the vertical line passing through the center of buoyancy of a floating body intersects the centerline of the body when the body is tilted from its equilibrium position. It is a virtual point and does not physically exist on the body.
Stable Equilibrium
A floating body is said to be in stable equilibrium when it returns to its original position after being tilted or disturbed. This means that the body is stable and will not capsize easily.
Position of Metacenter
When the metacenter of a floating body is above the centroid (center of gravity) of the body, the body attains stable equilibrium. This is because when the body is tilted, the metacenter shifts to the new position of the center of buoyancy, which creates a restoring moment that brings the body back to its original position.
Conclusion
In summary, for a floating body to attain stable equilibrium, the metacenter must be located above the centroid of the body. This ensures that the body is stable and will return to its original position when tilted.
In the context of floating bodies, the metacenter plays a crucial role in determining the stability of the body.
Metacenter
The metacenter is the point at which the vertical line passing through the center of buoyancy of a floating body intersects the centerline of the body when the body is tilted from its equilibrium position. It is a virtual point and does not physically exist on the body.
Stable Equilibrium
A floating body is said to be in stable equilibrium when it returns to its original position after being tilted or disturbed. This means that the body is stable and will not capsize easily.
Position of Metacenter
When the metacenter of a floating body is above the centroid (center of gravity) of the body, the body attains stable equilibrium. This is because when the body is tilted, the metacenter shifts to the new position of the center of buoyancy, which creates a restoring moment that brings the body back to its original position.
Conclusion
In summary, for a floating body to attain stable equilibrium, the metacenter must be located above the centroid of the body. This ensures that the body is stable and will return to its original position when tilted.
How can relatively denser object be made to float on the less dense fluid?- a)By altering the shape.
- b)By altering the forces acting on the object
- c)By altering the shear forces acting on the object
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
How can relatively denser object be made to float on the less dense fluid?
a)
By altering the shape.
b)
By altering the forces acting on the object
c)
By altering the shear forces acting on the object
d)
None of the mentioned

|
Jay Menon answered |
Explanation: By changing the shape of an object it can be made to float on a fluid even if it is denser than that fluid. This principle is used in ship building.
A solid cylinder of diameter 4.5 has a height of 2.5 metres. Find the meta-centric height of the cylinder when it is floating in water with its axis vertical. The sp. gr. of the cylinder=0.45.- a)1.9 m
- b)3.8 m
- c)5.7 m
- d).95 m
Correct answer is option 'A'. Can you explain this answer?
A solid cylinder of diameter 4.5 has a height of 2.5 metres. Find the meta-centric height of the cylinder when it is floating in water with its axis vertical. The sp. gr. of the cylinder=0.45.
a)
1.9 m
b)
3.8 m
c)
5.7 m
d)
.95 m

|
Jay Menon answered |
Explanation:BG= Centre of pontoon – Centre of immersed portion=1.25-0.45*2.5=0.125
Metacentric height=I/∀ -BG
I=π*r⁴
∀= π*r*r*h
Metacentric height=1.9 m.
Metacentric height=I/∀ -BG
I=π*r⁴
∀= π*r*r*h
Metacentric height=1.9 m.
If B = Center of buoyancy, G = Center of gravity and M= Metacenter, of afloating body, the body will be in stable equilibrium if- a)MG = 0
- b)M is below G
- c)BG = 0
- d)M is above G
Correct answer is option 'D'. Can you explain this answer?
If B = Center of buoyancy, G = Center of gravity and M= Metacenter, of afloating body, the body will be in stable equilibrium if
a)
MG = 0
b)
M is below G
c)
BG = 0
d)
M is above G
|
|
Akshita Desai answered |
For a floating body
Metacentre above centre of gravity→ Stable Equilibrium
Metacentre coincides centre of gravity→ Neutral Equilibrium
Metacentre below centre of gravity→ Unstable Equilibrium
For a submerged body
Centre of buoyancy above centre of gravity→ Stable Equilibrium
Centre of buoyancy coincides centre of gravity→ Neutral Equilibrium
Centre of buoyancy below centre of gravity→ Unstable Equilibrium
Metacentre above centre of gravity→ Stable Equilibrium
Metacentre coincides centre of gravity→ Neutral Equilibrium
Metacentre below centre of gravity→ Unstable Equilibrium
For a submerged body
Centre of buoyancy above centre of gravity→ Stable Equilibrium
Centre of buoyancy coincides centre of gravity→ Neutral Equilibrium
Centre of buoyancy below centre of gravity→ Unstable Equilibrium
A uniform body of size 4 m long * 2.5 m wide * 1.5 m deep floats in water. What is the weight of the body if depth of immersion is 1.5 m ?
- a)147.1 kN
- b)294.3 kN
- c)73.5 kN
- d)588.6 kN
Correct answer is option 'A'. Can you explain this answer?
A uniform body of size 4 m long * 2.5 m wide * 1.5 m deep floats in water. What is the weight of the body if depth of immersion is 1.5 m ?
a)
147.1 kN
b)
294.3 kN
c)
73.5 kN
d)
588.6 kN

|
Rhea Dasgupta answered |
The weight of a body floating in water can be determined using Archimedes' principle, which states that the buoyant force acting on a body is equal to the weight of the fluid displaced by the body.
In this case, the body is floating in water, so the buoyant force acting on it is equal to its weight. We can calculate the weight of the body using the formula:
Weight = Volume × Density × g
Where:
- Volume is the volume of the body (length × width × depth of immersion)
- Density is the density of water (1000 kg/m³)
- g is the acceleration due to gravity (9.81 m/s²)
Let's calculate the weight of the body step by step:
1. Calculate the volume of the body:
Volume = 4 m × 2.5 m × 1.5 m = 15 m³
2. Calculate the weight:
Weight = Volume × Density × g
= 15 m³ × 1000 kg/m³ × 9.81 m/s²
Converting units:
Weight = 15 m³ × 1000 kg/m³ × 9.81 m/s² / 1000 N/kN
= 147.15 kN
Therefore, the weight of the body is approximately 147.1 kN.
So, the correct answer is option A) 147.1 kN.
In this case, the body is floating in water, so the buoyant force acting on it is equal to its weight. We can calculate the weight of the body using the formula:
Weight = Volume × Density × g
Where:
- Volume is the volume of the body (length × width × depth of immersion)
- Density is the density of water (1000 kg/m³)
- g is the acceleration due to gravity (9.81 m/s²)
Let's calculate the weight of the body step by step:
1. Calculate the volume of the body:
Volume = 4 m × 2.5 m × 1.5 m = 15 m³
2. Calculate the weight:
Weight = Volume × Density × g
= 15 m³ × 1000 kg/m³ × 9.81 m/s²
Converting units:
Weight = 15 m³ × 1000 kg/m³ × 9.81 m/s² / 1000 N/kN
= 147.15 kN
Therefore, the weight of the body is approximately 147.1 kN.
So, the correct answer is option A) 147.1 kN.
A body of dimensions 2.7 m * 3.8 m * 2.5 m, weighs 2500 N in water.Find its weight in air.- a)254.12 kN
- b)508.25 kN
- c)101.65 kN
- d)127.06 kN
Correct answer is option 'A'. Can you explain this answer?
A body of dimensions 2.7 m * 3.8 m * 2.5 m, weighs 2500 N in water.Find its weight in air.
a)
254.12 kN
b)
508.25 kN
c)
101.65 kN
d)
127.06 kN

|
Anisha Chakraborty answered |
Ans.
Option (a)
Weight of stone in air = Weight of water displaced+Weight of stone in water
= 9.81*1000*2.7*3.8*2.5+2500=254.12 kN.
An odd shaped body weighing 7.5 kg and occupying 0.01 m3 volume wiil be completely submerged in a fluid having specific gravity of- a)1
- b)1.2
- c)0.8
- d)0.75
Correct answer is option 'D'. Can you explain this answer?
An odd shaped body weighing 7.5 kg and occupying 0.01 m3 volume wiil be completely submerged in a fluid having specific gravity of
a)
1
b)
1.2
c)
0.8
d)
0.75
|
|
Aniket Saini answered |
Submergence of Odd Shaped Body in Fluid
Given:
Weight of the body, W = 7.5 kg
Volume of the body, V = 0.01 m3
Specific gravity of the fluid, S.G. = ρ/ρw
where, ρ = Density of the fluid
ρw = Density of water
a) If S.G. = 1
Density of water, ρw = 1000 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
As the weight of the body (7.5 kg) is less than the weight of the displaced water (10 kg), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
b) If S.G. = 1.2
Density of the fluid, ρ = S.G. × ρw = 1.2 × 1000 = 1200 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
c) If S.G. = 0.8
Density of the fluid, ρ = S.G. × ρw = 0.8 × 1000 = 800 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
d) If S.G. = 0.75
Density of the fluid, ρ = S.G. × ρw = 0.75 × 1000 = 750 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will sink and be completely submerged in the fluid. Therefore, the correct answer is option 'D'.
Given:
Weight of the body, W = 7.5 kg
Volume of the body, V = 0.01 m3
Specific gravity of the fluid, S.G. = ρ/ρw
where, ρ = Density of the fluid
ρw = Density of water
a) If S.G. = 1
Density of water, ρw = 1000 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
As the weight of the body (7.5 kg) is less than the weight of the displaced water (10 kg), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
b) If S.G. = 1.2
Density of the fluid, ρ = S.G. × ρw = 1.2 × 1000 = 1200 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
c) If S.G. = 0.8
Density of the fluid, ρ = S.G. × ρw = 0.8 × 1000 = 800 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will float on the surface of the fluid. Therefore, the answer is incorrect.
d) If S.G. = 0.75
Density of the fluid, ρ = S.G. × ρw = 0.75 × 1000 = 750 kg/m3
Weight of the displaced water, WD = V × ρw = 0.01 × 1000 = 10 kg
Buoyancy force acting on the body, FB = WD × g = 10 × 9.81 = 98.1 N
Weight of the body, W = 7.5 × 9.81 = 73.58 N
As the buoyancy force (98.1 N) is greater than the weight of the body (73.58 N), the body will sink and be completely submerged in the fluid. Therefore, the correct answer is option 'D'.
A metal block is thrown into deep lake. As it sinks deeper in water, the buoyant force acting on it- a)increases
- b)remains the same
- c)decreases
- d)first increases and then decreases
Correct answer is option 'B'. Can you explain this answer?
A metal block is thrown into deep lake. As it sinks deeper in water, the buoyant force acting on it
a)
increases
b)
remains the same
c)
decreases
d)
first increases and then decreases
|
|
Sharmila Dasgupta answered |
Buoyant force equals the weight of water which has been displaced by an object.
Since, irrespective of the metal block position, the volume displaced by metal is same, hence, buoyant force remains the same.
Since, irrespective of the metal block position, the volume displaced by metal is same, hence, buoyant force remains the same.
Match the conditions of equilibrium for submerged body:

- a)A – M, B – N, C – P
- b)A – N, B – M, C – P
- c)A – P, B – N, C – M
- d)A – M, B – P, C – N
Correct answer is option 'C'. Can you explain this answer?
Match the conditions of equilibrium for submerged body:


a)
A – M, B – N, C – P
b)
A – N, B – M, C – P
c)
A – P, B – N, C – M
d)
A – M, B – P, C – N

|
Pioneer Academy answered |
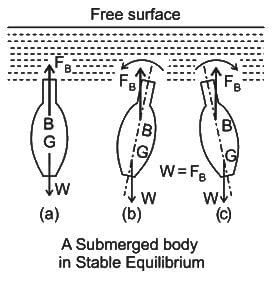
Stability of unconstrained Submerged Bodies in Fluid:
The equilibrium of a body submerged in a liquid requires that the weight of the body acting through its centre of gravity should be colinear with an equal hydrostatic lift acting through the centre of buoyancy.
The equilibrium of a body submerged in a liquid requires that the weight of the body acting through its centre of gravity should be colinear with an equal hydrostatic lift acting through the centre of buoyancy.
- Stable Equilibrium: If the body returns to its original position by retaining the originally vertical axis as vertical
- Unstable Equilibrium: If the body does not return to its original position but moves further from it
- Neutral Equilibrium: If the body neither returns to its original position nor increases its displacement further, it will simply adopt its new position
The relative position of the centre of gravity (G) and centre of buoyancy (B) of a body determines the stability of a submerged body.
Stable Equilibrium: B is above G
Unstable Equilibrium: B is below G
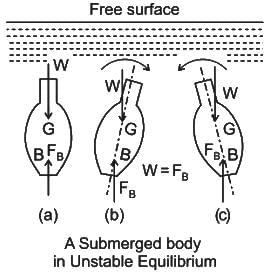
Neutral Equilibrium: B coincides with G
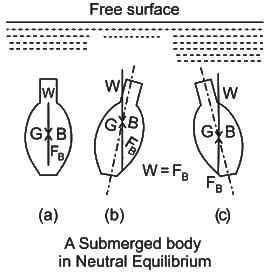
The principle of floatation of bodies is based on the premise of- a)Metacentre
- b)Newtons first law
- c)Newtons law of viscosity
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
The principle of floatation of bodies is based on the premise of
a)
Metacentre
b)
Newtons first law
c)
Newtons law of viscosity
d)
None of the mentioned

|
Navya Kaur answered |
The principle of floatation of bodies is based on the premise of the metacentre. When a body is placed in a fluid, such as water, it experiences an upward buoyant force that is equal to the weight of the fluid displaced by the body. This buoyant force allows the body to float.
Metacentre - the point at which a body immersed in a fluid experiences a restoring force when it is displaced from its equilibrium position.
Understanding the principle of floatation:
1. Buoyant force:
- When an object is submerged in a fluid, it displaces an amount of fluid equal to its own weight.
- According to Archimedes' principle, the buoyant force acting on the object is equal to the weight of the fluid displaced by the object.
- This buoyant force acts in an upward direction, opposing the force of gravity acting on the object.
2. Stability and equilibrium:
- The stability of a floating body depends on its ability to return to its original position when it is displaced.
- The metacentre plays a crucial role in determining the stability of a floating body.
- The metacentre is the point of intersection between the vertical line passing through the centre of buoyancy (the centroid of the displaced volume) and the vertical line passing through the centre of gravity of the body.
- When a floating body is in equilibrium, the metacentre lies above the centre of gravity.
- If the body is tilted from its equilibrium position, a couple of forces is created between the centre of buoyancy and the centre of gravity, causing the body to rotate.
- The metacentre acts as a pivot point for this rotation, providing stability to the body.
3. Metacentric height:
- The distance between the metacentre and the centre of gravity of a floating body is known as the metacentric height.
- A greater metacentric height indicates greater stability, as it increases the lever arm for the rotational forces.
- Stability can be improved by either increasing the metacentric height or lowering the centre of gravity of the body.
Conclusion:
The principle of floatation is based on the metacentre, which provides stability to a floating body. The metacentre acts as a pivot point for rotational forces, allowing the body to return to its equilibrium position when displaced. Understanding the metacentric height is crucial in designing and analyzing the stability of floating structures.
Metacentre - the point at which a body immersed in a fluid experiences a restoring force when it is displaced from its equilibrium position.
Understanding the principle of floatation:
1. Buoyant force:
- When an object is submerged in a fluid, it displaces an amount of fluid equal to its own weight.
- According to Archimedes' principle, the buoyant force acting on the object is equal to the weight of the fluid displaced by the object.
- This buoyant force acts in an upward direction, opposing the force of gravity acting on the object.
2. Stability and equilibrium:
- The stability of a floating body depends on its ability to return to its original position when it is displaced.
- The metacentre plays a crucial role in determining the stability of a floating body.
- The metacentre is the point of intersection between the vertical line passing through the centre of buoyancy (the centroid of the displaced volume) and the vertical line passing through the centre of gravity of the body.
- When a floating body is in equilibrium, the metacentre lies above the centre of gravity.
- If the body is tilted from its equilibrium position, a couple of forces is created between the centre of buoyancy and the centre of gravity, causing the body to rotate.
- The metacentre acts as a pivot point for this rotation, providing stability to the body.
3. Metacentric height:
- The distance between the metacentre and the centre of gravity of a floating body is known as the metacentric height.
- A greater metacentric height indicates greater stability, as it increases the lever arm for the rotational forces.
- Stability can be improved by either increasing the metacentric height or lowering the centre of gravity of the body.
Conclusion:
The principle of floatation is based on the metacentre, which provides stability to a floating body. The metacentre acts as a pivot point for rotational forces, allowing the body to return to its equilibrium position when displaced. Understanding the metacentric height is crucial in designing and analyzing the stability of floating structures.
In unstable equilibrium what is the relation between forces?- a)Buoyancy force= Weight of body
- b)Buoyancy force > Weight of body
- c)Buoyancy force < Weight of body
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
In unstable equilibrium what is the relation between forces?
a)
Buoyancy force= Weight of body
b)
Buoyancy force > Weight of body
c)
Buoyancy force < Weight of body
d)
None of the mentioned

|
Ashwin Gupta answered |
Explanation: Fb=W and the the centre of buoyancy is below the centre of gravity.
Proper explanation for metacentre is:- a)Point at which line of action of force meets the normal axis of body when it is given angular displacement
- b)Intersection of line passing through new centre of buoyancy and centre of gravity.
- c)point about which body starts oscillating when it is given small angular displacement
- d)All of the mentioned
Correct answer is option 'D'. Can you explain this answer?
Proper explanation for metacentre is:
a)
Point at which line of action of force meets the normal axis of body when it is given angular displacement
b)
Intersection of line passing through new centre of buoyancy and centre of gravity.
c)
point about which body starts oscillating when it is given small angular displacement
d)
All of the mentioned

|
Shail Rane answered |
Explanation: All of the above explanation are apt.
When body is completely or partially immersed in a fluid, how much its weight be distributed for it to be in stable equilibrium.- a)Around the lower part
- b)Around the upper part
- c)Is independent of weight distribution
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
When body is completely or partially immersed in a fluid, how much its weight be distributed for it to be in stable equilibrium.
a)
Around the lower part
b)
Around the upper part
c)
Is independent of weight distribution
d)
None of the mentioned

|
Arnab Saini answered |
Explanation: When the weight distribution is around the lower part, the centre of gravity is at lower portion and hence below the centre of buoyancy which is condition for stable equilibrium.
When a ship enters sea from a river one can expect it- a)to rise a little
- b)to sink a little
- c)to remain at the same level of draft
- d)to rise or fall depending on whether it is of wood or steel
Correct answer is option 'A'. Can you explain this answer?
When a ship enters sea from a river one can expect it
a)
to rise a little
b)
to sink a little
c)
to remain at the same level of draft
d)
to rise or fall depending on whether it is of wood or steel
|
|
Harshad Chakraborty answered |
Explanation:
When a ship enters the sea from a river, it experiences a change in the density of the water it is floating on. This change in density is due to the difference in salinity levels between river water and sea water.
• River water is typically less dense than seawater because it has a lower salinity level.
• Sea water, on the other hand, has a higher salinity level, which makes it more dense.
As a result, when a ship enters the sea from a river, it will experience a slight increase in buoyancy due to the higher density of the seawater. This increase in buoyancy will cause the ship to rise a little in the water.
It is important to note that the amount of rise will depend on the size and weight of the ship, as well as the salinity levels of the river and sea water. However, in general, ships can expect to rise a little when entering the sea from a river.
When a ship enters the sea from a river, it experiences a change in the density of the water it is floating on. This change in density is due to the difference in salinity levels between river water and sea water.
• River water is typically less dense than seawater because it has a lower salinity level.
• Sea water, on the other hand, has a higher salinity level, which makes it more dense.
As a result, when a ship enters the sea from a river, it will experience a slight increase in buoyancy due to the higher density of the seawater. This increase in buoyancy will cause the ship to rise a little in the water.
It is important to note that the amount of rise will depend on the size and weight of the ship, as well as the salinity levels of the river and sea water. However, in general, ships can expect to rise a little when entering the sea from a river.
The metacentric height is affected by the change in density.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
The metacentric height is affected by the change in density.
a)
True
b)
False

|
Poulomi Patel answered |
Explanation: Metacentre does depend on the density. Hence, the metacentric height is affected by the change in density.
Meta centre always lies below the centre of gravity- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Meta centre always lies below the centre of gravity
a)
True
b)
False

|
Bhaskar Mukherjee answered |
Explanation: It depends on the stability of floating body.
A solid cylinder of 15 cm diameter and 40 cm long, consists of two parts made of different materials. The first part at the base is 1.5 cm long and of specific gravity = 6.5. The other part of the cylinder is made of the material having specific gravity 0.75. State, if the it can float vertically in water.- a)It will float
- b)It will not float
- c)Data insufficient
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
A solid cylinder of 15 cm diameter and 40 cm long, consists of two parts made of different materials. The first part at the base is 1.5 cm long and of specific gravity = 6.5. The other part of the cylinder is made of the material having specific gravity 0.75. State, if the it can float vertically in water.
a)
It will float
b)
It will not float
c)
Data insufficient
d)
None of the mentioned

|
Gauri Roy answered |
To determine whether the solid cylinder can float vertically in water, we need to compare the weight of the cylinder to the buoyant force acting on it. The buoyant force is equal to the weight of the water displaced by the cylinder.
Given:
Diameter of the cylinder = 15 cm
Length of the cylinder = 40 cm
Length of the first part (base) = 1.5 cm
Specific gravity of the first part = 6.5
Specific gravity of the second part = 0.75
Let's calculate the volume and weight of each part separately and then determine the total weight of the cylinder.
1. Calculation for the first part:
- Diameter of the first part = 15 cm
- Length of the first part = 1.5 cm
- Radius of the first part = diameter/2 = 15/2 = 7.5 cm = 0.075 m
- Volume of the first part = π * (radius^2) * length = π * (0.075^2) * 1.5 = 0.0265 m^3
- Weight of the first part = density * volume * gravity = specific gravity * density of water * volume * gravity = 6.5 * 1000 kg/m^3 * 0.0265 m^3 * 9.8 m/s^2 = 1697.45 N
2. Calculation for the second part:
- Diameter of the second part = 15 cm
- Length of the second part = Total length - Length of the first part = 40 cm - 1.5 cm = 38.5 cm = 0.385 m
- Radius of the second part = diameter/2 = 15/2 = 7.5 cm = 0.075 m
- Volume of the second part = π * (radius^2) * length = π * (0.075^2) * 0.385 = 0.0687 m^3
- Weight of the second part = density * volume * gravity = specific gravity * density of water * volume * gravity = 0.75 * 1000 kg/m^3 * 0.0687 m^3 * 9.8 m/s^2 = 500.565 N
3. Calculation for the total weight of the cylinder:
- Total weight = Weight of the first part + Weight of the second part = 1697.45 N + 500.565 N = 2198.015 N
Now, let's calculate the buoyant force acting on the cylinder:
- Volume of the cylinder = π * (radius^2) * length = π * (0.075^2) * 40 = 0.7071 m^3
- Buoyant force = density of water * volume * gravity = 1000 kg/m^3 * 0.7071 m^3 * 9.8 m/s^2 = 6921.21 N
Since the weight of the cylinder (2198.015 N) is less than the buoyant force (6921.21 N), the cylinder will float vertically in water.
Therefore, the correct answer is option 'A': It will float.
Given:
Diameter of the cylinder = 15 cm
Length of the cylinder = 40 cm
Length of the first part (base) = 1.5 cm
Specific gravity of the first part = 6.5
Specific gravity of the second part = 0.75
Let's calculate the volume and weight of each part separately and then determine the total weight of the cylinder.
1. Calculation for the first part:
- Diameter of the first part = 15 cm
- Length of the first part = 1.5 cm
- Radius of the first part = diameter/2 = 15/2 = 7.5 cm = 0.075 m
- Volume of the first part = π * (radius^2) * length = π * (0.075^2) * 1.5 = 0.0265 m^3
- Weight of the first part = density * volume * gravity = specific gravity * density of water * volume * gravity = 6.5 * 1000 kg/m^3 * 0.0265 m^3 * 9.8 m/s^2 = 1697.45 N
2. Calculation for the second part:
- Diameter of the second part = 15 cm
- Length of the second part = Total length - Length of the first part = 40 cm - 1.5 cm = 38.5 cm = 0.385 m
- Radius of the second part = diameter/2 = 15/2 = 7.5 cm = 0.075 m
- Volume of the second part = π * (radius^2) * length = π * (0.075^2) * 0.385 = 0.0687 m^3
- Weight of the second part = density * volume * gravity = specific gravity * density of water * volume * gravity = 0.75 * 1000 kg/m^3 * 0.0687 m^3 * 9.8 m/s^2 = 500.565 N
3. Calculation for the total weight of the cylinder:
- Total weight = Weight of the first part + Weight of the second part = 1697.45 N + 500.565 N = 2198.015 N
Now, let's calculate the buoyant force acting on the cylinder:
- Volume of the cylinder = π * (radius^2) * length = π * (0.075^2) * 40 = 0.7071 m^3
- Buoyant force = density of water * volume * gravity = 1000 kg/m^3 * 0.7071 m^3 * 9.8 m/s^2 = 6921.21 N
Since the weight of the cylinder (2198.015 N) is less than the buoyant force (6921.21 N), the cylinder will float vertically in water.
Therefore, the correct answer is option 'A': It will float.
Find the position of centre of buoyancy for a wooden block of width 3.5 m and depth 1 m, when it floats horizontally in water. The density of wooden block id 850 kg/m3 and its length 7.0 m. - a)0.95
- b)0.85
- c)1.05
- d)1.65
Correct answer is option 'B'. Can you explain this answer?
Find the position of centre of buoyancy for a wooden block of width 3.5 m and depth 1 m, when it floats horizontally in water. The density of wooden block id 850 kg/m3 and its length 7.0 m.
a)
0.95
b)
0.85
c)
1.05
d)
1.65

|
Jay Menon answered |
Explanation: Weight of the block=ρ*g*Volume=850*9.81*7*3.5*1=204.29 kN
Volume of
water displaced= Weight of water displaced/weight density of water
= 20.825 m3.
h=20.825/3.5*7=0.85 m.
Volume of
water displaced= Weight of water displaced/weight density of water
= 20.825 m3.
h=20.825/3.5*7=0.85 m.
The floating body is said to be in unstable equilibrium if the metacentre is below the centre of gravity.- a)False
- b)True
Correct answer is option 'B'. Can you explain this answer?
The floating body is said to be in unstable equilibrium if the metacentre is below the centre of gravity.
a)
False
b)
True

|
Simran Mukherjee answered |
For a floating body
Metacentre above centre of gravity→ Stable Equilibrium
Metacentre coincides centre of gravity→ Neutral Equilibrium
Metacentre below centre of gravity→ Unstable Equilibrium
For a submerged body
Centre of buoyancy above centre of gravity→ Stable Equilibrium
Centre of buoyancy coincides centre of gravity→ Neutral Equilibrium
Centre of buoyancy below centre of gravity→ Unstable Equilibrium
A solid cylinder of 15 cm diameter and 40 cm long, consists of two parts made of different materials. The first part at the base is 1.5 cm long and of specific gravity=6.5. The other part of the cylinder is made of the material having specific gravity 0.75. State, if the it can float vertically in water.- a)It will float
- b)It will not float
- c)Data insufficient
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
A solid cylinder of 15 cm diameter and 40 cm long, consists of two parts made of different materials. The first part at the base is 1.5 cm long and of specific gravity=6.5. The other part of the cylinder is made of the material having specific gravity 0.75. State, if the it can float vertically in water.
a)
It will float
b)
It will not float
c)
Data insufficient
d)
None of the mentioned

|
Ashwin Gupta answered |
Explanation: AG=(weight of base*distance of C.G from base point A) + (weight of upper part*distance of C.G from point A)/ )weight of base + weight of upper part)
= 14.52
By principle of buoyancy,
Weight of cylinder = Weight of water displaced
h=38.625
AB=19.31
BG=14.25-19.31= -4.79
GM= Metacentric height=I/∀ -BG
= 6.16
As metacentric height is positive, it will float.
= 14.52
By principle of buoyancy,
Weight of cylinder = Weight of water displaced
h=38.625
AB=19.31
BG=14.25-19.31= -4.79
GM= Metacentric height=I/∀ -BG
= 6.16
As metacentric height is positive, it will float.
Submarines use principle of ‘neutral buoyancy’ to go into the water.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Submarines use principle of ‘neutral buoyancy’ to go into the water.
a)
True
b)
False

|
Saptarshi Khanna answered |
Explanation: To dive, the submarine tanks are opened to allow air to exhaust, while the water flows in. When the weight has been balanced so the overall density of the submarine is equal to the water around it, it has neutral buoyancy and hence will go down.
Find the density of metallic body which floats at the interface of mercury of sp.gr 13.6 and water such that 40 % of its volume is sub-merged in mercury and 60% in water.- a)6040 kg/m3
- b)12080 kg/m3
- c)24160 kg/m3
- d)3020 kg/m3
Correct answer is option 'A'. Can you explain this answer?
Find the density of metallic body which floats at the interface of mercury of sp.gr 13.6 and water such that 40 % of its volume is sub-merged in mercury and 60% in water.
a)
6040 kg/m3
b)
12080 kg/m3
c)
24160 kg/m3
d)
3020 kg/m3

|
Jay Menon answered |
Explanation: Total Bouyant force=Force of bouyancy due to water+Force of bouyancy due to mercury
For equilibrium, Total bouyant force= Weiht of body
1000*9.81*0.6*V + 13.6*1000*9.81*0.4*V=ρ*g*V
ρ=6040 kg/m3.
For equilibrium, Total bouyant force= Weiht of body
1000*9.81*0.6*V + 13.6*1000*9.81*0.4*V=ρ*g*V
ρ=6040 kg/m3.
The massless, 1.2 m wide gate shown in fig is pivoted about the frictionless hinge and is held in place by 8896 N counterweight W, Determine the water depth h ______ (m).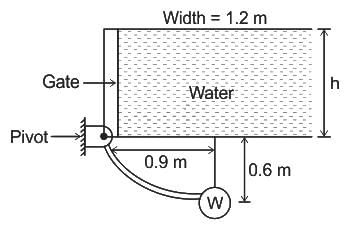
Correct answer is between '1.5,1.7'. Can you explain this answer?
The massless, 1.2 m wide gate shown in fig is pivoted about the frictionless hinge and is held in place by 8896 N counterweight W, Determine the water depth h ______ (m).

|
|
Sanya Agarwal answered |

Now,
∑M0 = 0 for equilibrium.

∴ h = 1.596 m
When body is completely or partially immersed in a fluid, how much its weight be distributed for it to be in stable equilibrium.- a)Around the lower part
- b)Around the upper part
- c)Is independent of weight distribution
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
When body is completely or partially immersed in a fluid, how much its weight be distributed for it to be in stable equilibrium.
a)
Around the lower part
b)
Around the upper part
c)
Is independent of weight distribution
d)
None of the mentioned

|
Rutuja Deshpande answered |
Weight Distribution for Stable Equilibrium in Fluid
Weight distribution in a fluid plays a crucial role in determining the stability of a body immersed in it. When a body is partially or completely immersed in a fluid, its weight must be distributed around the lower part for it to be in stable equilibrium.
Explanation:
- Center of Buoyancy: When a body is immersed in a fluid, it experiences an upward force called buoyancy. This force acts through the center of buoyancy which is the centroid of the volume of fluid displaced by the body.
- Center of Gravity: The weight of the body acts through its center of gravity. For the body to be in stable equilibrium, the center of gravity must be located above the center of buoyancy.
- Stable Equilibrium: When the weight is distributed around the lower part of the body, the center of gravity is positioned below the center of buoyancy. This configuration ensures that any small disturbances will cause the body to return to its original position, maintaining stability.
- Unstable Equilibrium: If the weight is concentrated around the upper part of the body, the center of gravity will be above the center of buoyancy. This leads to an unstable equilibrium where any slight disturbance can cause the body to topple over.
Therefore, to ensure stable equilibrium of a body immersed in a fluid, the weight distribution must be around the lower part to maintain the proper relationship between the center of gravity and the center of buoyancy.
Weight distribution in a fluid plays a crucial role in determining the stability of a body immersed in it. When a body is partially or completely immersed in a fluid, its weight must be distributed around the lower part for it to be in stable equilibrium.
Explanation:
- Center of Buoyancy: When a body is immersed in a fluid, it experiences an upward force called buoyancy. This force acts through the center of buoyancy which is the centroid of the volume of fluid displaced by the body.
- Center of Gravity: The weight of the body acts through its center of gravity. For the body to be in stable equilibrium, the center of gravity must be located above the center of buoyancy.
- Stable Equilibrium: When the weight is distributed around the lower part of the body, the center of gravity is positioned below the center of buoyancy. This configuration ensures that any small disturbances will cause the body to return to its original position, maintaining stability.
- Unstable Equilibrium: If the weight is concentrated around the upper part of the body, the center of gravity will be above the center of buoyancy. This leads to an unstable equilibrium where any slight disturbance can cause the body to topple over.
Therefore, to ensure stable equilibrium of a body immersed in a fluid, the weight distribution must be around the lower part to maintain the proper relationship between the center of gravity and the center of buoyancy.
What happens to the buoyant force acting on the airship as it rises in the air?- a)Buoyant force increases
- b)Buoyant force decreases
- c)Buoyant force remains constant
- d)Buoyant force first increases then shows decrease
Correct answer is option 'B'. Can you explain this answer?
What happens to the buoyant force acting on the airship as it rises in the air?
a)
Buoyant force increases
b)
Buoyant force decreases
c)
Buoyant force remains constant
d)
Buoyant force first increases then shows decrease

|
Jay Menon answered |
Explanation: Buoyant force acting on the airship decreases as it rises in the air as air at higher altitude becomes rarer and its density decreases.
For a completely immersed body, the metacentric height is always zero.- a)Trjue
- b)False
Correct answer is option 'B'. Can you explain this answer?
For a completely immersed body, the metacentric height is always zero.
a)
Trjue
b)
False

|
Poulomi Khanna answered |
False.
Explanation:
Metacentric height is the distance between the center of gravity of a floating body and its metacenter. The metacenter is the point where the vertical line passing through the center of buoyancy intersects the line of action of a small angle of inclination. The metacentric height is an important parameter in the stability analysis of floating bodies.
For a completely immersed body, the center of buoyancy and the center of gravity coincide, and the metacentric height is zero. However, for a floating body, the center of buoyancy and the center of gravity are not the same, and the metacentric height is non-zero. Therefore, the statement is false.
In summary:
- For a completely immersed body, the center of buoyancy and the center of gravity coincide.
- For a floating body, the center of buoyancy and the center of gravity are not the same.
- The metacentric height is the distance between the center of gravity and the metacenter of a floating body.
- The metacentric height is zero for a completely immersed body, but non-zero for a floating body.
Explanation:
Metacentric height is the distance between the center of gravity of a floating body and its metacenter. The metacenter is the point where the vertical line passing through the center of buoyancy intersects the line of action of a small angle of inclination. The metacentric height is an important parameter in the stability analysis of floating bodies.
For a completely immersed body, the center of buoyancy and the center of gravity coincide, and the metacentric height is zero. However, for a floating body, the center of buoyancy and the center of gravity are not the same, and the metacentric height is non-zero. Therefore, the statement is false.
In summary:
- For a completely immersed body, the center of buoyancy and the center of gravity coincide.
- For a floating body, the center of buoyancy and the center of gravity are not the same.
- The metacentric height is the distance between the center of gravity and the metacenter of a floating body.
- The metacentric height is zero for a completely immersed body, but non-zero for a floating body.
A solid cylinder of diameter 5.0 m has a height of 6.0 m. Find the meta-centric height of the cylinder if the specific gravity of the material of cylinder 0.45 and it is floating in water with its axis vertical. State whether the equilibrium is stable or unstable.- a)-0.29 m
- b)-0.61 m
- c)-1.16 m
- d)0.14 m
Correct answer is option 'B'. Can you explain this answer?
A solid cylinder of diameter 5.0 m has a height of 6.0 m. Find the meta-centric height of the cylinder if the specific gravity of the material of cylinder 0.45 and it is floating in water with its axis vertical. State whether the equilibrium is stable or unstable.
a)
-0.29 m
b)
-0.61 m
c)
-1.16 m
d)
0.14 m

|
Anirban Khanna answered |
BG=Centre of pontoon – Centre of immersed portion=0.3-0.45*0.3=1.65
Metacentric height=I/∀ -BG
I=π*r⁴=π*2.5⁴
∀=π*r*r*h=π*2.5*2.5*6
Metacentric height=-0.61.
A floating body is in stable equilibrium when- a)its center of gravity is below the center of buoyancy
- b)its metacentric height is zero
- c)its metacentric height is positive
- d)its metacentric height is negative.
Correct answer is option 'C'. Can you explain this answer?
A floating body is in stable equilibrium when
a)
its center of gravity is below the center of buoyancy
b)
its metacentric height is zero
c)
its metacentric height is positive
d)
its metacentric height is negative.
|
|
Yash Das answered |
For stable equilibrium


What is the principal cause of action of buoyant force on a body submerged partially or fully in fluid?- a)Displacement of fluid due to submerged body
- b)Development of force due to dynamic action
- c)Internal shear forces mitigating external forces
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
What is the principal cause of action of buoyant force on a body submerged partially or fully in fluid?
a)
Displacement of fluid due to submerged body
b)
Development of force due to dynamic action
c)
Internal shear forces mitigating external forces
d)
None of the mentioned

|
Jay Menon answered |
Explanation: The principal cause of action of buoyant force on a body submerged partially or fully in fluid is the force equal in magnitude to the weight of the volume of displaced fluid.
For a completely submerged body with centre of gravity ‘G’ and centre of buoyancy ‘B’, the condition of stability will be- a)G is located below B
- b)G is located above B
- c)G and B are coincident
- d)independent of the locations of G and B
Correct answer is option 'A'. Can you explain this answer?
For a completely submerged body with centre of gravity ‘G’ and centre of buoyancy ‘B’, the condition of stability will be
a)
G is located below B
b)
G is located above B
c)
G and B are coincident
d)
independent of the locations of G and B

|
Swati Dasgupta answered |
At the geometric centre, the buoyant force acting on the body is equal to the weight of the displaced fluid. This is known as Archimedes' principle. The buoyant force is directed upwards, opposing the weight of the body, and the net force acting on the body is zero, resulting in the body floating at a certain level.
If the centre of gravity is not at the geometric centre, the body will have a tendency to rotate until the centre of buoyancy (the centroid of the displaced fluid) is directly below the centre of gravity. This is known as the stable equilibrium position.
If the body is denser than the fluid, it will sink to the bottom. If it is less dense, it will float to the surface. The depth to which a submerged body will sink depends on its density relative to the fluid and the buoyant force acting on it.
If the centre of gravity is not at the geometric centre, the body will have a tendency to rotate until the centre of buoyancy (the centroid of the displaced fluid) is directly below the centre of gravity. This is known as the stable equilibrium position.
If the body is denser than the fluid, it will sink to the bottom. If it is less dense, it will float to the surface. The depth to which a submerged body will sink depends on its density relative to the fluid and the buoyant force acting on it.
The center of buoyancy of a submerged body- a)coincides with the center of gravity of the body
- b)coincides with the centroid of the displaced volume of the fluid
- c)is always below the center of gravity of the body
- d)is always above the centroid of the displaced volume of liquid
Correct answer is option 'B'. Can you explain this answer?
The center of buoyancy of a submerged body
a)
coincides with the center of gravity of the body
b)
coincides with the centroid of the displaced volume of the fluid
c)
is always below the center of gravity of the body
d)
is always above the centroid of the displaced volume of liquid

|
Dipanjan Ghosh answered |
The center of buoyancy is an important concept in fluid mechanics that relates to the stability of submerged bodies. It refers to the point at which the buoyant force acts on a submerged body. The correct answer to this question is option 'B', which states that the center of buoyancy coincides with the centroid of the displaced volume of the fluid.
Explanation:
The center of buoyancy is determined by the shape and position of the submerged body and the density of the fluid in which it is submerged. It is the point at which the upward buoyant force, exerted by the fluid on the body, can be considered to act.
When a body is submerged in a fluid, it displaces a volume of fluid equal to its own volume. This displaced volume is known as the buoyant force. The centroid of this displaced volume is the point where the center of buoyancy is located.
To understand why the center of buoyancy coincides with the centroid of the displaced volume, consider the following:
1. Archimedes' Principle: According to Archimedes' principle, an object immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces. The buoyant force acts vertically upward through the center of buoyancy.
2. Symmetry: For a symmetrically shaped body, such as a rectangular block or a sphere, the center of buoyancy will coincide with the center of gravity. This is because the buoyant force acts vertically upward through the geometric center of the body.
3. Asymmetric Bodies: For bodies with irregular shapes or non-uniform density distributions, the center of buoyancy may not coincide with the center of gravity. In such cases, the center of buoyancy will be located at the centroid of the displaced volume of the fluid. This is because the buoyant force acts through the centroid of the displaced volume, which represents the average position of the fluid that has been displaced.
In summary, the center of buoyancy of a submerged body coincides with the centroid of the displaced volume of the fluid. This concept is crucial in understanding the stability and equilibrium of submerged bodies, especially for engineering applications such as ship design and marine structures.
Explanation:
The center of buoyancy is determined by the shape and position of the submerged body and the density of the fluid in which it is submerged. It is the point at which the upward buoyant force, exerted by the fluid on the body, can be considered to act.
When a body is submerged in a fluid, it displaces a volume of fluid equal to its own volume. This displaced volume is known as the buoyant force. The centroid of this displaced volume is the point where the center of buoyancy is located.
To understand why the center of buoyancy coincides with the centroid of the displaced volume, consider the following:
1. Archimedes' Principle: According to Archimedes' principle, an object immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces. The buoyant force acts vertically upward through the center of buoyancy.
2. Symmetry: For a symmetrically shaped body, such as a rectangular block or a sphere, the center of buoyancy will coincide with the center of gravity. This is because the buoyant force acts vertically upward through the geometric center of the body.
3. Asymmetric Bodies: For bodies with irregular shapes or non-uniform density distributions, the center of buoyancy may not coincide with the center of gravity. In such cases, the center of buoyancy will be located at the centroid of the displaced volume of the fluid. This is because the buoyant force acts through the centroid of the displaced volume, which represents the average position of the fluid that has been displaced.
In summary, the center of buoyancy of a submerged body coincides with the centroid of the displaced volume of the fluid. This concept is crucial in understanding the stability and equilibrium of submerged bodies, especially for engineering applications such as ship design and marine structures.
The buoyant force is- a)equal to volume of liquid displaced
- b)force necessary to maintain equilibrium of a submerged body
- c)the resultant force acting an a floating body
- d)the resultant force on a body due to the fluid surrounding it
Correct answer is option 'D'. Can you explain this answer?
The buoyant force is
a)
equal to volume of liquid displaced
b)
force necessary to maintain equilibrium of a submerged body
c)
the resultant force acting an a floating body
d)
the resultant force on a body due to the fluid surrounding it
|
|
Upasana Gupta answered |
A body submerged in a fluid experiences an upward thrust due to fluid pressure. This force is called buoyant force and a body immersed in a fluid is buoyed or lifted up a force equal to the weight of the fluid displaced by the body. The body apparently loses as much of its weight as the weight of the fluid displaced by it.
An ideal water jet with volume flow rate of 0.05 m3/s strikes a flat plate placed normal to its path and exerts a force of 1000 N. Considering the density of water as 1000 kg/m3, the diameter (in mm) of the water jet is _____Correct answer is '56.4'. Can you explain this answer?
An ideal water jet with volume flow rate of 0.05 m3/s strikes a flat plate placed normal to its path and exerts a force of 1000 N. Considering the density of water as 1000 kg/m3, the diameter (in mm) of the water jet is _____

|
Anmol Choudhary answered |
Understanding the Problem
To find the diameter of the water jet, we need to relate the volume flow rate, the velocity of the jet, and the force exerted by the jet on the flat plate.
Given Data
- Volume flow rate (Q): 0.05 m³/s
- Force exerted (F): 1000 N
- Density of water (ρ): 1000 kg/m³
Calculating Jet Velocity
The momentum principle states that the force exerted by the jet can be expressed as:
F = ρ * Q * V
Where:
- V is the velocity of the jet.
To find the velocity, we can rearrange this equation:
V = F / (ρ * Q)
Substituting the given values:
V = 1000 N / (1000 kg/m³ * 0.05 m³/s)
V = 1000 / 50
V = 20 m/s
Finding the Diameter of the Jet
The volume flow rate is also expressed in terms of the cross-sectional area (A) and velocity (V):
Q = A * V
The cross-sectional area of a circular jet can be calculated as:
A = π * (d/2)²
Substituting for A in the volume flow rate equation:
Q = π * (d/2)² * V
Rearranging to solve for diameter (d):
d = 2 * sqrt(Q / (π * V))
Now, substituting the values:
d = 2 * sqrt(0.05 m³/s / (π * 20 m/s))
d ≈ 0.0564 m or 56.4 mm
Conclusion
Thus, the diameter of the water jet is approximately 56.4 mm.
To find the diameter of the water jet, we need to relate the volume flow rate, the velocity of the jet, and the force exerted by the jet on the flat plate.
Given Data
- Volume flow rate (Q): 0.05 m³/s
- Force exerted (F): 1000 N
- Density of water (ρ): 1000 kg/m³
Calculating Jet Velocity
The momentum principle states that the force exerted by the jet can be expressed as:
F = ρ * Q * V
Where:
- V is the velocity of the jet.
To find the velocity, we can rearrange this equation:
V = F / (ρ * Q)
Substituting the given values:
V = 1000 N / (1000 kg/m³ * 0.05 m³/s)
V = 1000 / 50
V = 20 m/s
Finding the Diameter of the Jet
The volume flow rate is also expressed in terms of the cross-sectional area (A) and velocity (V):
Q = A * V
The cross-sectional area of a circular jet can be calculated as:
A = π * (d/2)²
Substituting for A in the volume flow rate equation:
Q = π * (d/2)² * V
Rearranging to solve for diameter (d):
d = 2 * sqrt(Q / (π * V))
Now, substituting the values:
d = 2 * sqrt(0.05 m³/s / (π * 20 m/s))
d ≈ 0.0564 m or 56.4 mm
Conclusion
Thus, the diameter of the water jet is approximately 56.4 mm.
The metacenter is- a)centroid of the displaced fluid volume
- b)mid point between centre of gravity and centre of Buoyancy
- c)the point of intersection of the line of action of Buoyant force and the centre line of the body
- d)the point of intersection of the line of action of Buoyant force and that of gravitational force
Correct answer is option 'C'. Can you explain this answer?
The metacenter is
a)
centroid of the displaced fluid volume
b)
mid point between centre of gravity and centre of Buoyancy
c)
the point of intersection of the line of action of Buoyant force and the centre line of the body
d)
the point of intersection of the line of action of Buoyant force and that of gravitational force
|
|
Ashwini Ghoshal answered |
Metacenter is the point of inter section of normal axis of the body with the new line of action of buoyant force when body is tilted.
A stone weighs 450 N in air and 200 N in water. Compute the volume of stone.- a).025 m3
- b).05 m3
- c).075 m3
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
A stone weighs 450 N in air and 200 N in water. Compute the volume of stone.
a)
.025 m3
b)
.05 m3
c)
.075 m3
d)
None of the mentioned

|
Anirban Khanna answered |
Weight of water displaced=Weight of stone in air – Weight of stone in water =250
Volume of water displaced=Volume of stone=250/9.81*1000 = 0.025 m^3.
In stable equilibrium for completely submerged bodies what is the relation between forces?- a)Buoyancy force= Weight of body,the centre of buoyancy is below the centre of gravity.
- b)Buoyancy force=Weight of body, the centre of buoyancy is above the centre of gravity.
- c)Buoyancy force < Weight of body
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
In stable equilibrium for completely submerged bodies what is the relation between forces?
a)
Buoyancy force= Weight of body,the centre of buoyancy is below the centre of gravity.
b)
Buoyancy force=Weight of body, the centre of buoyancy is above the centre of gravity.
c)
Buoyancy force < Weight of body
d)
None of the mentioned

|
Mahesh Nair answered |
Explanation: Fb=W and the the centre of buoyancy is above the centre of gravity.
Chapter doubts & questions for Buoyancy & Floatation - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Buoyancy & Floatation - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
6 Months Preparation for GATE Civil Engg
488 videos|1261 docs|878 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup











