All Exams >
Civil Engineering (CE) >
6 Months Preparation for GATE Civil Engg >
All Questions
All questions of Fluid Kinematics for Civil Engineering (CE) Exam
A beaker contains water up to a certain height as shown. If the water is allowed to get discharged through a small pipe (of a uniform diameter), what type of flow will it be in the pipe?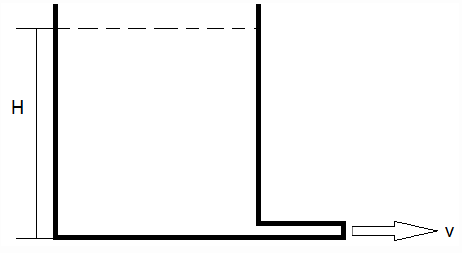
- a)steady and uniform
- b)unsteady and uniform
- c)steady and non-uniform
- d)unsteady and non-uniform
Correct answer is option 'B'. Can you explain this answer?
A beaker contains water up to a certain height as shown. If the water is allowed to get discharged through a small pipe (of a uniform diameter), what type of flow will it be in the pipe?
a)
steady and uniform
b)
unsteady and uniform
c)
steady and non-uniform
d)
unsteady and non-uniform

|
Vertex Academy answered |
Explanation: The velocity in which the water is discharged with a velocity  With time as the water gets discharged,v decreases as H decreases. Hence, it will be an unsteady flow.
With time as the water gets discharged,v decreases as H decreases. Hence, it will be an unsteady flow.
According to the continuity equation, ρAV =constant, where ρ= density, A= cross-sectional area of flow, V = velocity of flow. Since water is treated as an incompressible liquid (ρ =constant) and the pipe has a uniform diameter (A =constant) at a given instant, V will remain constant throughout the whole cross-section of the pipe. Hence, it will be a uniform flow.
According to the continuity equation, ρAV =constant, where ρ= density, A= cross-sectional area of flow, V = velocity of flow. Since water is treated as an incompressible liquid (ρ =constant) and the pipe has a uniform diameter (A =constant) at a given instant, V will remain constant throughout the whole cross-section of the pipe. Hence, it will be a uniform flow.
The characteristic of Ideal fluid are
- a)Incompressible
- b)Fluid velocity is uniform
- c)a and b
- d)Shear stress has a constant, non zero value
Correct answer is option 'C'. Can you explain this answer?
The characteristic of Ideal fluid are
a)
Incompressible
b)
Fluid velocity is uniform
c)
a and b
d)
Shear stress has a constant, non zero value

|
Manasa Sen answered |
As ideal fluid is inviscid, shear stress is zero.
A flow field is defined by the stream function ψ = 2x2 y, determining the corresponding velocity potential.- a) Flow is irrotational, ϕ = 2xy2 − 2 / 3x3 + C
- b) Flow is rotational, ϕ = 2xy2 − 2 / 3x3 + C
- c) Flow is irrotational, ϕ = 2 / 3 x3 − 2xy2 + C
- d) None of the above
Correct answer is option 'D'. Can you explain this answer?
A flow field is defined by the stream function ψ = 2x2 y, determining the corresponding velocity potential.
a)
Flow is irrotational, ϕ = 2xy2 − 2 / 3x3 + C
b)
Flow is rotational, ϕ = 2xy2 − 2 / 3x3 + C
c)
Flow is irrotational, ϕ = 2 / 3 x3 − 2xy2 + C
d)
None of the above

|
Pioneer Academy answered |
Given stream function, ψ = 2x2 y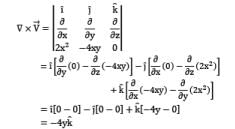
u = ∂ψ / ∂y ; v = − ∂ψ / ∂x ⇒ u = 2x2 ; v = −4xy
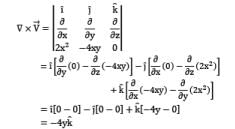
As (∇ ×V ) ≠ 0 ; therefore flow is rotational, and velocity potential function does not exist for rotational flow.
The path taken by the smoke coming out of a chimney (in concentric circles) represents a- a)pathline
- b)streamline
- c)streakline
- d)streamtube
Correct answer is option 'C'. Can you explain this answer?
The path taken by the smoke coming out of a chimney (in concentric circles) represents a
a)
pathline
b)
streamline
c)
streakline
d)
streamtube

|
Gauri Roy answered |
Explanation: A pathline is the path followed by a particle in motion whereas a streamline is an imaginary line within the flow such that the tangent at any point on it indicates the velocity at that point. A streamtube is a collection of streamlines. A streakline is a curve which gives an instantaneous picture of the location of the fluid particleswhich have passed through a given point.
Hence, the path taken by the smoke coming out of a chimney (in concentric circles) will represent streaklines.
Hence, the path taken by the smoke coming out of a chimney (in concentric circles) will represent streaklines.
Which of the following is correct?- a)Pathlines of two particles in an one-dimensional flow can never intersect
- b)Pathlines of two particles in an one-dimensional flow can never intersect if the two particles move along the same direction
- c)Pathlines of two particles in an one-dimensional flow can intersect only if the two particles move along the same direction
- d)Pathlines of two particles in an one-dimensional flow can intersect only if the two particles move along different directions
Correct answer is option 'C'. Can you explain this answer?
Which of the following is correct?
a)
Pathlines of two particles in an one-dimensional flow can never intersect
b)
Pathlines of two particles in an one-dimensional flow can never intersect if the two particles move along the same direction
c)
Pathlines of two particles in an one-dimensional flow can intersect only if the two particles move along the same direction
d)
Pathlines of two particles in an one-dimensional flow can intersect only if the two particles move along different directions
|
|
Sanvi Kapoor answered |
Explanation: The pathline of a particle in an one-dimensional flow is a straight line along the direction it moves. If the two particles move along the same direction, their pathlines will be parallel to each other and will never intersect.
Determine the third velocity component such that continuity equation is satisfied if two components are u=2y2, w=2xyz. - a)-2xy+x2y+f(y,z)
- b)4xy-x2y+f(y,z)
- c)-4xy-x2y+f(y,z)
- d)-2xy-x2y+f(y,z)
Correct answer is option 'C'. Can you explain this answer?
Determine the third velocity component such that continuity equation is satisfied if two components are u=2y2, w=2xyz.
a)
-2xy+x2y+f(y,z)
b)
4xy-x2y+f(y,z)
c)
-4xy-x2y+f(y,z)
d)
-2xy-x2y+f(y,z)

|
Shivam Sharma answered |
The continuity equation for incompressible is du/dx+dv/dy+dw/dz = 0.
Here du/dx=0 and w=2xy.
On solving by integrating, we get v = -4xy-x2y+f(y,z).
Which method is most commonly used in fluid mechanics for analysis?- a)Langragian method
- b)Eulerian Method
- c)Control volume analysis
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Which method is most commonly used in fluid mechanics for analysis?
a)
Langragian method
b)
Eulerian Method
c)
Control volume analysis
d)
None of the mentioned

|
Aarav Chauhan answered |
Explanation: In Eulerian method,we describe velocity, acceleration pressure etc at a point in flow field.hence, it is also most commonly used in fluid mechanics.
When the flow particles flow in zigzag manner and rotate about their own axis it is what type of flow?- a)Turbulent flow
- b)Irrotational flow
- c)Rotational flow
- d)None of the mentioned
Correct answer is option 'D'. Can you explain this answer?
When the flow particles flow in zigzag manner and rotate about their own axis it is what type of flow?
a)
Turbulent flow
b)
Irrotational flow
c)
Rotational flow
d)
None of the mentioned

|
Anisha Chakraborty answered |
Explanation: It is random manner of fluid flow.
A spherical balloon is filled with 3536π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 70π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 50 minutes after the leakage began is- a) 1/9
- b) 1/2
- c) 2/9
- d) 35/18
Correct answer is option 'D'. Can you explain this answer?
A spherical balloon is filled with 3536π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 70π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 50 minutes after the leakage began is
a)
1/9
b)
1/2
c)
2/9
d)
35/18

|
Pioneer Academy answered |

Can the flow inside a nozzle be steady and uniform?- a)yes
- b)never
- c)it can be steady but never uniform
- d)it can be uniform but never steady
Correct answer is option 'C'. Can you explain this answer?
Can the flow inside a nozzle be steady and uniform?
a)
yes
b)
never
c)
it can be steady but never uniform
d)
it can be uniform but never steady

|
Sahana Choudhary answered |
Explanation: According to the continuity equation, ρAV =constant, where ρ= density, A= cross-sectional area of flow, V = velocity of flow. For a nozzle, the area gradually decreases towards it’s exit. Thus, no matter what the rate of flow is, the velocity of flow at the nozzle exit will always be greater than that at it’s entrance. Hence, it’ll always be an unsteady flow. It can be a steady flow if and only if the water level is maintained at a constant level by supplying water at the same rate as it gets discharged, else the water level will keep decreasing with time leading to an unsteady flow.
The velocity potential function of a flow field is given by x2 − y2 + constant. Its stream function will be given by- a) − 2xy + constant
- b) + 2xy + constant
- c) − 2xy + f(x)
- d) − 2xy + f(y)
Correct answer is option 'A'. Can you explain this answer?
The velocity potential function of a flow field is given by x2 − y2 + constant. Its stream function will be given by
a)
− 2xy + constant
b)
+ 2xy + constant
c)
− 2xy + f(x)
d)
− 2xy + f(y)

|
Pioneer Academy answered |
Φ = x2 − y2 + C
∂ϕ / ∂x = −u and ∂ϕ / ∂y = −v
hence u = −2x and v = +2y
Also
∂ψ / ∂y = u ⟹ ∂ψ / ∂y = −2x ⋯ ①
and
∂ψ / ∂x = −v ⟹ ∂ψ / ∂x = −2y ⋯ ②
Partially integrating both the equations ① and ② we get
ψ = −2xy + f(x) + C1 ⋯ ③ and
ψ = −2xy + g(y) + C2 ⋯ ④
respectively.
Since both the equations ③ and ④ are same hence f(x) and g(y) will be zero and C1 = C2
∴ ψ = −2xy + constant.
Local acceleration has constant value for a steady flow.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Local acceleration has constant value for a steady flow.
a)
True
b)
False

|
Anand Kumar answered |
Explanation: Local acceleration is zero for a steady flow.
Obtain the relationship between stream function ψ and the velocity components Vr and Vθ in cylindrical polar coordinates.- a) Vr = − ∂ψ / ∂r and Vθ = 1 /r ∂ψ / ∂θ
- b) Vr = ∂ψ / ∂θ and Vθ = ∂ψ / ∂r
- c) Vr = 1 / r ∂ψ / ∂θ and Vθ = − ∂ψ / ∂r
- d) Vr = ∂ψ / ∂r and Vθ = − 1 / r ∂ψ / ∂θ
Correct answer is option 'C'. Can you explain this answer?
Obtain the relationship between stream function ψ and the velocity components Vr and Vθ in cylindrical polar coordinates.
a)
Vr = − ∂ψ / ∂r and Vθ = 1 /r ∂ψ / ∂θ
b)
Vr = ∂ψ / ∂θ and Vθ = ∂ψ / ∂r
c)
Vr = 1 / r ∂ψ / ∂θ and Vθ = − ∂ψ / ∂r
d)
Vr = ∂ψ / ∂r and Vθ = − 1 / r ∂ψ / ∂θ

|
Jhanvi Choudhary answered |
Understanding the Stream Function in Cylindrical Coordinates
The stream function, denoted as ψ, is a useful concept in fluid dynamics, particularly in cylindrical polar coordinates (r, θ, z). It helps relate the fluid's velocity components to a scalar function, simplifying the analysis of flow fields.
Velocity Components in Cylindrical Coordinates
In cylindrical polar coordinates, the velocity components can be expressed as:
- Vr: Radial velocity component
- Vθ: Angular (or tangential) velocity component
Relationship Between Stream Function and Velocity Components
The correct relationship between the stream function ψ and the velocity components in cylindrical coordinates is given by option 'C':
- Vr = 1/r * ∂ψ / ∂θ
- Vθ = - ∂ψ / ∂r
Explanation of the Relationships
- Radial Velocity (Vr):
- The expression Vr = 1/r * ∂ψ / ∂θ indicates that the radial component of velocity is proportional to the rate of change of the stream function with respect to the angular coordinate θ. This means that as the flow rotates, the radial component is influenced by how the stream function varies in the angular direction.
- Tangential Velocity (Vθ):
- The expression Vθ = - ∂ψ / ∂r shows that the angular component of velocity is inversely related to the rate of change of the stream function with respect to the radial coordinate r. This negative sign indicates that an increase in the radial distance leads to a decrease in the tangential velocity, reflecting the conservation of angular momentum in the flow.
Conclusion
Understanding these relationships is crucial for analyzing fluid flow in cylindrical systems, providing insight into the behavior of the flow field using the stream function.
The stream function, denoted as ψ, is a useful concept in fluid dynamics, particularly in cylindrical polar coordinates (r, θ, z). It helps relate the fluid's velocity components to a scalar function, simplifying the analysis of flow fields.
Velocity Components in Cylindrical Coordinates
In cylindrical polar coordinates, the velocity components can be expressed as:
- Vr: Radial velocity component
- Vθ: Angular (or tangential) velocity component
Relationship Between Stream Function and Velocity Components
The correct relationship between the stream function ψ and the velocity components in cylindrical coordinates is given by option 'C':
- Vr = 1/r * ∂ψ / ∂θ
- Vθ = - ∂ψ / ∂r
Explanation of the Relationships
- Radial Velocity (Vr):
- The expression Vr = 1/r * ∂ψ / ∂θ indicates that the radial component of velocity is proportional to the rate of change of the stream function with respect to the angular coordinate θ. This means that as the flow rotates, the radial component is influenced by how the stream function varies in the angular direction.
- Tangential Velocity (Vθ):
- The expression Vθ = - ∂ψ / ∂r shows that the angular component of velocity is inversely related to the rate of change of the stream function with respect to the radial coordinate r. This negative sign indicates that an increase in the radial distance leads to a decrease in the tangential velocity, reflecting the conservation of angular momentum in the flow.
Conclusion
Understanding these relationships is crucial for analyzing fluid flow in cylindrical systems, providing insight into the behavior of the flow field using the stream function.
Velocity potential function exist only when- a)flow is laminar
- b)flow is turbulent
- c)flow is irrotational
- d)flow is rotational
Correct answer is option 'C'. Can you explain this answer?
Velocity potential function exist only when
a)
flow is laminar
b)
flow is turbulent
c)
flow is irrotational
d)
flow is rotational
|
|
Sanya Agarwal answered |
Velocity Potential Function:
It is defined as the scalar function of space and time, such that its negative derivative with respect to any direction gives the velocity in that direction.
It is denoted by ϕ and defined for two-dimensional as well as three-dimensional flow.
u = −∂ϕ / ∂x; v = −∂ϕ / ∂y; w = −∂ϕ / ∂z
It is defined as the scalar function of space and time, such that its negative derivative with respect to any direction gives the velocity in that direction.
It is denoted by ϕ and defined for two-dimensional as well as three-dimensional flow.
u = −∂ϕ / ∂x; v = −∂ϕ / ∂y; w = −∂ϕ / ∂z
Properties of Stream function:
- If velocity potential function exists, the flow should be irrotational
- If the velocity potential function satisfies the Laplace equation i.e. ∂2ϕ/∂x2 + ∂2ϕ/∂y2 = 0, it is a case of steady incompressible irrotational flow
Which of the following is not an example of free vortex flow?- a)Flow of a water through runner of a turbine
- b)Flow of liquid through a hole provided at the bottom
- c)A whirlpool in a river
- d)Flow of the liquid around a circular bend in a pipe
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not an example of free vortex flow?
a)
Flow of a water through runner of a turbine
b)
Flow of liquid through a hole provided at the bottom
c)
A whirlpool in a river
d)
Flow of the liquid around a circular bend in a pipe

|
Nabanita Saha answered |
Introduction:
Free vortex flow refers to a type of fluid flow in which the fluid particles rotate about a central axis without any radial flow. In this flow pattern, the fluid particles move in concentric circles, and the tangential velocity decreases as the radius increases. The following options are given, and we need to identify the one that is not an example of free vortex flow.
Explanation:
Let's analyze each option and determine if it represents free vortex flow or not.
a) Flow of water through the runner of a turbine:
This option represents the flow of water through the runner of a turbine. In this case, the water enters the turbine with a certain velocity and rotational motion. As it passes through the runner, the water particles follow a curved path and rotate about the central axis. Therefore, this option represents free vortex flow.
b) Flow of liquid through a hole provided at the bottom:
This option describes the flow of liquid through a hole provided at the bottom. When a hole is opened at the bottom of a container filled with liquid, the liquid flows out due to the force of gravity. The liquid particles near the hole move with higher velocity, and the velocity decreases as we move away from the hole. However, the rotational motion of the particles is not significant in this case. Therefore, this option does not represent free vortex flow.
c) A whirlpool in a river:
A whirlpool in a river is a classic example of free vortex flow. It occurs when water flows in a circular path, creating a swirling motion. The water particles rotate about a central axis, and the tangential velocity decreases as the radius increases. Therefore, this option represents free vortex flow.
d) Flow of the liquid around a circular bend in a pipe:
When a liquid flows around a circular bend in a pipe, it experiences a combination of radial and tangential flow. The fluid particles near the inner side of the bend experience a higher velocity and tend to move away from the bend. The fluid particles on the outer side of the bend move slower and tend to move towards the bend. This combination of radial and tangential flow does not represent a pure rotational motion about a central axis, which is characteristic of free vortex flow. Therefore, this option does not represent free vortex flow.
Conclusion:
After analyzing each option, we can conclude that option 'A' (Flow of water through the runner of a turbine) is not an example of free vortex flow. The other options, including the flow of liquid through a hole, a whirlpool in a river, and the flow of liquid around a circular bend in a pipe, all represent free vortex flow in different scenarios.
Free vortex flow refers to a type of fluid flow in which the fluid particles rotate about a central axis without any radial flow. In this flow pattern, the fluid particles move in concentric circles, and the tangential velocity decreases as the radius increases. The following options are given, and we need to identify the one that is not an example of free vortex flow.
Explanation:
Let's analyze each option and determine if it represents free vortex flow or not.
a) Flow of water through the runner of a turbine:
This option represents the flow of water through the runner of a turbine. In this case, the water enters the turbine with a certain velocity and rotational motion. As it passes through the runner, the water particles follow a curved path and rotate about the central axis. Therefore, this option represents free vortex flow.
b) Flow of liquid through a hole provided at the bottom:
This option describes the flow of liquid through a hole provided at the bottom. When a hole is opened at the bottom of a container filled with liquid, the liquid flows out due to the force of gravity. The liquid particles near the hole move with higher velocity, and the velocity decreases as we move away from the hole. However, the rotational motion of the particles is not significant in this case. Therefore, this option does not represent free vortex flow.
c) A whirlpool in a river:
A whirlpool in a river is a classic example of free vortex flow. It occurs when water flows in a circular path, creating a swirling motion. The water particles rotate about a central axis, and the tangential velocity decreases as the radius increases. Therefore, this option represents free vortex flow.
d) Flow of the liquid around a circular bend in a pipe:
When a liquid flows around a circular bend in a pipe, it experiences a combination of radial and tangential flow. The fluid particles near the inner side of the bend experience a higher velocity and tend to move away from the bend. The fluid particles on the outer side of the bend move slower and tend to move towards the bend. This combination of radial and tangential flow does not represent a pure rotational motion about a central axis, which is characteristic of free vortex flow. Therefore, this option does not represent free vortex flow.
Conclusion:
After analyzing each option, we can conclude that option 'A' (Flow of water through the runner of a turbine) is not an example of free vortex flow. The other options, including the flow of liquid through a hole, a whirlpool in a river, and the flow of liquid around a circular bend in a pipe, all represent free vortex flow in different scenarios.
The pattern for streamlines and equipotential lines is different for source and sink flow.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
The pattern for streamlines and equipotential lines is different for source and sink flow.
a)
True
b)
False

|
Aditya Jain answered |
Introduction:
Streamlines and equipotential lines are commonly used in fluid mechanics to visualize the flow pattern and potential distribution in a fluid field. The pattern of these lines varies depending on the type of flow, whether it is a source flow or a sink flow. In this context, the statement claims that the pattern for streamlines and equipotential lines is different for source and sink flow.
Explanation:
To understand why the statement is true, let's first define what source flow and sink flow are:
- Source Flow: In source flow, fluid is flowing outward from a central point, creating a radial flow pattern. It can be visualized as a fluid source that emits fluid particles in all directions.
- Sink Flow: In sink flow, fluid is flowing inward towards a central point, creating a converging flow pattern. It can be visualized as a fluid sink that absorbs fluid particles from all directions.
Now, let's analyze the pattern of streamlines and equipotential lines for each type of flow:
1. Source Flow:
- Streamlines: In source flow, the streamlines are radial lines that originate from the central point and spread outwards. The streamlines are equidistant from each other, indicating a uniform flow rate at every point along the streamlines.
- Equipotential Lines: The equipotential lines in source flow are concentric circles centered at the source point. These lines represent the potential distribution in the flow field. The equipotential lines are perpendicular to the streamlines, indicating that the potential gradient is perpendicular to the flow direction.
2. Sink Flow:
- Streamlines: In sink flow, the streamlines are converging lines that approach the central point. The streamlines become closer to each other as they approach the sink, indicating an increasing flow rate towards the center.
- Equipotential Lines: The equipotential lines in sink flow are also concentric circles centered at the sink point. Similar to source flow, the equipotential lines are perpendicular to the streamlines, indicating the potential gradient direction.
Conclusion:
In conclusion, the pattern for streamlines and equipotential lines is different for source and sink flow. Source flow exhibits radial streamlines and concentric equipotential lines, while sink flow exhibits converging streamlines and concentric equipotential lines. Understanding these patterns is crucial for visualizing and analyzing fluid flow in different scenarios.
Streamlines and equipotential lines are commonly used in fluid mechanics to visualize the flow pattern and potential distribution in a fluid field. The pattern of these lines varies depending on the type of flow, whether it is a source flow or a sink flow. In this context, the statement claims that the pattern for streamlines and equipotential lines is different for source and sink flow.
Explanation:
To understand why the statement is true, let's first define what source flow and sink flow are:
- Source Flow: In source flow, fluid is flowing outward from a central point, creating a radial flow pattern. It can be visualized as a fluid source that emits fluid particles in all directions.
- Sink Flow: In sink flow, fluid is flowing inward towards a central point, creating a converging flow pattern. It can be visualized as a fluid sink that absorbs fluid particles from all directions.
Now, let's analyze the pattern of streamlines and equipotential lines for each type of flow:
1. Source Flow:
- Streamlines: In source flow, the streamlines are radial lines that originate from the central point and spread outwards. The streamlines are equidistant from each other, indicating a uniform flow rate at every point along the streamlines.
- Equipotential Lines: The equipotential lines in source flow are concentric circles centered at the source point. These lines represent the potential distribution in the flow field. The equipotential lines are perpendicular to the streamlines, indicating that the potential gradient is perpendicular to the flow direction.
2. Sink Flow:
- Streamlines: In sink flow, the streamlines are converging lines that approach the central point. The streamlines become closer to each other as they approach the sink, indicating an increasing flow rate towards the center.
- Equipotential Lines: The equipotential lines in sink flow are also concentric circles centered at the sink point. Similar to source flow, the equipotential lines are perpendicular to the streamlines, indicating the potential gradient direction.
Conclusion:
In conclusion, the pattern for streamlines and equipotential lines is different for source and sink flow. Source flow exhibits radial streamlines and concentric equipotential lines, while sink flow exhibits converging streamlines and concentric equipotential lines. Understanding these patterns is crucial for visualizing and analyzing fluid flow in different scenarios.
In a steady state flow, the velocity components are u = 2kx ; v = 2ky ; w = −4kz Find the equation of streamline passing through the point (1, 0, 1).- a) y = 1 / x2 , z = 0
- b) y = 0, z = 1 / x2
- c) y = 0, z = 0
- d) y = 1 / x , z = 1 / x2
Correct answer is option 'B'. Can you explain this answer?
In a steady state flow, the velocity components are u = 2kx ; v = 2ky ; w = −4kz Find the equation of streamline passing through the point (1, 0, 1).
a)
y = 1 / x2 , z = 0
b)
y = 0, z = 1 / x2
c)
y = 0, z = 0
d)
y = 1 / x , z = 1 / x2
|
|
Sanya Agarwal answered |
The streamlines are defined by
dx / u = dy / v = dz / w
Substituting for u, v and w, we obtain
dx / 2kx = dy / 2ky = −dz / 4kz
(a) (b) ©
Consider the expressions (a) and (b) and integrate
∫dx / x = ∫dy/ y
or loge x = loge y + constant which is equivalent to y = C1 x where C1 is a constant.
Likewise expressions (a) and (c) yield,
2∫dx / x = − ∫dz /- y
or loge x2 = − loge z + constant
which is equivalent to z = C2 / x2
where C2 is another constant. All the streamlines in the given flow field are described by equations
y = C1 x and z = C2 / x2 with different values of
C1 and C2
For the streamline passing through the given point (1, 0, 1) the constants C1 and C2 are to be such that y = 0 and z = 1 at x = 1. ∴ C1 = 0 and C2 = 1
Thus the streamline passing through (1, 0, 1) is y = 0 and z = 1 / x2
What is the characteristic of stagnation point- a)Velocity is zero
- b)Acceleration is uniform
- c)Velocity is uniform
- d)Acceleration is zero
Correct answer is option 'A'. Can you explain this answer?
What is the characteristic of stagnation point
a)
Velocity is zero
b)
Acceleration is uniform
c)
Velocity is uniform
d)
Acceleration is zero

|
Prasad Desai answered |
Explanation: At stagnation point velocity is zero, as the fluid comes at rest. This characteristic at stagnation point.
The continuity equation is based on the principle of- a)conservation of mass
- b)conservation of momentum
- c)conservation of energy
- d)conservation of force
Correct answer is option 'A'. Can you explain this answer?
The continuity equation is based on the principle of
a)
conservation of mass
b)
conservation of momentum
c)
conservation of energy
d)
conservation of force
|
|
Sanvi Kapoor answered |
According to the Continuity Equation, if no fluid is added or removed from the pipe in any length then the mass passing across different sections shall be the same. This is in accordance with the principle of conservation of mass which states that matter can neither be created nor be destroyed.
If the streamlines of the particles in a flow are parallel to each other, what type of flow can it be?- a)steady
- b)unsteady
- c)uniform
- d)non-uniform
Correct answer is option 'C'. Can you explain this answer?
If the streamlines of the particles in a flow are parallel to each other, what type of flow can it be?
a)
steady
b)
unsteady
c)
uniform
d)
non-uniform

|
Sreemoyee Chauhan answered |
Explanation: Streamline spacing varies inversely as the velocity. In a uniform flow, the velocities of the particles are the same at every instant of time. Hence, the spacing between their streamlines will be the same. In other words, the streamlines will be parallel.
Uniform flow is defined as the type of flow in which acceleration is zero i.e velocity is constant.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Uniform flow is defined as the type of flow in which acceleration is zero i.e velocity is constant.
a)
True
b)
False

|
Anisha Chakraborty answered |
Explanation: Uniform flow is defined as the type of flow in which the velocity does not change with respect to space. It can change with respect to time.
Which of the following functions are valid velocity potential functions(ϕ)?- a)ϕ = Axy
- b)ϕ = A(x2 - y2)
- c)ϕ = mln(x)
- d)ϕ = cos(x)
Correct answer is option 'A'. Can you explain this answer?
Which of the following functions are valid velocity potential functions(ϕ)?
a)
ϕ = Axy
b)
ϕ = A(x2 - y2)
c)
ϕ = mln(x)
d)
ϕ = cos(x)
|
|
Sanvi Kapoor answered |
Concept:
Valid potential function satisfies the place equation,
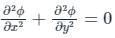
For option 1:
ϕ = Axy
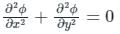
Hence the option 1 is correct
Valid potential function satisfies the place equation,
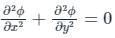
For option 1:
ϕ = Axy
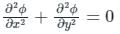
Hence the option 1 is correct
State whether the following flow field is physically possible? u = 3xy2 + 2x + y2 and v = x2 − 2y − y3- a) Possible for steady incompressible rotational flow
- b) Possible for steady incompressible irrotational flow
- c) Possible for steady compressible rotational flow
- d) Possible for steady compressible irrotational flow
Correct answer is option 'A'. Can you explain this answer?
State whether the following flow field is physically possible? u = 3xy2 + 2x + y2 and v = x2 − 2y − y3
a)
Possible for steady incompressible rotational flow
b)
Possible for steady incompressible irrotational flow
c)
Possible for steady compressible rotational flow
d)
Possible for steady compressible irrotational flow

|
Swati Dasgupta answered |
Given flow field: u = 3xy^2 + 2x - y^2 and v = x^2 - 2y - y^3
To determine whether the flow field is physically possible, we need to consider certain properties of the flow field such as continuity equation, irrotational flow, and compressibility.
1. Continuity Equation:
The continuity equation for an incompressible flow is given by ∇ · V = 0, where V is the velocity vector field. Let's calculate ∇ · V for the given flow field:
∇ · V = ∂u/∂x + ∂v/∂y
= (3y^2 + 2) + (2x - 2y - 3y^2)
= 2x - 2y
From the continuity equation, it can be observed that the flow field is incompressible only if ∇ · V = 0. In this case, the flow field is incompressible as the equation evaluates to 2x - 2y.
2. Irrotational Flow:
An irrotational flow field has zero vorticity, which means the curl of the velocity vector field (∇ × V) should be zero. Let's calculate ∇ × V for the given flow field:
∇ × V = (∂v/∂x - ∂u/∂y) i + (∂u/∂x + ∂v/∂y) j
= (-2 + 2x - 6y^2) i + (3y^2 + 2 - 2x) j
From the expression for ∇ × V, it can be observed that the flow field is rotational as it has non-zero vorticity.
3. Compressibility:
To determine compressibility, we need to check if the flow field satisfies the compressible flow equations, which are not given in the question. As the equations are not provided, we cannot determine the compressibility of the flow field.
Conclusion:
Based on the analysis above, we can conclude that the given flow field is possible for steady incompressible rotational flow.
To determine whether the flow field is physically possible, we need to consider certain properties of the flow field such as continuity equation, irrotational flow, and compressibility.
1. Continuity Equation:
The continuity equation for an incompressible flow is given by ∇ · V = 0, where V is the velocity vector field. Let's calculate ∇ · V for the given flow field:
∇ · V = ∂u/∂x + ∂v/∂y
= (3y^2 + 2) + (2x - 2y - 3y^2)
= 2x - 2y
From the continuity equation, it can be observed that the flow field is incompressible only if ∇ · V = 0. In this case, the flow field is incompressible as the equation evaluates to 2x - 2y.
2. Irrotational Flow:
An irrotational flow field has zero vorticity, which means the curl of the velocity vector field (∇ × V) should be zero. Let's calculate ∇ × V for the given flow field:
∇ × V = (∂v/∂x - ∂u/∂y) i + (∂u/∂x + ∂v/∂y) j
= (-2 + 2x - 6y^2) i + (3y^2 + 2 - 2x) j
From the expression for ∇ × V, it can be observed that the flow field is rotational as it has non-zero vorticity.
3. Compressibility:
To determine compressibility, we need to check if the flow field satisfies the compressible flow equations, which are not given in the question. As the equations are not provided, we cannot determine the compressibility of the flow field.
Conclusion:
Based on the analysis above, we can conclude that the given flow field is possible for steady incompressible rotational flow.
A fluid flowing through a pipe of diameter 450 mm with velocity 3 m/s is divided into two pipes of diameters 300 mm and 200 mm. The velocity of flow in 300 mm diameter pipe is 2.5 m/s, then the velocity of flow through 200 mm diameter pipe will be - a)2.5 m/s
- b)5.55 m/s
- c)7.25 m/s
- d)9.56 m/s
Correct answer is option 'D'. Can you explain this answer?
A fluid flowing through a pipe of diameter 450 mm with velocity 3 m/s is divided into two pipes of diameters 300 mm and 200 mm. The velocity of flow in 300 mm diameter pipe is 2.5 m/s, then the velocity of flow through 200 mm diameter pipe will be
a)
2.5 m/s
b)
5.55 m/s
c)
7.25 m/s
d)
9.56 m/s
|
|
Lavanya Menon answered |
Concept:
According to continuity, the liquid flow rate will be conserved.
Q1 = Q2 + Q3
In a pipe, flow rate is given by
Q = AV
Calculation:
Given V1 = 3 m/s, D1 = 450 mm, V2 = 2.5 m/s, D2 = 300 mm, D3 = 200 mm;
From continuity,
D12 V1 = D22 V2 + D32 V3
⇒ 4502 × 3 = 3002 × 2.5 + 2002 × V3
⇒ V3 = 9.56 m/s
According to continuity, the liquid flow rate will be conserved.
Q1 = Q2 + Q3
In a pipe, flow rate is given by
Q = AV
Calculation:
Given V1 = 3 m/s, D1 = 450 mm, V2 = 2.5 m/s, D2 = 300 mm, D3 = 200 mm;
From continuity,
D12 V1 = D22 V2 + D32 V3
⇒ 4502 × 3 = 3002 × 2.5 + 2002 × V3
⇒ V3 = 9.56 m/s
What type of flow can be taken for granted in a pipe of a uniform cross-section?- a)steady
- b)unsteady
- c)uniform
- d)non-uniform
Correct answer is option 'C'. Can you explain this answer?
What type of flow can be taken for granted in a pipe of a uniform cross-section?
a)
steady
b)
unsteady
c)
uniform
d)
non-uniform

|
Arnab Saini answered |
Explanation: According to the continuity equation, ρAV =constant, where ρ= density, A= cross-sectional area of flow, V = velocity of flow. For a pipe of a uniform cross-section, no matter what the rate of flow is, the velocity of flow inside the pipe will always remain constant. Hence, it’ll always be a uniform flow. It’ll be a steady flow if and only if the water level is maintained at a constant level by supplying water at the same rate as it gets discharged, else the water level will keep decreasing with time leading to an unsteady flow.
In potential function, rotational component is:- a)5/2 times vorticity
- b)1/2 times vorticity
- c)3/5 times vorticity
- d)3/2 times vorticity
Correct answer is option 'B'. Can you explain this answer?
In potential function, rotational component is:
a)
5/2 times vorticity
b)
1/2 times vorticity
c)
3/5 times vorticity
d)
3/2 times vorticity
|
|
Tanvi Shah answered |
Vorticity(ξ):
It is defined as the ratio of limiting value of circulation and area of a closed contour. it measures the local rotation of a fluid parcel.
vorticity = Circulation / Area
Vorticity is defined as the twice of the rotational component.
ξ = 2ω,
But,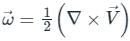
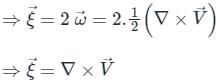
Where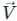 represents velocity field
represents velocity field
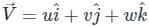
So vorticity is also equal to the curl of the velocity factor.
It is defined as the ratio of limiting value of circulation and area of a closed contour. it measures the local rotation of a fluid parcel.
vorticity = Circulation / Area
Vorticity is defined as the twice of the rotational component.
ξ = 2ω,
But,
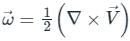
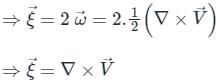
Where
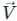 represents velocity field
represents velocity field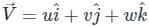
So vorticity is also equal to the curl of the velocity factor.
What is unit for flow rate for gases?- a)m3/s
- b)litres/s
- c)cm3/s
- d)kgf/s
Correct answer is option 'D'. Can you explain this answer?
What is unit for flow rate for gases?
a)
m3/s
b)
litres/s
c)
cm3/s
d)
kgf/s

|
Sharmila Gupta answered |
Flow rate for gases is commonly measured in kgf/s (kilogram-force per second).
Here's an explanation of why the correct answer is option 'D':
Unit Analysis:
To understand why the unit for flow rate of gases is kgf/s, let's break down the units:
- 'kgf' stands for kilogram-force, which is a unit of force.
- 's' stands for seconds, which is a unit of time.
Flow Rate Definition:
Flow rate refers to the amount of gas that passes through a given point in a system per unit time. It is commonly expressed in terms of mass or volume per unit time.
- Mass Flow Rate: This is the amount of gas passing through a point in a system per unit time, measured in kilograms per second (kg/s). It represents the mass of gas flowing per unit time.
- Volume Flow Rate: This is the amount of gas passing through a point in a system per unit time, measured in cubic meters per second (m³/s). It represents the volume of gas flowing per unit time.
Conversion between Mass Flow Rate and Volume Flow Rate:
To convert between mass flow rate and volume flow rate for gases, one needs to consider the gas density. The density of a gas is defined as its mass per unit volume. By multiplying the volume flow rate by the gas density, one can obtain the mass flow rate.
- Mass Flow Rate (kg/s) = Volume Flow Rate (m³/s) × Gas Density (kg/m³)
Explanation of the Correct Answer:
The correct answer, option 'D' (kgf/s), represents the flow rate of gases in terms of force per unit time. The use of kilogram-force (kgf) in this context is due to the historical convention of expressing force in terms of the gravitational force exerted on a mass of one kilogram.
- 1 kgf is defined as the force exerted by gravity on a mass of 1 kilogram.
- The unit kgf/s represents the force per unit time, which is equivalent to the mass flow rate (kg/s) when considering the acceleration due to gravity.
Conclusion:
In summary, the unit for flow rate of gases is kgf/s. This unit represents the force per unit time and is equivalent to the mass flow rate when considering the acceleration due to gravity.
Here's an explanation of why the correct answer is option 'D':
Unit Analysis:
To understand why the unit for flow rate of gases is kgf/s, let's break down the units:
- 'kgf' stands for kilogram-force, which is a unit of force.
- 's' stands for seconds, which is a unit of time.
Flow Rate Definition:
Flow rate refers to the amount of gas that passes through a given point in a system per unit time. It is commonly expressed in terms of mass or volume per unit time.
- Mass Flow Rate: This is the amount of gas passing through a point in a system per unit time, measured in kilograms per second (kg/s). It represents the mass of gas flowing per unit time.
- Volume Flow Rate: This is the amount of gas passing through a point in a system per unit time, measured in cubic meters per second (m³/s). It represents the volume of gas flowing per unit time.
Conversion between Mass Flow Rate and Volume Flow Rate:
To convert between mass flow rate and volume flow rate for gases, one needs to consider the gas density. The density of a gas is defined as its mass per unit volume. By multiplying the volume flow rate by the gas density, one can obtain the mass flow rate.
- Mass Flow Rate (kg/s) = Volume Flow Rate (m³/s) × Gas Density (kg/m³)
Explanation of the Correct Answer:
The correct answer, option 'D' (kgf/s), represents the flow rate of gases in terms of force per unit time. The use of kilogram-force (kgf) in this context is due to the historical convention of expressing force in terms of the gravitational force exerted on a mass of one kilogram.
- 1 kgf is defined as the force exerted by gravity on a mass of 1 kilogram.
- The unit kgf/s represents the force per unit time, which is equivalent to the mass flow rate (kg/s) when considering the acceleration due to gravity.
Conclusion:
In summary, the unit for flow rate of gases is kgf/s. This unit represents the force per unit time and is equivalent to the mass flow rate when considering the acceleration due to gravity.
A steady incompressible 2D flow field is given by u = 2x2 + y2 and v = −4xy. The convective acceleration along x-direction at point (1, 2) is- a) 6 units
- b) 24 units
- c) − 8 units
- d) − 24 units
Correct answer is option 'C'. Can you explain this answer?
A steady incompressible 2D flow field is given by u = 2x2 + y2 and v = −4xy. The convective acceleration along x-direction at point (1, 2) is
a)
6 units
b)
24 units
c)
− 8 units
d)
− 24 units
|
|
Sanvi Kapoor answered |
U = 2x2 + y2, v = −4xy
ax = (2x2 + y2)(4x) + (−4xy)(2y) + 0 + 0
∴ at point (1, 2) ax
= (2 + 4)(4) − (8)(4) ax
= 24 − 32 ax
= −8 units
When fluid element moves from one position to another, what type of motion is it?- a)Linear Translation
- b)Linear Deformation
- c)Angular Deformation
- d)Rotation
Correct answer is option 'A'. Can you explain this answer?
When fluid element moves from one position to another, what type of motion is it?
a)
Linear Translation
b)
Linear Deformation
c)
Angular Deformation
d)
Rotation

|
Aarav Kulkarni answered |
Explanation: As per the definition, bodily movement of fluid element is translation.
A fluid flow field is given by
V=y2xi+z2x-(2xyz+yz)k
Calculate it’s acceleration at the point (2,4,4)- a)36i-27j+100k
- b)36i-27j-100k
- c)28i+27j+100k
- d)36ne of the mentioned
Correct answer is option 'D'. Can you explain this answer?
A fluid flow field is given by
V=y2xi+z2x-(2xyz+yz)k
Calculate it’s acceleration at the point (2,4,4)
V=y2xi+z2x-(2xyz+yz)k
Calculate it’s acceleration at the point (2,4,4)
a)
36i-27j+100k
b)
36i-27j-100k
c)
28i+27j+100k
d)
36ne of the mentioned

|
Manasa Sen answered |
Explanation: First we have to check whether it satisfies the continuity equation,
The continuity equation for incompressible is du/dx+dv/dy+dw/dz = 0.
(here d/dx, d/dy, d/z represent partial derivative)
The given equation doesn’t satisfy the continuity equation.
The continuity equation for incompressible is du/dx+dv/dy+dw/dz = 0.
(here d/dx, d/dy, d/z represent partial derivative)
The given equation doesn’t satisfy the continuity equation.
Determine the third velocity component such that continuity equation is satisfied if two components are u=x2+y2+z2, v=xy2 – yz2 + xy
- a)-3xz-2xyz+z2/3+f(y,z)
- b)-3xz+2xyz+z3/3+f(y,z)
- c)-3xz-2xyz+z3/3+f(x,z)
- d)-3xz-2xyz+z3/3+f(x,y)
Correct answer is option 'D'. Can you explain this answer?
Determine the third velocity component such that continuity equation is satisfied if two components are u=x2+y2+z2, v=xy2 – yz2 + xy
a)
-3xz-2xyz+z2/3+f(y,z)
b)
-3xz+2xyz+z3/3+f(y,z)
c)
-3xz-2xyz+z3/3+f(x,z)
d)
-3xz-2xyz+z3/3+f(x,y)

|
Anand Kumar answered |
Explanation: The continuity equation for incompressible is du/dx+dv/dy+dw/dz = 0.
Here du/dx=2x and v=2xy-z2
On solving by integrating, we get w = -3xz-2xyz+z3/3+f(x,y),
Here du/dx=2x and v=2xy-z2
On solving by integrating, we get w = -3xz-2xyz+z3/3+f(x,y),
When a uniform flow is flowing through a doublet, resultant flow obtained is- a)Flow past a Rankine oval of equal axes
- b)Flow past a circular cylinder
- c)All of the mentioned
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
When a uniform flow is flowing through a doublet, resultant flow obtained is
a)
Flow past a Rankine oval of equal axes
b)
Flow past a circular cylinder
c)
All of the mentioned
d)
None of the mentioned

|
Sahil Chawla answered |
Flow through a Doublet
When a uniform flow is flowing through a doublet, the resultant flow obtained is a combination of the effects of both the uniform flow and the doublet.
Resultant Flow
The resultant flow obtained is a combination of both the flow past a Rankine oval of equal axes and the flow past a circular cylinder.
Flow past a Rankine Oval
A Rankine oval is a theoretical shape used to represent the flow around a body in potential flow. When a uniform flow passes a doublet, it creates a flow pattern similar to that past a Rankine oval of equal axes.
Flow past a Circular Cylinder
In addition to the flow around a Rankine oval, the flow past a doublet also resembles the flow around a circular cylinder. The combination of these two flow patterns gives rise to the resultant flow obtained when a uniform flow passes through a doublet.
Conclusion
Therefore, the correct answer is option C - All of the mentioned, as the resultant flow obtained when a uniform flow is flowing through a doublet exhibits characteristics of both flow past a Rankine oval and flow past a circular cylinder.
When a uniform flow is flowing through a doublet, the resultant flow obtained is a combination of the effects of both the uniform flow and the doublet.
Resultant Flow
The resultant flow obtained is a combination of both the flow past a Rankine oval of equal axes and the flow past a circular cylinder.
Flow past a Rankine Oval
A Rankine oval is a theoretical shape used to represent the flow around a body in potential flow. When a uniform flow passes a doublet, it creates a flow pattern similar to that past a Rankine oval of equal axes.
Flow past a Circular Cylinder
In addition to the flow around a Rankine oval, the flow past a doublet also resembles the flow around a circular cylinder. The combination of these two flow patterns gives rise to the resultant flow obtained when a uniform flow passes through a doublet.
Conclusion
Therefore, the correct answer is option C - All of the mentioned, as the resultant flow obtained when a uniform flow is flowing through a doublet exhibits characteristics of both flow past a Rankine oval and flow past a circular cylinder.
Which of the following is not a case of ideal fluid flow?- a)Forced vortex Flow
- b)Uniform Flow
- c)Sink Flow
- d)Superimposed flow
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a case of ideal fluid flow?
a)
Forced vortex Flow
b)
Uniform Flow
c)
Sink Flow
d)
Superimposed flow

|
Sravya Rane answered |
Introduction:
Ideal fluid flow refers to the flow of a fluid that is assumed to have no viscosity or internal friction. In ideal fluid flow, the fluid particles move without any resistance, and the flow is governed by the principles of conservation of mass and energy. Several types of ideal fluid flow exist, but one of them is not a case of ideal fluid flow.
Forced Vortex Flow:
Forced vortex flow is a type of fluid flow in which the fluid particles move in circles or concentric paths around a central axis. This type of flow occurs when a fluid is forced to rotate within a confined space, such as in a vortex chamber. In forced vortex flow, the tangential velocity of the fluid particles increases as the distance from the central axis increases, while the radial velocity remains constant. This type of flow is a case of ideal fluid flow.
Uniform Flow:
Uniform flow refers to the type of fluid flow in which the velocity of the fluid remains constant at every point in the flow field. In uniform flow, the fluid particles move parallel to each other and have the same velocity magnitude. This type of flow is a case of ideal fluid flow.
Sink Flow:
Sink flow, also known as source flow, refers to the type of fluid flow in which the fluid particles converge towards a central point or sink. In sink flow, the fluid particles move radially inward towards the sink, and the velocity magnitude decreases as the distance from the sink decreases. This type of flow is a case of ideal fluid flow.
Superimposed Flow:
Superimposed flow refers to the type of fluid flow that occurs when two or more flows are combined or superimposed on each other. This can happen, for example, when two fluid streams with different velocities and directions are combined. Superimposed flow can result in complex flow patterns, but it is still a case of ideal fluid flow.
Conclusion:
Out of the given options, the case that is not a case of ideal fluid flow is the forced vortex flow (option A). Forced vortex flow involves a rotating fluid, which introduces rotational motion and non-uniform velocity profiles. In ideal fluid flow, the fluid particles do not experience any resistance or internal friction, and the flow is characterized by uniform velocity and no rotational motion.
Ideal fluid flow refers to the flow of a fluid that is assumed to have no viscosity or internal friction. In ideal fluid flow, the fluid particles move without any resistance, and the flow is governed by the principles of conservation of mass and energy. Several types of ideal fluid flow exist, but one of them is not a case of ideal fluid flow.
Forced Vortex Flow:
Forced vortex flow is a type of fluid flow in which the fluid particles move in circles or concentric paths around a central axis. This type of flow occurs when a fluid is forced to rotate within a confined space, such as in a vortex chamber. In forced vortex flow, the tangential velocity of the fluid particles increases as the distance from the central axis increases, while the radial velocity remains constant. This type of flow is a case of ideal fluid flow.
Uniform Flow:
Uniform flow refers to the type of fluid flow in which the velocity of the fluid remains constant at every point in the flow field. In uniform flow, the fluid particles move parallel to each other and have the same velocity magnitude. This type of flow is a case of ideal fluid flow.
Sink Flow:
Sink flow, also known as source flow, refers to the type of fluid flow in which the fluid particles converge towards a central point or sink. In sink flow, the fluid particles move radially inward towards the sink, and the velocity magnitude decreases as the distance from the sink decreases. This type of flow is a case of ideal fluid flow.
Superimposed Flow:
Superimposed flow refers to the type of fluid flow that occurs when two or more flows are combined or superimposed on each other. This can happen, for example, when two fluid streams with different velocities and directions are combined. Superimposed flow can result in complex flow patterns, but it is still a case of ideal fluid flow.
Conclusion:
Out of the given options, the case that is not a case of ideal fluid flow is the forced vortex flow (option A). Forced vortex flow involves a rotating fluid, which introduces rotational motion and non-uniform velocity profiles. In ideal fluid flow, the fluid particles do not experience any resistance or internal friction, and the flow is characterized by uniform velocity and no rotational motion.
What is the nature of streamlines of free vortex flow?- a)Concentric
- b)Non-concentric
- c)Linear
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
What is the nature of streamlines of free vortex flow?
a)
Concentric
b)
Non-concentric
c)
Linear
d)
None of the mentioned

|
Isha Bajaj answered |
Streamlines of free vortex flow
Definition:
Free vortex flow is a type of fluid flow where the fluid particles rotate about a central axis in a circular path without any radial motion. The streamlines in free vortex flow are the paths followed by fluid particles in the flow field.
Nature of streamlines:
The nature of streamlines in free vortex flow is concentric. This means that the streamlines are circular and concentric around a central axis. The circular streamlines indicate that the fluid particles are rotating about the central axis, forming a vortex.
Explanation:
In free vortex flow, the fluid motion is induced by the rotation of a solid body or due to an external force. The streamlines in this type of flow are determined by the balance between the centrifugal force and the pressure gradient.
When a fluid particle is in free vortex flow, it experiences a centrifugal force due to its rotation about the central axis. This centrifugal force causes the fluid particle to move away from the central axis. However, the pressure gradient in the flow field is directed towards the center, acting as a restoring force. This pressure gradient balances the centrifugal force, resulting in a circular path followed by the fluid particle.
As a result, the streamlines in free vortex flow are concentric circles around the central axis. Each streamline represents a different circular path followed by the fluid particles in the flow. The radius of the streamlines increases as we move away from the central axis, indicating an increase in the velocity of the fluid particles.
Conclusion:
In summary, the nature of streamlines in free vortex flow is concentric. The streamlines are circular and concentric around a central axis, representing the paths followed by the fluid particles in the flow field.
Definition:
Free vortex flow is a type of fluid flow where the fluid particles rotate about a central axis in a circular path without any radial motion. The streamlines in free vortex flow are the paths followed by fluid particles in the flow field.
Nature of streamlines:
The nature of streamlines in free vortex flow is concentric. This means that the streamlines are circular and concentric around a central axis. The circular streamlines indicate that the fluid particles are rotating about the central axis, forming a vortex.
Explanation:
In free vortex flow, the fluid motion is induced by the rotation of a solid body or due to an external force. The streamlines in this type of flow are determined by the balance between the centrifugal force and the pressure gradient.
When a fluid particle is in free vortex flow, it experiences a centrifugal force due to its rotation about the central axis. This centrifugal force causes the fluid particle to move away from the central axis. However, the pressure gradient in the flow field is directed towards the center, acting as a restoring force. This pressure gradient balances the centrifugal force, resulting in a circular path followed by the fluid particle.
As a result, the streamlines in free vortex flow are concentric circles around the central axis. Each streamline represents a different circular path followed by the fluid particles in the flow. The radius of the streamlines increases as we move away from the central axis, indicating an increase in the velocity of the fluid particles.
Conclusion:
In summary, the nature of streamlines in free vortex flow is concentric. The streamlines are circular and concentric around a central axis, representing the paths followed by the fluid particles in the flow field.
Consider fully developed axisymmetric Poiseuille flow in a round pipe of radius R with a pressure gradient (∂p/ ∂x) driving the flow as shown in figure (∂p/ ∂x is uniform and negative). The flow is steady, incompressible and axisymmetric about the x-axis. The velocity components are given byuz = 1 / 4μ ( ∂p / ∂x ) (r2 − R2 ); ur = 0; uθ = 0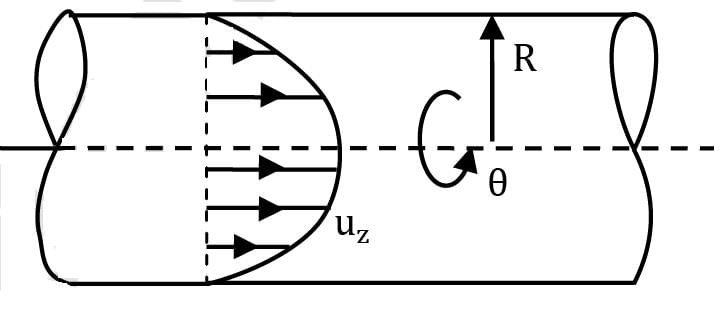
- a)Flow is irrotational
- b) Flow is rotational and vorticity component is 1 / 4μ (∂p / ∂x ) (2r) clockwise.
- c) Flow is rotational and vorticity component is 1 /4μ (∂p ∂/ x ) (2r) anti clockwise
- d) Flow is rotational and vorticity component is 1 / 2μ (∂p / ∂x ) (2r)
Correct answer is option 'C'. Can you explain this answer?
Consider fully developed axisymmetric Poiseuille flow in a round pipe of radius R with a pressure gradient (∂p/ ∂x) driving the flow as shown in figure (∂p/ ∂x is uniform and negative). The flow is steady, incompressible and axisymmetric about the x-axis. The velocity components are given by
uz = 1 / 4μ ( ∂p / ∂x ) (r2 − R2 ); ur = 0; uθ = 0

a)
Flow is irrotational
b)
Flow is rotational and vorticity component is 1 / 4μ (∂p / ∂x ) (2r) clockwise.
c)
Flow is rotational and vorticity component is 1 /4μ (∂p ∂/ x ) (2r) anti clockwise
d)
Flow is rotational and vorticity component is 1 / 2μ (∂p / ∂x ) (2r)
|
|
Sanvi Kapoor answered |

ince ∂p/ ∂x is also negative therefore, Ω will be positive. Hence according to convention of FM (+)ve sign indicates anticlockwise rotation.
Therefore the correct option is (C).
Three pipe flows named as 1,2 and 3 are observed. The Reynold’s number for the three are 100, 1000 and 10000. Which of the flows will be laminar?- a)only 1
- b)only 1 and 2
- c)1, 2 and 3
- d)only 3
Correct answer is option 'B'. Can you explain this answer?
Three pipe flows named as 1,2 and 3 are observed. The Reynold’s number for the three are 100, 1000 and 10000. Which of the flows will be laminar?
a)
only 1
b)
only 1 and 2
c)
1, 2 and 3
d)
only 3

|
Srestha Khanna answered |
Explanation: Flows can be characterized as laminar or turbulent on the basis of Reynold’s number Re = ρvd / μ, where ρ is the density, d is the pipe diameter and μ is the viscosity. For Re < 2000, the flow will be laminar and Re > 4000, the flow will be turbulent. Thus, flow 1 and 2 will be laminar.
In free vortex flow, the flow is linear in nature.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
In free vortex flow, the flow is linear in nature.
a)
True
b)
False

|
Raghavendra Goyal answered |
Explanation : In free vortex flow, the flow is circular in nature.
Verify whether the following functions are valid potential functions.
(i) ϕ = A(X2 − Y2)
(ii) ϕ = Acos x- a)Both are valid potential functions
- b)Both are not valid potential functions
- c)(i) Is not a valid function (ii) Is a valid potential function
- d)(i) Is a valid potential function (ii) Not a valid function
Correct answer is option 'D'. Can you explain this answer?
Verify whether the following functions are valid potential functions.
(i) ϕ = A(X2 − Y2)
(ii) ϕ = Acos x
(i) ϕ = A(X2 − Y2)
(ii) ϕ = Acos x
a)
Both are valid potential functions
b)
Both are not valid potential functions
c)
(i) Is not a valid function (ii) Is a valid potential function
d)
(i) Is a valid potential function (ii) Not a valid function
|
|
Lavanya Menon answered |
Properties of Potential functions:
1. If velocity potential (ϕ) exists, the flow should be irrotational.
2. If velocity potential (ϕ) satisfies the Laplace equation, it represents the possible steady incompressible irrotational flow.
Calculation:
Given:
(i) ϕ = A(X2 − Y2), (ii) ϕ = Acos x.
(i) ϕ = A(X2 − Y2),
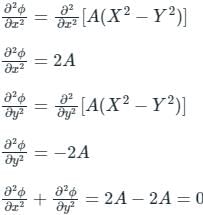
(ii) ϕ = Acos x
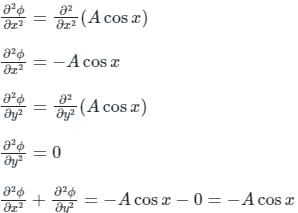
Thus (i) is a valid potential function as it satisfies the Laplace equation, whereas (ii) is not a valid potential function as it does not satisfy Laplace equation.
1. If velocity potential (ϕ) exists, the flow should be irrotational.
2. If velocity potential (ϕ) satisfies the Laplace equation, it represents the possible steady incompressible irrotational flow.
Calculation:
Given:
(i) ϕ = A(X2 − Y2), (ii) ϕ = Acos x.
(i) ϕ = A(X2 − Y2),
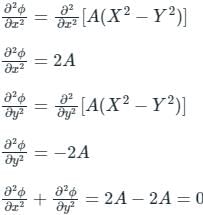
(ii) ϕ = Acos x
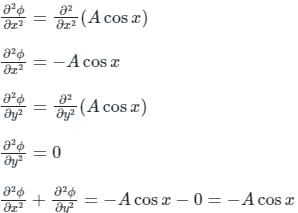
Thus (i) is a valid potential function as it satisfies the Laplace equation, whereas (ii) is not a valid potential function as it does not satisfy Laplace equation.
Which of the following is true?- a)Flow is laminar inside the boundary layer and turbulent outside
- b)Flow is turbulent inside the boundary layer and laminar outside
- c)Flow is laminar both inside and outside of the boundary layer
- d)Flow is turbulent both inside and outside of the boundary layer
Correct answer is option 'A'. Can you explain this answer?
Which of the following is true?
a)
Flow is laminar inside the boundary layer and turbulent outside
b)
Flow is turbulent inside the boundary layer and laminar outside
c)
Flow is laminar both inside and outside of the boundary layer
d)
Flow is turbulent both inside and outside of the boundary layer

|
Rajdeep Gupta answered |
Flow is laminar inside the boundary layer and turbulent outside
The statement that flow is laminar inside the boundary layer and turbulent outside is true. This is a characteristic of boundary layer flow, which is the thin layer of fluid that forms along a solid surface when it is exposed to a moving fluid. The boundary layer is divided into two regions: the laminar sublayer and the turbulent layer.
Explanation:
1. Boundary Layer Flow:
- When a fluid flows over a solid surface, such as air flowing over an aircraft wing or water flowing over a ship's hull, a boundary layer is formed.
- This boundary layer is a thin layer of fluid that adheres to the surface due to viscous effects.
- The boundary layer flow can be divided into two regions: the laminar sublayer and the turbulent layer.
2. Laminar Sublayer:
- The laminar sublayer is the region of flow closest to the solid surface.
- In this region, the flow is smooth and ordered, with the fluid particles moving in parallel layers.
- The fluid viscosity dominates in this region, and the flow is characterized by low velocity gradients and smooth streamlines.
- The flow in the laminar sublayer is called laminar flow.
3. Turbulent Layer:
- Outside the laminar sublayer, there is a region called the turbulent layer.
- In this region, the flow is characterized by chaotic motion, with the fluid particles moving in irregular patterns.
- The velocity gradients are higher, and the streamlines become more complex and unpredictable.
- The flow in the turbulent layer is called turbulent flow.
4. Transition from Laminar to Turbulent Flow:
- As the fluid flows over the surface, the laminar flow in the boundary layer may transition to turbulent flow.
- This transition occurs due to factors such as flow velocity, surface roughness, and pressure gradient.
- Once the flow becomes turbulent, it remains turbulent as it moves away from the surface.
5. Flow Characteristics:
- Inside the boundary layer, where the fluid is close to the surface, the flow is influenced by the smooth and ordered laminar sublayer.
- Therefore, the flow inside the boundary layer is laminar.
- Outside the boundary layer, where the flow is further away from the surface, the flow is influenced by the chaotic and irregular turbulent layer.
- Therefore, the flow outside the boundary layer is turbulent.
In conclusion, the statement that flow is laminar inside the boundary layer and turbulent outside is true. This is a characteristic of boundary layer flow, where the flow is smooth and ordered inside the laminar sublayer and chaotic and irregular outside the boundary layer.
The statement that flow is laminar inside the boundary layer and turbulent outside is true. This is a characteristic of boundary layer flow, which is the thin layer of fluid that forms along a solid surface when it is exposed to a moving fluid. The boundary layer is divided into two regions: the laminar sublayer and the turbulent layer.
Explanation:
1. Boundary Layer Flow:
- When a fluid flows over a solid surface, such as air flowing over an aircraft wing or water flowing over a ship's hull, a boundary layer is formed.
- This boundary layer is a thin layer of fluid that adheres to the surface due to viscous effects.
- The boundary layer flow can be divided into two regions: the laminar sublayer and the turbulent layer.
2. Laminar Sublayer:
- The laminar sublayer is the region of flow closest to the solid surface.
- In this region, the flow is smooth and ordered, with the fluid particles moving in parallel layers.
- The fluid viscosity dominates in this region, and the flow is characterized by low velocity gradients and smooth streamlines.
- The flow in the laminar sublayer is called laminar flow.
3. Turbulent Layer:
- Outside the laminar sublayer, there is a region called the turbulent layer.
- In this region, the flow is characterized by chaotic motion, with the fluid particles moving in irregular patterns.
- The velocity gradients are higher, and the streamlines become more complex and unpredictable.
- The flow in the turbulent layer is called turbulent flow.
4. Transition from Laminar to Turbulent Flow:
- As the fluid flows over the surface, the laminar flow in the boundary layer may transition to turbulent flow.
- This transition occurs due to factors such as flow velocity, surface roughness, and pressure gradient.
- Once the flow becomes turbulent, it remains turbulent as it moves away from the surface.
5. Flow Characteristics:
- Inside the boundary layer, where the fluid is close to the surface, the flow is influenced by the smooth and ordered laminar sublayer.
- Therefore, the flow inside the boundary layer is laminar.
- Outside the boundary layer, where the flow is further away from the surface, the flow is influenced by the chaotic and irregular turbulent layer.
- Therefore, the flow outside the boundary layer is turbulent.
In conclusion, the statement that flow is laminar inside the boundary layer and turbulent outside is true. This is a characteristic of boundary layer flow, where the flow is smooth and ordered inside the laminar sublayer and chaotic and irregular outside the boundary layer.
In laminar flow fluid particles flow along a streamline.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
In laminar flow fluid particles flow along a streamline.
a)
True
b)
False

|
Tanishq Nair answered |
Explanation: As per the definition of laminar flow, fluid particles flow in a streamlined manner.
In the equation for steam function due to source steam function is inversely proportional to magnitude at discharge- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
In the equation for steam function due to source steam function is inversely proportional to magnitude at discharge
a)
True
b)
False

|
Parth Patel answered |
Explanation: Steam function is directly proportional to magnitude of discharge.
Which of the following satisfies the Laplace Equation?- a)Stream function and Velocity Potential Function
- b)Only Velocity Potential function
- c)Only Stream function
- d)Neither Stream function nor Velocity Potential function
Correct answer is option 'B'. Can you explain this answer?
Which of the following satisfies the Laplace Equation?
a)
Stream function and Velocity Potential Function
b)
Only Velocity Potential function
c)
Only Stream function
d)
Neither Stream function nor Velocity Potential function

|
Tanishq Nair answered |
The Laplace equation is a partial differential equation that describes the behavior of many physical phenomena, such as heat flow, electrostatics, and fluid dynamics. In the context of fluid dynamics, the Laplace equation is used to describe the behavior of a fluid flow that is both steady and irrotational.
Velocity Potential Function:
A velocity potential function is a scalar field that describes the velocity of a fluid flow as a function of position. It satisfies the Laplace equation, which means that it describes a fluid flow that is both steady and irrotational.
Stream Function:
A stream function is a scalar field that describes the flow of a fluid in terms of its paths or streamlines. It also satisfies the Laplace equation, which means that it describes a fluid flow that is both steady and irrotational.
Answer:
Option 'B' Only Velocity Potential function satisfies the Laplace Equation. The reason is that the velocity potential function is a scalar field that describes the velocity of a fluid flow as a function of position. It satisfies the Laplace equation, which means that it describes a fluid flow that is both steady and irrotational. The stream function also satisfies the Laplace equation, but it describes the flow of a fluid in terms of its paths or streamlines, not its velocity. Therefore, the correct answer is option 'B'.
Velocity Potential Function:
A velocity potential function is a scalar field that describes the velocity of a fluid flow as a function of position. It satisfies the Laplace equation, which means that it describes a fluid flow that is both steady and irrotational.
Stream Function:
A stream function is a scalar field that describes the flow of a fluid in terms of its paths or streamlines. It also satisfies the Laplace equation, which means that it describes a fluid flow that is both steady and irrotational.
Answer:
Option 'B' Only Velocity Potential function satisfies the Laplace Equation. The reason is that the velocity potential function is a scalar field that describes the velocity of a fluid flow as a function of position. It satisfies the Laplace equation, which means that it describes a fluid flow that is both steady and irrotational. The stream function also satisfies the Laplace equation, but it describes the flow of a fluid in terms of its paths or streamlines, not its velocity. Therefore, the correct answer is option 'B'.
Find the acceleration of a fluid particle at the point r = 2a, θ = π/2 for a 2-D flow given byVr = −u (1 −a2 / r2) cos θVθ = u (1 + a2 / r2 ) sin θ- a) ar = 5u2 / 16a ; aθ = 0
- b) ar = 0 ; aθ = 5u2 / 16a
- c) ar = 0 ; aθ = −5u2 / 16a
- d) ar = −5u2 / 16a ; aθ = 0
Correct answer is option 'D'. Can you explain this answer?
Find the acceleration of a fluid particle at the point r = 2a, θ = π/2 for a 2-D flow given by
Vr = −u (1 −a2 / r2) cos θ
Vθ = u (1 + a2 / r2 ) sin θ
a)
ar = 5u2 / 16a ; aθ = 0
b)
ar = 0 ; aθ = 5u2 / 16a
c)
ar = 0 ; aθ = −5u2 / 16a
d)
ar = −5u2 / 16a ; aθ = 0
|
|
Sanya Agarwal answered |
Acceleration in radial direction is given by,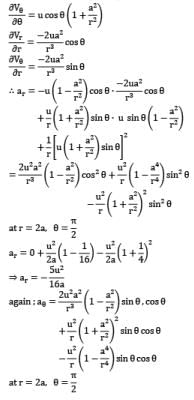
ar = Vr ∂Vr / ∂r + Vθ / r ∂Vr / ∂θ −Vθ2 /r
and acceleration in azimuthal direction is given by,
aθ = Vr ∂Vθ /∂r + Vθ / r ∂Vθ /∂θ + Vr Vθ /r
Now ∂Vr / ∂θ = u sin θ (1 − a 2 /r2)
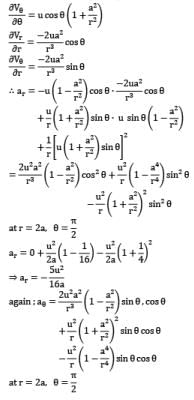
aθ = 0 + 0 − 0 ⇒ aθ = 0
∴ Option (D) is correct.
Potential lines for the source-sink pair will be eccentric non intersecting circles with their centers on the axis.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Potential lines for the source-sink pair will be eccentric non intersecting circles with their centers on the axis.
a)
True
b)
False

|
Prasad Desai answered |
Explanation: The potential line for the source sink pair will be eccentric non intersecting circles with their centers on the axis.
The flow of fluid along curvilinear or curved path is known as- a)Curvilinear Flow
- b)Circular Flow
- c)Sink Flow
- d)Vortex Flow
Correct answer is option 'D'. Can you explain this answer?
The flow of fluid along curvilinear or curved path is known as
a)
Curvilinear Flow
b)
Circular Flow
c)
Sink Flow
d)
Vortex Flow

|
Aarav Kulkarni answered |
Explanation: The flow of fluid along curvilinear or curved path is known as Vortex flow.
If the stream function for a 2D flow is given as ψ = 3xy, then the velocity at the point (2, 3) will be- a) 7.21 units
- b) 18 units
- c) 10.82 units
- d) 54 units
Correct answer is option 'C'. Can you explain this answer?
If the stream function for a 2D flow is given as ψ = 3xy, then the velocity at the point (2, 3) will be
a)
7.21 units
b)
18 units
c)
10.82 units
d)
54 units

|
Arshiya Roy answered |
To determine the velocity at a given point (2, 3) in a 2D flow, we can use the relationship between the stream function (ψ) and the velocity components (u, v) given by:
u = ∂ψ/∂y
v = -∂ψ/∂x
Given that the stream function ψ = 3xy, we can calculate the velocity components at the point (2, 3) as follows:
1. Calculating ∂ψ/∂y:
∂ψ/∂y = 3x
Substituting x = 2:
∂ψ/∂y = 3(2) = 6
2. Calculating ∂ψ/∂x:
∂ψ/∂x = -3y
Substituting y = 3:
∂ψ/∂x = -3(3) = -9
3. Calculating the velocity components:
u = ∂ψ/∂y = 6
v = -∂ψ/∂x = -(-9) = 9
Therefore, the velocity components at the point (2, 3) are u = 6 and v = 9.
To find the magnitude of the velocity, we can use the following formula:
Velocity magnitude = √(u^2 + v^2)
Substituting the values of u and v:
Velocity magnitude = √(6^2 + 9^2)
Velocity magnitude = √(36 + 81)
Velocity magnitude = √117
Velocity magnitude ≈ 10.82 units
So, the correct answer is option C) 10.82 units.
u = ∂ψ/∂y
v = -∂ψ/∂x
Given that the stream function ψ = 3xy, we can calculate the velocity components at the point (2, 3) as follows:
1. Calculating ∂ψ/∂y:
∂ψ/∂y = 3x
Substituting x = 2:
∂ψ/∂y = 3(2) = 6
2. Calculating ∂ψ/∂x:
∂ψ/∂x = -3y
Substituting y = 3:
∂ψ/∂x = -3(3) = -9
3. Calculating the velocity components:
u = ∂ψ/∂y = 6
v = -∂ψ/∂x = -(-9) = 9
Therefore, the velocity components at the point (2, 3) are u = 6 and v = 9.
To find the magnitude of the velocity, we can use the following formula:
Velocity magnitude = √(u^2 + v^2)
Substituting the values of u and v:
Velocity magnitude = √(6^2 + 9^2)
Velocity magnitude = √(36 + 81)
Velocity magnitude = √117
Velocity magnitude ≈ 10.82 units
So, the correct answer is option C) 10.82 units.
For compressible flow specific gravity remains same. - a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
For compressible flow specific gravity remains same.
a)
True
b)
False

|
Aarav Chauhan answered |
Explanation: For compressible flow, density changes and therefore specific gravity changes.
A stream function is given by (x2 − y2). The velocity potential function of the flow will be- a) 2xy + f(x)
- b) 2xy + constant
- c) 2(x2 − y2)
- d) 2xy + f(y)
Correct answer is option 'B'. Can you explain this answer?
A stream function is given by (x2 − y2). The velocity potential function of the flow will be
a)
2xy + f(x)
b)
2xy + constant
c)
2(x2 − y2)
d)
2xy + f(y)
|
|
Sanvi Kapoor answered |
Ψ = x2 − y 2
From definition of stream function (ψ)
∂ψ / ∂y = u and ∂ψ / ∂x = −v
hence u = −2y, v = −2x We also know that ∂ϕ /∂x = −u and ∂ϕ /∂y = −v
i. e ∂ϕ / ∂x = 2y and ∂ϕ / ∂y = 2x
Now dϕ = ∂ϕ / ∂x dx + ∂ϕ ∂y / dy
⟹ dϕ = 2ydx + 2xdy
ϕ = 2yx + 2xy + C
ϕ = 4(xy) + C or
ϕ = 2xy + K
where K is constant.
In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax2 + bxy and v = bxy + ay2. The condition for the flow field to be continuous is- a)independent of the constants (a; b) but dependent on the variables (x; y)
- b)independent of the variables (x; y) but dependent on the constants (a; b)
- c)independent of both the constants (a; b) and the variables (x; y)
- d)dependent on both the constants (a; b) and the variables (x; y)
Correct answer is option 'A'. Can you explain this answer?
In a two dimensional flow, the component of the velocity along the X-axis and the Y-axis are u = ax2 + bxy and v = bxy + ay2. The condition for the flow field to be continuous is
a)
independent of the constants (a; b) but dependent on the variables (x; y)
b)
independent of the variables (x; y) but dependent on the constants (a; b)
c)
independent of both the constants (a; b) and the variables (x; y)
d)
dependent on both the constants (a; b) and the variables (x; y)

|
Atharva Rane answered |
To determine the condition for the flow field to be continuous, we need to consider the continuity equation, which states that the rate of mass flow into a control volume must be equal to the rate of mass flow out of the control volume. In two-dimensional flow, this equation can be expressed as:
∂(ρu)/∂x + ∂(ρv)/∂y = 0
where ρ is the density of the fluid.
Now let's substitute the given expressions for u and v into the continuity equation and see if we can simplify it.
1. Substitute u = ax^2 + bxy and v = bxy + ay^2 into the continuity equation:
∂(ρ(ax^2 + bxy))/∂x + ∂(ρ(bxy + ay^2))/∂y = 0
2. Expand the derivatives:
2ax(ρa + ρbx) + 2by(ρb + ρay) = 0
3. Factor out the common terms:
2(ρa + ρbx)(ax + by) = 0
4. Equate each factor to zero:
ρa + ρbx = 0 (1)
ax + by = 0 (2)
Now let's analyze each factor separately.
Condition for (ρa + ρbx) = 0:
The factor ρa + ρbx represents a linear combination of constants (a and b) and variables (x and y). For this factor to be equal to zero, it means that the coefficients of the constants and variables must sum up to zero. Therefore, this condition is independent of the constants (a and b) but dependent on the variables (x and y).
Condition for (ax + by) = 0:
The factor ax + by represents a linear combination of variables (x and y) only. For this factor to be equal to zero, it means that the coefficients of x and y must sum up to zero. Therefore, this condition is independent of the constants (a and b) but dependent on the variables (x and y).
Conclusion:
Since both factors in the continuity equation have conditions that are independent of the constants (a and b) but dependent on the variables (x and y), the condition for the flow field to be continuous is independent of the constants (a and b) but dependent on the variables (x and y). Therefore, the correct answer is option 'A'.
∂(ρu)/∂x + ∂(ρv)/∂y = 0
where ρ is the density of the fluid.
Now let's substitute the given expressions for u and v into the continuity equation and see if we can simplify it.
1. Substitute u = ax^2 + bxy and v = bxy + ay^2 into the continuity equation:
∂(ρ(ax^2 + bxy))/∂x + ∂(ρ(bxy + ay^2))/∂y = 0
2. Expand the derivatives:
2ax(ρa + ρbx) + 2by(ρb + ρay) = 0
3. Factor out the common terms:
2(ρa + ρbx)(ax + by) = 0
4. Equate each factor to zero:
ρa + ρbx = 0 (1)
ax + by = 0 (2)
Now let's analyze each factor separately.
Condition for (ρa + ρbx) = 0:
The factor ρa + ρbx represents a linear combination of constants (a and b) and variables (x and y). For this factor to be equal to zero, it means that the coefficients of the constants and variables must sum up to zero. Therefore, this condition is independent of the constants (a and b) but dependent on the variables (x and y).
Condition for (ax + by) = 0:
The factor ax + by represents a linear combination of variables (x and y) only. For this factor to be equal to zero, it means that the coefficients of x and y must sum up to zero. Therefore, this condition is independent of the constants (a and b) but dependent on the variables (x and y).
Conclusion:
Since both factors in the continuity equation have conditions that are independent of the constants (a and b) but dependent on the variables (x and y), the condition for the flow field to be continuous is independent of the constants (a and b) but dependent on the variables (x and y). Therefore, the correct answer is option 'A'.
Chapter doubts & questions for Fluid Kinematics - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Fluid Kinematics - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
6 Months Preparation for GATE Civil Engg
488 videos|1261 docs|878 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup










