All Exams >
Civil Engineering (CE) >
6 Months Preparation for GATE Civil Engg >
All Questions
All questions of Bending Stresses in Beams for Civil Engineering (CE) Exam
For a beam of uniform strength, if its depth is kept constant, then its width will vary in proportion to- a)bending moment {M)
- b)√M
- c)M2
- d)M-1
Correct answer is option 'A'. Can you explain this answer?
For a beam of uniform strength, if its depth is kept constant, then its width will vary in proportion to
a)
bending moment {M)
b)
√M
c)
M2
d)
M-1
|
|
Sarita Yadav answered |
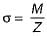
for beam of uniform strength, σ = constant at any section
so, M α Z
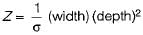
∴ M α width
At the neutral axis of simply beam, there is- a)maximum tensile stress
- b)maximum compressive stress
- c)zero bending stress
- d)stress developed which depends upon type of loading
Correct answer is option 'C'. Can you explain this answer?
At the neutral axis of simply beam, there is
a)
maximum tensile stress
b)
maximum compressive stress
c)
zero bending stress
d)
stress developed which depends upon type of loading
|
|
Aman Ghosh answered |
Bending stress,
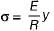
where y is the distance of any fibre from the neutral axis.
For the neutral axis, y = 0, ∴ σ = 0
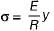
where y is the distance of any fibre from the neutral axis.
For the neutral axis, y = 0, ∴ σ = 0
Beams of uniform strength so vary in section that the- a)bending moment remains constant
- b)deflection remains constant
- c)unit stress remains constant
- d)all of the above remains constant
Correct answer is option 'C'. Can you explain this answer?
Beams of uniform strength so vary in section that the
a)
bending moment remains constant
b)
deflection remains constant
c)
unit stress remains constant
d)
all of the above remains constant

|
Prerna Kaur answered |
Unit stress means stress at any section.
A cantilever beam of rectangular cross-section is 1 m deep and 0.6 m thick. If the beam were to be 0.6 m deep and 1 m thick then the beam would - a)be weakened 0.5 times
- b)be weakened 0.6 times
- c)be strengthened 0.6 times
- d)have the same strength as the original beam because the cross-sectional area remains the same
Correct answer is option 'C'. Can you explain this answer?
A cantilever beam of rectangular cross-section is 1 m deep and 0.6 m thick. If the beam were to be 0.6 m deep and 1 m thick then the beam would
a)
be weakened 0.5 times
b)
be weakened 0.6 times
c)
be strengthened 0.6 times
d)
have the same strength as the original beam because the cross-sectional area remains the same

|
Tanishq Rane answered |
Explanation:
To understand why the beam would be strengthened 0.6 times, we need to consider the moment of inertia of the beam.
The moment of inertia (I) of a rectangular cross-section beam is given by the equation:
I = (b * h^3) / 12
Where b is the breadth or thickness of the beam, and h is the depth of the beam.
Original Beam:
In the original beam, the breadth (b) is 0.6 m and the depth (h) is 1 m. Therefore, the moment of inertia (I1) can be calculated as:
I1 = (0.6 * 1^3) / 12 = 0.05 m^4
Modified Beam:
In the modified beam, the breadth (b) is 1 m and the depth (h) is 0.6 m. Therefore, the moment of inertia (I2) can be calculated as:
I2 = (1 * 0.6^3) / 12 = 0.036 m^4
Comparison:
To compare the strengths of the two beams, we can compare their moments of inertia. A higher moment of inertia indicates a stronger beam.
The ratio of the moment of inertia of the modified beam (I2) to the moment of inertia of the original beam (I1) can be calculated as:
Ratio = I2 / I1 = 0.036 / 0.05 = 0.72
Therefore, the modified beam is 0.72 times as strong as the original beam.
Conclusion:
Since the modified beam has a higher moment of inertia, it is stronger than the original beam. Thus, the correct answer is option 'C': the beam would be strengthened 0.6 times.
To understand why the beam would be strengthened 0.6 times, we need to consider the moment of inertia of the beam.
The moment of inertia (I) of a rectangular cross-section beam is given by the equation:
I = (b * h^3) / 12
Where b is the breadth or thickness of the beam, and h is the depth of the beam.
Original Beam:
In the original beam, the breadth (b) is 0.6 m and the depth (h) is 1 m. Therefore, the moment of inertia (I1) can be calculated as:
I1 = (0.6 * 1^3) / 12 = 0.05 m^4
Modified Beam:
In the modified beam, the breadth (b) is 1 m and the depth (h) is 0.6 m. Therefore, the moment of inertia (I2) can be calculated as:
I2 = (1 * 0.6^3) / 12 = 0.036 m^4
Comparison:
To compare the strengths of the two beams, we can compare their moments of inertia. A higher moment of inertia indicates a stronger beam.
The ratio of the moment of inertia of the modified beam (I2) to the moment of inertia of the original beam (I1) can be calculated as:
Ratio = I2 / I1 = 0.036 / 0.05 = 0.72
Therefore, the modified beam is 0.72 times as strong as the original beam.
Conclusion:
Since the modified beam has a higher moment of inertia, it is stronger than the original beam. Thus, the correct answer is option 'C': the beam would be strengthened 0.6 times.
A rod of length L and diameter D is subjected to a tensile load P. Which of the following is sufficient to calculate the resulting change in diameter?
- a)Young’s modulus
- b)Shear modulus
- c)Poisson’s ratio
- d)Both Young’s modulus and shear modulus
Correct answer is option 'D'. Can you explain this answer?
A rod of length L and diameter D is subjected to a tensile load P. Which of the following is sufficient to calculate the resulting change in diameter?
a)
Young’s modulus
b)
Shear modulus
c)
Poisson’s ratio
d)
Both Young’s modulus and shear modulus

|
Shalini Deshpande answered |
's modulus and Poisson's ratio of the material
b)Young's modulus and shear modulus of the material
c)Poisson's ratio and shear modulus of the material
d)Only the diameter of the rod before and after the load is applied
a) Young's modulus and Poisson's ratio of the material are sufficient to calculate the resulting change in diameter. Poisson's ratio describes the ratio of lateral strain to axial strain, and together with Young's modulus, which describes the stiffness of the material, can be used to calculate the amount of deformation the rod undergoes under tension. The change in diameter can then be calculated using the relationship between the axial and lateral strains.
b) Shear modulus is not necessary for calculating the change in diameter under tensile load.
c) Poisson's ratio and shear modulus can also be used to calculate the change in diameter, but Young's modulus is still needed to fully describe the material's response to tension.
d) Only knowing the diameter before and after the load is applied is not sufficient to calculate the resulting change in diameter, as it does not take into account the material properties or the magnitude of the load.
b)Young's modulus and shear modulus of the material
c)Poisson's ratio and shear modulus of the material
d)Only the diameter of the rod before and after the load is applied
a) Young's modulus and Poisson's ratio of the material are sufficient to calculate the resulting change in diameter. Poisson's ratio describes the ratio of lateral strain to axial strain, and together with Young's modulus, which describes the stiffness of the material, can be used to calculate the amount of deformation the rod undergoes under tension. The change in diameter can then be calculated using the relationship between the axial and lateral strains.
b) Shear modulus is not necessary for calculating the change in diameter under tensile load.
c) Poisson's ratio and shear modulus can also be used to calculate the change in diameter, but Young's modulus is still needed to fully describe the material's response to tension.
d) Only knowing the diameter before and after the load is applied is not sufficient to calculate the resulting change in diameter, as it does not take into account the material properties or the magnitude of the load.
The product El is known as- a)section modulus
- b)modulus of rupture
- c)flexural rigidity
- d)polar modulus
Correct answer is option 'C'. Can you explain this answer?
The product El is known as
a)
section modulus
b)
modulus of rupture
c)
flexural rigidity
d)
polar modulus

|
Bhargavi Sarkar answered |
Understanding El in Mechanical Engineering
The term "El" is commonly associated with the concept of flexural rigidity in mechanical engineering. Flexural rigidity is a critical property that describes a material's ability to resist bending when subjected to external loads.
What is Flexural Rigidity?
- Flexural rigidity (El) is defined as the product of the material's modulus of elasticity (E) and the moment of inertia (I) of the beam's cross-section.
- It quantifies how much a beam will deflect under a given load, making it essential for structural analysis and design.
Importance of Flexural Rigidity (El)
- Structural Integrity: Ensures that beams and structural elements maintain their shape and strength under loading conditions.
- Design Optimization: Engineers use El to optimize material selection and cross-section shapes for efficiency and performance.
- Deflection Control: A higher flexural rigidity indicates lesser deflection, which is crucial in applications where precision is vital.
Comparison with Other Options
- Section Modulus: This measures the strength of a beam's cross-section but does not directly incorporate the material's elasticity.
- Modulus of Rupture: Refers to the maximum stress a material can withstand before failure, not specifically related to bending resistance.
- Polar Modulus: Used for torsional strength rather than flexural strength.
Conclusion
In summary, El represents flexural rigidity, which is fundamental in assessing how structural elements behave under bending loads. Understanding this concept is vital for engineers to ensure safety, reliability, and economic efficiency in their designs.
The term "El" is commonly associated with the concept of flexural rigidity in mechanical engineering. Flexural rigidity is a critical property that describes a material's ability to resist bending when subjected to external loads.
What is Flexural Rigidity?
- Flexural rigidity (El) is defined as the product of the material's modulus of elasticity (E) and the moment of inertia (I) of the beam's cross-section.
- It quantifies how much a beam will deflect under a given load, making it essential for structural analysis and design.
Importance of Flexural Rigidity (El)
- Structural Integrity: Ensures that beams and structural elements maintain their shape and strength under loading conditions.
- Design Optimization: Engineers use El to optimize material selection and cross-section shapes for efficiency and performance.
- Deflection Control: A higher flexural rigidity indicates lesser deflection, which is crucial in applications where precision is vital.
Comparison with Other Options
- Section Modulus: This measures the strength of a beam's cross-section but does not directly incorporate the material's elasticity.
- Modulus of Rupture: Refers to the maximum stress a material can withstand before failure, not specifically related to bending resistance.
- Polar Modulus: Used for torsional strength rather than flexural strength.
Conclusion
In summary, El represents flexural rigidity, which is fundamental in assessing how structural elements behave under bending loads. Understanding this concept is vital for engineers to ensure safety, reliability, and economic efficiency in their designs.
The assumption “the plane section before bending remains plane after bending” made in the theory of bending implies:- a)strain is uniform along the length of beam
- b)bending stress is same at every section of the beam
- c)bending stress is proportional to strain at all sections
- d)strain is not proportional to distance from the neutral axis
Correct answer is option 'A'. Can you explain this answer?
The assumption “the plane section before bending remains plane after bending” made in the theory of bending implies:
a)
strain is uniform along the length of beam
b)
bending stress is same at every section of the beam
c)
bending stress is proportional to strain at all sections
d)
strain is not proportional to distance from the neutral axis
|
|
Isha Nambiar answered |
Explanation:
Assumption in the theory of bending:
- The assumption that "the plane section before bending remains plane after bending" implies that the strain is uniform along the length of the beam.
Explanation:
- When a beam is subjected to bending, the top fibers of the beam are in compression while the bottom fibers are in tension.
- Due to this, the beam undergoes deformation, resulting in strain.
- The assumption that the plane section remains plane after bending means that the strain is the same throughout the length of the beam.
Implications:
- This assumption leads to the conclusion that the strain is uniform along the length of the beam.
- It does not necessarily imply that bending stress is the same at every section of the beam or that bending stress is proportional to strain at all sections.
- The assumption simply states that the deformation of the beam is consistent and uniform along its length.
Therefore, the correct implication of the assumption "the plane section before bending remains plane after bending" is that strain is uniform along the length of the beam.
Assumption in the theory of bending:
- The assumption that "the plane section before bending remains plane after bending" implies that the strain is uniform along the length of the beam.
Explanation:
- When a beam is subjected to bending, the top fibers of the beam are in compression while the bottom fibers are in tension.
- Due to this, the beam undergoes deformation, resulting in strain.
- The assumption that the plane section remains plane after bending means that the strain is the same throughout the length of the beam.
Implications:
- This assumption leads to the conclusion that the strain is uniform along the length of the beam.
- It does not necessarily imply that bending stress is the same at every section of the beam or that bending stress is proportional to strain at all sections.
- The assumption simply states that the deformation of the beam is consistent and uniform along its length.
Therefore, the correct implication of the assumption "the plane section before bending remains plane after bending" is that strain is uniform along the length of the beam.
A beam is said to be of uniform strength, if- a)bending moment is same throughout the beam
- b)shear stress is same throughout the beam
- c)deflection is same throughout the beam
- d)bending stress is same at every section along its longitudinal axis
Correct answer is option 'D'. Can you explain this answer?
A beam is said to be of uniform strength, if
a)
bending moment is same throughout the beam
b)
shear stress is same throughout the beam
c)
deflection is same throughout the beam
d)
bending stress is same at every section along its longitudinal axis
|
|
Stuti Bajaj answered |
Uniform Strength in a Beam
In mechanical engineering, the concept of uniform strength is essential when designing beams. A beam is a structural component that is subjected to various forces such as bending moments, shear stresses, and deflections. Uniform strength refers to a beam's ability to distribute stress and strain evenly along its longitudinal axis. It ensures that the beam remains structurally stable and can withstand the applied loads without failure or excessive deformation.
Bending Moment and Uniform Strength
The bending moment is a measure of the internal forces that cause a beam to bend. It is the product of the applied load and the distance from the load to a particular point on the beam. In a beam of uniform strength, the bending moment is the same at every section along its longitudinal axis. This means that the internal forces causing bending are evenly distributed throughout the beam. If the bending moment were to vary significantly along the beam, certain sections would be subjected to higher stresses, which could lead to failure.
Shear Stress and Uniform Strength
Shear stress refers to the force per unit area that acts parallel to the cross-section of a beam. In a beam of uniform strength, the shear stress is the same at every section along its longitudinal axis. This ensures that the beam's resistance to shear forces is consistent throughout its length. If the shear stress were to vary along the beam, certain sections would be more susceptible to shear failure, compromising the overall strength of the beam.
Deflection and Uniform Strength
Deflection is the displacement of a beam under the applied loads. In a beam of uniform strength, the deflection is the same at every section along its longitudinal axis. This means that the beam experiences uniform deformation, ensuring that it remains stable and maintains its structural integrity. If the deflection were to vary significantly along the beam, certain sections would experience excessive deformation, which could affect the overall performance of the beam.
Bending Stress and Uniform Strength
Bending stress is a measure of the internal forces that cause a beam to bend. It is calculated by dividing the bending moment by the section modulus of the beam. In a beam of uniform strength, the bending stress is the same at every section along its longitudinal axis. This means that the beam's resistance to bending is consistent throughout its length. If the bending stress were to vary significantly along the beam, certain sections would be subjected to higher stresses, increasing the risk of failure.
Conclusion
In conclusion, a beam is said to be of uniform strength when the bending moment, shear stress, deflection, and bending stress are all the same at every section along its longitudinal axis. This ensures that the beam can effectively distribute the applied loads and maintain structural stability. By designing beams with uniform strength, engineers can optimize their performance and ensure their safety in various applications.
In mechanical engineering, the concept of uniform strength is essential when designing beams. A beam is a structural component that is subjected to various forces such as bending moments, shear stresses, and deflections. Uniform strength refers to a beam's ability to distribute stress and strain evenly along its longitudinal axis. It ensures that the beam remains structurally stable and can withstand the applied loads without failure or excessive deformation.
Bending Moment and Uniform Strength
The bending moment is a measure of the internal forces that cause a beam to bend. It is the product of the applied load and the distance from the load to a particular point on the beam. In a beam of uniform strength, the bending moment is the same at every section along its longitudinal axis. This means that the internal forces causing bending are evenly distributed throughout the beam. If the bending moment were to vary significantly along the beam, certain sections would be subjected to higher stresses, which could lead to failure.
Shear Stress and Uniform Strength
Shear stress refers to the force per unit area that acts parallel to the cross-section of a beam. In a beam of uniform strength, the shear stress is the same at every section along its longitudinal axis. This ensures that the beam's resistance to shear forces is consistent throughout its length. If the shear stress were to vary along the beam, certain sections would be more susceptible to shear failure, compromising the overall strength of the beam.
Deflection and Uniform Strength
Deflection is the displacement of a beam under the applied loads. In a beam of uniform strength, the deflection is the same at every section along its longitudinal axis. This means that the beam experiences uniform deformation, ensuring that it remains stable and maintains its structural integrity. If the deflection were to vary significantly along the beam, certain sections would experience excessive deformation, which could affect the overall performance of the beam.
Bending Stress and Uniform Strength
Bending stress is a measure of the internal forces that cause a beam to bend. It is calculated by dividing the bending moment by the section modulus of the beam. In a beam of uniform strength, the bending stress is the same at every section along its longitudinal axis. This means that the beam's resistance to bending is consistent throughout its length. If the bending stress were to vary significantly along the beam, certain sections would be subjected to higher stresses, increasing the risk of failure.
Conclusion
In conclusion, a beam is said to be of uniform strength when the bending moment, shear stress, deflection, and bending stress are all the same at every section along its longitudinal axis. This ensures that the beam can effectively distribute the applied loads and maintain structural stability. By designing beams with uniform strength, engineers can optimize their performance and ensure their safety in various applications.
When a rectangular beam is loaded longitudinal, shear develops on- a)top fibre
- b)middle fibre
- c)bottom fibre
- d)every horizontal plane
Correct answer is option 'D'. Can you explain this answer?
When a rectangular beam is loaded longitudinal, shear develops on
a)
top fibre
b)
middle fibre
c)
bottom fibre
d)
every horizontal plane
|
|
Dishani Desai answered |
When a rectangular beam is loaded longitudinally, shear develops on every horizontal plane. To understand why this is the case, let's break down the concept step by step.
1. Understanding Shear Stress:
Shear stress is a force that acts parallel to a surface, causing one layer of the material to slide past another. In the case of a rectangular beam, shear stress occurs in the horizontal direction.
2. Shear Distribution:
When a beam is loaded longitudinally, the applied load creates bending moments, resulting in shear forces being distributed throughout the beam. These shear forces act on every horizontal plane within the beam.
3. Analysis of Fibers:
To understand where shear develops, let's consider the different fibers within the beam:
a) Top Fiber: The top fiber of the beam experiences compressive stress due to the bending moment. However, it also experiences shear stress because it is subjected to the shear forces acting on the horizontal planes.
b) Middle Fiber: The middle fiber of the beam experiences neither compressive nor tensile stress due to the bending moment. However, it still experiences shear stress because it is also subjected to the shear forces acting on the horizontal planes.
c) Bottom Fiber: The bottom fiber of the beam experiences tensile stress due to the bending moment. Similar to the top and middle fibers, it also experiences shear stress because it is subjected to the shear forces acting on the horizontal planes.
4. Shear on Every Horizontal Plane:
Since shear stress is distributed throughout the beam, it affects all the fibers on every horizontal plane. This means that shear develops on the top fiber, middle fiber, and bottom fiber, as well as all the fibers in between.
5. Visualizing Shear Distribution:
To visualize the distribution of shear stress, imagine cutting the rectangular beam into multiple horizontal slices. Each slice represents a horizontal plane within the beam. On each slice, shear forces act, causing shear stress to develop on every fiber present.
In conclusion, when a rectangular beam is loaded longitudinally, shear develops on every horizontal plane, affecting all the fibers within the beam. This understanding is crucial for designing and analyzing the structural integrity of beams in mechanical engineering.
1. Understanding Shear Stress:
Shear stress is a force that acts parallel to a surface, causing one layer of the material to slide past another. In the case of a rectangular beam, shear stress occurs in the horizontal direction.
2. Shear Distribution:
When a beam is loaded longitudinally, the applied load creates bending moments, resulting in shear forces being distributed throughout the beam. These shear forces act on every horizontal plane within the beam.
3. Analysis of Fibers:
To understand where shear develops, let's consider the different fibers within the beam:
a) Top Fiber: The top fiber of the beam experiences compressive stress due to the bending moment. However, it also experiences shear stress because it is subjected to the shear forces acting on the horizontal planes.
b) Middle Fiber: The middle fiber of the beam experiences neither compressive nor tensile stress due to the bending moment. However, it still experiences shear stress because it is also subjected to the shear forces acting on the horizontal planes.
c) Bottom Fiber: The bottom fiber of the beam experiences tensile stress due to the bending moment. Similar to the top and middle fibers, it also experiences shear stress because it is subjected to the shear forces acting on the horizontal planes.
4. Shear on Every Horizontal Plane:
Since shear stress is distributed throughout the beam, it affects all the fibers on every horizontal plane. This means that shear develops on the top fiber, middle fiber, and bottom fiber, as well as all the fibers in between.
5. Visualizing Shear Distribution:
To visualize the distribution of shear stress, imagine cutting the rectangular beam into multiple horizontal slices. Each slice represents a horizontal plane within the beam. On each slice, shear forces act, causing shear stress to develop on every fiber present.
In conclusion, when a rectangular beam is loaded longitudinally, shear develops on every horizontal plane, affecting all the fibers within the beam. This understanding is crucial for designing and analyzing the structural integrity of beams in mechanical engineering.
Chapter doubts & questions for Bending Stresses in Beams - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Bending Stresses in Beams - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
6 Months Preparation for GATE Civil Engg
488 videos|1261 docs|878 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup


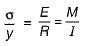 (Bending formula)
(Bending formula)








