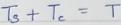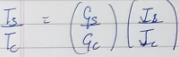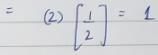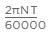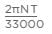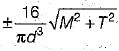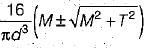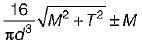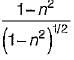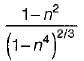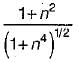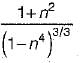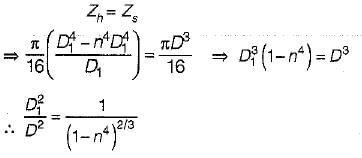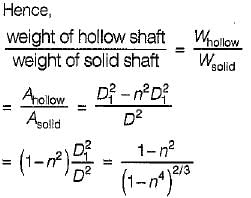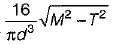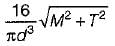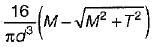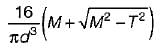All Exams >
Civil Engineering (CE) >
6 Months Preparation for GATE Civil Engg >
All Questions
All questions of Torsion of Shafts for Civil Engineering (CE) Exam
The outside diameter of a hollow shaft is twice its inside diameter. The ratio of its torque carrying capacity to that a solid shaft of the same material and the same outside diameter is- a)15/16
- b)3/4
- c)1/2
- d)1/16
Correct answer is option 'A'. Can you explain this answer?
The outside diameter of a hollow shaft is twice its inside diameter. The ratio of its torque carrying capacity to that a solid shaft of the same material and the same outside diameter is
a)
15/16
b)
3/4
c)
1/2
d)
1/16
|
|
Sanvi Kapoor answered |
The torque carrying capacity Tis given by

Let outside diameter of hollow and solid shaft = 2d
∴ Inside diameter of hollow shaft = d
∴ Inside diameter of hollow shaft = d
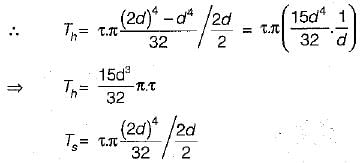
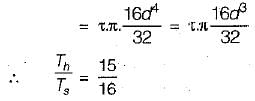
A shaft of diameter 'd' and length L is subjected to twisting moment T, shear angle developed in shaft is 0.001 rad. Now the length of the shaft is doubled, but the diameter and torque remain the same what will be the shear angle?- a)0.0005 rad
- b)0.001 rad
- c)0.002 rad
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A shaft of diameter 'd' and length L is subjected to twisting moment T, shear angle developed in shaft is 0.001 rad. Now the length of the shaft is doubled, but the diameter and torque remain the same what will be the shear angle?
a)
0.0005 rad
b)
0.001 rad
c)
0.002 rad
d)
None of these

|
Aarav Kulkarni answered |

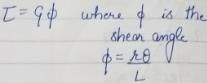
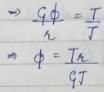

A close-coiled helical spring has 100 mm mean diameter and is made of 20 turns of 10 mm diameter steel wire. The spring carries an axial load of 100 N. Modulus of rigidity is 84 GPa. The shearing stress developed in the spring in N/mm2 is- a)120/π
- b)160/π
- c)100/π
- d)80/π
Correct answer is option 'D'. Can you explain this answer?
A close-coiled helical spring has 100 mm mean diameter and is made of 20 turns of 10 mm diameter steel wire. The spring carries an axial load of 100 N. Modulus of rigidity is 84 GPa. The shearing stress developed in the spring in N/mm2 is
a)
120/π
b)
160/π
c)
100/π
d)
80/π

|
Aditya Jain answered |
Closed coiled helical spring subjected to axial load (W) means that every section is subjected to torsion of WR where R is the radius of spring. From torsion formula,

d= diameter of wire
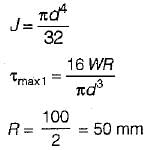
d = 10mm
W = 100 N
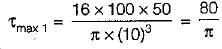
Shear stress due to load,
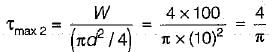

d= diameter of wire
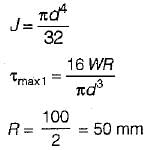
d = 10mm
W = 100 N
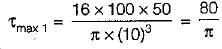
Shear stress due to load,
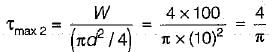
A spring with 25, active Coils cannot be accommodated within a given space. Hence 5 coils of the spring are cut. What is the stiffness of the new spring.- a)Same as the original spring
- b)1.25 times the original spring
- c)0.8 times the original spring
- d)0.5 times the. original spring
Correct answer is option 'B'. Can you explain this answer?
A spring with 25, active Coils cannot be accommodated within a given space. Hence 5 coils of the spring are cut. What is the stiffness of the new spring.
a)
Same as the original spring
b)
1.25 times the original spring
c)
0.8 times the original spring
d)
0.5 times the. original spring

|
Parth Patel answered |
As we know, k ∝ 1/n
∴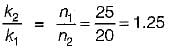
⇒ k2 = 1.25 k1
∴
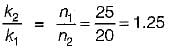
⇒ k2 = 1.25 k1
A hollow shaft of inner radius 30 mm and outer radius 50 mm is subjected to a twisting moment. If the shear stress developed at inner radius of shaft is 60 N/mm2. What is the maximum shear stress in shaft?- a)60 N/mm2
- b)75 N/mm2
- c)100 N/mm2
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A hollow shaft of inner radius 30 mm and outer radius 50 mm is subjected to a twisting moment. If the shear stress developed at inner radius of shaft is 60 N/mm2. What is the maximum shear stress in shaft?
a)
60 N/mm2
b)
75 N/mm2
c)
100 N/mm2
d)
None of these

|
Srestha Datta answered |
As we know, torsional shear stress varies linearly
∴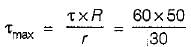
= 100N/mm2
∴
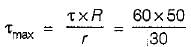
= 100N/mm2
If two shafts of the same length, one of which is hollow, transmit equal torque and have equal maximum stress, then they should have equal- a)Polar moment of inertia
- b)Polar modulus of section
- c)Diameter
- d)Angie of twist
Correct answer is option 'B'. Can you explain this answer?
If two shafts of the same length, one of which is hollow, transmit equal torque and have equal maximum stress, then they should have equal
a)
Polar moment of inertia
b)
Polar modulus of section
c)
Diameter
d)
Angie of twist

|
Anmol Roy answered |
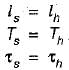
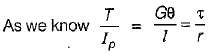
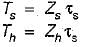
As Ts = Th,
∴ Zs = Zh
A solid shaft of diameter D carries a twisting moment that develops maximum shear stress τ. if the shaft is replaced by a hollow one of outside diameter ‘D’ and inside diameter D/2, then the maximum shear stress will be- a)1.067 τ
- b)1.143 τ
- c)1.330 τ
- d)2 τ
Correct answer is option 'A'. Can you explain this answer?
A solid shaft of diameter D carries a twisting moment that develops maximum shear stress τ. if the shaft is replaced by a hollow one of outside diameter ‘D’ and inside diameter D/2, then the maximum shear stress will be
a)
1.067 τ
b)
1.143 τ
c)
1.330 τ
d)
2 τ

|
Arnab Choudhury answered |
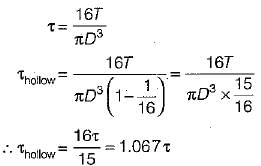
A carriage spring of span 'l’ consists of n plates each of thickness ‘t' and width b. If the spring carries a load w and modulus of elasticity of the spring is E, then the central deflection of the spring is- a)3wl3/8Enbt3
- b)3wl/Enbl3
- c)wl/4Enbt3
- d)wl2/8Enbt3
Correct answer is option 'A'. Can you explain this answer?
A carriage spring of span 'l’ consists of n plates each of thickness ‘t' and width b. If the spring carries a load w and modulus of elasticity of the spring is E, then the central deflection of the spring is
a)
3wl3/8Enbt3
b)
3wl/Enbl3
c)
wl/4Enbt3
d)
wl2/8Enbt3
|
|
Aditya Deshmukh answered |
The equation for the central deflection of a spring, also known as the sag, is given by:
δ = (wl^3) / (48EI)
Where δ is the central deflection, w is the load on the spring, l is the span of the spring, E is the modulus of elasticity of the material, and I is the moment of inertia of the cross-sectional area of the spring.
In case of a carriage spring, the moment of inertia is given by
I = b * t^3/12
So the central deflection equation becomes:
δ = (wl^3) / (48E*(b*t^3/12))
which becomes
δ = 3wl^3 / (8Enbt^3)
This is the equation of central deflection, option A.
A close-coifed helical spring of stiffness 4 N/mm is in series with another spring of stiffness 6 N/mm. What is the stiffness of composite spring?- a)5 N/mm
- b)4 N/mm
- c)2.4 N/mm
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A close-coifed helical spring of stiffness 4 N/mm is in series with another spring of stiffness 6 N/mm. What is the stiffness of composite spring?
a)
5 N/mm
b)
4 N/mm
c)
2.4 N/mm
d)
None of these

|
Bibek Mehra answered |
Let the stiffness of composite spring = k
∴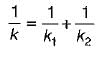
∴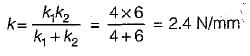
∴
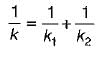
∴
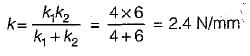
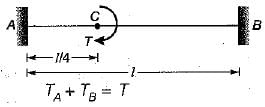
A round shaft of diameter ‘d and length T fixed at both ends A and B is subjected to a twisting moment T at C, at a distance 114 from A. The torsional stresses in the parts AC and CB will be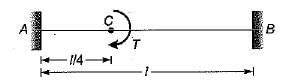
- a)equal
- b)in the ratio of 1 : 3
- c)in the ratio of 3 :1
- d)Indeterminate
Correct answer is option 'C'. Can you explain this answer?
A round shaft of diameter ‘d and length T fixed at both ends A and B is subjected to a twisting moment T at C, at a distance 114 from A. The torsional stresses in the parts AC and CB will be

a)
equal
b)
in the ratio of 1 : 3
c)
in the ratio of 3 :1
d)
Indeterminate

|
Sahil Chawla answered |
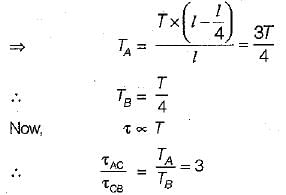
If a shaft is simultaneously subjected to a torque T and a bending moment M, the ratio of maximum bending stress and maximum shearing stress is given by- a)2M/T
- b)M/T
- c)2T/M
- d)T/M
Correct answer is option 'A'. Can you explain this answer?
If a shaft is simultaneously subjected to a torque T and a bending moment M, the ratio of maximum bending stress and maximum shearing stress is given by
a)
2M/T
b)
M/T
c)
2T/M
d)
T/M

|
Prerna Kaur answered |
Ratio of maximum bending stress and maximum shearing stress
The ratio of maximum bending stress and maximum shearing stress in a shaft undergoing simultaneous torque and bending moment can be derived as follows:
Consider a shaft of circular cross-section with radius r, subjected to a torque T and a bending moment M at a distance x from one end. The maximum bending stress and maximum shearing stress occur at the outermost fiber of the shaft.
Maximum bending stress (σb):
The bending stress in a shaft can be calculated using the formula:
σb = M*y/I
where y is the distance from the neutral axis to the outermost fiber, and I is the moment of inertia of the cross-section about the neutral axis.
For a circular cross-section, the moment of inertia is given by:
I = π*r^4/4
Substituting this into the formula for bending stress, we get:
σb = 4*M*y/(π*r^3)
At the outermost fiber, y = r. Therefore, the maximum bending stress is:
σb,max = 4*M/(π*r^2)
Maximum shearing stress (τ):
The shearing stress in a shaft can be calculated using the formula:
τ = T*r/J
where J is the polar moment of inertia of the cross-section.
For a circular cross-section, the polar moment of inertia is given by:
J = π*r^4/2
Substituting this into the formula for shearing stress, we get:
τ = 2*T*r/(π*r^4/2)
Simplifying, we get:
τ = 4*T/(π*r^3)
Therefore, the maximum shearing stress is:
τ,max = 4*T/(π*r^2)
Ratio of maximum bending stress to maximum shearing stress:
Dividing the expression for maximum bending stress by the expression for maximum shearing stress, we get:
σb,max/τ,max = (4*M/(π*r^2))/(4*T/(π*r^2))
Simplifying, we get:
σb,max/τ,max = 2M/T
Therefore, the ratio of maximum bending stress to maximum shearing stress in a shaft undergoing simultaneous torque and bending moment is 2M/T.
Answer: Option A (2M/T)
The ratio of maximum bending stress and maximum shearing stress in a shaft undergoing simultaneous torque and bending moment can be derived as follows:
Consider a shaft of circular cross-section with radius r, subjected to a torque T and a bending moment M at a distance x from one end. The maximum bending stress and maximum shearing stress occur at the outermost fiber of the shaft.
Maximum bending stress (σb):
The bending stress in a shaft can be calculated using the formula:
σb = M*y/I
where y is the distance from the neutral axis to the outermost fiber, and I is the moment of inertia of the cross-section about the neutral axis.
For a circular cross-section, the moment of inertia is given by:
I = π*r^4/4
Substituting this into the formula for bending stress, we get:
σb = 4*M*y/(π*r^3)
At the outermost fiber, y = r. Therefore, the maximum bending stress is:
σb,max = 4*M/(π*r^2)
Maximum shearing stress (τ):
The shearing stress in a shaft can be calculated using the formula:
τ = T*r/J
where J is the polar moment of inertia of the cross-section.
For a circular cross-section, the polar moment of inertia is given by:
J = π*r^4/2
Substituting this into the formula for shearing stress, we get:
τ = 2*T*r/(π*r^4/2)
Simplifying, we get:
τ = 4*T/(π*r^3)
Therefore, the maximum shearing stress is:
τ,max = 4*T/(π*r^2)
Ratio of maximum bending stress to maximum shearing stress:
Dividing the expression for maximum bending stress by the expression for maximum shearing stress, we get:
σb,max/τ,max = (4*M/(π*r^2))/(4*T/(π*r^2))
Simplifying, we get:
σb,max/τ,max = 2M/T
Therefore, the ratio of maximum bending stress to maximum shearing stress in a shaft undergoing simultaneous torque and bending moment is 2M/T.
Answer: Option A (2M/T)
A solid shaft of diameter d is subjected to twisting moment T, such that the maximum shear stress developed is τ. Now a hole of 0.5 d diameter is drilled throdghout the length of the shaft along the axis. How much torque Tmust be reduced so that shear stress remain the same?- a)T/2
- b)T/4
- c)T/8
- d)T/16
Correct answer is option 'D'. Can you explain this answer?
A solid shaft of diameter d is subjected to twisting moment T, such that the maximum shear stress developed is τ. Now a hole of 0.5 d diameter is drilled throdghout the length of the shaft along the axis. How much torque Tmust be reduced so that shear stress remain the same?
a)
T/2
b)
T/4
c)
T/8
d)
T/16

|
Raksha Nair answered |
Given by:
τmax = Tc/J
where c is the radius of the shaft, J is the polar moment of inertia of the shaft (πd^4/32), and τmax is the maximum shear stress.
Therefore, τmax = (16Tc)/(πd^3)
where c = d/2.
So, τmax = (16T)/(πd^3)
τmax = Tc/J
where c is the radius of the shaft, J is the polar moment of inertia of the shaft (πd^4/32), and τmax is the maximum shear stress.
Therefore, τmax = (16Tc)/(πd^3)
where c = d/2.
So, τmax = (16T)/(πd^3)
A circular shaft fixed at A has diameter D for half of its length and diameter D/2 over the other half as shown in the figure. What is the rotation of C relative to B if the rotation of B relative to A is 0.1 radian?
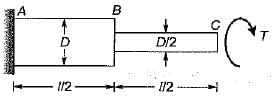
- a)0.4 radian
- b)0.8 radian
- c)1.6 radian
- d)'3.2 radian
Correct answer is option 'C'. Can you explain this answer?
A circular shaft fixed at A has diameter D for half of its length and diameter D/2 over the other half as shown in the figure. What is the rotation of C relative to B if the rotation of B relative to A is 0.1 radian?


a)
0.4 radian
b)
0.8 radian
c)
1.6 radian
d)
'3.2 radian

|
Simran Mukherjee answered |
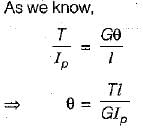
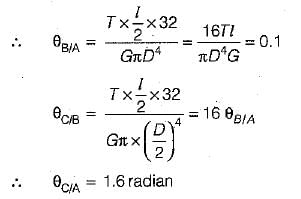
Stiffness of a close-coiled helical spring of wire diameter d, modulus of rigidity G number of coils n, mean coil radius R, is- a)Gd4/64nR3
- b)Gd4/16nR3
- c)Gd4/8nR3
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Stiffness of a close-coiled helical spring of wire diameter d, modulus of rigidity G number of coils n, mean coil radius R, is
a)
Gd4/64nR3
b)
Gd4/16nR3
c)
Gd4/8nR3
d)
None of these

|
Nayanika Joshi answered |
Stiffness of a Close-Coiled Helical Spring
Stiffness or spring constant of a close-coiled helical spring is defined as the force required to produce unit deflection in the spring. It is denoted by k and is given by the formula:
k = (Gd⁴/8nD³) or (Gd⁴/64nR³)
where,
G = modulus of rigidity of the material of the spring
d = diameter of the wire
n = number of coils
D = mean diameter of the spring
R = mean radius of the spring
Explanation
The stiffness of a close-coiled helical spring is directly proportional to the modulus of rigidity of the material of the spring, the fourth power of the wire diameter, and the cube of the mean diameter of the spring. It is inversely proportional to the number of coils and the cube of the mean radius of the spring.
The first formula, k = (Gd⁴/8nD³), is used when the mean diameter of the spring is known. The second formula, k = (Gd⁴/64nR³), is used when the mean radius of the spring is known.
The correct answer is option 'A', i.e., Gd⁴/64nR³. This formula is derived from the formula for the potential energy stored in a spring, which is given by:
U = 1/2 kx²
where,
U = potential energy stored in the spring
k = stiffness or spring constant of the spring
x = deflection of the spring
By differentiating this formula with respect to x, we get the formula for the force required to produce unit deflection in the spring, which is given by:
F = kx
Substituting the value of k from the formula mentioned above, we get:
F = (Gd⁴/8nD³) x or F = (Gd⁴/64nR³) x
Hence, the correct answer is option 'A', i.e., Gd⁴/64nR³.
Stiffness or spring constant of a close-coiled helical spring is defined as the force required to produce unit deflection in the spring. It is denoted by k and is given by the formula:
k = (Gd⁴/8nD³) or (Gd⁴/64nR³)
where,
G = modulus of rigidity of the material of the spring
d = diameter of the wire
n = number of coils
D = mean diameter of the spring
R = mean radius of the spring
Explanation
The stiffness of a close-coiled helical spring is directly proportional to the modulus of rigidity of the material of the spring, the fourth power of the wire diameter, and the cube of the mean diameter of the spring. It is inversely proportional to the number of coils and the cube of the mean radius of the spring.
The first formula, k = (Gd⁴/8nD³), is used when the mean diameter of the spring is known. The second formula, k = (Gd⁴/64nR³), is used when the mean radius of the spring is known.
The correct answer is option 'A', i.e., Gd⁴/64nR³. This formula is derived from the formula for the potential energy stored in a spring, which is given by:
U = 1/2 kx²
where,
U = potential energy stored in the spring
k = stiffness or spring constant of the spring
x = deflection of the spring
By differentiating this formula with respect to x, we get the formula for the force required to produce unit deflection in the spring, which is given by:
F = kx
Substituting the value of k from the formula mentioned above, we get:
F = (Gd⁴/8nD³) x or F = (Gd⁴/64nR³) x
Hence, the correct answer is option 'A', i.e., Gd⁴/64nR³.
The diameter of shaft B is twice that of shaft A Both shafts have the same length and are of the same material, if both are subjected to same torque, then the ratio of the angle of twist of shaft' A to that of shaft B will be- a)2
- b)4
- c)8
- d)16
Correct answer is option 'D'. Can you explain this answer?
The diameter of shaft B is twice that of shaft A Both shafts have the same length and are of the same material, if both are subjected to same torque, then the ratio of the angle of twist of shaft' A to that of shaft B will be
a)
2
b)
4
c)
8
d)
16

|
Megha Choudhury answered |
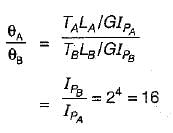
Wahl’s factor takes into account- a)Curvature of the helical wire
- b)Direct shear stress
- c)Both curvature and direct shear effect
- d)Neither (a) nor (b)
Correct answer is option 'C'. Can you explain this answer?
Wahl’s factor takes into account
a)
Curvature of the helical wire
b)
Direct shear stress
c)
Both curvature and direct shear effect
d)
Neither (a) nor (b)

|
Aaditya Jain answered |
Wahl is a company that specializes in producing hair clippers, trimmers, shavers, and other grooming products. The company was founded in 1919 by Leo J. Wahl in Sterling, Illinois. Today, Wahl is one of the largest manufacturers of hair clippers in the world and their products are used by barbers, hairdressers, and consumers worldwide. The company is known for its quality, durability, and innovation, and has won numerous awards for its products.
Two shaft of same material and same length are connected in series and subjected to a torque T as shown in the figure given below?
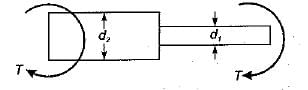
If d2/d1 = 2, what is the value of τ1/τ2?
(where τ1 and τ2 are extreme shear stresses in either of the two segments)
- a)4
- b)2
- c)8
- d)16
Correct answer is option 'C'. Can you explain this answer?
Two shaft of same material and same length are connected in series and subjected to a torque T as shown in the figure given below?

If d2/d1 = 2, what is the value of τ1/τ2?
(where τ1 and τ2 are extreme shear stresses in either of the two segments)

If d2/d1 = 2, what is the value of τ1/τ2?
(where τ1 and τ2 are extreme shear stresses in either of the two segments)
a)
4
b)
2
c)
8
d)
16

|
Gate Funda answered |


Chapter doubts & questions for Torsion of Shafts - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Torsion of Shafts - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
6 Months Preparation for GATE Civil Engg
488 videos|1261 docs|878 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup

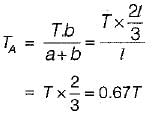

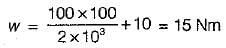
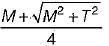
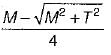
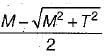
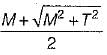
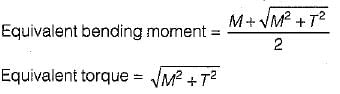
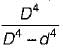
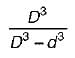
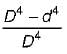
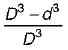
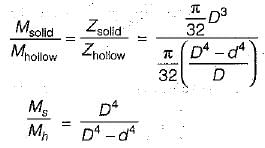
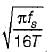
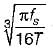
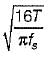
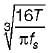
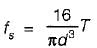
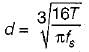
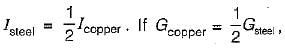 what is the ratio of
what is the ratio of 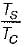 if composite shaft is subjected to a twisting moment?
if composite shaft is subjected to a twisting moment?