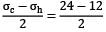All Exams >
Civil Engineering (CE) >
6 Months Preparation for GATE Civil Engg >
All Questions
All questions of Thin & Thick Cylinders for Civil Engineering (CE) Exam
A thin cylindrical shell of diameter 200 mm, thickness 8 mm is held between two rigid supports as shown in figure. An internal pressure of 5 N/mm2 is applied on the inner surface of the cylinder. The resultant axial stresses developed in the cylinder (μ = 0.35) is _________MPa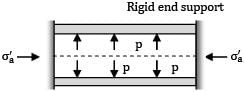 (A) 21.0(B) 22.5
(A) 21.0(B) 22.5
Correct answer is option ''. Can you explain this answer?
A thin cylindrical shell of diameter 200 mm, thickness 8 mm is held between two rigid supports as shown in figure. An internal pressure of 5 N/mm2 is applied on the inner surface of the cylinder. The resultant axial stresses developed in the cylinder (μ = 0.35) is _________MPa

(A) 21.0
(B) 22.5
|
|
Neha Joshi answered |
Stresses developed
σc =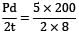 = 62.5 N/mm2
= 62.5 N/mm2
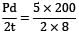 = 62.5 N/mm2
= 62.5 N/mm2σa =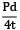 = 31.25 N/mm2
= 31.25 N/mm2
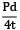 = 31.25 N/mm2
= 31.25 N/mm2Due to rigid end supports, axial strain, εa = 0 Say σa′ is axial compressive stress provided by rigid end supports.
Resultant axial stress, σaR = 31.25 − σa′
Axial strain, εa =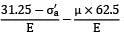 = 0
= 0
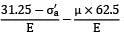 = 0
= 0Or 31.25 − σa′ − 0.35(62.5) = 0
σa′ = 31.25 − 21.875
= 9.375 N/mm2
Resultant axial stress, σaR = 31.25 − 9.375 = 21.875 N/mm2
Question_Type: 5
A thin cylinder contains fluid at a pressure of 500 MN/m2, internal diameter of the shell is 0.6 m and tensile stress in the materials is to be limited to 9000 N/m2. The shell must have a minimum thickness of nearly- a) 9 mm
- b) 11 mm
- c) 17 mm
- d) 21 mm
Correct answer is option 'C'. Can you explain this answer?
A thin cylinder contains fluid at a pressure of 500 MN/m2, internal diameter of the shell is 0.6 m and tensile stress in the materials is to be limited to 9000 N/m2. The shell must have a minimum thickness of nearly
a)
9 mm
b)
11 mm
c)
17 mm
d)
21 mm

|
Pioneer Academy answered |
Σc = 9000
=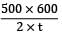
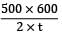
t = 16.66 ≃ 17 mm
In thin cylinder, circumferential stress is x times longitudinal stress, where x is- a) 0.5
- b) 1
- c) 2
- d) 0.2
Correct answer is option 'C'. Can you explain this answer?
In thin cylinder, circumferential stress is x times longitudinal stress, where x is
a)
0.5
b)
1
c)
2
d)
0.2
|
|
Anu Deshpande answered |
Explanation:
Thin Cylinder:
- A thin cylinder is a cylindrical structure with a relatively small wall thickness compared to its radius.
- The wall of a thin cylinder is subjected to both longitudinal stress (along the length of the cylinder) and circumferential stress (around the circumference of the cylinder).
Circumferential Stress vs Longitudinal Stress:
- In a thin cylinder, the circumferential stress (σ_c) is related to the longitudinal stress (σ_l) by a factor x.
- The relationship between circumferential stress and longitudinal stress in a thin cylinder can be expressed as: σ_c = xσ_l.
Understanding x:
- The factor x indicates how much greater the circumferential stress is compared to the longitudinal stress in a thin cylinder.
- For a thin cylinder, x is equal to 2, which means that the circumferential stress is twice the longitudinal stress.
- Therefore, the correct answer is option 'C' which states that x = 2.
Thin Cylinder:
- A thin cylinder is a cylindrical structure with a relatively small wall thickness compared to its radius.
- The wall of a thin cylinder is subjected to both longitudinal stress (along the length of the cylinder) and circumferential stress (around the circumference of the cylinder).
Circumferential Stress vs Longitudinal Stress:
- In a thin cylinder, the circumferential stress (σ_c) is related to the longitudinal stress (σ_l) by a factor x.
- The relationship between circumferential stress and longitudinal stress in a thin cylinder can be expressed as: σ_c = xσ_l.
Understanding x:
- The factor x indicates how much greater the circumferential stress is compared to the longitudinal stress in a thin cylinder.
- For a thin cylinder, x is equal to 2, which means that the circumferential stress is twice the longitudinal stress.
- Therefore, the correct answer is option 'C' which states that x = 2.
A bronze cylinder of diameter 200 mm, wall thickness 8 mm is wound with steel wire of diameter 4 mm under initial tension of 20 N/mm2. The wire wound cylinder is subjected to internal pressure p such that resultant hoop and axial stresses developed in the cylinder are the same. What is the magnitude of p? Given Ew = 210 GPa, EC = 105 GPa, νc = 0.35.- a) 4.58 MPa
- b) 2.32 MPa
- c) 9.16 MPa
- d) 3.26 MPa
Correct answer is option 'A'. Can you explain this answer?
A bronze cylinder of diameter 200 mm, wall thickness 8 mm is wound with steel wire of diameter 4 mm under initial tension of 20 N/mm2. The wire wound cylinder is subjected to internal pressure p such that resultant hoop and axial stresses developed in the cylinder are the same. What is the magnitude of p? Given Ew = 210 GPa, EC = 105 GPa, νc = 0.35.
a)
4.58 MPa
b)
2.32 MPa
c)
9.16 MPa
d)
3.26 MPa
|
|
Zoya Sharma answered |
Σw = 20 N/mm2 dw = 4mm t = 8 mm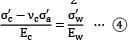
σc = Initial compressive stress in cylinder
= 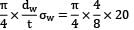
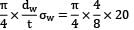
= 7.854 N/mm2 (comp. )
Say internal pressure = P
Axial stress, σa′ =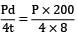 = 6.25 P
= 6.25 P
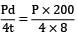 = 6.25 P
= 6.25 PHoop stress = σc′
σCR = (σc′ − 7.854) = 6.25 P, (as given) ⋯ ①
or σc′ = 6.25 P + 7.854 ⋯ ②
Using equilibrium and compatibility conditions
Pd = 2tσc′ +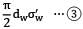
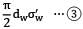
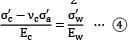
From equation ④
σc′ − νcσ′c = σ′w × 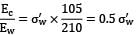
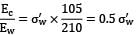
or 6.25 P + 7.854 − 0.35 (6.25 P) = 0.5 σw′
or 4.0625 P + 7.854 = 0.5 σw′
σw′ = 8.125 P + 15.708
Putting the values σw′ and σc′ in equation ③
P × 200 = 2 × 8 × (6.25p + 7.854) + 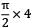 × (8.125p + 15.708)
× (8.125p + 15.708)
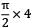 × (8.125p + 15.708)
× (8.125p + 15.708)200P = 100P + 125.664 + 6.283(8.125p + 15.708)
100P = 125.664 + 51.05P + 98.69
48.95 P = 224.354
P = 4.58 N/mm2
When a thin cylinder of diameter ‘d’ and thickness ‘t’ is pressurized with an internal pressure of ‘p’ (1/m is the Poisson’s ratio and E is the modulus of elasticity), then out of the following, which statement is correct?- a) The circumferential strain will be equal to
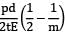
- b) The longitudinal stress will be equal to
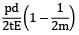
- c) The longitudinal stress will be equal to
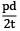
- d) The ratio of the longitudinal strain to circumferential strain will be equal to
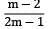
Correct answer is option 'D'. Can you explain this answer?
When a thin cylinder of diameter ‘d’ and thickness ‘t’ is pressurized with an internal pressure of ‘p’ (1/m is the Poisson’s ratio and E is the modulus of elasticity), then out of the following, which statement is correct?
a)
The circumferential strain will be equal to 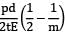
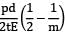
b)
The longitudinal stress will be equal to 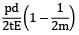
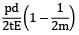
c)
The longitudinal stress will be equal to 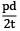
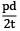
d)
The ratio of the longitudinal strain to circumferential strain will be equal to 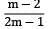
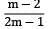
|
|
Lavanya Menon answered |
For a thin cylinder, Longitudinal stress,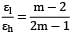
σl =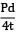
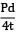
Hoop stress, σn =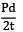
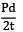
Longitudinal strain,
εl = 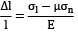
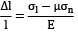
= 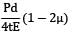
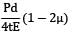
or εl = 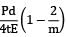
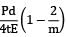
where μ =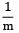
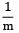
Hoop strain,
εh =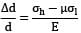
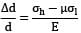
= 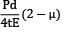
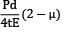
or εh =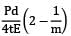
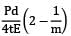
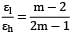
A closed pressure vessel of diameter 120 mm, wall thickness 4 mm is subjected to an internal pressure of 6 N/mm2. The normal stress on an element of cylindrical wall at 30° to the longitudinal axis of cylinder is __________MPa(A) 78.0(B) 79.6
Correct answer is option ''. Can you explain this answer?
A closed pressure vessel of diameter 120 mm, wall thickness 4 mm is subjected to an internal pressure of 6 N/mm2. The normal stress on an element of cylindrical wall at 30° to the longitudinal axis of cylinder is __________MPa
(A) 78.0
(B) 79.6
|
|
Avinash Sharma answered |
Element ab is inclined at an angle of 30° to the axis 00 of the cylinder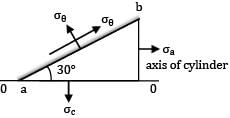

Hoop stress,
σc =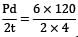 = 90 N/mm2
= 90 N/mm2
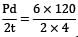 = 90 N/mm2
= 90 N/mm2Axial stress, σa =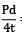 =45 N/mm2
=45 N/mm2
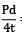 =45 N/mm2
=45 N/mm2Stress on element Normal stress,
σθ =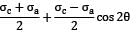
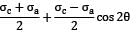
=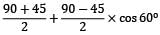
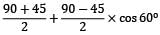
=67.5 + 11.25 = 78. 75 N/mm2
Question_Type: 5
A cylinder of thickness 1.5cm has to withstand maximum internal pressure of 1.5 N/mm2. If the ultimate tensile stress in the material of the cylinder is 300 N/mm2, factor of safety 3.0 and joint efficiency 80%, the diameter of the cylinder is- a) 160 m
- b) 160 cm
- c) 160 mm
- d) 160 km
Correct answer is option 'B'. Can you explain this answer?
A cylinder of thickness 1.5cm has to withstand maximum internal pressure of 1.5 N/mm2. If the ultimate tensile stress in the material of the cylinder is 300 N/mm2, factor of safety 3.0 and joint efficiency 80%, the diameter of the cylinder is
a)
160 m
b)
160 cm
c)
160 mm
d)
160 km
|
|
Sanvi Kapoor answered |
300/3 =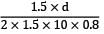
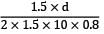
d = 1600 mm = 160 cm
In a thin cylinder, hoop stress is 48 N/mm2. The max. Shear stress developed in the pipe material is- a) 17 N/mm2
- b) 15 N/mm2
- c) 40 N/mm2
- d) 12 N/mm2
Correct answer is option 'D'. Can you explain this answer?
In a thin cylinder, hoop stress is 48 N/mm2. The max. Shear stress developed in the pipe material is
a)
17 N/mm2
b)
15 N/mm2
c)
40 N/mm2
d)
12 N/mm2
|
|
Avinash Sharma answered |
Σh = 48 N/mm2 , σlongitudinal = σl = 24 N/mm2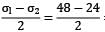
Max shear stress,
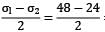
=12N/mm2
A 600 mm diameter pipe contains a fluid at a pressure of 3 N/mm2. If the safe stress in tension is 75 N/mm2, the minimum thickness of pipe is equal to- a) 12 mm
- b) 10 mm
- c) 13.2 mm
- d) 11.25mm
Correct answer is option 'A'. Can you explain this answer?
A 600 mm diameter pipe contains a fluid at a pressure of 3 N/mm2. If the safe stress in tension is 75 N/mm2, the minimum thickness of pipe is equal to
a)
12 mm
b)
10 mm
c)
13.2 mm
d)
11.25mm
|
|
Zoya Sharma answered |
Diameter, d = 600mm Pressure,
P = 3 N/mm2 Safe
streee = 75 N/mm2 Minimum thickness, t =?
75 =

t = 12mm
A thin cylindrical shell of diameter ‘d’, length ‘l’ and thickness ‘t’ is subjected to an internal pressure ‘p’. What is the ratio of longitudinal strain to hoop strain in terms of Poisson’s ratio (1/m)?- a)
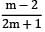
- b)
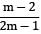
- c)
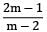
- d)
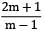
Correct answer is option 'B'. Can you explain this answer?
A thin cylindrical shell of diameter ‘d’, length ‘l’ and thickness ‘t’ is subjected to an internal pressure ‘p’. What is the ratio of longitudinal strain to hoop strain in terms of Poisson’s ratio (1/m)?
a)
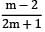
b)
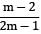
c)
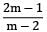
d)
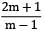

|
Naroj Boda answered |
For a thin cylinder, longitudinal strain,
εl = 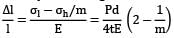
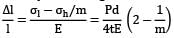
Now,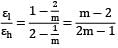
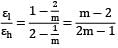
When is the safe working pressure for a spherical pressure vessel 1.5 m internal diameter and 1.5 cm wall thickness if the maximum allowable tensile stress in vessel is 45 MPa?- a) 0.9 MPa
- b) 3.6 MPa
- c) 2.7 MPa
- d) 1.8 MPa
Correct answer is option 'D'. Can you explain this answer?
When is the safe working pressure for a spherical pressure vessel 1.5 m internal diameter and 1.5 cm wall thickness if the maximum allowable tensile stress in vessel is 45 MPa?
a)
0.9 MPa
b)
3.6 MPa
c)
2.7 MPa
d)
1.8 MPa
|
|
Zoya Sharma answered |
Σall = 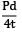
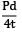
P = = 1.8 MPa
= 1.8 MPa
 = 1.8 MPa
= 1.8 MPa A thin cylinder of radius r and thickness t when subjected to an internal hydrostatic pressure P causes a radial displacement u, then the tangential strain caused is- a) du/dr
- b) 1/r du/dr
- c) u/r
- d) 2u/r
Correct answer is option 'C'. Can you explain this answer?
A thin cylinder of radius r and thickness t when subjected to an internal hydrostatic pressure P causes a radial displacement u, then the tangential strain caused is
a)
du/dr
b)
1/r du/dr
c)
u/r
d)
2u/r
|
|
Neha Joshi answered |
The thin walled pressure vessel expands when it is internally pressurized. This results in three principal strains, the circumferential strain (εc) or tangential strain in two perpendicular plane directions, and the radial strain εr .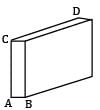
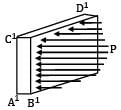



Referring to the figure which shows strain of an element at the surface of the cylinder, we can write.
εc = 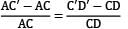
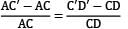
and εr =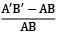
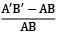
To determine the amount by which the vessel expands, consider a circumference at radius r and which moves out with a displacementδr. From the definition of normal strain,

εc =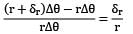
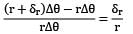
here δr = u
⇒ εc = 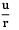
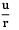
This is the circumferential strain.
Match List-I with List-II and select the correct answer using the code given below the lists.List-I List –II(state of stress) (kind of loading)(a)  1. Combined bending and torsion of circular shaft(b)
1. Combined bending and torsion of circular shaft(b)  2. Torsion of circular shaft(c)
2. Torsion of circular shaft(c) 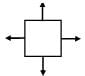 3. Thin cylinder subjected to internal pressure(d)
3. Thin cylinder subjected to internal pressure(d)  4. Tie bar subjected to tensile forceCodes: a b c d
4. Tie bar subjected to tensile forceCodes: a b c d- a) 2 1 3 4
- b) 3 4 2 1
- c) 2 4 3 1
- d) 3 1 2 4
Correct answer is option 'C'. Can you explain this answer?
Match List-I with List-II and select the correct answer using the code given below the lists.
List-I List –II
(state of stress) (kind of loading)
(a)  1. Combined bending and torsion of circular shaft
1. Combined bending and torsion of circular shaft
 1. Combined bending and torsion of circular shaft
1. Combined bending and torsion of circular shaft(b)  2. Torsion of circular shaft
2. Torsion of circular shaft
 2. Torsion of circular shaft
2. Torsion of circular shaft(c)  3. Thin cylinder subjected to internal pressure
3. Thin cylinder subjected to internal pressure
 3. Thin cylinder subjected to internal pressure
3. Thin cylinder subjected to internal pressure(d)  4. Tie bar subjected to tensile force
4. Tie bar subjected to tensile force
 4. Tie bar subjected to tensile force
4. Tie bar subjected to tensile forceCodes: a b c d
a)
2 1 3 4
b)
3 4 2 1
c)
2 4 3 1
d)
3 1 2 4

|
Pioneer Academy answered |
(i) Tie bar subjected to tensile force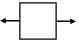
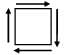
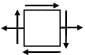

(ii) Thin cylinder subjected to internal pressure σx = σ1 =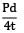
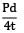
σy = σ2 =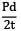
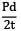

(iii) Torsion of circular shaft is a case of pure shear.

(iv) Combined bending and torsion of circular shaft In this case both normal as well as shear stress act on the element.

Circumferential stress in a cylindrical steel boiler shell under internal pressure is 80MPa. Young’s modulus of elasticity and Poisson’s ratio are respectively 2 × 105 MPa and 0.28. The magnitude of circumferential strain in the boiler shell be- a) 3.44 × 10−4
- b) 3.84 × 10−4
- c) 4 × 10−4
- d) 4.56 × 10−4
Correct answer is option 'A'. Can you explain this answer?
Circumferential stress in a cylindrical steel boiler shell under internal pressure is 80MPa. Young’s modulus of elasticity and Poisson’s ratio are respectively 2 × 105 MPa and 0.28. The magnitude of circumferential strain in the boiler shell be
a)
3.44 × 10−4
b)
3.84 × 10−4
c)
4 × 10−4
d)
4.56 × 10−4
|
|
Neha Joshi answered |
Circumferential stress or Hoop stress,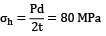
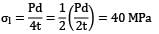
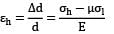
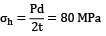
Longitudinal stress,
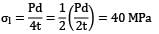
Circumferential strain,
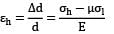
= 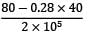
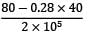
= 3.44 × 10−4
A thin walled pressure vessel made of aluminium alloy, 250 mm diameter and 4 mm thick is subjected to an internal pressure of 2.5 N/mm2. Strain gauges mounted on the surface of vessel in circumferential and axial directions give readings of 932 μs and 190 μs respectively, under full pressure, The young’s modulus of the aluminium alloy is _________Gpa - a)69.0
- b)71.0
Correct answer is option 'A'. Can you explain this answer?
A thin walled pressure vessel made of aluminium alloy, 250 mm diameter and 4 mm thick is subjected to an internal pressure of 2.5 N/mm2. Strain gauges mounted on the surface of vessel in circumferential and axial directions give readings of 932 μs and 190 μs respectively, under full pressure, The young’s modulus of the aluminium alloy is _________Gpa
a)
69.0
b)
71.0

|
Pioneer Academy answered |
P = 2.5 N/mm2
d = 250 mm t = 4 mm εc ,
Circumferential stress
= 

εa , axial strain =

= 190 × 10−6 ⋯ ②
Dividing equation ① by equation ②
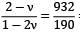 = 4.905
= 4.905or 2 − ν = 4.905 − 9.81 ν 8.81 ν = 2.905
Poisson’s ratio, ν =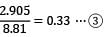
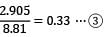
From equation ①
E =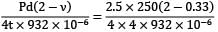
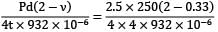
= 69994 N/mm2 = 69.99 GPa
Question_Type: 5
A pressure vessel in the form of a thin cylinder of 1 m diameter and 1mm plate thickness is subjected to an internal fluid pressure of 0.2MPa. The maximum shear stress in the material is- a) 37.5 MPa
- b) 0 MPa
- c) 25 MPa
- d) 50 MPa
Correct answer is option 'D'. Can you explain this answer?
A pressure vessel in the form of a thin cylinder of 1 m diameter and 1mm plate thickness is subjected to an internal fluid pressure of 0.2MPa. The maximum shear stress in the material is
a)
37.5 MPa
b)
0 MPa
c)
25 MPa
d)
50 MPa
|
|
Avinash Sharma answered |
D = 1 m = 103 mm t = 1 mm P = 0.2 MPa
τmax =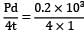
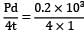
= 50 MPa
A thin cylinder 150 mm internal diameter and 2.5 mm thick has its ends closed by rigid plates and is then filled with water under pressure. When an axial pull of 37 kN is applied to the ends, water pressure is observed to fall by 0.1 N/mm2. The Poisson’s ratio will be (Assume E = 140000 N/mm2, K for water = 2200 N/mm2)- a) 0.31
- b) 0.28
- c) 0.25
- d) 0.36
Correct answer is option 'A'. Can you explain this answer?
A thin cylinder 150 mm internal diameter and 2.5 mm thick has its ends closed by rigid plates and is then filled with water under pressure. When an axial pull of 37 kN is applied to the ends, water pressure is observed to fall by 0.1 N/mm2. The Poisson’s ratio will be (Assume E = 140000 N/mm2, K for water = 2200 N/mm2)
a)
0.31
b)
0.28
c)
0.25
d)
0.36
|
|
Neha Joshi answered |
Δp = 0.1 N/mm2
Reduction in volumetric strain of cylinder
= 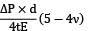
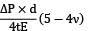
Reduction in volumetric strain of water
= 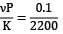
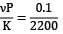
Axial force = 37000 N
Axial stress =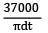
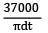
= 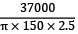
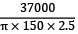
= 31.406 N/mm2
Increase in volumetric strain due to pull
= 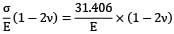
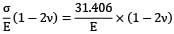
Or 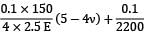
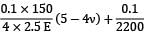
= 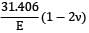
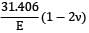
Or 1.5(5 − 4ν) +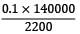
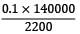
= 31.406 (1 − 2ν)
7.5 − 6ν + 6.3636 = 31.406 − 62.812ν
Or 56.812 ν = 31.406 − 6.3636 − 7.5
= 17.5424
Poisson’s ratio,
ν = = 0.308
= 0.308
 = 0.308
= 0.308A thin cylindrical shell made of steel, of diameter 250 mm, wall thickness 6 mm, length 1 m is subjected to internal pressure p such that maximum stress developed in the shell is 120 MPa. If E = 200 GPa and Poisson’s ratio is 0.3. The change in volume of the shell is ___________ cm3 - a)55.5
- b)56.5
- c)55.96
- d)none
Correct answer is option 'C'. Can you explain this answer?
A thin cylindrical shell made of steel, of diameter 250 mm, wall thickness 6 mm, length 1 m is subjected to internal pressure p such that maximum stress developed in the shell is 120 MPa. If E = 200 GPa and Poisson’s ratio is 0.3. The change in volume of the shell is ___________ cm3
a)
55.5
b)
56.5
c)
55.96
d)
none
|
|
Avinash Sharma answered |
Maximum stress,
σc = 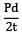 = = 120 N/mm2
= = 120 N/mm2
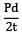 = = 120 N/mm2
= = 120 N/mm2P= 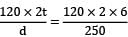 = 5.76 N/mm2
= 5.76 N/mm2
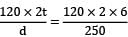 = 5.76 N/mm2
= 5.76 N/mm2E = 200000 N/mm2 , ν = 0.3
Axial strain,
εa =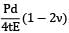
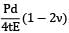
= 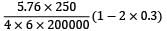
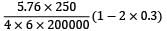
= 1.2 × 10−4
Circumferential strain,
εc =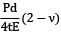
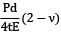
= 

= 5.1 × 10−4
Volumetric strain, εv = 2εc + εa
= 2 × 5.1 × 10−4 + 1.2 × 10−4
= 11.4 × 10−4
Original volume,
V =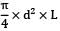
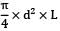
=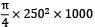
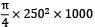
= 49.0874 × 106 mm3
Change in volume, δV = εv × V
= 11.4 × 10−4 × 49.0874 × 106
= 55960 mm3 = 55.96 cm3
= 55.96 cc
Question_Type: 5
A thin cylinder with both ends closed is subjected to internal pressure p. The longitudinal stress at the surface has been calculated as σ0 . Maximum shear stress at the surface will be- a) 2 σ0
- b) 1.5 σ0
- c) σ0
- d) None of these
Correct answer is option 'C'. Can you explain this answer?
A thin cylinder with both ends closed is subjected to internal pressure p. The longitudinal stress at the surface has been calculated as σ0 . Maximum shear stress at the surface will be
a)
2 σ0
b)
1.5 σ0
c)
σ0
d)
None of these
|
|
Sanvi Kapoor answered |
At the surface σa = σ0 σc = 2σ0 P = 0 (radial stress)
τmax = 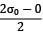 = σ0
= σ0
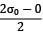 = σ0
= σ0 A cylindrical steel pressure vessel 400mm in diameter with a wall thickness of 20mm is subjected to an internal pressure of 4.5 MPa. Calculate the circumferential stresses (σx ) and longitudinal stresses (σy ) in the steel vessel.- a) σx = 45 MPa, σy = 22.5 MPa
- b) σx = 22.5 MPa, σy = 45 MPa
- c) σx = 45 MPa, σy = 90 MPa
- d) σx = 90 MPa, σy = 45 MPa
Correct answer is option 'A'. Can you explain this answer?
A cylindrical steel pressure vessel 400mm in diameter with a wall thickness of 20mm is subjected to an internal pressure of 4.5 MPa. Calculate the circumferential stresses (σx ) and longitudinal stresses (σy ) in the steel vessel.
a)
σx = 45 MPa, σy = 22.5 MPa
b)
σx = 22.5 MPa, σy = 45 MPa
c)
σx = 45 MPa, σy = 90 MPa
d)
σx = 90 MPa, σy = 45 MPa
|
|
Sarita Yadav answered |
Diameter = 400mm t = 20mm
p = 4.5 MPa
Circumferential stresses,
σx = 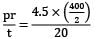
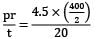
σx = 45 MPa
Longitudinal stresses,
σy = 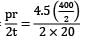
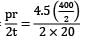
σy = 22.5 MPa
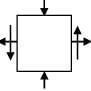
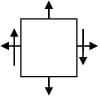
A thin cylinder with closed ends is subjected to internal pressure and supported at ends as shown in figure. What is the state of stress at point x?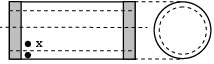
Correct answer is option 'A'. Can you explain this answer?
A thin cylinder with closed ends is subjected to internal pressure and supported at ends as shown in figure. What is the state of stress at point x?





|
|
Zoya Sharma answered |
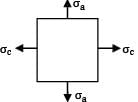
No. shear stress, τ Hoop and axial stresses act, both are tensile.
In case of thin walled cylinder the ratio of hoop strain to Volumetric strain is- a)

- b)
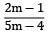
- c)
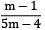
- d)

Correct answer is option 'B'. Can you explain this answer?
In case of thin walled cylinder the ratio of hoop strain to Volumetric strain is
a)

b)
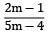
c)
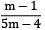
d)

|
|
Avinash Sharma answered |
Hoop strain,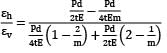
εh = 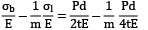
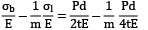
Longitudinal strain,
εl =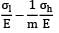
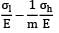
= 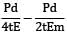
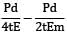
Volumetric strain,
εv = εl + 2εb
= 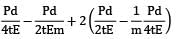
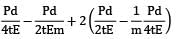
= 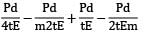
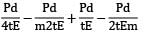
εv= 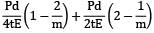
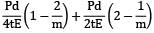
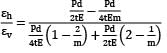
= 

= 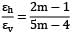
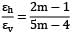
A cylinder of internal diameter 2.5m and of thickness 5cm contains a gas. If the tensile stress in the material is not to exceed 80 N/mm2, the internal pressure of the gas should be- a) 3.2 N/mm2
- b) 6.4 N/mm2
- c) 7.2 N/mm2
- d) 1.6 N/mm2
Correct answer is option 'A'. Can you explain this answer?
A cylinder of internal diameter 2.5m and of thickness 5cm contains a gas. If the tensile stress in the material is not to exceed 80 N/mm2, the internal pressure of the gas should be
a)
3.2 N/mm2
b)
6.4 N/mm2
c)
7.2 N/mm2
d)
1.6 N/mm2
|
|
Sanvi Kapoor answered |
80 = 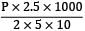
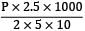
P= 3.2 N/mm2
If the cylindrical pipe is subjected to internal fluid pressure, the nature of hoop stress is- a) Shear
- b) Compression
- c) Tension
- d) Any one
Correct answer is option 'C'. Can you explain this answer?
If the cylindrical pipe is subjected to internal fluid pressure, the nature of hoop stress is
a)
Shear
b)
Compression
c)
Tension
d)
Any one
|
|
Avinash Sharma answered |
Hoop stress acts along the circumference this stress is tensile in nature.
What is the safe working pressure for a spherical pressure vessel 1.5m internal diameter and 1.5cm wall thickness, if the maximum allowable tensile stress is 45 MPa?- a) 0.9 MPa
- b) 3.6 MPa
- c) 2.7 MPa
- d) 1.8 MPa
Correct answer is option 'D'. Can you explain this answer?
What is the safe working pressure for a spherical pressure vessel 1.5m internal diameter and 1.5cm wall thickness, if the maximum allowable tensile stress is 45 MPa?
a)
0.9 MPa
b)
3.6 MPa
c)
2.7 MPa
d)
1.8 MPa
|
|
Neha Joshi answered |
Hoop stress ≤ Maximum allowable tensile stress (for spherical vessel)



P ≤ 1.8 MPa For safe working, pressure should be less than 1.8 MPa
A water tank, 7000 mm in diameter, is made from steel plates that are 15 mm. thick. Find the maximum height to which the tank may be filled if the circumferential stress is limited to 40 MPa. The specific weight of water is 9800 N/m3- a) 17.5 m
- b) 8.75 m
- c) 12.56 m
- d) 10.45 m
Correct answer is option 'A'. Can you explain this answer?
A water tank, 7000 mm in diameter, is made from steel plates that are 15 mm. thick. Find the maximum height to which the tank may be filled if the circumferential stress is limited to 40 MPa. The specific weight of water is 9800 N/m3
a)
17.5 m
b)
8.75 m
c)
12.56 m
d)
10.45 m
|
|
Sarita Yadav answered |
Diameter = 7000 mm t = 15mm Pressure of water = rh = 9800 h N/m2
Maximum circumferential stress,
=  = 40 MPa
= 40 MPa
 = 40 MPa
= 40 MPa40 = 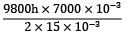
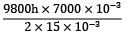
h = 8.75m × 2 = 17.5m
A pipe having internal diameter d, wall thickness t and internal pressure p, the bursting pressure is- a)
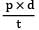
- b)
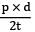
- c)
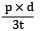
- d)
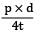
Correct answer is option 'B'. Can you explain this answer?
A pipe having internal diameter d, wall thickness t and internal pressure p, the bursting pressure is
a)
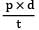
b)
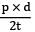
c)
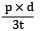
d)
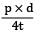

|
Saif Ahmed answered |
Its Hoop Stress formula for cylinder.. Question is incomplete
Maximum value of shear stress in thin cylinders is equal to- a)2 (hoop stress)
- b)0.5 (hoop stress)
- c)Hoop stress
- d)0.25 (hoop stress)
Correct answer is option 'D'. Can you explain this answer?
Maximum value of shear stress in thin cylinders is equal to
a)
2 (hoop stress)
b)
0.5 (hoop stress)
c)
Hoop stress
d)
0.25 (hoop stress)

|
Pk Academy answered |
For a thin-walled cylinder with internal pressure:
Hoop Stress (σₕ) acts around the circumference. Longitudinal Stress (σ_L) acts along the length, which is half of σₕ, so σ_L = σₕ⁄2.
Maximum shear stress (τ_max) is calculated as (σₕ - σ_L)⁄2. Substituting σ_L:
τ_max = (σₕ - σₕ⁄2)⁄2 = σₕ⁄4.
Thus, the maximum shear stress is 0.25 times the hoop stress.
Answer:
d) 0.25 (hoop stress)
d) 0.25 (hoop stress)
If the hoop strain and longitudinal strain in case of a thin cylindrical shell are eh and et then volumetric strain is- a) eh + et
- b) eh + 2et
- c) 2 (eh + et)
- d) 2eh + et
Correct answer is option 'D'. Can you explain this answer?
If the hoop strain and longitudinal strain in case of a thin cylindrical shell are eh and et then volumetric strain is
a)
eh + et
b)
eh + 2et
c)
2 (eh + et)
d)
2eh + et

|
Amar Desai answered |
Explanation:
When a thin cylindrical shell undergoes deformation, it experiences hoop strain (eh) and longitudinal strain (et). The volumetric strain is the sum of these two strains and can be calculated as follows:
Volumetric strain = eh + et
However, this formula only holds for isotropic materials. In the case of non-isotropic materials, the volumetric strain can be calculated using the following formula:
Volumetric strain = 2eh + et
This is because the material may have different properties in the hoop and longitudinal directions, resulting in different levels of deformation in each direction.
Therefore, in the given question, since we are dealing with a thin cylindrical shell which is a non-isotropic material, the correct answer is option D, which is 2eh - et.
When a thin cylindrical shell undergoes deformation, it experiences hoop strain (eh) and longitudinal strain (et). The volumetric strain is the sum of these two strains and can be calculated as follows:
Volumetric strain = eh + et
However, this formula only holds for isotropic materials. In the case of non-isotropic materials, the volumetric strain can be calculated using the following formula:
Volumetric strain = 2eh + et
This is because the material may have different properties in the hoop and longitudinal directions, resulting in different levels of deformation in each direction.
Therefore, in the given question, since we are dealing with a thin cylindrical shell which is a non-isotropic material, the correct answer is option D, which is 2eh - et.
Chapter doubts & questions for Thin & Thick Cylinders - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Thin & Thick Cylinders - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
6 Months Preparation for GATE Civil Engg
488 videos|1261 docs|878 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup