All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Regular Expressions, Languages, Grammar & Finite Automata for Computer Science Engineering (CSE) Exam
Assume the R is a relation on a set A, aRb is partially ordered such that a and b are _____________- a)reflexive
- b)transitive
- c)symmetric
- d)reflexive and transitive
Correct answer is option 'D'. Can you explain this answer?
Assume the R is a relation on a set A, aRb is partially ordered such that a and b are _____________
a)
reflexive
b)
transitive
c)
symmetric
d)
reflexive and transitive

|
Swara Dasgupta answered |
A partially ordered relation refers to one which is Reflexive, Transitive and Antisymmetric.
Which of the following is a correct statement?
- a)Moore machine has no accepting states
- b)Mealy machine has accepting states
- c)Both (A) and (B)
- d)All of the mentioned
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a correct statement?
a)
Moore machine has no accepting states
b)
Mealy machine has accepting states
c)
Both (A) and (B)
d)
All of the mentioned
|
|
Ujwal Roy answered |
Answer: C
Explanation: Statement a and b is correct while c is false. Finite machines with output have no accepting states and can be converted within each other.
Explanation: Statement a and b is correct while c is false. Finite machines with output have no accepting states and can be converted within each other.
Which of the following is an application of Finite Automaton?- a)Compiler Design
- b)Grammar Parsers
- c)Text Search
- d)All of the mentioned
Correct answer is option 'D'. Can you explain this answer?
Which of the following is an application of Finite Automaton?
a)
Compiler Design
b)
Grammar Parsers
c)
Text Search
d)
All of the mentioned

|
Shivam Sharma answered |
There are many applications of finite automata, mainly in the field of Compiler Design and Parsers and Search Engines.
What is the output for the given language?
Language: A set of strings over ∑= {a, b} is taken as input and it prints 1 as an output “for every occurrence of a, b as its substring. (INPUT: abaaab)- a)0010001
- b)0101010
- c)0111010
- d)0010000
Correct answer is option 'A'. Can you explain this answer?
What is the output for the given language?
Language: A set of strings over ∑= {a, b} is taken as input and it prints 1 as an output “for every occurrence of a, b as its substring. (INPUT: abaaab)
Language: A set of strings over ∑= {a, b} is taken as input and it prints 1 as an output “for every occurrence of a, b as its substring. (INPUT: abaaab)
a)
0010001
b)
0101010
c)
0111010
d)
0010000
|
|
Prasad Unni answered |
The outputs are as per the input, produced.
Which of the following x is accepted by the given DFA (x is a binary string ∑= {0,1})?
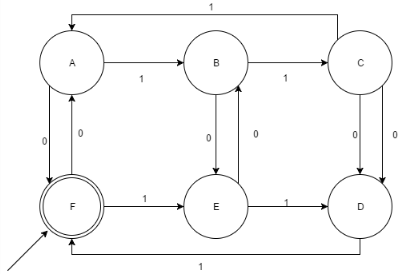
- a)divisible by 3
- b)divisible by 2
- c)divisible by 1 and 3
- d)divisible by 3 and 2
Correct answer is option 'D'. Can you explain this answer?
Which of the following x is accepted by the given DFA (x is a binary string ∑= {0,1})?
a)
divisible by 3
b)
divisible by 2
c)
divisible by 1 and 3
d)
divisible by 3 and 2
|
|
Lekshmi Shah answered |
Correct Answer :- d
Explanation : The given DFA accepts all the binary strings such that they are divisible by 3 and 2.Thus, it can be said that it also accepts all the strings which is divisible by 6.
δ(A,1) = B, δ(A,0) =A
Δ (B, (0,1)) =C
δ(C,0) = A (Initial state =A)
String=”011001” is transit at which of the states?- a)A
- b)C
- c)B
- d)Invalid String
Correct answer is option 'A'. Can you explain this answer?
δ(A,1) = B, δ(A,0) =A
Δ (B, (0,1)) =C
δ(C,0) = A (Initial state =A)
String=”011001” is transit at which of the states?
Δ (B, (0,1)) =C
δ(C,0) = A (Initial state =A)
String=”011001” is transit at which of the states?
a)
A
b)
C
c)
B
d)
Invalid String
|
|
Abhay Ghoshal answered |
For a string of n characters with no repetitive substrings, the number of states required to pass the string is n+1.
Given: ∑= {a, b}
L= {xϵ∑*|x is a string combination}
∑4 represents which among the following?- a){aa, ab, ba, bb}
- b){aaaa, abab, ε, abaa, aabb}
- c){aaa, aab, aba, bbb}
- d)All of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Given: ∑= {a, b}
L= {xϵ∑*|x is a string combination}
∑4 represents which among the following?
L= {xϵ∑*|x is a string combination}
∑4 represents which among the following?
a)
{aa, ab, ba, bb}
b)
{aaaa, abab, ε, abaa, aabb}
c)
{aaa, aab, aba, bbb}
d)
All of the mentioned
|
|
Sanya Agarwal answered |
Explanation: ∑* represents any combination of the given set while ∑x represents the set of combinations with length x where x ϵ I.
Can a DFA recognize a palindrome number?- a)Yes
- b)No
- c)Yes, with input alphabet as ∑*
- d)Can’t be determined
Correct answer is option 'B'. Can you explain this answer?
Can a DFA recognize a palindrome number?
a)
Yes
b)
No
c)
Yes, with input alphabet as ∑*
d)
Can’t be determined
|
|
Dhruba Goyal answered |
Language to accept a palindrome number or string will be non-regular and thus, its DFA cannot be obtained. Though, PDA is possible.
The non- Kleene Star operation accepts the following string of finite length over set A = {0,1} | where string s contains even number of 0 and 1- a)01,0011,010101
- b)0011,11001100
- c)ε,0011,11001100
- d)ε,0011,11001100
Correct answer is option 'B'. Can you explain this answer?
The non- Kleene Star operation accepts the following string of finite length over set A = {0,1} | where string s contains even number of 0 and 1
a)
01,0011,010101
b)
0011,11001100
c)
ε,0011,11001100
d)
ε,0011,11001100
|
|
Rajeev Menon answered |
The Kleene star of A, denoted by A*, is the set of all strings obtained by concatenating zero or more strings from A.
The minimum number of states required to recognize an octal number divisible by 3 are/is- a)1
- b)3
- c)5
- d)7
Correct answer is option 'B'. Can you explain this answer?
The minimum number of states required to recognize an octal number divisible by 3 are/is
a)
1
b)
3
c)
5
d)
7
|
|
Shounak Yadav answered |
According to the question, minimum of 3 states are required to recognize an octal number divisible by 3.
L1= {w | w does not contain the string tr }
L2= {w | w does contain the string tr}
Given ∑= {t, r}, The difference of the minimum number of states required to form L1 and L2?- a)0
- b)1
- c)2
- d)Cannot be said
Correct answer is option 'A'. Can you explain this answer?
L1= {w | w does not contain the string tr }
L2= {w | w does contain the string tr}
Given ∑= {t, r}, The difference of the minimum number of states required to form L1 and L2?
L2= {w | w does contain the string tr}
Given ∑= {t, r}, The difference of the minimum number of states required to form L1 and L2?
a)
0
b)
1
c)
2
d)
Cannot be said
|
|
Sarthak Chakraborty answered |
Explanation:
DFA Construction:
- To construct a DFA for L1, we need to avoid the string "tr" in the input string.
- So, we can start with an initial state and transition to a new state whenever we encounter 't'. If we encounter 'r' in the new state, we transition back to the initial state.
- For L2, we need to include the string "tr" in the input string.
- We can have a transition from the initial state to a new state on 't' and then transition to another state on 'r' to accept the string.
- The DFA for L1 will have fewer states compared to the DFA for L2.
Minimum Number of States:
- The DFA for L1 can be constructed with 3 states - initial state, state after 't', and a final state.
- The DFA for L2 would require 4 states - initial state, state after 't', state after 'tr', and a final state.
- The difference in the minimum number of states required for L1 and L2 is 1 (4 - 3 = 1).
Therefore, the correct answer is option A) 0.
Which among the following can be an example of application of finite state machine(FSM)?- a)Communication Link
- b)Adder
- c)Stack
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
Which among the following can be an example of application of finite state machine(FSM)?
a)
Communication Link
b)
Adder
c)
Stack
d)
None of the mentioned
|
|
Naina Sharma answered |
Idle is the state when data in form of packets is send and returns if NAK is received else waits for the NAK to be received.
L1= {w | w does not contain the string tr }
L2= {w | w does contain the string tr}
Given ∑= {t, r}, The difference of the minimum number of states required to form L1 and L2?- a)0
- b)1
- c)2
- d)Cannot be said
Correct answer is option 'A'. Can you explain this answer?
L1= {w | w does not contain the string tr }
L2= {w | w does contain the string tr}
Given ∑= {t, r}, The difference of the minimum number of states required to form L1 and L2?
L2= {w | w does contain the string tr}
Given ∑= {t, r}, The difference of the minimum number of states required to form L1 and L2?
a)
0
b)
1
c)
2
d)
Cannot be said
|
|
Kiran Reddy answered |
L1= {w | w does not contain the string tr }
L2= {w | w does contain the string tr}
Given ∑= {t, r}, The difference of the minimum number of states required to form L1 and L2?
L2= {w | w does contain the string tr}
Given ∑= {t, r}, The difference of the minimum number of states required to form L1 and L2?
Which of the following options is correct for the given statement?
Statement: If K is the number of states in NFA, the DFA simulating the same language would have states less than 2k.- a)True
- b)Flase
Correct answer is option 'A'. Can you explain this answer?
Which of the following options is correct for the given statement?
Statement: If K is the number of states in NFA, the DFA simulating the same language would have states less than 2k.
Statement: If K is the number of states in NFA, the DFA simulating the same language would have states less than 2k.
a)
True
b)
Flase
|
|
Swara Basak answered |
If K is the number of states in NFA, the DFA simulating the same language would have states equal to or less than 2k.
In Moore machine, output is produced over the change of:- a)transitions
- b)states
- c)Both
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
In Moore machine, output is produced over the change of:
a)
transitions
b)
states
c)
Both
d)
None of the mentioned
|
|
Athira Choudhary answered |
Moore machine produces an output over the change of transition states while mealy machine does it so for transitions itself.
If L1 and L2 are regular sets then intersection of these two will be- a)Regular
- b)Non Regular
- c)Recursive
- d)Non Recursive
Correct answer is option 'A'. Can you explain this answer?
If L1 and L2 are regular sets then intersection of these two will be
a)
Regular
b)
Non Regular
c)
Recursive
d)
Non Recursive
|
|
Shubham Ghoshal answered |
Regular expression are also colsed under intersection.
Given Language: {x | it is divisible by 3}
The total number of final states to be assumed in order to pass the number constituting {0, 1} is- a)0
- b)1
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
Given Language: {x | it is divisible by 3}
The total number of final states to be assumed in order to pass the number constituting {0, 1} is
The total number of final states to be assumed in order to pass the number constituting {0, 1} is
a)
0
b)
1
c)
2
d)
3
|
|
Akshay Singh answered |
The DFA for the given language can be constructed as follows: 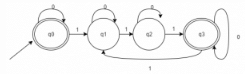
Moore Machine is an application of:- a)Finite automata without input
- b)Finite automata with output
- c)Non- Finite automata with output
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Moore Machine is an application of:
a)
Finite automata without input
b)
Finite automata with output
c)
Non- Finite automata with output
d)
None of the mentioned
|
|
Siddharth Pillai answered |
Finite automaton with an output is categorize din two parts: Moore M/C and Mealy M/C.
The output alphabet can be represented as:- a)δ
- b)∆
- c)∑
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
The output alphabet can be represented as:
a)
δ
b)
∆
c)
∑
d)
None of the mentioned
|
|
Kunal Gupta answered |
Source-The tuple definition of Moore and mealy machine comprises one new member i.e. output alphabet as these are finite machines with output.
The production of form non-terminal -> ε is called:- a)Sigma Production
- b)Null Production
- c)Epsilon Production
- d)All of the mentioned
Correct answer is option 'B'. Can you explain this answer?
The production of form non-terminal -> ε is called:
a)
Sigma Production
b)
Null Production
c)
Epsilon Production
d)
All of the mentioned
|
|
Aarav Malik answered |
The production of form non-terminal ->ε is call null production.
Subset Construction method refers to:- a)Conversion of NFA to DFA
- b)DFA minimization
- c)Eliminating Null references
- d)ε-NFA to NFA
Correct answer is option 'A'. Can you explain this answer?
Subset Construction method refers to:
a)
Conversion of NFA to DFA
b)
DFA minimization
c)
Eliminating Null references
d)
ε-NFA to NFA
|
|
Nandini Joshi answered |
None of the above
The Subset Construction method refers to the conversion of a nondeterministic finite automaton (NFA) to a deterministic finite automaton (DFA).
The Subset Construction method refers to the conversion of a nondeterministic finite automaton (NFA) to a deterministic finite automaton (DFA).
Let N (Q, ∑, δ, q0, A) be the NFA recognizing a language L. Then for a DFA (Q’, ∑, δ’, q0’, A’), which among the following is true?- a)Q’ = P(Q)
- b)Δ’ = δ’ (R, a) = {q ϵ Q | q ϵ δ (r, a), for some r ϵ R}
- c)Q’={q0}
- d)All of the mentioned
Correct answer is option 'D'. Can you explain this answer?
Let N (Q, ∑, δ, q0, A) be the NFA recognizing a language L. Then for a DFA (Q’, ∑, δ’, q0’, A’), which among the following is true?
a)
Q’ = P(Q)
b)
Δ’ = δ’ (R, a) = {q ϵ Q | q ϵ δ (r, a), for some r ϵ R}
c)
Q’={q0}
d)
All of the mentioned
|
|
Jyoti Sengupta answered |
A, T) be the set of all positive integers less than or equal to N that are divisible by either Q, A, or T.
Reverse of (0+1)* will be- a)Phi
- b)Null
- c)(0+1)*
- d)(0+1)
Correct answer is option 'C'. Can you explain this answer?
Reverse of (0+1)* will be
a)
Phi
b)
Null
c)
(0+1)*
d)
(0+1)
|
|
Saanvi Gupta answered |
Explanation:
To find the reverse of a regular language, we need to reverse all the strings in that language. In this case, the regular language is (0 1)*, which represents all possible combinations of 0s and 1s, including the empty string.
Reverse:
To reverse all the strings in the language (0 1)*, we need to reverse each individual string.
Reversing the strings:
Since the language (0 1)* includes the empty string, reversing it will still result in the empty string. Therefore, the reverse of the empty string is the empty string itself.
For the strings that are not empty, we reverse them by reversing the order of the characters. For example, the string "01" will be reversed to "10".
Reverse of (0 1)*:
Now, let's apply the reversal process to the language (0 1)*:
- The empty string is already in its reversed form, which is the empty string itself.
- The string "0" will be reversed to "0".
- The string "1" will be reversed to "1".
- The string "00" will be reversed to "00".
- The string "01" will be reversed to "10".
- The string "10" will be reversed to "01".
- The string "11" will be reversed to "11".
- and so on...
As we can see, the reversed strings are still in the language (0 1)* itself. So, the reverse of (0 1)* is (0 1)*.
Answer:
Therefore, the correct answer is option C, which is (0 1)*.
To find the reverse of a regular language, we need to reverse all the strings in that language. In this case, the regular language is (0 1)*, which represents all possible combinations of 0s and 1s, including the empty string.
Reverse:
To reverse all the strings in the language (0 1)*, we need to reverse each individual string.
Reversing the strings:
Since the language (0 1)* includes the empty string, reversing it will still result in the empty string. Therefore, the reverse of the empty string is the empty string itself.
For the strings that are not empty, we reverse them by reversing the order of the characters. For example, the string "01" will be reversed to "10".
Reverse of (0 1)*:
Now, let's apply the reversal process to the language (0 1)*:
- The empty string is already in its reversed form, which is the empty string itself.
- The string "0" will be reversed to "0".
- The string "1" will be reversed to "1".
- The string "00" will be reversed to "00".
- The string "01" will be reversed to "10".
- The string "10" will be reversed to "01".
- The string "11" will be reversed to "11".
- and so on...
As we can see, the reversed strings are still in the language (0 1)* itself. So, the reverse of (0 1)* is (0 1)*.
Answer:
Therefore, the correct answer is option C, which is (0 1)*.
An e-NFA is ___________ in representation.- a)Quintuple
- b)Quadruple
- c)Triple
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
An e-NFA is ___________ in representation.
a)
Quintuple
b)
Quadruple
c)
Triple
d)
None of the mentioned
|
|
Saanvi Chopra answered |
An e-NFA (epsilon-NFA) is represented using a quintuple, which is a set of five components.
Quintuple Representation:
The quintuple representation of an e-NFA consists of the following components:
1. Set of States (Q): It represents a finite set of states in the e-NFA. Each state is represented by a unique symbol or name. The set of states can be represented as Q = {q0, q1, q2, ...}.
2. Input Alphabet (Σ): It represents a finite set of input symbols or characters that can be read by the e-NFA. The input alphabet can be represented as Σ = {a, b, c, ...}.
3. Transition Function (δ): It represents a function that maps a state and an input symbol to a set of states. The transition function can be represented as δ: Q × Σ → P(Q), where P(Q) represents the power set of Q. For example, δ(q0, a) = {q1, q2} represents that if the e-NFA is in state q0 and reads input symbol 'a', it can transition to states q1 and q2.
4. Initial State (q0): It represents the initial state of the e-NFA. The initial state is a single state from the set of states Q.
5. Set of Final States (F): It represents a set of final or accepting states in the e-NFA. The set of final states can be represented as F = {q3, q4, ...}.
Explanation:
The option 'A' (Quintuple) is the correct answer because an e-NFA is represented using a quintuple, which consists of five components as explained above. The quintuple representation provides a concise and systematic way to define the behavior of an e-NFA.
The other options are not applicable to represent an e-NFA:
- Option 'B' (Quadruple) is incorrect because a quadruple representation is commonly used for representing deterministic finite automata (DFA) and does not capture the additional non-deterministic behavior of an e-NFA.
- Option 'C' (Triple) is incorrect because a triple representation is commonly used for representing regular expressions or regular grammars, which are different formalisms than e-NFAs.
- Option 'D' (None of the mentioned) is incorrect because the representation of an e-NFA requires a formal definition, and the quintuple representation is the standard and widely accepted method for representing an e-NFA.
Quintuple Representation:
The quintuple representation of an e-NFA consists of the following components:
1. Set of States (Q): It represents a finite set of states in the e-NFA. Each state is represented by a unique symbol or name. The set of states can be represented as Q = {q0, q1, q2, ...}.
2. Input Alphabet (Σ): It represents a finite set of input symbols or characters that can be read by the e-NFA. The input alphabet can be represented as Σ = {a, b, c, ...}.
3. Transition Function (δ): It represents a function that maps a state and an input symbol to a set of states. The transition function can be represented as δ: Q × Σ → P(Q), where P(Q) represents the power set of Q. For example, δ(q0, a) = {q1, q2} represents that if the e-NFA is in state q0 and reads input symbol 'a', it can transition to states q1 and q2.
4. Initial State (q0): It represents the initial state of the e-NFA. The initial state is a single state from the set of states Q.
5. Set of Final States (F): It represents a set of final or accepting states in the e-NFA. The set of final states can be represented as F = {q3, q4, ...}.
Explanation:
The option 'A' (Quintuple) is the correct answer because an e-NFA is represented using a quintuple, which consists of five components as explained above. The quintuple representation provides a concise and systematic way to define the behavior of an e-NFA.
The other options are not applicable to represent an e-NFA:
- Option 'B' (Quadruple) is incorrect because a quadruple representation is commonly used for representing deterministic finite automata (DFA) and does not capture the additional non-deterministic behavior of an e-NFA.
- Option 'C' (Triple) is incorrect because a triple representation is commonly used for representing regular expressions or regular grammars, which are different formalisms than e-NFAs.
- Option 'D' (None of the mentioned) is incorrect because the representation of an e-NFA requires a formal definition, and the quintuple representation is the standard and widely accepted method for representing an e-NFA.
How many languages are over the alphabet R?- a)countably infinite
- b)countably finite
- c)uncountable finite
- d)uncountable infinite
Correct answer is option 'D'. Can you explain this answer?
How many languages are over the alphabet R?
a)
countably infinite
b)
countably finite
c)
uncountable finite
d)
uncountable infinite
|
|
Partho Joshi answered |
Answer:
To understand the answer to this question, we first need to clarify what it means for a language to be "over" an alphabet. In the context of formal language theory, an alphabet is a finite set of symbols, and a language is a set of strings made up of those symbols. So, when we say a language is "over" an alphabet, we mean that the strings in the language are composed of symbols from that alphabet.
Countable vs. Uncountable Sets:
In mathematics, there are two types of sets: countable sets and uncountable sets.
- A countable set is one that can be put into a one-to-one correspondence with the natural numbers (1, 2, 3, ...). In other words, the elements of a countable set can be listed in a sequence.
- An uncountable set, on the other hand, is one that cannot be put into a one-to-one correspondence with the natural numbers. Its elements cannot be listed in a sequence.
Countably Infinite Languages:
A language is countably infinite if it can be put into a one-to-one correspondence with the natural numbers. In other words, the strings in the language can be listed in a sequence, where each string corresponds to a natural number.
If the alphabet is finite, then the set of all possible strings over that alphabet is countably infinite. This is because we can list all the strings of length 1, then all the strings of length 2, and so on. Each string can be assigned a unique natural number, and thus the set of all strings is countably infinite.
Uncountable Infinite Languages:
However, if the alphabet is infinite, then the set of all possible strings over that alphabet becomes uncountably infinite. This is because there are infinitely many symbols to choose from for each position in a string, and each position can be assigned a symbol independently.
For example, if the alphabet is the set of real numbers R, then the set of all possible strings over R is uncountably infinite. This is because for each position in a string, we can choose any real number, and there are uncountably many real numbers.
Conclusion:
In the given question, the alphabet is R, which represents the set of real numbers. Since the set of all possible strings over R is uncountably infinite, the correct answer is option 'D' - uncountable infinite.
To understand the answer to this question, we first need to clarify what it means for a language to be "over" an alphabet. In the context of formal language theory, an alphabet is a finite set of symbols, and a language is a set of strings made up of those symbols. So, when we say a language is "over" an alphabet, we mean that the strings in the language are composed of symbols from that alphabet.
Countable vs. Uncountable Sets:
In mathematics, there are two types of sets: countable sets and uncountable sets.
- A countable set is one that can be put into a one-to-one correspondence with the natural numbers (1, 2, 3, ...). In other words, the elements of a countable set can be listed in a sequence.
- An uncountable set, on the other hand, is one that cannot be put into a one-to-one correspondence with the natural numbers. Its elements cannot be listed in a sequence.
Countably Infinite Languages:
A language is countably infinite if it can be put into a one-to-one correspondence with the natural numbers. In other words, the strings in the language can be listed in a sequence, where each string corresponds to a natural number.
If the alphabet is finite, then the set of all possible strings over that alphabet is countably infinite. This is because we can list all the strings of length 1, then all the strings of length 2, and so on. Each string can be assigned a unique natural number, and thus the set of all strings is countably infinite.
Uncountable Infinite Languages:
However, if the alphabet is infinite, then the set of all possible strings over that alphabet becomes uncountably infinite. This is because there are infinitely many symbols to choose from for each position in a string, and each position can be assigned a symbol independently.
For example, if the alphabet is the set of real numbers R, then the set of all possible strings over R is uncountably infinite. This is because for each position in a string, we can choose any real number, and there are uncountably many real numbers.
Conclusion:
In the given question, the alphabet is R, which represents the set of real numbers. Since the set of all possible strings over R is uncountably infinite, the correct answer is option 'D' - uncountable infinite.
An automaton that presents output based on previous state or current input:- a)Acceptor
- b)Classifier
- c)Transducer
- d)None of the mentioned.
Correct answer is option 'C'. Can you explain this answer?
An automaton that presents output based on previous state or current input:
a)
Acceptor
b)
Classifier
c)
Transducer
d)
None of the mentioned.
|
|
Sankar Sarkar answered |
Transducer
Transducer is an automaton that presents output based on previous state or current input. Let's break down this concept further:
Definition:
- A transducer is a device that converts one form of energy into another. In the context of automata theory, a transducer is a type of machine that transforms input symbols into output symbols.
Functionality:
- Transducers have the ability to remember previous states, which allows them to produce output based on both the current input and the history of inputs.
- They can be seen as a combination of a finite state machine and a function that maps input symbols to output symbols.
Example:
- An example of a transducer is a Mealy machine, which is a finite state machine that produces output based on both the current state and the input symbol.
- For instance, in a vending machine, the transducer would consider the current state (e.g. the amount of money inserted) as well as the input (e.g. the selected item) to produce an output (e.g. dispensing the item).
In conclusion, a transducer is an automaton that considers both the current input and previous states to generate an output. It plays a crucial role in various applications where complex behavior based on history and current input is required.
Given Language L= {xϵ {a, b}*|x contains aba as its substring}Find the difference of transitions made in constructing a DFA and an equivalent NFA?- a)2
- b)3
- c)4
- d)Cannot be determined.
Correct answer is option 'A'. Can you explain this answer?
Given Language L= {xϵ {a, b}*|x contains aba as its substring}Find the difference of transitions made in constructing a DFA and an equivalent NFA?
a)
2
b)
3
c)
4
d)
Cannot be determined.
|
|
Aravind Sengupta answered |
The individual Transition graphs can be made and the difference of transitions can be determined.
The number of elements in the set for the Language L={xϵ(∑r) *|length if x is at most 2} and ∑={0,1} is_________- a)7
- b)6
- c)8
- d)5
Correct answer is option 'A'. Can you explain this answer?
The number of elements in the set for the Language L={xϵ(∑r) *|length if x is at most 2} and ∑={0,1} is_________
a)
7
b)
6
c)
8
d)
5
|
|
Subhankar Shah answered |
∑r= {1,0} and a Kleene* operation would lead to the following set=COUNT{ε,0,1,00,11,01,10} =7.
Which among the following is not notated as infinite language?- a)Palindrome
- b)Reverse
- c)Factorial
- d)L={ab}*
Correct answer is option 'C'. Can you explain this answer?
Which among the following is not notated as infinite language?
a)
Palindrome
b)
Reverse
c)
Factorial
d)
L={ab}*
|
|
Bijoy Sharma answered |
Factorial, here is the most appropriate non-infinite domain. Otherwise, palindrome and reverse have infinite domains.
Which of the following is correct proposition?
Statement 1: Non determinism is a generalization of Determinism.
Statement 2: Every DFA is automatically an NFA- a)Statement 1 is correct because Statement 2 is correct
- b)Statement 2 is correct because Statement 2 is correct
- c)Statement 2 is false and Statement 1 is false
- d)Statement 1 is false because Statement 2 is false
Correct answer is option 'B'. Can you explain this answer?
Which of the following is correct proposition?
Statement 1: Non determinism is a generalization of Determinism.
Statement 2: Every DFA is automatically an NFA
Statement 1: Non determinism is a generalization of Determinism.
Statement 2: Every DFA is automatically an NFA
a)
Statement 1 is correct because Statement 2 is correct
b)
Statement 2 is correct because Statement 2 is correct
c)
Statement 2 is false and Statement 1 is false
d)
Statement 1 is false because Statement 2 is false
|
|
Raksha Mishra answered |
DFA is a specific case of NFA.
Given:
L= {xϵ∑= {0,1} |x=0n1n for n>=1}; Can there be a DFA possible for the language?- a)Yes
- b)No
Correct answer is option 'B'. Can you explain this answer?
Given:
L= {xϵ∑= {0,1} |x=0n1n for n>=1}; Can there be a DFA possible for the language?
L= {xϵ∑= {0,1} |x=0n1n for n>=1}; Can there be a DFA possible for the language?
a)
Yes
b)
No
|
|
Kunal Gupta answered |
It is not possible to have a count of equal number of 0 and 1 at any instant in DFA. Thus, It is not possible to build a DFA for the given Language.
Given Language: L= {xϵ∑= {a, b} |x has a substring ‘aa’ in the production}. Which of the corresponding representation notate the same?- a)

- b)

- c)

- d)

Correct answer is option 'A'. Can you explain this answer?
Given Language: L= {xϵ∑= {a, b} |x has a substring ‘aa’ in the production}. Which of the corresponding representation notate the same?
a)
b)
c)
d)
|
|
Nilanjan Chavan answered |
The states transited has been written corresponding to the transitions as per the row and column. The row represents the transitions made and the ultimate.
Which of the following does not belong to input alphabet if S={a, b}* for any language?- a)a
- b)b
- c)e
- d)none of the mentioned
Correct answer is option 'C'. Can you explain this answer?
Which of the following does not belong to input alphabet if S={a, b}* for any language?
a)
a
b)
b
c)
e
d)
none of the mentioned
|
|
Hrishikesh Saini answered |
The automaton may be allowed to change its state without reading the input symbol using epsilon but this does not mean that epsilon has become an input symbol. On the contrary, one assumes that the symbol epsilon does not belong to any alphabet.
Which of the following is not an example of finite state machine system?- a)Control Mechanism of an elevator
- b)Combinational Locks
- c)Traffic Lights
- d)Digital Watches
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not an example of finite state machine system?
a)
Control Mechanism of an elevator
b)
Combinational Locks
c)
Traffic Lights
d)
Digital Watches
|
|
Akshay Singh answered |
Proper and sequential combination of events leads the machines to work in hand which includes The elevator, Combinational Locks, Traffic Lights, vending machine, etc. Other applications of Finite machine state system are Communication Protocol Design, Artificial Intelligence Research, A Turnstile, etc.
Hence Option (D) is correct
For chapter notes on Finite Automata click on the following link:
Which of the following is a regular language?- a)String whose length is a sequence of prime numbers
- b)String with substring wwr in between
- c)Palindrome string
- d)String with even number of Zero’s
Correct answer is option 'D'. Can you explain this answer?
Which of the following is a regular language?
a)
String whose length is a sequence of prime numbers
b)
String with substring wwr in between
c)
Palindrome string
d)
String with even number of Zero’s
|
|
Sankar Sarkar answered |
DFSM’s for the first three option is not possible; hence they aren’t regular.
A Language for which no DFA exist is a________- a)Regular Language
- b)Non-Regular Language
- c)May be Regular
- d)Cannot be said
Correct answer is option 'B'. Can you explain this answer?
A Language for which no DFA exist is a________
a)
Regular Language
b)
Non-Regular Language
c)
May be Regular
d)
Cannot be said
|
|
Dhruba Goyal answered |
A language for which there is no existence of a deterministic finite automata is always Non Regular and methods like Pumping Lemma can be used to prove the same.
For a DFA accepting binary numbers whose decimal equivalent is divisible by 4, what are all the possible remainders?- a)0
- b)0,2
- c)0,2,4
- d)0,1,2,3
Correct answer is option 'D'. Can you explain this answer?
For a DFA accepting binary numbers whose decimal equivalent is divisible by 4, what are all the possible remainders?
a)
0
b)
0,2
c)
0,2,4
d)
0,1,2,3
|
|
Anisha Ahuja answered |
All the decimal numbers on division would lead to only 4 remainders i.e. 0,1,2,3 (Property of Decimal division).
Let the given DFA consist of x states. Find x-y such that y is the number of states on minimization of DFA?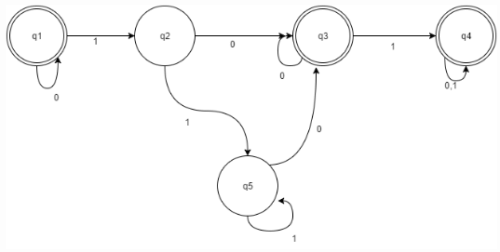
- a)3
- b)2
- c)1
- d)4
Correct answer is option 'B'. Can you explain this answer?
Let the given DFA consist of x states. Find x-y such that y is the number of states on minimization of DFA?
a)
3
b)
2
c)
1
d)
4
|
|
Gauri Banerjee answered |
Use the equivalence theorem or Myphill Nerode theorem to minimize the DFA
Given Language: L= {ab U aba}*If X is the minimum number of states for a DFA and Y is the number of states to construct the NFA,|X-Y|=?- a)2
- b)3
- c)4
- d)1
Correct answer is option 'A'. Can you explain this answer?
Given Language: L= {ab U aba}*If X is the minimum number of states for a DFA and Y is the number of states to construct the NFA,|X-Y|=?
a)
2
b)
3
c)
4
d)
1
|
|
Priyanka Chopra answered |
Construct the DFA and NFA individually, and attain the difference of states.
NFA, in its name has ’non-deterministic’ because of :- a)The result is undetermined
- b)The choice of path is non-deterministic
- c)The state to be transited next is non-deterministic
- d)All of the mentioned
Correct answer is option 'B'. Can you explain this answer?
NFA, in its name has ’non-deterministic’ because of :
a)
The result is undetermined
b)
The choice of path is non-deterministic
c)
The state to be transited next is non-deterministic
d)
All of the mentioned
|
|
Parth Sen answered |
Non deterministic or deterministic depends upon the definite path defined for the transition from one state to another or undefined(multiple paths).
A binary string is divisible by 4 if and only if it ends with:- a)100
- b)1000
- c)1100
- d)0011
Correct answer is option 'A'. Can you explain this answer?
A binary string is divisible by 4 if and only if it ends with:
a)
100
b)
1000
c)
1100
d)
0011
|
|
Tanishq Chavan answered |
Explanation:
In order to understand why a binary string is divisible by 4 if and only if it ends with "100", we need to understand what it means for a number to be divisible by 4 in binary.
Binary division rule:
Now, let's consider the binary numbers that end with "100". In order to determine if they are divisible by 4, we need to look at their last two digits.
Examples:
As we can see from the examples, any binary number that ends with "100" has the last two digits as "00", which means it is divisible by 4. Therefore, the correct answer is option "A".
In order to understand why a binary string is divisible by 4 if and only if it ends with "100", we need to understand what it means for a number to be divisible by 4 in binary.
Binary division rule:
- A binary number is divisible by 4 if and only if the last two digits are "00".
Now, let's consider the binary numbers that end with "100". In order to determine if they are divisible by 4, we need to look at their last two digits.
Examples:
- 1100 - The last two digits are "00", so this number is divisible by 4.
- 10100 - The last two digits are "00", so this number is divisible by 4.
- 11100 - The last two digits are "00", so this number is divisible by 4.
As we can see from the examples, any binary number that ends with "100" has the last two digits as "00", which means it is divisible by 4. Therefore, the correct answer is option "A".
A ___________ is a substitution such that h(a) contains a string for each a.- a)Closure
- b)Interchange
- c)Homomorphism
- d)Inverse Homomorphism
Correct answer is option 'C'. Can you explain this answer?
A ___________ is a substitution such that h(a) contains a string for each a.
a)
Closure
b)
Interchange
c)
Homomorphism
d)
Inverse Homomorphism
|
|
Tanishq Chakraborty answered |
Homomorphism Explanation:
Homomorphism is a concept in mathematics and computer science that refers to a structure-preserving map between two algebraic structures. In the context of formal languages and automata theory, a homomorphism is a substitution that maps symbols from one alphabet to strings of symbols in another alphabet. Here's an explanation of why option 'C' is the correct answer:
Definition of Homomorphism:
- A homomorphism h from an alphabet Σ to an alphabet Γ is a function that maps symbols from Σ to strings of symbols in Γ, i.e., h: Σ → Γ*.
- For each symbol a in Σ, h(a) is a string in Γ*.
Example:
- Let's consider an example where Σ = {0, 1} and Γ = {a, b}.
- A homomorphism h can be defined as h(0) = a, h(1) = b.
- Using this homomorphism, the string "0101" in Σ can be mapped to the string "abab" in Γ.
Application in Formal Languages:
- In formal languages, homomorphisms are used to define transformations between languages.
- For example, a homomorphism can be used to define a transformation between regular languages by mapping symbols from one language to strings of symbols in another language.
Conclusion:
- In the given context of a substitution where h(a) contains a string for each symbol a, the correct option is a homomorphism (option 'C'). This is because a homomorphism precisely defines such a substitution mapping symbols to strings in another alphabet.
Is the language preserved in all the steps while eliminating epsilon transitions from a NFA?- a)yes
- b)no
Correct answer is option 'A'. Can you explain this answer?
Is the language preserved in all the steps while eliminating epsilon transitions from a NFA?
a)
yes
b)
no
|
|
Harshitha Banerjee answered |
Yes, the language is preserved during the dteps of construction: L(N)=L(N1)=L(N2)=L(3).
Complement of a DFA can be obtained by- a)making starting state as final state.
- b)no trival method.
- c)making final states non-final and non-final to final.
- d)make final as a starting state.
Correct answer is option 'C'. Can you explain this answer?
Complement of a DFA can be obtained by
a)
making starting state as final state.
b)
no trival method.
c)
making final states non-final and non-final to final.
d)
make final as a starting state.
|
|
Ashutosh Pillai answered |
String accepted in previous DFA will not be accepted and non accepting string will be accepted .
Chapter doubts & questions for Regular Expressions, Languages, Grammar & Finite Automata - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Regular Expressions, Languages, Grammar & Finite Automata - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
453 videos|1305 docs|700 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup










