All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Discrete Mathematics for Computer Science Engineering (CSE) Exam
A fair coin is tossed 10 times. What is the probability that ONLY the first two tosses will yield heads? - a)
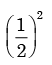
- b)
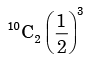
- c)
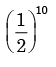
- d)
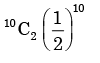
Correct answer is option 'C'. Can you explain this answer?
A fair coin is tossed 10 times. What is the probability that ONLY the first two tosses will yield heads?
a)
b)
c)
d)
|
|
Rhea Reddy answered |
Let A be the event that first toss is head
And B be the event that second toss is head.
By the given condition rest all 8 tosses should be tail
∴ The probability of getting head in first two cases
The 12 houses on one side of a street are numbered with even numbers starting at 2 and going up to 24. A free newspaper is delivered on Monday to 3 different houses chosen at random from these 12. Find the probability that at least 2 of these newspapers are delivered to houses with numbers strictly greater than 14.- a)7/11
- b)5/12
- c)4/11
- d)5/22
Correct answer is option 'C'. Can you explain this answer?
The 12 houses on one side of a street are numbered with even numbers starting at 2 and going up to 24. A free newspaper is delivered on Monday to 3 different houses chosen at random from these 12. Find the probability that at least 2 of these newspapers are delivered to houses with numbers strictly greater than 14.
a)
7/11
b)
5/12
c)
4/11
d)
5/22
|
|
Ravi Singh answered |
There are 12 houses on one side of a street are numbered with even numbers.
In which 5 houses are strictly greater than Number 14.
And remaining 7 houses are numbered smaller than 14 (i.e. including 14)
No of way of choosing at least 2 of these newspapers are delivered to houses with numbers strictly greater than 14.
5C3 +5C2 * 7C1 =80
Total way of choosing 3 houses=12C3 =220
So Required probability=80/220=4/11
In which 5 houses are strictly greater than Number 14.
And remaining 7 houses are numbered smaller than 14 (i.e. including 14)
No of way of choosing at least 2 of these newspapers are delivered to houses with numbers strictly greater than 14.
5C3 +5C2 * 7C1 =80
Total way of choosing 3 houses=12C3 =220
So Required probability=80/220=4/11
Suppose p is the number of cars per minute passing through a certain road junction between 5 PM and 6 PM, and p has a Poisson distribution with mean 3. What is the probability of observing fewer than 3 cars during any given minute in this interval?- a)
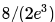
- b)
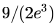
- c)
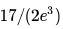
- d)
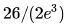
Correct answer is option 'C'. Can you explain this answer?
Suppose p is the number of cars per minute passing through a certain road junction between 5 PM and 6 PM, and p has a Poisson distribution with mean 3. What is the probability of observing fewer than 3 cars during any given minute in this interval?
a)
b)
c)
d)
|
|
Sanya Agarwal answered |
Poisson Probability Density Function (with mean 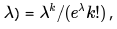
We have to sum the probability density function for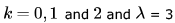 (thus finding the cumulative mass function)
(thus finding the cumulative mass function)
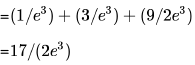
We have to sum the probability density function for
Suppose a fair six-sided die is rolled once. If the value on the die is 1, 2, or 3, the die is rolled a second time. What is the probability that the sum total of values that turn up is at least 6?- a)10/21
- b)5/12
- c)2/3
- d)1/6
Correct answer is option 'B'. Can you explain this answer?
Suppose a fair six-sided die is rolled once. If the value on the die is 1, 2, or 3, the die is rolled a second time. What is the probability that the sum total of values that turn up is at least 6?
a)
10/21
b)
5/12
c)
2/3
d)
1/6

|
Cstoppers Instructors answered |
Here our sample space consists of 3 + 3 * 6 = 21 events- (4), (5), (6), (1,1), (1,2) ... (3,6).
Favorable cases = (6), (1,5), (1,6), (2, 4), (2, 5), (2, 6), (3, 3), (3,4), (3,5), (3,6)
Required Probability = No. of favorable cases/Total cases = 10/21
But this is wrong way of doing. Because due to 2 tosses for some and 1 for some, individual probabilities are not the same. i.e., while (6) has 1/6 probability of occurrence, (1,5) has only 1/36 probability. So, our required probability
= 1/6 + (9 * 1/36) = 5/12
Favorable cases = (6), (1,5), (1,6), (2, 4), (2, 5), (2, 6), (3, 3), (3,4), (3,5), (3,6)
Required Probability = No. of favorable cases/Total cases = 10/21
But this is wrong way of doing. Because due to 2 tosses for some and 1 for some, individual probabilities are not the same. i.e., while (6) has 1/6 probability of occurrence, (1,5) has only 1/36 probability. So, our required probability
= 1/6 + (9 * 1/36) = 5/12
An examination paper has 150 multiple choice questions of one mark each, with each question having four choices. Each incorrect answer fetches -0.25 marks. Suppose 1000 students choose all their answers randomly with uniform probability.The sum total of the expected marks obtained by all these students is- a)0
- b)2550
- c)7525
- d)9375
Correct answer is option 'D'. Can you explain this answer?
An examination paper has 150 multiple choice questions of one mark each, with each question having four choices. Each incorrect answer fetches -0.25 marks. Suppose 1000 students choose all their answers randomly with uniform probability.The sum total of the expected marks obtained by all these students is
a)
0
b)
2550
c)
7525
d)
9375

|
EduRev GATE answered |
Probability of choosing the correct option = 1/4
Probability of choosing a wrong option = 1/3
So, expected mark for a question for a student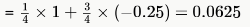
Expected mark for a student for 150 questions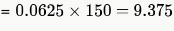
So, sum total of the expected marks obtained by all 1000 students
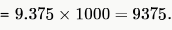
Probability of choosing a wrong option = 1/3
So, expected mark for a question for a student
Expected mark for a student for 150 questions
So, sum total of the expected marks obtained by all 1000 students
F is an n*n real matrix. b is an n*1 real vector. Suppose there are two n*1 vectors, u and v such that, u ≠ v and Fu = b, Fv = b. Which one of the following statements is false?- a)Determinant of F is zero.
- b)There are an infinite number of solutions to Fx = b
- c)There is an x≠0 such that Fx = 0
- d)F must have two identical rows
Correct answer is option 'D'. Can you explain this answer?
F is an n*n real matrix. b is an n*1 real vector. Suppose there are two n*1 vectors, u and v such that, u ≠ v and Fu = b, Fv = b. Which one of the following statements is false?
a)
Determinant of F is zero.
b)
There are an infinite number of solutions to Fx = b
c)
There is an x≠0 such that Fx = 0
d)
F must have two identical rows
|
|
Ravi Singh answered |
(A) : Correct. We are given
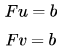
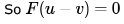
Since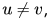 so we have a non-zero solution
so we have a non-zero solution  to homogeneous equation
to homogeneous equation 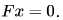 Now any vector
Now any vector 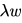 is also a solution of
is also a solution of  and so we have infinitely many solutions of
and so we have infinitely many solutions of  and so determinant of F is zero.
and so determinant of F is zero.
(B) : Correct. Consider a vector
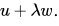
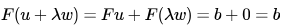
So there are infinitely many vectors of the form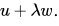 which are solutions to equation Fx = b.
which are solutions to equation Fx = b.
(C) : Correct. In option (a), we proved that vector
(D) : False. This is not necessary.
So option (D) is the answer.
Since
(B) : Correct. Consider a vector
So there are infinitely many vectors of the form
(C) : Correct. In option (a), we proved that vector
(D) : False. This is not necessary.
So option (D) is the answer.
The larger of the two eigenvalues of the matrix 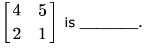
Correct answer is '6'. Can you explain this answer?
The larger of the two eigenvalues of the matrix 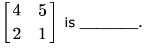

|
Gate Gurus answered |
For finding the Eigen Values of a Matrix we need to build the Characteristic equation which is of the form,
A - λI
Where A is the given Matrix.
λ is a constant
Where A is the given Matrix.
λ is a constant
I is the identity matrix.
We'll have a Linear equation after solving A - λI. Which will give us 2 roots for λ.
We'll have a Linear equation after solving A - λI. Which will give us 2 roots for λ.
6 is larger and hence is the Answer.
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering? 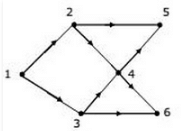
- a)1 2 3 4 5 6
- b)1 3 2 4 5 6
- c)1 3 2 4 6 5
- d)3 2 4 1 6 5
Correct answer is option 'D'. Can you explain this answer?
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?
a)
1 2 3 4 5 6
b)
1 3 2 4 5 6
c)
1 3 2 4 6 5
d)
3 2 4 1 6 5
|
|
Ravi Singh answered |
In option D, 1 appears after 2 and 3 which is not possible in Topological Sorting. In the given DAG it is directly visible that there is an outgoing edge from vertex 1 to vertex 2 and 3 hence 2 and 3 cannot come before vertex 1 so clearly option D is incorrect topological sort. But for questions in which it is not directly visible we should know how to find topological sort of a DAG.
Can you explain the answer of this question below:What is the logical translation of the following statement?
"None of my friends are perfect."
- A:

- B:
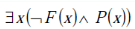
- C:
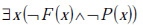
- D:
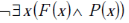
The answer is d.
What is the logical translation of the following statement?
"None of my friends are perfect."
|
|
Aditya Deshmukh answered |
F(x) ==> x is my friend
P(x) ==> x is perfect
D is the correct answer.
A. There exist some friends which are not perfect
B. There are some people who are not my friend and are perfect
C. There exist some people who are not my friend and are not perfect.
D. There doesn't exist any person who is my friend and perfect
A fair dice is rolled twice. The probability that an odd number will follow an even number is - a)1/2
- b)1/6
- c)1/3
- d)1/4
Correct answer is option 'D'. Can you explain this answer?
A fair dice is rolled twice. The probability that an odd number will follow an even number is
a)
1/2
b)
1/6
c)
1/3
d)
1/4

|
Raghavendra Sharma answered |
Probability of even number =3/6 =1/2
Probability of odd number =3/6 =1/2
Both are independent so probability=1/2.1/2 =1/4
A club with x members is organized into tour committees such that(a) each member is in exactly two committees,
(b) any two committees have exactly one member in common.Then x has- a)exactly two values both between 4 and 8
- b)exactly one value and this lies between 4 and 8
- c)exactly two values both between 8 and 16
- d)exactly one value and this lies between 8 and 16.
Correct answer is option 'B'. Can you explain this answer?
A club with x members is organized into tour committees such that
(a) each member is in exactly two committees,
(b) any two committees have exactly one member in common.
(b) any two committees have exactly one member in common.
Then x has
a)
exactly two values both between 4 and 8
b)
exactly one value and this lies between 4 and 8
c)
exactly two values both between 8 and 16
d)
exactly one value and this lies between 8 and 16.
|
|
Ravi Singh answered |
How many sub strings of different lengths (non-zero) can be found formed from a character string of length n ?- a)n
- b)n2
- c)2n
- d)
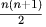
Correct answer is option 'D'. Can you explain this answer?
How many sub strings of different lengths (non-zero) can be found formed from a character string of length n ?
a)
n
b)
n2
c)
2n
d)
|
|
Yash Patel answered |
assuming an string of length n provided all alphabets are distinct..
no of strings of length 1 = n
no of strings of length 2 = n-1
no of strings of length 3 = n-2 .
.
.
no of string of length n = 1
total = n + (n -1) + (n - 2) + (n - 2) + ..... + 1
no of strings of length 1 = n
no of strings of length 2 = n-1
no of strings of length 3 = n-2 .
.
.
no of string of length n = 1
total = n + (n -1) + (n - 2) + (n - 2) + ..... + 1
= n(n+1)/2
The following is the Hasse diagram of the poset [{a, b, c, d, e}, ≤]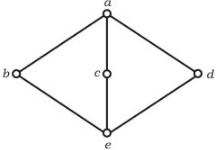 The poset is
The poset is- a)not a lattice
- b)a lattice but not a distributive lattice
- c)a distributive lattice but not a Boolean algebra
- d)a Boolean algebra
Correct answer is option 'B'. Can you explain this answer?
The following is the Hasse diagram of the poset [{a, b, c, d, e}, ≤]
The poset is
a)
not a lattice
b)
a lattice but not a distributive lattice
c)
a distributive lattice but not a Boolean algebra
d)
a Boolean algebra
|
|
Ravi Singh answered |
It is a lattice but not a distributive lattice.
Table for Join Operation of above Hesse diagram
Table for Meet Operation of above Hesse diagram
Therefore for any two element p, q in the lattice (A,<=) p <= p V q ; p^q <= p This satisfies for all element (a,b,c,d,e).
which has 'a' as unique least upper bound and 'e' as unique greatest lower bound.
The given lattice doesn't obey distributive law, so it is not distributive lattice,
which has 'a' as unique least upper bound and 'e' as unique greatest lower bound.
The given lattice doesn't obey distributive law, so it is not distributive lattice,
Note that for b,c,d we have distributive law
b^(cVd) = (b^c) V (b^d). From the diagram / tables given above we can verify as follows,
(i) L.H.S. = b ^ (c V d) = b ^ a = b
(ii) R.H.S. = (b^c) V (b^d) = e v e = e
b != e which contradict the distributive law. Hence it is not distributive lattice. so, option (B) is correct.
b^(cVd) = (b^c) V (b^d). From the diagram / tables given above we can verify as follows,
(i) L.H.S. = b ^ (c V d) = b ^ a = b
(ii) R.H.S. = (b^c) V (b^d) = e v e = e
b != e which contradict the distributive law. Hence it is not distributive lattice. so, option (B) is correct.
An examination consists of two papers, Paper 1 and Paper 2. The probability of failing in Paper 1 is 0.3 and that in Paper 2 is 0.2. Given that a student has failed in Paper 2, the probability of failing in Paper 1 is 0.6. The probability of a student failing in both the papers is- a)0.5
- b)0.18
- c) 0.12
- d) 0.06
Correct answer is option 'C'. Can you explain this answer?
An examination consists of two papers, Paper 1 and Paper 2. The probability of failing in Paper 1 is 0.3 and that in Paper 2 is 0.2. Given that a student has failed in Paper 2, the probability of failing in Paper 1 is 0.6. The probability of a student failing in both the papers is
a)
0.5
b)
0.18
c)
0.12
d)
0.06

|
Tanu Shindekar answered |
The probability of a student failing in both papers is 0.12
The minimum number of colours required to colour the following graph, such that no two adjacent vertices are assigned the same colour, is
- a)2
- b)3
- c)4
- d)5
Correct answer is option 'C'. Can you explain this answer?
The minimum number of colours required to colour the following graph, such that no two adjacent vertices are assigned the same colour, is
a)
2
b)
3
c)
4
d)
5
|
|
Yash Patel answered |
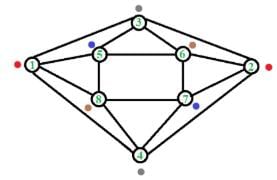
Two vertices are said to be adjacent if they are directly connected, i.e., there is a direct edge between them. So, here, we can assign same color to 1 & 2 (red), 3 & 4 (grey), 5 & 7 (blue) and 6 & 8 (brown). Therefore, we need a total of 4 distinct colors. Thus, C is the correct choice.
Please comment below if you find anything wrong in the above post.
If matrix 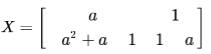 and X2 - X + I = 0 (I is the identity matrix and is the zero matrix), then the inverse of X is
and X2 - X + I = 0 (I is the identity matrix and is the zero matrix), then the inverse of X is- a)
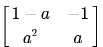
- b)
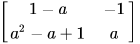
- c)
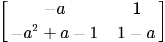
- d)
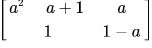
Correct answer is option 'B'. Can you explain this answer?
If matrix 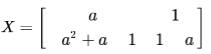 and X2 - X + I = 0 (I is the identity matrix and is the zero matrix), then the inverse of X is
and X2 - X + I = 0 (I is the identity matrix and is the zero matrix), then the inverse of X is
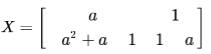 and X2 - X + I = 0 (I is the identity matrix and is the zero matrix), then the inverse of X is
and X2 - X + I = 0 (I is the identity matrix and is the zero matrix), then the inverse of X isa)
b)
c)
d)
|
|
Yash Patel answered |
Given, X2 - X + I = O
=> X2 = X - I
=> X-1 (X2) = X-1(X - I) {Multiplying X-1 both sides..}
=> X = I - X-1
=> X-1 = I - X
=> X2 = X - I
=> X-1 (X2) = X-1(X - I) {Multiplying X-1 both sides..}
=> X = I - X-1
=> X-1 = I - X
Which gives Option (B)..
We need to choose a team of 11 from a pool of 15 players and also select a captain. The number of different ways this can be done is- a)
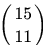
- b)
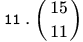
- c)15 . 14 . 13 . 12 . 11 .10 . 9 . 8 . 7 . 6 . 5
- d)(15 . 14 . 13 . 12 . 11 .10 . 9 . 8 . 7 . 6 . 5) . 11
Correct answer is option 'B'. Can you explain this answer?
We need to choose a team of 11 from a pool of 15 players and also select a captain. The number of different ways this can be done is
a)
b)
c)
15 . 14 . 13 . 12 . 11 .10 . 9 . 8 . 7 . 6 . 5
d)
(15 . 14 . 13 . 12 . 11 .10 . 9 . 8 . 7 . 6 . 5) . 11
|
|
Ajit Kumar answered |
11 players can be selected in 15C11 ways and then the captain can be selected in 11 ways. so total numbers of ways is 11*15C11
Which of the following is TRUE about formulae in Conjunctive Normal Form?- a)For any formula, there is a truth assignment for which at least half the clauses evaluate to true.
- b)For any formula, there is a truth assignment for which all the clauses evaluate to true
- c)There is a formula such that for each truth assignment, at most one-fourth of the clauses evaluate to true.
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
Which of the following is TRUE about formulae in Conjunctive Normal Form?
a)
For any formula, there is a truth assignment for which at least half the clauses evaluate to true.
b)
For any formula, there is a truth assignment for which all the clauses evaluate to true
c)
There is a formula such that for each truth assignment, at most one-fourth of the clauses evaluate to true.
d)
None of the above

|
Rounak Choudhary answered |
We can easily prove that for any formula, there is a truth assignment for which at least half the clauses evaluate to true . Proof : Consider an arbitrary truth assignment. For each of its clause ‘j’ , introduce a random variable. Xj = 1 if clause ‘j’ is satisfied Xj = 0 otherwise Then, X = summation of (j * Xj) is the number of satisfied clauses. Given any clause ’c’ , it is unsatisfied only if all of its ‘k’ constituent literals evaluates to false as they are joined by OR operator. Now, because each literal within a clause has a 1/2 chance of evaluating to true independently of any of the truth value of any of the other literals, the probability that they are all false is (1 / 2)k . Thus, the probability that ‘c’ is satisfied = 1 − (1 / 2)k So, E(Xj) = 1 * (1 / 2)k = (1 / 2)k Therefore, E(Xj) >= 1/2 Summation on both sides to get E(X). Therefore, we have E(X) = summation of (j * Xj) >= m/2 where ‘m’ is the number of clauses. E(X) represents expected number of satisfied clauses. Thus, there must exist an assignment that satisfies at least half of the clauses. Please comment below if you find anything wrong in the above post.
Make is a utility that automatically builds executable programs and libraries from source code by reading files called makefiles which specify how to derive the target program. Which of the following standard graph algorithms is used by Make.- a)Strongly Connected Components
- b)Topological Sorting
- c)Breadth First Search
- d)Dijkstra's Shortest Path
Correct answer is option 'B'. Can you explain this answer?
Make is a utility that automatically builds executable programs and libraries from source code by reading files called makefiles which specify how to derive the target program. Which of the following standard graph algorithms is used by Make.
a)
Strongly Connected Components
b)
Topological Sorting
c)
Breadth First Search
d)
Dijkstra's Shortest Path
|
|
Tarun Saini answered |
Make can decide the order of building a software using topological sorting. Topological sorting produces the order considering all dependencies provide by makefile. See following for details. Topological Sorting
Consider the binary relation:
S = {(x, y) | y = x+1 and x, y ∈ {0, 1, 2, ...}}Q. The reflexive transitive closure of S is- a){(x, y) | y > x and x, y ∈ {0, 1, 2, ... }}
- b){(x, y) | y ≥ x and x, y ∈ {0, 1, 2, ... }}
- c){(x, y) | y < x and x, y ∈ {0, 1, 2, ... }}
- d){(x, y) | y ≤ x and x, y ∈ {0, 1, 2, ... }}
Correct answer is option 'B'. Can you explain this answer?
Consider the binary relation:
S = {(x, y) | y = x+1 and x, y ∈ {0, 1, 2, ...}}
S = {(x, y) | y = x+1 and x, y ∈ {0, 1, 2, ...}}
Q. The reflexive transitive closure of S is
a)
{(x, y) | y > x and x, y ∈ {0, 1, 2, ... }}
b)
{(x, y) | y ≥ x and x, y ∈ {0, 1, 2, ... }}
c)
{(x, y) | y < x and x, y ∈ {0, 1, 2, ... }}
d)
{(x, y) | y ≤ x and x, y ∈ {0, 1, 2, ... }}
|
|
Ravi Singh answered |
Reflexive closure of a relation R on set S is the smallest reflexive relation which contains R.
If S = {(0, 1), (1, 2)} , we make it reflexive by taking its union with set {(0, 0), (1, 1), (2, 2)}. Thus, reflexive closure of S = {(0, 0), (0, 1), (1, 1), (1, 2), (2, 2)}.
Now transitive closure is defined as smallest transitive relation which contains S.
We check where does it violate property of transitivity then add appropriate pair. We have (0, 1) and (1, 2) but not (0, 2). So, S = {(0, 0), (0, 1), (0, 2), (1, 1), (1, 2), (2, 2)} now.
Thus, option (B) matches the final set S.
Please comment below if you find anything wrong in the above post.
If S = {(0, 1), (1, 2)} , we make it reflexive by taking its union with set {(0, 0), (1, 1), (2, 2)}. Thus, reflexive closure of S = {(0, 0), (0, 1), (1, 1), (1, 2), (2, 2)}.
Now transitive closure is defined as smallest transitive relation which contains S.
We check where does it violate property of transitivity then add appropriate pair. We have (0, 1) and (1, 2) but not (0, 2). So, S = {(0, 0), (0, 1), (0, 2), (1, 1), (1, 2), (2, 2)} now.
Thus, option (B) matches the final set S.
Please comment below if you find anything wrong in the above post.
The matrices 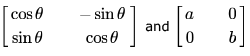 commute under multiplication
commute under multiplication- a)
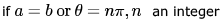
- b)always
- c)never
- d)
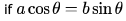
Correct answer is option 'A'. Can you explain this answer?
The matrices 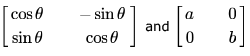 commute under multiplication
commute under multiplication
a)
b)
always
c)
never
d)
|
|
Yash Patel answered |
The multiplication will commute if
The number of binary strings of zeros and ones in which no two ones are adjacent is- a)n−1Ck
- b)nCk
- c)nCk+1
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
The number of binary strings of zeros and ones in which no two ones are adjacent is
a)
n−1Ck
b)
nCk
c)
nCk+1
d)
None of the above
|
|
Yash Patel answered |
first place n zeroes side by side _ 0 _ 0 _ 0 ... 0 _
k 1's can be placed in any of the (n+1) available gaps hence number of ways = n+1Ck
k 1's can be placed in any of the (n+1) available gaps hence number of ways = n+1Ck
A box contains 2 washers, 3 nuts and 4 bolts. Items are drawn from the box at random one at a time without replacement. The probability of drawing 2 washers first followed by 3 nuts and subsequently the 4 bolts is- a)2/315
- b)1/630
- c)1/1260
- d)1/2520
Correct answer is option 'C'. Can you explain this answer?
A box contains 2 washers, 3 nuts and 4 bolts. Items are drawn from the box at random one at a time without replacement. The probability of drawing 2 washers first followed by 3 nuts and subsequently the 4 bolts is
a)
2/315
b)
1/630
c)
1/1260
d)
1/2520
|
|
Jaideep Dasgupta answered |
Here sample space = 9
The required probability of drawing 2 washers, 3 nuts and 4 bolts respectively without replac ement
Consider the recurrence relation a1 = 8, an = 6n2 + 2n + an-1. Let a99 = K x 104 . The value of K is __________.- a)198 × 104
- b)194 × 104
- c)192 × 104
- d)196 × 104
Correct answer is option 'A'. Can you explain this answer?
Consider the recurrence relation a1 = 8, an = 6n2 + 2n + an-1. Let a99 = K x 104 . The value of K is __________.
a)
198 × 104
b)
194 × 104
c)
192 × 104
d)
196 × 104
|
|
Ravi Singh answered |
an = 6n2 + 2n + an−1
= 6n2 + 2n + 6(n − 1)2 + 2(n − 1) + an−2
= 6n2 + 2n + 6(n − 1)2 + 2(n − 1) + 6(n − 2)2 + 2(n − 2)+. . . . . . +a1
= 6n2 + 2n + 6(n − 1)2 + 2(n − 1) + 6(n − 2)2 + 2(n − 2)+. . . . . . +6.12 + 2.1
= 6(n2 + (n − 1)2 +. . . +22 + 12) + 2(n + (n − 1)+. . . +2 + 1)
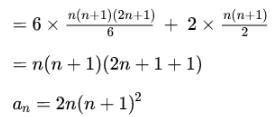 for n = 99 a99 = 2 x 99 x (99+1)2 = 198 x 104
for n = 99 a99 = 2 x 99 x (99+1)2 = 198 x 104
= 6n2 + 2n + 6(n − 1)2 + 2(n − 1) + an−2
= 6n2 + 2n + 6(n − 1)2 + 2(n − 1) + 6(n − 2)2 + 2(n − 2)+. . . . . . +a1
= 6n2 + 2n + 6(n − 1)2 + 2(n − 1) + 6(n − 2)2 + 2(n − 2)+. . . . . . +6.12 + 2.1
= 6(n2 + (n − 1)2 +. . . +22 + 12) + 2(n + (n − 1)+. . . +2 + 1)
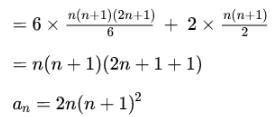 for n = 99 a99 = 2 x 99 x (99+1)2 = 198 x 104
for n = 99 a99 = 2 x 99 x (99+1)2 = 198 x 104In how many ways can three person, each throwing a single die once, make a score of 11- a)22
- b)27
- c)24
- d)38
Correct answer is option 'B'. Can you explain this answer?
In how many ways can three person, each throwing a single die once, make a score of 11
a)
22
b)
27
c)
24
d)
38
|
|
Akshay Singh answered |
The sum 11 can be broken as 6 + 5
Let us name the players as A, B and C.
Case 1: Fix 6 and break 5
Let us name the players as A, B and C.
Case 1: Fix 6 and break 5
Suppose A throws 6. Players B and C can throw dice in following four ways to make sum 5
(1,4), (2,3), (3,2) and (4,1)
As any of the three players can throw value 6, so there are total 3 x 4 = 12
(1,4), (2,3), (3,2) and (4,1)
As any of the three players can throw value 6, so there are total 3 x 4 = 12
Case 2: Fix 5 and break 6
Suppose A throws 5. Players B and C can throw dice in following five ways to make sum 6
(1,5), (2,4), (3,3), (4,2), (5,1)
As any of the three players can throw value 5, so there are total 3 x 5 = 15
Adding case 1 and case 2 there are total 12 + 15 = 27 ways
(1,5), (2,4), (3,3), (4,2), (5,1)
As any of the three players can throw value 5, so there are total 3 x 5 = 15
Adding case 1 and case 2 there are total 12 + 15 = 27 ways
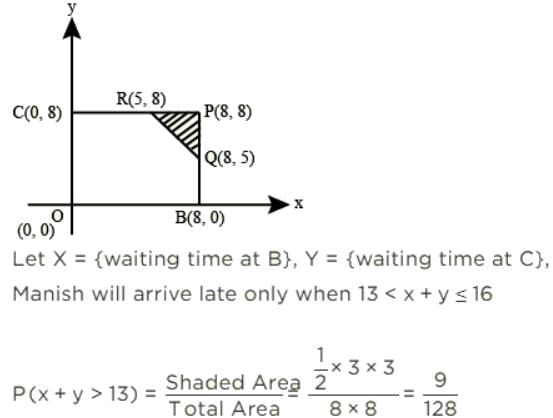
Manish has to travel from A to D changing buses at stops B and C enroute. The maximum waiting time at either stop can be 8 minutes each, but any time of waiting up to 8 minutes is equally likely at both places. He can afford up to 13 minutes of total waiting time if he is to arrive at D on time. What is the probability that Manish will arrive late at D?
- a)9/128
- b)13/64
- c)119/128
- d)8/13
Correct answer is option 'A'. Can you explain this answer?
Manish has to travel from A to D changing buses at stops B and C enroute. The maximum waiting time at either stop can be 8 minutes each, but any time of waiting up to 8 minutes is equally likely at both places. He can afford up to 13 minutes of total waiting time if he is to arrive at D on time. What is the probability that Manish will arrive late at D?
a)
9/128
b)
13/64
c)
119/128
d)
8/13

|
Machine Experts answered |
Which of the following statements is true for every planar graph on n vertices?- a)The graph is connected
- b)The graph is Eulerian
- c)The graph has a vertex-cover of size at most 3n/4
- d)The graph has an independent set of size at least n/3
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is true for every planar graph on n vertices?
a)
The graph is connected
b)
The graph is Eulerian
c)
The graph has a vertex-cover of size at most 3n/4
d)
The graph has an independent set of size at least n/3
|
|
Sanya Agarwal answered |
A planar graph is a graph which can drawn on a plan without any pair of edges crossing each other. A) FALSE: A disconnected graph can be planar as it can be drawn on a plane without crossing edges. B) FALSE: An Eulerian Graph may or may not be planar.An undirected graph is eulerian if all vertices have even degree. For example, the following graph is Eulerian, but not planar C) TRUE: D) FALSE:
Px(x) = M exp(–2|x|) – N exp(–3 |x|) is the probability density function for the real random variable X, over the entire x axis. M and N are both positive real numbers. The equation relating M and N is - a)
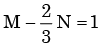
- b)
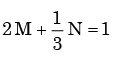
- c)

- d)
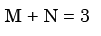
Correct answer is option 'A'. Can you explain this answer?
Px(x) = M exp(–2|x|) – N exp(–3 |x|) is the probability density function for the real random variable X, over the entire x axis. M and N are both positive real numbers. The equation relating M and N is
a)
b)
c)
d)

|
Pathways Academy answered |
Given Px (x ) is the probability density function for the random variable X.
What is the chromatic number of an n-vertex simple connected graph which does not contain any odd length cycle? Assume n >= 2.- a)2
- b)3
- c)n-1
- d)n
Correct answer is option 'A'. Can you explain this answer?
What is the chromatic number of an n-vertex simple connected graph which does not contain any odd length cycle? Assume n >= 2.
a)
2
b)
3
c)
n-1
d)
n
|
|
Sanaya Gupta answered |
The Chromatic Number of a Graph
The chromatic number of a graph is the minimum number of colors needed to color the vertices of the graph in such a way that no two adjacent vertices have the same color. In other words, it is the minimum number of colors needed to color the graph such that no two adjacent vertices have the same color.
Graphs Without Odd Length Cycles
An odd length cycle in a graph is a cycle (a path that starts and ends at the same vertex) with an odd number of edges. A graph that does not contain any odd length cycle is called bipartite. A bipartite graph is a graph whose vertices can be divided into two disjoint sets such that no two vertices within the same set are adjacent.
Chromatic Number of a Graph Without Odd Length Cycles
For a graph without any odd length cycle, it is always possible to color the vertices using only two colors. This is because we can divide the vertices into two sets, such that no two vertices within the same set are adjacent. Therefore, the chromatic number of the graph is 2.
Explanation
To understand why the chromatic number of a graph without any odd length cycle is 2, let's consider the following steps:
1. Assume that the graph has n vertices.
2. Since the graph is simple and connected, it must be a tree or a forest (a collection of disjoint trees).
3. If the graph is a tree, it is trivially bipartite, as we can color the vertices alternatively using two colors.
4. If the graph is a forest, we can still color the vertices using two colors. We can start with any vertex and assign it color 1. Then, for each adjacent vertex, assign it the opposite color. Continue this process until all vertices are colored.
5. Since the graph does not contain any odd length cycle, there will be no adjacent vertices with the same color, as the colors are assigned alternately.
6. Therefore, we have successfully colored the graph using only two colors.
7. Hence, the chromatic number of the graph is 2.
Conclusion
The chromatic number of an n-vertex simple connected graph which does not contain any odd length cycle is 2. This means that the graph can be colored using only two colors such that no two adjacent vertices have the same color.
The chromatic number of a graph is the minimum number of colors needed to color the vertices of the graph in such a way that no two adjacent vertices have the same color. In other words, it is the minimum number of colors needed to color the graph such that no two adjacent vertices have the same color.
Graphs Without Odd Length Cycles
An odd length cycle in a graph is a cycle (a path that starts and ends at the same vertex) with an odd number of edges. A graph that does not contain any odd length cycle is called bipartite. A bipartite graph is a graph whose vertices can be divided into two disjoint sets such that no two vertices within the same set are adjacent.
Chromatic Number of a Graph Without Odd Length Cycles
For a graph without any odd length cycle, it is always possible to color the vertices using only two colors. This is because we can divide the vertices into two sets, such that no two vertices within the same set are adjacent. Therefore, the chromatic number of the graph is 2.
Explanation
To understand why the chromatic number of a graph without any odd length cycle is 2, let's consider the following steps:
1. Assume that the graph has n vertices.
2. Since the graph is simple and connected, it must be a tree or a forest (a collection of disjoint trees).
3. If the graph is a tree, it is trivially bipartite, as we can color the vertices alternatively using two colors.
4. If the graph is a forest, we can still color the vertices using two colors. We can start with any vertex and assign it color 1. Then, for each adjacent vertex, assign it the opposite color. Continue this process until all vertices are colored.
5. Since the graph does not contain any odd length cycle, there will be no adjacent vertices with the same color, as the colors are assigned alternately.
6. Therefore, we have successfully colored the graph using only two colors.
7. Hence, the chromatic number of the graph is 2.
Conclusion
The chromatic number of an n-vertex simple connected graph which does not contain any odd length cycle is 2. This means that the graph can be colored using only two colors such that no two adjacent vertices have the same color.
Each of the nine words in the sentence " The quick brown fox jumps over the lazy dog" is written on a separate piece of paper. These nine pieces of paper are kept in a box. One of the pieces is drawn at random from the box. The length of the word drawn is _____________. (The answer should be rounded to one decimal place.)
Correct answer is '3.9'. Can you explain this answer?
Each of the nine words in the sentence " The quick brown fox jumps over the lazy dog" is written on a separate piece of paper. These nine pieces of paper are kept in a box. One of the pieces is drawn at random from the box. The length of the word drawn is _____________. (The answer should be rounded to one decimal place.)
|
|
Ravi Singh answered |
Each of the nine words have equal probability. So, expected length
Which one of the following is the most appropriate logical formula to represent the statement? "Gold and silver ornaments are precious". The following notations are used: G(x): x is a gold ornament S(x): x is a silver ornament P(x): x is precious- a)∀x(P(x)→(G(x)∧S(x)))
- b)∀x((G(x)∧S(x))→P(x))
- c)∃x((G(x)∧S(x))→P(x)
- d)∀x((G(x)∨S(x))→P(x))
Correct answer is option 'D'. Can you explain this answer?
Which one of the following is the most appropriate logical formula to represent the statement? "Gold and silver ornaments are precious". The following notations are used: G(x): x is a gold ornament S(x): x is a silver ornament P(x): x is precious
a)
∀x(P(x)→(G(x)∧S(x)))
b)
∀x((G(x)∧S(x))→P(x))
c)
∃x((G(x)∧S(x))→P(x)
d)
∀x((G(x)∨S(x))→P(x))

|
Anirban Khanna answered |
=> This statement can be expressed as
=> For all X, x can be either gold or silver then the ornament X is precious
=> For all X, (G(X) v S(x)) => P(X).
E1 and E2 are events in a probability space satisfying the following constraints: - Pr(E1) = Pr(E2)
- Pr(E1 ∪ E2) = 1
- E1 and E2 are independent
The value of Pr(E1), the probability of the event E1, is- a)0
- b)¼
- c)½
- d)1
Correct answer is option 'D'. Can you explain this answer?
E1 and E2 are events in a probability space satisfying the following constraints:
- Pr(E1) = Pr(E2)
- Pr(E1 ∪ E2) = 1
- E1 and E2 are independent
The value of Pr(E1), the probability of the event E1, is
a)
0
b)
¼
c)
½
d)
1
|
|
Yash Patel answered |
let probability of Event E1 = x = prob of E2
prob(E1 union E2) = prob(E1) + prob(E2) - prob(E1 intersect E2)
1 = x + x -x2 (prob(E1 intersect E2) = prob(E1) * prob(E2) as events are independent)
x = 1
prob(E1 union E2) = prob(E1) + prob(E2) - prob(E1 intersect E2)
1 = x + x -x2 (prob(E1 intersect E2) = prob(E1) * prob(E2) as events are independent)
x = 1
Let R1 be a relation from A = {1, 3, 5, 7} to B = {2, 4, 6, 8} and R2 be another relation from B to C = {1, 2, 3, 4} as defined below: - An element x in A is related to an element y in B (under R1) if x + y is divisible by 3.
- An element x in B is related to an element y in C (under R2) if x + y is even but not divisible by 3.
Q. Which is the composite relation R1R2 from A to C? - a)R1R2 = {(1, 2), (1, 4), (3, 3), (5, 4), (7, 3)}
- b)R1R2 = {(1, 2), (1, 3), (3, 2), (5, 2), (7, 3)}
- c)R1R2 = {(1, 2), (3, 2), (3, 4), (5, 4), (7, 2)}
- d)R1R2 = {(3, 2), (3, 4), (5, 1), (5, 3), (7, 1)}
Correct answer is option 'C'. Can you explain this answer?
Let R1 be a relation from A = {1, 3, 5, 7} to B = {2, 4, 6, 8} and R2 be another relation from B to C = {1, 2, 3, 4} as defined below:
- An element x in A is related to an element y in B (under R1) if x + y is divisible by 3.
- An element x in B is related to an element y in C (under R2) if x + y is even but not divisible by 3.
Q. Which is the composite relation R1R2 from A to C?
a)
R1R2 = {(1, 2), (1, 4), (3, 3), (5, 4), (7, 3)}
b)
R1R2 = {(1, 2), (1, 3), (3, 2), (5, 2), (7, 3)}
c)
R1R2 = {(1, 2), (3, 2), (3, 4), (5, 4), (7, 2)}
d)
R1R2 = {(3, 2), (3, 4), (5, 1), (5, 3), (7, 1)}
|
|
Yash Patel answered |
R1 is a relation from A = {1, 3, 5, 7} to B = {2, 4, 6, 8} . Under R1, an element x in A is related to an element y in B if x + y is divisible by 3.
Thus, R1 = {(1, 2), (1, 8), (3, 6), (5, 4), (7, 2), (7, 8)}
R2 is a relation from B = {2, 4, 6, 8} to C = {1, 2, 3, 4} Under R2, an element y in B is related to an element z in C if y + z is even but not divisible by 3.
Thus, R2 = {(2, 2), (4, 4), (6, 2), (6, 4), (8, 2)}
Thus, R1 = {(1, 2), (1, 8), (3, 6), (5, 4), (7, 2), (7, 8)}
R2 is a relation from B = {2, 4, 6, 8} to C = {1, 2, 3, 4} Under R2, an element y in B is related to an element z in C if y + z is even but not divisible by 3.
Thus, R2 = {(2, 2), (4, 4), (6, 2), (6, 4), (8, 2)}
Thus, R1R2 = {(1, 2), (3, 2), (3, 4), (5, 4), (7, 2)}
Thus, option (C) is correct.
Please comment below if you find anything wrong in the above post.
Thus, option (C) is correct.
Please comment below if you find anything wrong in the above post.
Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?- a)1/8
- b)1
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?
a)
1/8
b)
1
c)
7
d)
8
|
|
Rajeev Menon answered |
A cycle of length 3 can be formed with 3 vertices. There can be total 8C3 ways to pick 3 vertices from 8. The probability that there is an edge between two vertices is 1/2. So expected number of unordered cycles of length 3 = (8C3)*(1/2)^3 = 7
In questions 1.1 to 1.7 below, one or more of the alternatives are correct. Write the code letter(s) a, b, c, d corresponding to the correct alternative(s) in the answer book. Marks will be given only if all the correct alternatives have been selected and no incorrect alternative is picked up. 1.1). The eigen vector (s) of the matrix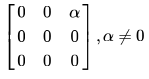 is (are)
is (are)- a)
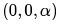
- b)
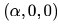
- c)
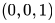
- d)
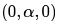
Correct answer is option 'B,D'. Can you explain this answer?
In questions 1.1 to 1.7 below, one or more of the alternatives are correct. Write the code letter(s) a, b, c, d corresponding to the correct alternative(s) in the answer book. Marks will be given only if all the correct alternatives have been selected and no incorrect alternative is picked up. 1.1). The eigen vector (s) of the matrix
is (are)
a)
b)
c)
d)
|
|
Ravi Singh answered |
Eigen values are: 0,0,0
The eigen vector should satisfy the equation: αz = 0
The eigen vector should satisfy the equation: αz = 0
A probability density function is of the form 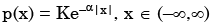 The value of K is
The value of K is - a)0.5
- b)1
- c)0.5α
- d)α
Correct answer is option 'C'. Can you explain this answer?
A probability density function is of the form
The value of K is
a)
0.5
b)
1
c)
0.5α
d)
α
|
|
Ravi Singh answered |
As (x) is a probability density function
Seven (distinct) car accidents occurred in a week. What is the probability that they all occurred on the same day?- a)
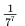
- b)
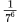
- c)
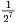
- d)
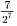
Correct answer is option 'B'. Can you explain this answer?
Seven (distinct) car accidents occurred in a week. What is the probability that they all occurred on the same day?
a)
b)
c)
d)
|
|
Yash Patel answered |
for every car accident we can pick a day in 7 ways
total number of ways in which accidents can be assigned to days = 77
probability of accidents happening on a particular day = 1/77
we can choose a day in 7 ways
hence probability = 7/77= 1/76
total number of ways in which accidents can be assigned to days = 77
probability of accidents happening on a particular day = 1/77
we can choose a day in 7 ways
hence probability = 7/77= 1/76
Compute the value of: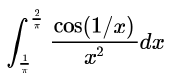
Correct answer is '-1'. Can you explain this answer?
Compute the value of:

|
Naroj Boda answered |
For the integrand
This gives a new lower bound
Since the antiderivative of cos(u) is sin (u) , applying the fundamental theorem of calculus, we get:
Box P has 2 red balls and 3 blue balls and box Q has 3 red balls and 1 blue ball. A ball is selected as follows:(i) select a box
(ii) choose a ball from the selected box such that each ball in the box is equally likely to be chosen. The probabilities of selecting boxes P and Q are 1/3 and 2/3 respectively. Given that a ball selected in the above process is a red ball, the probability that it came from the box P is:- a)4/19
- b)5/19
- c)2/9
- d)19/30
Correct answer is option 'A'. Can you explain this answer?
Box P has 2 red balls and 3 blue balls and box Q has 3 red balls and 1 blue ball. A ball is selected as follows:
(i) select a box
(ii) choose a ball from the selected box such that each ball in the box is equally likely to be chosen. The probabilities of selecting boxes P and Q are 1/3 and 2/3 respectively. Given that a ball selected in the above process is a red ball, the probability that it came from the box P is:
(ii) choose a ball from the selected box such that each ball in the box is equally likely to be chosen. The probabilities of selecting boxes P and Q are 1/3 and 2/3 respectively. Given that a ball selected in the above process is a red ball, the probability that it came from the box P is:
a)
4/19
b)
5/19
c)
2/9
d)
19/30
|
|
Ravi Singh answered |
The probability of selecting a red ball = (1/3) * (2/5) + (2/3) * (3/4) = 2/15 + 1/2
= 19/30
Probability of selecting a red ball from box P = (1/3) * (2/5) = 2/15
Given that a ball selected in the above process is a red ball, the probability that it came from the box P is = (2/15) / (19/30) = 4/19
= 19/30
Probability of selecting a red ball from box P = (1/3) * (2/5) = 2/15
Given that a ball selected in the above process is a red ball, the probability that it came from the box P is = (2/15) / (19/30) = 4/19
When a coin is tossed, the probability of getting a Head is  . Let be the random variable denoting the number of tosses till the first Head appears, including the toss where the Head appears. Assuming that successive tosses are independent, the expected value of N is
. Let be the random variable denoting the number of tosses till the first Head appears, including the toss where the Head appears. Assuming that successive tosses are independent, the expected value of N is- a)1/p
- b)1/(1 - p)
- c)1/p2
- d)1/(1 - p2)
Correct answer is option 'A'. Can you explain this answer?
When a coin is tossed, the probability of getting a Head is  . Let be the random variable denoting the number of tosses till the first Head appears, including the toss where the Head appears. Assuming that successive tosses are independent, the expected value of N is
. Let be the random variable denoting the number of tosses till the first Head appears, including the toss where the Head appears. Assuming that successive tosses are independent, the expected value of N is
a)
1/p
b)
1/(1 - p)
c)
1/p2
d)
1/(1 - p2)
|
|
Yash Patel answered |
multiply both side with and subtract:
If P and Q are two random events, then the following is TRUE:- a)Independence of P and Q implies that probability (P ∩ Q) = 0
- b)Probability (P ∪ Q) ≥ Probability (P) + Probability (Q)
- c)If P and Q are mutually exclusive, then they must be independent
- d)Probability (P ∩ Q) ≤ Probability (P)
Correct answer is option 'D'. Can you explain this answer?
If P and Q are two random events, then the following is TRUE:
a)
Independence of P and Q implies that probability (P ∩ Q) = 0
b)
Probability (P ∪ Q) ≥ Probability (P) + Probability (Q)
c)
If P and Q are mutually exclusive, then they must be independent
d)
Probability (P ∩ Q) ≤ Probability (P)
|
|
Yash Patel answered |
here i check option---> i let P = probability, P and Q is replaced by A and B.
A) it is saying independent means P(A ^ B) = P(A)* P(B) so option A is false
B) P(AÜ B) = P(A) + P(B) - P(A ^ B)
hence P(AÜB) >= P(A) + P(B) its false option B is false
C) if A and B is mutually exclusive means P(A ^ B) = 0 then its independent ........its false there is no relation independent and mutually exclusive
D) P(A ^ B) <= P(A)
A) it is saying independent means P(A ^ B) = P(A)* P(B) so option A is false
B) P(AÜ B) = P(A) + P(B) - P(A ^ B)
hence P(AÜB) >= P(A) + P(B) its false option B is false
C) if A and B is mutually exclusive means P(A ^ B) = 0 then its independent ........its false there is no relation independent and mutually exclusive
D) P(A ^ B) <= P(A)
its true
hence option D is correct
How many different non-isomorphic Abelian groups of order 4 are there- a)2
- b)3
- c)4
- d)5
Correct answer is option 'A'. Can you explain this answer?
How many different non-isomorphic Abelian groups of order 4 are there
a)
2
b)
3
c)
4
d)
5

|
Pankaj Rane answered |
2 can be written as 2 power 2.
Number of partitioning of 2 = no. of non isomorphic abelian groups
2 can be partitioned as {(2),(1,1)}
Number of partitioning of 2 = no. of non isomorphic abelian groups
2 can be partitioned as {(2),(1,1)}
What is the number of vertices in an undirected connected graph with 27 edges, 6 vertices of degree 2, 3 vertices of degree 4 and remaining of degree 3?- a)10
- b)11
- c)18
- d)19
Correct answer is option 'D'. Can you explain this answer?
What is the number of vertices in an undirected connected graph with 27 edges, 6 vertices of degree 2, 3 vertices of degree 4 and remaining of degree 3?
a)
10
b)
11
c)
18
d)
19

|
Telecom Tuners answered |
The idea is to use Handshaking Lemma :- In any graph, the sum of all the vertex-degree is equal to twice the number of edges.
Let x = Number of vertices of degree 3.
By Handshaking Lemma
6*2 + 3*4 + (x-9)*3 = 27*2
24 + (x-9)*3 = 54
x-9 = 10
x = 19
By Handshaking Lemma
6*2 + 3*4 + (x-9)*3 = 27*2
24 + (x-9)*3 = 54
x-9 = 10
x = 19
A graph is self-complementary if it is isomorphic to its complement. For all self-complementary graphs on n vertices, n is- a)A multiple of 4
- b)Even
- c)Odd
- d)Congruent to 0 mod 4, or 1 mod 4
Correct answer is option 'D'. Can you explain this answer?
A graph is self-complementary if it is isomorphic to its complement. For all self-complementary graphs on n vertices, n is
a)
A multiple of 4
b)
Even
c)
Odd
d)
Congruent to 0 mod 4, or 1 mod 4
|
|
Ujwal Nambiar answered |
Explanation:
In order to understand why the correct answer is option 'D', let's break down the given options and analyze them one by one.
Option A: A multiple of 4
A graph being self-complementary doesn't have any direct relation to the number of vertices being a multiple of 4. There are self-complementary graphs with any number of vertices, not just multiples of 4. Therefore, option A is incorrect.
Option B: Even
This option is also incorrect because self-complementary graphs can have an odd number of vertices. There are self-complementary graphs with 3, 5, 7, etc. vertices.
Option C: Odd
Similar to the previous option, self-complementary graphs can have an odd number of vertices. Therefore, option C is incorrect.
Option D: Congruent to 0 mod 4, or 1 mod 4
This option is correct. A graph being self-complementary is related to its number of vertices modulo 4.
Let's consider the two cases:
- If the number of vertices is congruent to 0 modulo 4 (i.e., a multiple of 4), then we can divide the vertices into two equal sets of size n/2. In the complement of the graph, each vertex in one set is adjacent to every vertex in the other set. When we swap the adjacency relationships, we get an isomorphic graph, making it self-complementary.
- If the number of vertices is congruent to 1 modulo 4, then we can divide the vertices into two sets, one with (n+1)/2 vertices and the other with (n-1)/2 vertices. In the complement of the graph, each vertex in the larger set is adjacent to every vertex in the smaller set. Again, swapping the adjacency relationships results in an isomorphic graph, making it self-complementary.
Therefore, self-complementary graphs on n vertices are congruent to 0 mod 4 or 1 mod 4.
A box contains 20 defective items and 80 non-defective items. If two items are selected at random without replacement, what will be the probability that both items are defective? - a)1/5
- b)1/25
- c)20/99
- d)11/495
Correct answer is option 'D'. Can you explain this answer?
A box contains 20 defective items and 80 non-defective items. If two items are selected at random without replacement, what will be the probability that both items are defective?
a)
1/5
b)
1/25
c)
20/99
d)
11/495

|
Kaavya Sengupta answered |
Total number of items = 100
Number of defective items = 20
Number of Non-defective items = 80
Then the probability that both items are defective, when 2 items are selected at random is,
⇒ P= (20C2x80C0)/(100C2) = 19/495
"If X, then Y unless Z" is represented by which of the following formulae in propositional logic? ("¬" is negation "^" is conjunction, and "→" is implication)- a)(X ^ ¬ Z) → Y
- b)(X ^ Y) → ¬ Z
- c)(X → (Y ^ ¬ Z)
- d)(X → Y(^ ¬ Z)
Correct answer is option 'A'. Can you explain this answer?
"If X, then Y unless Z" is represented by which of the following formulae in propositional logic? ("¬" is negation "^" is conjunction, and "→" is implication)
a)
(X ^ ¬ Z) → Y
b)
(X ^ Y) → ¬ Z
c)
(X → (Y ^ ¬ Z)
d)
(X → Y(^ ¬ Z)
|
|
Ravi Singh answered |
The statement "If X then Y unless Z" means, if Z doesn't occur, X implies Y i.e. ¬Z→(X→Y), which is equivalent to Z∨(X→Y) (since P→Q ≡ ¬P∨Q), which is then equivalent to Z∨(¬X∨Y). Now we can look into options which one matches with this.
So option (a) is (X∧¬Z)→Y = ¬((X∧¬Z))∨Y = (¬X∨Z)∨Y, which matches our expression. So option A is correct.
So option (a) is (X∧¬Z)→Y = ¬((X∧¬Z))∨Y = (¬X∨Z)∨Y, which matches our expression. So option A is correct.
Let A be an mxn matrix and B an nxm matrix.
It is given that determinant (Im + AB) = determinant (In + BA) , where Ik is the k×k identity matrix. Using the above property, the determinant of the matrix given below is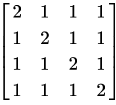
- a)2
- b)5
- c)8
- d)16
Correct answer is option 'B'. Can you explain this answer?
Let A be an mxn matrix and B an nxm matrix.
It is given that determinant (Im + AB) = determinant (In + BA) , where Ik is the k×k identity matrix. Using the above property, the determinant of the matrix given below is
It is given that determinant (Im + AB) = determinant (In + BA) , where Ik is the k×k identity matrix. Using the above property, the determinant of the matrix given below is
a)
2
b)
5
c)
8
d)
16
|
|
Shanaya Chavan answered |
You have to play three games with opponents A and B in a specified sequence. You win the series if you win two consecutive games. A is a stronger player than B. Which sequence maximizes your chance of winning the series?- a)AAB
- b)ABA
- c)BAB
- d)BAA
- e)All are the same.
Correct answer is option 'B'. Can you explain this answer?
You have to play three games with opponents A and B in a specified sequence. You win the series if you win two consecutive games. A is a stronger player than B. Which sequence maximizes your chance of winning the series?
a)
AAB
b)
ABA
c)
BAB
d)
BAA
e)
All are the same.
|
|
Yash Patel answered |
Let the probability of winning against player A be and the probability of winning against player B be b.
We can see that not all probabilities are equal, so option E is not correct.
We can also see that options A and D result in the same value, so they are not correct either.
Comparing option B and option C.
Hence, option B is the correct answer.
Chapter doubts & questions for Discrete Mathematics - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Discrete Mathematics - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
453 videos|1305 docs|700 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup










