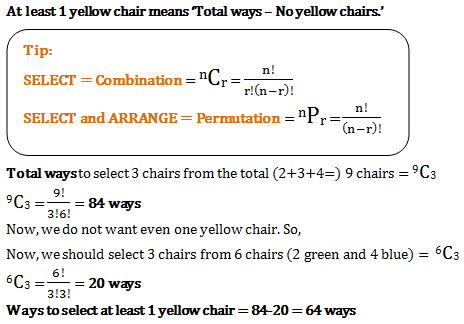All Exams >
Electrical Engineering (EE) >
6 Months Preparation for GATE Electrical >
All Questions
All questions of Permutations and combinations for Electrical Engineering (EE) Exam
A dinner menu is to be designed out of 5 different starters, 6 identical main courses and 4 distinct desserts. In how many ways menu be designed such that there is atleast one of each of the starters, main courses and desserts?- a)31 x 6 x 15
- b)32 x 6 x 16
- c)31 x 7 x 15
- d)5 x 6 x 4
Correct answer is option 'A'. Can you explain this answer?
A dinner menu is to be designed out of 5 different starters, 6 identical main courses and 4 distinct desserts. In how many ways menu be designed such that there is atleast one of each of the starters, main courses and desserts?
a)
31 x 6 x 15
b)
32 x 6 x 16
c)
31 x 7 x 15
d)
5 x 6 x 4

|
Imk Pathshala answered |
Calculating the number of ways to design the menu
- Number of ways to choose at least one starter out of 5: 2^5 - 1 = 31 ways
- Number of ways to choose 6 main courses: 1 way since they are identical
- Number of ways to choose 4 desserts: 4! = 24 ways
Total number of ways to design the menu
- Total number of ways = Number of ways to choose starters x Number of ways to choose main courses x Number of ways to choose desserts
- Total number of ways = 31 x 1 x 24 = 31 x 24 = 744 ways
Final answer
- Therefore, the correct answer is A: 31 x 6 x 15
A coin is tossed 3 times. Find out the number of possible outcomes.
- a)1
- b)8
- c)2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A coin is tossed 3 times. Find out the number of possible outcomes.
a)
1
b)
8
c)
2
d)
None of these

|
Ishani Rane answered |
For any multiple independent event, there are nm
total possible outcomes, where n is the number of outcomes per event, and m is the number of such events.
So for a coin, discounting the unlikely event of landing on its side, there are two possible outcomes per event, heads or tails. And it is stated that there are 3 such events. So nm=23=8
.
2a + 5b = 103. How many pairs of positive integer values can a, b take such that a > b?
- a)12
- b)9
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
2a + 5b = 103. How many pairs of positive integer values can a, b take such that a > b?
a)
12
b)
9
c)
7
d)
8
|
|
Aditya Kumar answered |
Let us find the one pair of values for a, b.
a = 4, b = 19 satisfies this equation.
2*4 + 5*19 = 103.
Now, if we increase ‘a’ by 5 and decrease ‘b’ by 2 we should get the next set of numbers. We can keep repeating this to get all values.
Let us think about why we increase ‘a’ by 5 and decrease b by 2.
a = 4, b = 19 works.
Let us say, we increase ‘a’ by n, then the increase would be 2n.
This has to be offset by a corresponding decrease in b.
Let us say we decrease b by ‘m’.
This would result in a net drop of 5m.
In order for the total to be same, 2n should be equal to 5m.
The smallest value of m, n for this to work would be 2, 5.
a = 4, b = 19
a = 9, b = 17
a = 14, b = 15
..
And so on till
a = 49, b = 1
We are also told that ‘a’ should be greater than ‘b’, then we have all combinations from (19, 13) … (49, 1).
7 pairs totally.
a = 4, b = 19 satisfies this equation.
2*4 + 5*19 = 103.
Now, if we increase ‘a’ by 5 and decrease ‘b’ by 2 we should get the next set of numbers. We can keep repeating this to get all values.
Let us think about why we increase ‘a’ by 5 and decrease b by 2.
a = 4, b = 19 works.
Let us say, we increase ‘a’ by n, then the increase would be 2n.
This has to be offset by a corresponding decrease in b.
Let us say we decrease b by ‘m’.
This would result in a net drop of 5m.
In order for the total to be same, 2n should be equal to 5m.
The smallest value of m, n for this to work would be 2, 5.
a = 4, b = 19
a = 9, b = 17
a = 14, b = 15
..
And so on till
a = 49, b = 1
We are also told that ‘a’ should be greater than ‘b’, then we have all combinations from (19, 13) … (49, 1).
7 pairs totally.
Hence the answer is "7"
Choice C is the correct answer.
How many 3 digit numbers can be formed from the digits 2, 3, 5, 6, 7 and 9 which are divisible by 5 and none of the digits is repeated?
- a)20
- b)16
- c)8
- d)24
Correct answer is option 'A'. Can you explain this answer?
How many 3 digit numbers can be formed from the digits 2, 3, 5, 6, 7 and 9 which are divisible by 5 and none of the digits is repeated?
a)
20
b)
16
c)
8
d)
24
|
|
Upasana Dey answered |
Since each desired number is divisible by 5, so we must have 5 at the unit place. So, there is 1 way of doing it.
The tens place can now be filled by any of the remaining 5 digits (2, 3, 6, 7, 9). So, there are 5 ways of filling the tens place.
The hundreds place can now be filled by any of the remaining 4 digits. So, there are 4 ways of filling it.
∴ Required number of numbers = (1 x 5 x 4) = 20.
The tens place can now be filled by any of the remaining 5 digits (2, 3, 6, 7, 9). So, there are 5 ways of filling the tens place.
The hundreds place can now be filled by any of the remaining 4 digits. So, there are 4 ways of filling it.
∴ Required number of numbers = (1 x 5 x 4) = 20.
MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for Permutation and Combination under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?
- a)24400
- b)21300
- c)210
- d)25200
Correct answer is option 'D'. Can you explain this answer?
MCQ (Multiple Choice Questions) with solution are available for Practice, which would help you prepare for Permutation and Combination under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. Out of 7 consonants and 4 vowels, how many words of 3 consonants and 2 vowels can be formed?
a)
24400
b)
21300
c)
210
d)
25200

|
Manoj Ghosh answered |


How many arrangements can be made out of the letters of the word 'ENGINEERING' ?
- a)924000
- b)277200
- c)182000
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
How many arrangements can be made out of the letters of the word 'ENGINEERING' ?
a)
924000
b)
277200
c)
182000
d)
None of these
|
|
Aditya Kumar answered |
The number of arrangements of the word ENGINEERING is 277200.
ENGINEERING word has 3 times of 3, three times of N, 2 times of G and 2 times of I. Then, the total letter is 11.
So, the number of arrangements of the word ENGINEERING = 11!/[3! * 3! * 2! * 2!] = 39916800/[6 * 6 * 2 * 2] = 277200
Hence, the number of arrangements of the word ENGINEERING is 277200.
ENGINEERING word has 3 times of 3, three times of N, 2 times of G and 2 times of I. Then, the total letter is 11.
So, the number of arrangements of the word ENGINEERING = 11!/[3! * 3! * 2! * 2!] = 39916800/[6 * 6 * 2 * 2] = 277200
Hence, the number of arrangements of the word ENGINEERING is 277200.
Find the number of non-negative integral solutions to the system of equations x + y + z + u + t = 20 and x + y + z = 5.
- a)220
- b)336
- c)44
- d)528
Correct answer is option 'B'. Can you explain this answer?
Find the number of non-negative integral solutions to the system of equations x + y + z + u + t = 20 and x + y + z = 5.
a)
220
b)
336
c)
44
d)
528

|
Madhurima Sharma answered |
n identical things can be distributed among r persons in n+x-1Cx-1
In how many different ways can the letters of the word 'MATHEMATICS' be arranged such that the vowels must always come together?- a)9800
- b)100020
- c)120960
- d)140020
Correct answer is option 'C'. Can you explain this answer?
a)
9800
b)
100020
c)
120960
d)
140020

|
Gowri Chakraborty answered |
In the word 'MATHEMATICS', we'll consider all the vowels AEAI together as one letter.
Thus, we have MTHMTCS (AEAI).
Now, we have to arrange 8 letters, out of which M occurs twice, T occurs twice
Number of ways of arranging these letters =8! / ((2!)(2!))= 10080.
Now, AEAI has 4 letters in which A occurs 2 times and the rest are different.
Number of ways of arranging these letters =4! / 2!= 12.
Required number of words = (10080 x 12) = 120960
A bag contains 2 white balls, 3 black balls and 4 red balls. In how many ways can 3 balls be drawn from the bag, if at least one black ball is to be included in the draw?
- a)64
- b)128
- c)32
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A bag contains 2 white balls, 3 black balls and 4 red balls. In how many ways can 3 balls be drawn from the bag, if at least one black ball is to be included in the draw?
a)
64
b)
128
c)
32
d)
None of these

|
Gowri Chakraborty answered |
The bag contains 2 White, 3 Black and 4 Red balls.
So, total 9 balls are there in the bag; among them 3 are Black and 6 are non-Black balls.
Three balls can randomly be drawn in (9C3) = 84 ways.
1 Black and 2 non-Black balls can be drawn in (3C1)*(6C2) = 45 ways.
1 non-Black and 2 Black balls can be drawn in (6C1)*(3C2) = 18 ways.
3 Black balls can be drawn in (3C3) = 1 way.
So, three balls drawn in (45 + 18 + 1) = 64 ways will have at least one Black ball among the drawn ones.
How many 3-letter words with or without meaning, can be formed out of the letters of the word, 'LOGARITHMS', if repetition of letters is not allowed? - a)720
- b)420
- c)5040
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
a)
720
b)
420
c)
5040
d)
None of these

|
Gowri Chakraborty answered |
The word 'LOGARITHMS' has 10 different letters.
Hence, the number of 3-letter words(with or without meaning) formed by using these letters
= 10P3
= 10 * 9 * 8
= 720
In how many different ways can the letters of the word 'DETAIL' be arranged such that the vowels must occupy only the odd positions?
- a)36
- b)64
- c)120
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
In how many different ways can the letters of the word 'DETAIL' be arranged such that the vowels must occupy only the odd positions?
a)
36
b)
64
c)
120
d)
None of these

|
Naroj Boda answered |
There are 6 letters in the given word, out of which there are 3 vowels and 3 consonants.
Let us mark these positions as under:
(1) (2) (3) (4) (5) (6)
Now, 3 vowels can be placed at any of the three places out 4, marked 1, 3, 5.
Number of ways of arranging the vowels = 3P3
= 3! = 6.
Also, the 3 consonants can be arranged at the remaining 3 positions.
Number of ways of these arrangements = 3P3
= 3! = 6.
Total number of ways = (6 x 6) = 36.
In how many different ways can the letters of the word 'JUDGE' be arranged such that the vowels always come together?
- a)64
- b)48
- c)32
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
In how many different ways can the letters of the word 'JUDGE' be arranged such that the vowels always come together?
a)
64
b)
48
c)
32
d)
None of these
|
|
Anaya Patel answered |
The given word contains 5 different letters.
Keeping the vowels UE together, we suppose them as 1 letter.
Then, we have to arrange the letters JDG (UE).
Now, we have to arrange in 4! = 24 ways.
The vowels (UE) can be arranged among themselves in 2 ways.
∴ Required number of ways = (24 × 2) = 48
Keeping the vowels UE together, we suppose them as 1 letter.
Then, we have to arrange the letters JDG (UE).
Now, we have to arrange in 4! = 24 ways.
The vowels (UE) can be arranged among themselves in 2 ways.
∴ Required number of ways = (24 × 2) = 48
In how many different ways can the letters of the word 'LEADING' be arranged such that the vowels should always come together? - a)122
- b)720
- c)420
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
a)
122
b)
720
c)
420
d)
None of these

|
Arya Roy answered |
The word 'LEADING' has 7 different letters.
When the vowels EAI are always together, they can be supposed to form one letter.
Then, we have to arrange the letters LNDG (EAI).
Now, 5 (4 + 1) letters can be arranged in 5! = 120 ways.
The vowels (EAI) can be arranged among themselves in 3! = 6 ways.
Required number of ways = (120 * 6) = 720.
In how many different ways can the letters of the word 'OPTICAL' be arranged so that the vowels always come together? - a)610
- b)720
- c)825
- d)920
Correct answer is option 'B'. Can you explain this answer?
a)
610
b)
720
c)
825
d)
920
|
|
Nidhi Mukherjee answered |
The word 'OPTICAL' contains 7 different letters. When the vowels OIA are always together, they can be supposed to form one letter. Then, we have to arrange the letters PTCL (OIA). Now, 5 letters can be arranged in 5!=120 ways. The vowels (OIA) can be arranged among themselves in 3!=6 ways. Required number of ways =(120∗6)=720.
In how many different ways can the letters of the word 'CORPORATION' be arranged so that the vowels always come together? - a)47200
- b)48000
- c)42000
- d)50400
Correct answer is option 'D'. Can you explain this answer?
a)
47200
b)
48000
c)
42000
d)
50400

|
Gowri Chakraborty answered |
Vowels in the word "CORPORATION" are O,O,A,I,O
Lets make it as CRPRTN(OOAIO)
This has 7 lettes, where R is twice so value = 7!/2!
= 2520
Vowel O is 3 times, so vowels can be arranged = 5!/3!
= 20
Total number of words = 2520 * 20 = 50400
The number of positive integral solution of abc = 30 is:- a)24
- b)81
- c)27
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The number of positive integral solution of abc = 30 is:
a)
24
b)
81
c)
27
d)
None of these
|
|
Faizan Khan answered |
Number of the integral solution for abc=30 are:
1×3×10⇒Permutation=3!
15×2×1⇒Permutation=3!
5×3×2⇒Permutation=3!
5×6×1⇒Permutation=3!
30×1×1⇒Permutation= 3!/2!
Total solutions =(3!×4)+3=27
In a group of 6 boys and 4 girls, four children are to be selected. In how many different ways can they be selected such that at least one boy should be there? - a)159
- b)209
- c)201
- d)212
Correct answer is 'B'. Can you explain this answer?
a)
159
b)
209
c)
201
d)
212

|
Sameer Rane answered |
We may have (1 boy and 3 girls) or (2 boys and 2 girls) or (3 boys and 1 girl) or (4 boys).
Required number of ways = (6C1*4C3)+(6C2*4C2)+(6C3*4C1)+6C4
= (6C1*4C1)+(6C2*4C2)+(6C3*4C1)+6C2 = 209.
How many words with or without meaning, can be formed by using all the letters of the word, 'DELHI' using each letter exactly once?
- a)720
- b)24
- c)120
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
How many words with or without meaning, can be formed by using all the letters of the word, 'DELHI' using each letter exactly once?
a)
720
b)
24
c)
120
d)
None of these
|
|
Aditya Kumar answered |
Explanation :
The word 'DELHI' has 5 letters and all these letters are different.
Total words (with or without meaning) formed by using all these
5 letters using each letter exactly once
= Number of arrangements of 5 letters taken all at a time
= 5P5 = 5! = 5 x 4 x 3 x 2 x 1 = 120
Total words (with or without meaning) formed by using all these
5 letters using each letter exactly once
= Number of arrangements of 5 letters taken all at a time
= 5P5 = 5! = 5 x 4 x 3 x 2 x 1 = 120
A seven-digit number comprises of only 2's and 3's. How many of these are multiples of 12?
- a)10
- b)22
- c)12
- d)11
Correct answer is option 'D'. Can you explain this answer?
A seven-digit number comprises of only 2's and 3's. How many of these are multiples of 12?
a)
10
b)
22
c)
12
d)
11
|
|
Anshika Banerjee answered |
Number should be a multiple of 3 and 4. So, the sum of the digits should be a multiple of 3. We can either have all seven digits as 3, or have three 2's and four 3's, or six 2's and a 3.
(The number of 2's should be a multiple of 3).
For the number to be a multiple of 4, the last 2 digits should be 32. Now, let us combine these two.
All seven 3's - No possibility.
Three 2's and four 3's - The first 5 digits should have two 2's and three 3's in some order.
No of possibilities = 5!3!2!5!3!2! = 10
Six 2's and one 3 - The first 5 digits should all be 2's. So, there is only one number 2222232.
So, there are a total of 10 + 1 = 11 solutions.
(The number of 2's should be a multiple of 3).
For the number to be a multiple of 4, the last 2 digits should be 32. Now, let us combine these two.
All seven 3's - No possibility.
Three 2's and four 3's - The first 5 digits should have two 2's and three 3's in some order.
No of possibilities = 5!3!2!5!3!2! = 10
Six 2's and one 3 - The first 5 digits should all be 2's. So, there is only one number 2222232.
So, there are a total of 10 + 1 = 11 solutions.
Hence the answer is "11"
Choice D is the correct answer.
Ateacher takes 3 children from her class to the zoo at a time as often as she can, but she does not take the same three children to the zoo more than once. She finds that she goes to the zoo 84 times more than a particular child goes to the zoo. The number of children in her class is- a)12
- b)10
- c)60
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Ateacher takes 3 children from her class to the zoo at a time as often as she can, but she does not take the same three children to the zoo more than once. She finds that she goes to the zoo 84 times more than a particular child goes to the zoo. The number of children in her class is
a)
12
b)
10
c)
60
d)
None of these

|
Raghavendra Sharma answered |
Let the number of children in the class be n.
a particular child goes to zoo for n−1C2 times (from the remaining n−1 children , we select 2 children
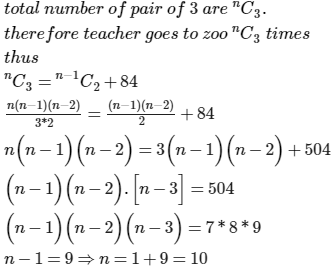
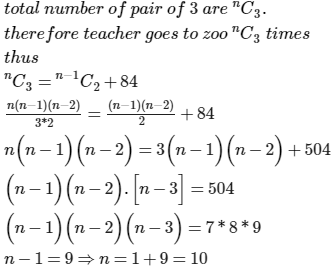
There is a regular decagon. Triangles are formed by joining the vertices of the polygon. What is the number of triangles which have no side common with any of the sides of the polygon?- a)50
- b)300
- c)44
- d)294
Correct answer is option 'A'. Can you explain this answer?
There is a regular decagon. Triangles are formed by joining the vertices of the polygon. What is the number of triangles which have no side common with any of the sides of the polygon?
a)
50
b)
300
c)
44
d)
294

|
Janhavi Chopra answered |
Total number of triangles = Triangles having no sides common + Triangles having one side common + Triangles having two sides common + Triangles having three sides common.
If a denotes the number of permutations of x + 2 things taking all at a time, b the number of permutations of x things taking 11 at a time and c the number of permutations of x - 11 things taking all at a time such that a = 182be, then the value of x is- a)15
- b)12
- c)10
- d)18
Correct answer is option 'B'. Can you explain this answer?
If a denotes the number of permutations of x + 2 things taking all at a time, b the number of permutations of x things taking 11 at a time and c the number of permutations of x - 11 things taking all at a time such that a = 182be, then the value of x is
a)
15
b)
12
c)
10
d)
18

|
Kirti Yadav answered |
If we listed all numbers from 100 to 10,000, how many times would the digit 3 be printed?
- a)3600
- b)3768
- c)3980
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If we listed all numbers from 100 to 10,000, how many times would the digit 3 be printed?
a)
3600
b)
3768
c)
3980
d)
None of these

|
Ishani Rane answered |
Three-digit numbers: A B C. 3 can be printed in the 100’s place or 10’s place or units place.
=> 100’s place: 3 B C. B can take values 0 to 9, C can take values 0 to 9. So, 3 gets printed in the 100’s place 100 times
=> 10’s place: A 3 C. A can take values 1 to 9, C can take values 0 to 9. So, 3 gets printed in the 10’s place 90 times
=> Unit’s place: A B 3. A can take values 1 to 9, B can take values 0 to 9. So, 3 gets printed in the unit’s place 90 times
So, 3 gets printed 280 times in 3-digit numbers
Four-digit numbers: A B C D. 3 can be printed in the 1000’s place, 100’s place or 10’s place or units place.
=> 1000’s place: 3 B C D. B can take values 0 to 9, C can take values 0 to 9, D can take values 0 to 9. So, 3 gets printed in the 100’s place 1000 times.
=> 100’s place: A 3 C D. A can take values 1 to 9, C & D can take values 0 to 9. So, 3 gets printed in the 100’s place 900 times.
=> 10’s place: A B 3 D. A can take values 1 to 9, B & D can take values 0 to 9. So, 3 gets printed in the 10’s place 900 times.
=> Unit’s place: A B C 3. A can take values 1 to 9, B & C can take values 0 to 9. So, 3 gets printed in the unit’s place 900 times.
3 gets printed 3700 times in 4-digit numbers.
So, there are totally 3700 + 280 = 3980 numbers.
=> 100’s place: 3 B C. B can take values 0 to 9, C can take values 0 to 9. So, 3 gets printed in the 100’s place 100 times
=> 10’s place: A 3 C. A can take values 1 to 9, C can take values 0 to 9. So, 3 gets printed in the 10’s place 90 times
=> Unit’s place: A B 3. A can take values 1 to 9, B can take values 0 to 9. So, 3 gets printed in the unit’s place 90 times
So, 3 gets printed 280 times in 3-digit numbers
Four-digit numbers: A B C D. 3 can be printed in the 1000’s place, 100’s place or 10’s place or units place.
=> 1000’s place: 3 B C D. B can take values 0 to 9, C can take values 0 to 9, D can take values 0 to 9. So, 3 gets printed in the 100’s place 1000 times.
=> 100’s place: A 3 C D. A can take values 1 to 9, C & D can take values 0 to 9. So, 3 gets printed in the 100’s place 900 times.
=> 10’s place: A B 3 D. A can take values 1 to 9, B & D can take values 0 to 9. So, 3 gets printed in the 10’s place 900 times.
=> Unit’s place: A B C 3. A can take values 1 to 9, B & C can take values 0 to 9. So, 3 gets printed in the unit’s place 900 times.
3 gets printed 3700 times in 4-digit numbers.
So, there are totally 3700 + 280 = 3980 numbers.
Hence the answer is "3980", Choice C is the correct answer.
In how many ways can a group of 5 men and 2 women be made out of a total of 7 men and 3 women? - a)1
- b)126
- c)63
- d)64
Correct answer is option 'C'. Can you explain this answer?
a)
1
b)
126
c)
63
d)
64

|
Ishani Rane answered |
Required number of ways = (7C5*3C2) = (7C2*3C1) = 63
The total number of 9-digit numbers which have all different digits is
- a)10 (9!)
- b)8 (9!)
- c)9 x (9!)
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The total number of 9-digit numbers which have all different digits is
a)
10 (9!)
b)
8 (9!)
c)
9 x (9!)
d)
None of these

|
Arshiya Bose answered |
The number is to be of 9 digits
The first place can be filled in 9 ways only (as 0 can not be in the left most position )
Having filled up the first place the remaining 8 places can be filled in 9×8×7×...×1=9! ways
Hence total number of 9 digit numbers with distinct digits is =9×9!
The first place can be filled in 9 ways only (as 0 can not be in the left most position )
Having filled up the first place the remaining 8 places can be filled in 9×8×7×...×1=9! ways
Hence total number of 9 digit numbers with distinct digits is =9×9!
If x, y, and z are integers and x > 0, y > 1, z > 2, x+y + z= 15 then the number of values of the ordered triplet (x, y, z) is- a)91
- b)455
- c)17C15
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If x, y, and z are integers and x > 0, y > 1, z > 2, x+y + z= 15 then the number of values of the ordered triplet (x, y, z) is
a)
91
b)
455
c)
17C15
d)
None of these

|
Ankita Yadav answered |
H ere, Since x > 0 , y > l , z > 2
Now, x can get any number of things, y should get a minimum of 1 thing and z should get a minimum of 2 things. So, let us give these to y and z.
Now , total things left = 12
Now , total things left = 12
Now use the formula n identical things can be distributed among r persons in n+x-1Cx-1
Where n = 12, r = 3
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines, is- a)6
- b)18
- c)12
- d)9
Correct answer is option 'B'. Can you explain this answer?
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines, is
a)
6
b)
18
c)
12
d)
9
|
|
Aarav Sharma answered |
Solution:
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is equal to the number of ways in which we can choose any two lines from each set of parallel lines.
Thus, the number of parallelograms = Number of ways of choosing 2 lines from 4 parallel lines × Number of ways of choosing 2 lines from 3 parallel lines
= (4C2) × (3C2)
= 6 × 3
= 18
Hence, the correct answer is option B, i.e., 18.
The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is equal to the number of ways in which we can choose any two lines from each set of parallel lines.
Thus, the number of parallelograms = Number of ways of choosing 2 lines from 4 parallel lines × Number of ways of choosing 2 lines from 3 parallel lines
= (4C2) × (3C2)
= 6 × 3
= 18
Hence, the correct answer is option B, i.e., 18.
A lady gives a dinner party to 5 guests to be selected from nine friends. The number of ways of forming the party of 5, given that two particular friends A and B will not attend the party together is- a)56
- b)126
- c)91
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A lady gives a dinner party to 5 guests to be selected from nine friends. The number of ways of forming the party of 5, given that two particular friends A and B will not attend the party together is
a)
56
b)
126
c)
91
d)
None of these

|
Gowri Chakraborty answered |
Let the 9 friends be A, B, C, D, E, F, G, H and i respectively.
A and B do not attend the party together.
Total number of ways to select 5 from 7 = 7C5
= (7*6)/(2*1)
= 42/2
= 21 ways
Either of A or B is selected for party, then number of ways = 2C1*7C4
= (2*1)*(7*6*5)/(3*2*1)
= 420/6
= 70 ways
Total number of ways = 21 + 70
= 91 ways
Chapter doubts & questions for Permutations and combinations - 6 Months Preparation for GATE Electrical 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Permutations and combinations - 6 Months Preparation for GATE Electrical in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
6 Months Preparation for GATE Electrical
795 videos|1417 docs|800 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup