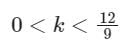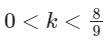All Exams >
Electrical Engineering (EE) >
6 Months Preparation for GATE Electrical >
All Questions
All questions of Routh-Hurwitz Stability for Electrical Engineering (EE) Exam
A Routh table is shown in fig. The location of pole on RHP, LHP and imaginary axis are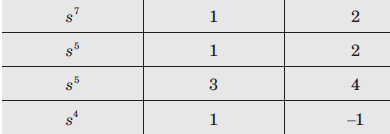
- a)1, 2, 4
- b)1, 6, 0
- c)1, 0, 6
- d)None of the above
Correct answer is 'A'. Can you explain this answer?
A Routh table is shown in fig. The location of pole on RHP, LHP and imaginary axis are
a)
1, 2, 4
b)
1, 6, 0
c)
1, 0, 6
d)
None of the above

|
Jaya Yadav answered |
If the system is given with the unbounded input then nothing can be clarified for the stability of the system.
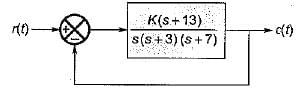
For which of the following values of K, the feedback system shown in the below figure is stable?
- a)K < 0
- b)K > 0
- c)0 < K < 54
- d)0 < K < 70
Correct answer is option 'D'. Can you explain this answer?
For which of the following values of K, the feedback system shown in the below figure is stable?


a)
K < 0
b)
K > 0
c)
0 < K < 54
d)
0 < K < 70
|
|
Rhea Reddy answered |
The characteristic equation is
1 + G (s) H (s) = 0
or,
1 + G (s) H (s) = 0
or,
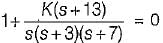
or, s3 + 10s2 + (21 + K )s + 13 K= 0

For stability, 13K > 0 or K > 0
Also,
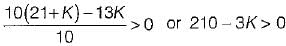
or, K < 70
Hence, 0 < K< 70 (For stability).
Consider the following statements regarding the characteristic equation of a system given by:
s4 + 5s3 + 25+10 = 0
1. The system is unstable.
2. The system is stable.
3. Number of roots with zero real part - 0
4. Number of roots with positive real part - 4
5. Number of roots with negative real part = 2
Which of the above statements are correct?- a)2 and 3
- b)1 and 3
- c)2, 3 and 4
- d)1, 3 and 5
Correct answer is option 'D'. Can you explain this answer?
Consider the following statements regarding the characteristic equation of a system given by:
s4 + 5s3 + 25+10 = 0
1. The system is unstable.
2. The system is stable.
3. Number of roots with zero real part - 0
4. Number of roots with positive real part - 4
5. Number of roots with negative real part = 2
Which of the above statements are correct?
s4 + 5s3 + 25+10 = 0
1. The system is unstable.
2. The system is stable.
3. Number of roots with zero real part - 0
4. Number of roots with positive real part - 4
5. Number of roots with negative real part = 2
Which of the above statements are correct?
a)
2 and 3
b)
1 and 3
c)
2, 3 and 4
d)
1, 3 and 5
|
|
Anirban Gupta answered |
The Routh’s array is
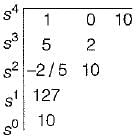
Since there are two sign changes in first column of Routh’s array, therefore the system is unstable.
Number of roots with positive real part = 2
Number of roots with negative real part = 2
Number of roots with zero real part = 0

Since there are two sign changes in first column of Routh’s array, therefore the system is unstable.
Number of roots with positive real part = 2
Number of roots with negative real part = 2
Number of roots with zero real part = 0
The transfer function of a system is 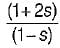
The system is then which one of the following?- a)Non-minimum phase function
- b)Low-pass system
- c)Second-order system
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
The transfer function of a system is 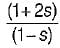
The system is then which one of the following?
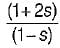
The system is then which one of the following?
a)
Non-minimum phase function
b)
Low-pass system
c)
Second-order system
d)
None of the above
|
|
Ashutosh Majumdar answered |
Since one pole (s .= 1) lies in RH s-plane, therefore the system is unstable.
Which of the following is the correct statement?
A minimum phase network is one whose transfer function has- a)zeros in the right hand s-plane and poles in the left hand s-plane.
- b)zeros and poles in the left hand s-plane.
- c)zeros in the left hand s-plane and poles in the right hand s-plane.
- d)arbitrary distribution of zeros and poles in the S-plane.
Correct answer is option 'B'. Can you explain this answer?
Which of the following is the correct statement?
A minimum phase network is one whose transfer function has
A minimum phase network is one whose transfer function has
a)
zeros in the right hand s-plane and poles in the left hand s-plane.
b)
zeros and poles in the left hand s-plane.
c)
zeros in the left hand s-plane and poles in the right hand s-plane.
d)
arbitrary distribution of zeros and poles in the S-plane.
|
|
Anjali Choudhury answered |
Explanation:
Minimum Phase Network:
A minimum phase network is a type of linear time-invariant (LTI) system in which all the zeroes and poles of the transfer function lie in the left-half of the s-plane. The transfer function of a minimum phase network is a causal and stable function that can be factored into a product of two terms: a minimum phase term and a delay term. The minimum phase term has all its zeroes and poles in the left-half of the s-plane, while the delay term has a pole at the origin.
Transfer Function:
The transfer function of a minimum phase network is given by:
H(s) = e^(-Ds) * G(s)
where D is a positive constant, G(s) is the minimum phase transfer function, and e^(-Ds) is the delay term. The transfer function H(s) can be expressed as a product of the minimum phase term G(s) and the delay term e^(-Ds). The minimum phase term G(s) is a causal and stable function that has all its zeroes and poles in the left-half of the s-plane. The delay term e^(-Ds) is a non-causal and unstable function that has a pole at the origin.
Properties of Minimum Phase Network:
The following are some of the properties of a minimum phase network:
- All the zeroes and poles of the transfer function lie in the left-half of the s-plane.
- The step response of a minimum phase network is faster than that of a non-minimum phase network with the same magnitude response.
- The phase response of a minimum phase network is always less than or equal to the phase response of a non-minimum phase network with the same magnitude response.
- The impulse response of a minimum phase network decays faster than that of a non-minimum phase network with the same magnitude response.
Answer:
Option 'B' is the correct statement. A minimum phase network is one whose transfer function has zeros and poles in the left-hand s-plane.
Minimum Phase Network:
A minimum phase network is a type of linear time-invariant (LTI) system in which all the zeroes and poles of the transfer function lie in the left-half of the s-plane. The transfer function of a minimum phase network is a causal and stable function that can be factored into a product of two terms: a minimum phase term and a delay term. The minimum phase term has all its zeroes and poles in the left-half of the s-plane, while the delay term has a pole at the origin.
Transfer Function:
The transfer function of a minimum phase network is given by:
H(s) = e^(-Ds) * G(s)
where D is a positive constant, G(s) is the minimum phase transfer function, and e^(-Ds) is the delay term. The transfer function H(s) can be expressed as a product of the minimum phase term G(s) and the delay term e^(-Ds). The minimum phase term G(s) is a causal and stable function that has all its zeroes and poles in the left-half of the s-plane. The delay term e^(-Ds) is a non-causal and unstable function that has a pole at the origin.
Properties of Minimum Phase Network:
The following are some of the properties of a minimum phase network:
- All the zeroes and poles of the transfer function lie in the left-half of the s-plane.
- The step response of a minimum phase network is faster than that of a non-minimum phase network with the same magnitude response.
- The phase response of a minimum phase network is always less than or equal to the phase response of a non-minimum phase network with the same magnitude response.
- The impulse response of a minimum phase network decays faster than that of a non-minimum phase network with the same magnitude response.
Answer:
Option 'B' is the correct statement. A minimum phase network is one whose transfer function has zeros and poles in the left-hand s-plane.
According to Hurwitz criterion, the characteristic equation
s4 + 8s3 + 18s2 + 16s + 5 = 0 is
- a)Stable
- b)Marginally stable
- c)Conditionally stable
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
According to Hurwitz criterion, the characteristic equation
s4 + 8s3 + 18s2 + 16s + 5 = 0 is
a)
Stable
b)
Marginally stable
c)
Conditionally stable
d)
None of these

|
Engineers Adda answered |
Concept:
The Routh Stability Criterion is used to test the stability of an LTI system. The conditions for stability are:
- All the coefficients of the characteristic Equation must be present and must have the same sign.
- It is necessary and sufficient that each term of the first column of the Routh Array of the Characteristic Equation is positive for the system to be stable, i.e. there should not be any sign changes in the first column of each row.
- The number of sign changes represents the number of roots on the right side of the s-plane.
- If the first term in any row of Routh Array is zero while the rest of the row has at least one non-zero term. Because of this term, the terms in the next row will become infinite.
- When all elements in any row of the Routh array are zero. This condition indicates that there are symmetrical/imaginary roots in the s-plane.
Application:
A(s) = s4 + 8s3 + 18s2 + 16s + 5
Forming the Routh array, we get:
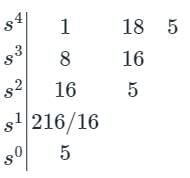
Since there are no sign changes in the first column of the Routh array, we conclude that the system is stable.
Consider the following statements related to Routh-Hurwitz criterion of determining the stability of a system:
1. It is applicable if the characteristic equation has real coefficients, complex ternrivS or exponential functions of s.
2. The criterion can be applied to any stability boundaries in complex plane, such as the unit circle in the z-plane.
3. The number of changes of signs in the elements of the first column equals the number of roots with negative real parts.
Which of these statements is/are not correct?- a)2 and 3 oniy .
- b)1, 2 and 3
- c)1 only
- d)1 and 2 only
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements related to Routh-Hurwitz criterion of determining the stability of a system:
1. It is applicable if the characteristic equation has real coefficients, complex ternrivS or exponential functions of s.
2. The criterion can be applied to any stability boundaries in complex plane, such as the unit circle in the z-plane.
3. The number of changes of signs in the elements of the first column equals the number of roots with negative real parts.
Which of these statements is/are not correct?
1. It is applicable if the characteristic equation has real coefficients, complex ternrivS or exponential functions of s.
2. The criterion can be applied to any stability boundaries in complex plane, such as the unit circle in the z-plane.
3. The number of changes of signs in the elements of the first column equals the number of roots with negative real parts.
Which of these statements is/are not correct?
a)
2 and 3 oniy .
b)
1, 2 and 3
c)
1 only
d)
1 and 2 only
|
|
Athul Banerjee answered |
• Routh-Hurwitz criterion is not applicable if characteristic equation has coefficients which are exponential or complex.
• It is not applied in z-piane because z-piane having unit circle is the stability boundary of discrete-data system.
• Statement-3 is also false because no. of sign change in 1st column of Routh’s array indicates the number of roots with positive real part or roots lying in RH s-plane.
• It is not applied in z-piane because z-piane having unit circle is the stability boundary of discrete-data system.
• Statement-3 is also false because no. of sign change in 1st column of Routh’s array indicates the number of roots with positive real part or roots lying in RH s-plane.
The characteristic equation of a second order discrete-data system is given by:
F(z) = z2+ z+ 0.25 = 0
The above system is- a)stable
- b)marginally stable
- c)unstable
- d)asymptotically stable
Correct answer is option 'A'. Can you explain this answer?
The characteristic equation of a second order discrete-data system is given by:
F(z) = z2+ z+ 0.25 = 0
The above system is
F(z) = z2+ z+ 0.25 = 0
The above system is
a)
stable
b)
marginally stable
c)
unstable
d)
asymptotically stable
|
|
Nilesh Joshi answered |
For a second order discrete- data system given by:
F(z) = a2z2 + a1z + a0 = 0
to be stable, the necessary and sufficient conditions are:
F(1) > 0
F(-1) > 0 and |a0| < a2
Here, F(z) = z2 + z + 0.25
So, = 0.25, a1 = 1, a2 = 1
Thus, F(1) - 12+ 1 + 0.25 = 2.25 > 0
F(-1) = 1 -1 + 0.25 = 0.25 > 0
and la0l = 0.25 < a2 = 1 Since ail the conditions are satisfied, therefore given system is stable.
F(z) = a2z2 + a1z + a0 = 0
to be stable, the necessary and sufficient conditions are:
F(1) > 0
F(-1) > 0 and |a0| < a2
Here, F(z) = z2 + z + 0.25
So, = 0.25, a1 = 1, a2 = 1
Thus, F(1) - 12+ 1 + 0.25 = 2.25 > 0
F(-1) = 1 -1 + 0.25 = 0.25 > 0
and la0l = 0.25 < a2 = 1 Since ail the conditions are satisfied, therefore given system is stable.
What is the stability of the system s3 + s2 + s + 4 = 0 using Hurwitz criteria?- a)Unstable
- b)Stable
- c)Critically stable
- d)Marginally stable
Correct answer is option 'A'. Can you explain this answer?
What is the stability of the system s3 + s2 + s + 4 = 0 using Hurwitz criteria?
a)
Unstable
b)
Stable
c)
Critically stable
d)
Marginally stable

|
Engineers Adda answered |
Concept:
To find the closed system stability by using RH criteria we require a characteristic equation.
Whereas in remaining all stability techniques we require open-loop transfer function.
The nth order general form of CE is a0 sn + a1 sn-1 + a2sn-2 + __________an-1 s1 +
an RH table shown below:


Necessary condition
All the coefficients of the characteristic equation should be positive and real.
Sufficient Conditions for stability:
1. All the coefficients in the first column should have the same sign and no coefficient should be zero.
2. If any sign changes in the first column, the system is unstable. And the number of sign changes = Number of poles in right of s-plane.
Calculation:
With the help of the
Routh table explained in the concept we can extend the calculation.
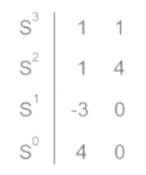
So in the first column, there are two sign changes, the system is unstable
Routh Hurwitz criterion is used to determine- a)peak response of the system
- b)time response of the system
- c)absolute stability of the system
- d)roots of the characteristic equation graphically
Correct answer is option 'C'. Can you explain this answer?
Routh Hurwitz criterion is used to determine
a)
peak response of the system
b)
time response of the system
c)
absolute stability of the system
d)
roots of the characteristic equation graphically

|
Engineers Adda answered |
Routh-Hurwitz criterion:
- Using the Routh-Hurwitz method, the stability information can be obtained without the need to solve the closed-loop system poles. This can be achieved by determining the number of poles that are in the left-half or right-half plane and on the imaginary axis.
- This involves checking the roots of the characteristic polynomial of a linear system to determine its stability.
- It is used to determine the absolute stability of a system.
Important points
Other methods of determining stability include:
Root locus:
- This method gives the position of the roots of the characteristic equation as the gain K is varied.
- With Root locus (unlike the case with Routh-Hurwitz criterion), we can do both analysis (i.e., for each gain value we know where the closed-loop poles are) and design (i.e., on the curve we can search for a gain value that results in the desired closed-loop poles).
Nyquist plot:
- This method is mainly used for assessing the stability of a system with feedback.
- While Nyquist is a graphical technique, it only provides a limited amount of intuition for why a system is stable or unstable, or how to modify an unstable system to be stable.
Techniques like Bode plots, while less general, are sometimes a more useful design tool.
The characteristic equation of a system is given by s3 + s + 2 - 0.What are the number of roots in the right half s-plane and on the jω-axis respectively?- a)3, 0
- b)2, 1
- c)1,2
- d)2,0
Correct answer is option 'D'. Can you explain this answer?
The characteristic equation of a system is given by s3 + s + 2 - 0.
What are the number of roots in the right half s-plane and on the jω-axis respectively?
a)
3, 0
b)
2, 1
c)
1,2
d)
2,0
|
|
Manisha Rane answered |
The characteristic equation of the system is given by:
s^3 + s + 2 = 0
To determine the number of roots in the right half s-plane, we need to evaluate the real parts of the roots. Since the equation is a third-degree polynomial, it can have up to three roots.
To find the roots, we can use the Routh-Hurwitz stability criterion. This method involves creating a Routh array using the coefficients of the characteristic equation:
1 2
1 0
2
To determine the number of roots in the right half s-plane, we count the number of sign changes in the first column of the Routh array. In this case, there is one sign change (from 1 to 2), so there is one root in the right half s-plane.
To determine the number of roots on the jω-axis, we count the number of sign changes in the first column of the Routh array after substituting jω for s. In this case, there are no sign changes, so there are no roots on the jω-axis.
s^3 + s + 2 = 0
To determine the number of roots in the right half s-plane, we need to evaluate the real parts of the roots. Since the equation is a third-degree polynomial, it can have up to three roots.
To find the roots, we can use the Routh-Hurwitz stability criterion. This method involves creating a Routh array using the coefficients of the characteristic equation:
1 2
1 0
2
To determine the number of roots in the right half s-plane, we count the number of sign changes in the first column of the Routh array. In this case, there is one sign change (from 1 to 2), so there is one root in the right half s-plane.
To determine the number of roots on the jω-axis, we count the number of sign changes in the first column of the Routh array after substituting jω for s. In this case, there are no sign changes, so there are no roots on the jω-axis.
The characteristic polynomial of a linear system is given as s4 + 3s3 + 5s2 + 6s + K + 10 = 0. What should be the condition on K so that the system is stable?- a)-10 < K < -4
- b)K > 10
- c)K > -4
- d)K > -10
Correct answer is option 'A'. Can you explain this answer?
The characteristic polynomial of a linear system is given as s4 + 3s3 + 5s2 + 6s + K + 10 = 0. What should be the condition on K so that the system is stable?
a)
-10 < K < -4
b)
K > 10
c)
K > -4
d)
K > -10

|
Engineers Adda answered |
Concept:
The characteristic equation for a given open-loop transfer function G(s) is
1 + G(s) H(s) = 0
To find the closed system stability by using RH criteria we require a characteristic equation. Whereas in remaining all stability techniques we require open-loop transfer function.
The nth order general form of CE is

RH table shown below:

Necessary condition: All the coefficients of the characteristic equation should be positive and real.
Sufficient Conditions for stability:
1. All the coefficients in the first column should have the same sign and no coefficient should be zero.
2. If any sign changes in the first column, the system is unstable.
And the number of sign changes = Number of poles in right of s-plane.
Calculation:
Characteristic equation: s4 + 3s3 + 5s2 + 6s + K + 10 = 0
By applying Routh tabulation method,
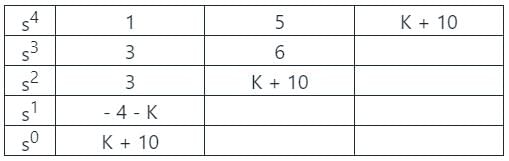
The system to become stable, the sign changes in the first column of the Routh table must be zero.
- 4 - K > 0 and K + 10 > 0
4 + K < 0 and K + 10 > 0
K < - 4 and K > - 10
⇒ - 10 < K < - 4
In the formation of Routh-Hurwitz array for a polynomial, all the elements of a row have zero values. This premature termination of the array indicates the presence of1. a pair of real roots with opposite sign2. complex conjugate roots on the imaginary axis3. a pair of complex conjugate roots with opposite real partsWhich of the above statements are correct?- a)Only 2
- b)2 and 3
- c)Only 3
- d)1, 2 and 3
Correct answer is option 'D'. Can you explain this answer?
In the formation of Routh-Hurwitz array for a polynomial, all the elements of a row have zero values. This premature termination of the array indicates the presence of
1. a pair of real roots with opposite sign
2. complex conjugate roots on the imaginary axis
3. a pair of complex conjugate roots with opposite real parts
Which of the above statements are correct?
a)
Only 2
b)
2 and 3
c)
Only 3
d)
1, 2 and 3
|
|
Hrishikesh Yadav answered |
Real roots with opposite sign:
- When all elements of a row in the Routh-Hurwitz array are zero, it indicates that the corresponding polynomial has a pair of real roots with opposite signs.
- This means that the polynomial has one root with a positive value and the other root with a negative value.
Complex conjugate roots on the imaginary axis:
- If the entire row in the Routh-Hurwitz array is zero, it does not indicate the presence of complex conjugate roots on the imaginary axis.
- The premature termination of the array does not provide information about the location of complex roots on the imaginary axis.
Complex conjugate roots with opposite real parts:
- The presence of a pair of complex conjugate roots with opposite real parts can be inferred from the premature termination of the Routh-Hurwitz array.
- This situation occurs when all elements of a row in the array are zero, suggesting the existence of complex roots with opposite real parts.
Therefore, the correct answer is option 'D', which includes all three statements. The Routh-Hurwitz array can provide valuable information about the nature and location of roots of a polynomial, helping in analyzing the stability of a system in control theory.
- When all elements of a row in the Routh-Hurwitz array are zero, it indicates that the corresponding polynomial has a pair of real roots with opposite signs.
- This means that the polynomial has one root with a positive value and the other root with a negative value.
Complex conjugate roots on the imaginary axis:
- If the entire row in the Routh-Hurwitz array is zero, it does not indicate the presence of complex conjugate roots on the imaginary axis.
- The premature termination of the array does not provide information about the location of complex roots on the imaginary axis.
Complex conjugate roots with opposite real parts:
- The presence of a pair of complex conjugate roots with opposite real parts can be inferred from the premature termination of the Routh-Hurwitz array.
- This situation occurs when all elements of a row in the array are zero, suggesting the existence of complex roots with opposite real parts.
Therefore, the correct answer is option 'D', which includes all three statements. The Routh-Hurwitz array can provide valuable information about the nature and location of roots of a polynomial, helping in analyzing the stability of a system in control theory.
Which of the following is the correct comment on stability based on unknown k for the feedback system with characteristic s4 + 2ks3 + s2 + 5s + 5 = 0?- a)Unstable for all the values of k
- b)Stable for zero value of k
- c)Stable for positive value of k
- d)Stable for all the values of k
Correct answer is option 'A'. Can you explain this answer?
Which of the following is the correct comment on stability based on unknown k for the feedback system with characteristic s4 + 2ks3 + s2 + 5s + 5 = 0?
a)
Unstable for all the values of k
b)
Stable for zero value of k
c)
Stable for positive value of k
d)
Stable for all the values of k

|
Engineers Adda answered |
Concept:
The characteristic equation for a given open-loop transfer function G(s) is
1 + G(s) H(s) = 0
According to the Routh tabulation method,
The system is said to be stable if there are no sign changes in the first column of Routh array
The number of poles lie on the right half of s plane = number of sign changes
Calculation:
Characteristic equation: s4 + 2ks3 + s2 + 5s + 5 = 0
By applying the Routh tabulation method,
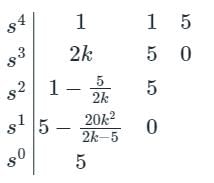
The system to become stable, the sign changes in the first column of Routh table must be zero.
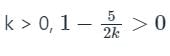
⇒ k > 2.5
For all the values of 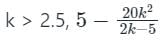 gives negative values.
gives negative values.
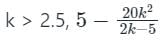 gives negative values.
gives negative values.Therefore, the given system is unstable for all the values of k.
Assertion (A): For a system to be stable, the roots of the characteristic equation should not lie in the right half of the s-plane or on the imaginary axis.
Reason (R): A system is said to be stable if the zeros of the closed loop transfer function are all in the left half of s-plane.- a)Both A and R are true and R is a correct explanation of A.
- b)Both A and R are true but R is not a correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'C'. Can you explain this answer?
Assertion (A): For a system to be stable, the roots of the characteristic equation should not lie in the right half of the s-plane or on the imaginary axis.
Reason (R): A system is said to be stable if the zeros of the closed loop transfer function are all in the left half of s-plane.
Reason (R): A system is said to be stable if the zeros of the closed loop transfer function are all in the left half of s-plane.
a)
Both A and R are true and R is a correct explanation of A.
b)
Both A and R are true but R is not a correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Rajat Kumar answered |
Poles of the closed loop transfer function is the characteristic equation of a closed loop control system. For the system to be stable all roots of characteristic equation should lie in LH s-plane. Hence reason is false.
For a discrete-time system to be unstable, all the poles of the z-transfer function should lie- a)on the left-half of z-plane
- b)on the right-half of z-plane
- c)outside the circle of unit radius
- d)within a circle of unit radius
Correct answer is option 'C'. Can you explain this answer?
For a discrete-time system to be unstable, all the poles of the z-transfer function should lie
a)
on the left-half of z-plane
b)
on the right-half of z-plane
c)
outside the circle of unit radius
d)
within a circle of unit radius
|
|
Mihir Chawla answered |
Assertion (A): A system is said to be stable if the impulse response approaches zero for sufficiently large time.
Reason (R): If the impulse response approaches infinity for sufficiently large time, the system is said to be unstable- a)Both A and R are true and R is a correct explanation of A.
- b)Both A and R are true but R is not a correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'B'. Can you explain this answer?
Assertion (A): A system is said to be stable if the impulse response approaches zero for sufficiently large time.
Reason (R): If the impulse response approaches infinity for sufficiently large time, the system is said to be unstable
Reason (R): If the impulse response approaches infinity for sufficiently large time, the system is said to be unstable
a)
Both A and R are true and R is a correct explanation of A.
b)
Both A and R are true but R is not a correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Sravya Bajaj answered |
Both assertion and reason are individually true. The correct reason for assertion is BIBO stability criteria,
Assertion (A): If the system is stable we can determine the relative stability by the settling time of the system.
Reason (R): If the settling time is less than that of the other system then the system is said to be relatively more stable.- a)Both A and R are true and R is a correct explanation of A.
- b)Both A and R are true but R is not a correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'A'. Can you explain this answer?
Assertion (A): If the system is stable we can determine the relative stability by the settling time of the system.
Reason (R): If the settling time is less than that of the other system then the system is said to be relatively more stable.
Reason (R): If the settling time is less than that of the other system then the system is said to be relatively more stable.
a)
Both A and R are true and R is a correct explanation of A.
b)
Both A and R are true but R is not a correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Shalini Banerjee answered |
The settling time is inversely proportional to the real part of the dominant roots. If the settling time is less compared to other system, then the system will be relatively more stable
Consider the following characteristic equation of a system:
s3 + 2Ks2 + (K+ 2) s+ 4 = 0
Which one of the following is correct?- a)The system is stable for all positive values of K.
- b)The system is unstable for all values of K.
- c)The system is stable for values of K > 0.73.
- d)The system is stable for value of K < 0.73.
Correct answer is option 'C'. Can you explain this answer?
Consider the following characteristic equation of a system:
s3 + 2Ks2 + (K+ 2) s+ 4 = 0
Which one of the following is correct?
s3 + 2Ks2 + (K+ 2) s+ 4 = 0
Which one of the following is correct?
a)
The system is stable for all positive values of K.
b)
The system is unstable for all values of K.
c)
The system is stable for values of K > 0.73.
d)
The system is stable for value of K < 0.73.
|
|
Sandeep Saha answered |
Given characteristic equation is,
s2 + 2Ks2 + (K + 2)s + 4 = 0
Routh’s array is:
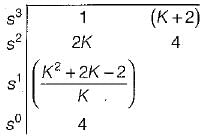
For stability, 2K > 0 or K > 0
Also,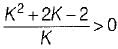 or K2 + 2 K - 2 > 0
or K2 + 2 K - 2 > 0
Now, K2 + 2K - 2 = 0 or, K = 0.73, -2.73 For K > 0.73, K2 + 2 K - 2 > 0
(since K should be > 0)
Hence, system will be stable if K > 0.73.
s2 + 2Ks2 + (K + 2)s + 4 = 0
Routh’s array is:

For stability, 2K > 0 or K > 0
Also,
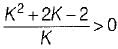 or K2 + 2 K - 2 > 0
or K2 + 2 K - 2 > 0Now, K2 + 2K - 2 = 0 or, K = 0.73, -2.73 For K > 0.73, K2 + 2 K - 2 > 0
(since K should be > 0)
Hence, system will be stable if K > 0.73.
The number of sign changes in the Routh’s array indicates the number of roots lying in the- a)origin of s-plane
- b)left half of s-plane
- c)right half of s-piane
- d)centre of the s-plane
Correct answer is option 'C'. Can you explain this answer?
The number of sign changes in the Routh’s array indicates the number of roots lying in the
a)
origin of s-plane
b)
left half of s-plane
c)
right half of s-piane
d)
centre of the s-plane
|
|
Om Choudhury answered |
Number of sign changes in the first column of Routh’s array indicates the number of closed loop poles or roots of characteristic equation lying in the right half of s-plane.
For the system shown in fig. the number of poles on RHP, LHP, and imaginary axis are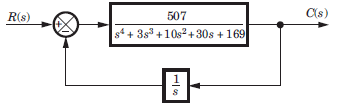
- a)2, 3, 0
- b)3, 2, 0
- c)2, 1, 2
- d)1, 2, 2
Correct answer is option 'D'. Can you explain this answer?
For the system shown in fig. the number of poles on RHP, LHP, and imaginary axis are
a)
2, 3, 0
b)
3, 2, 0
c)
2, 1, 2
d)
1, 2, 2
|
|
Shraddha Yadav answered |
Closed loop transfer function
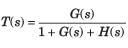
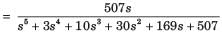
Routh table is as shown in fig. S.6.2.34
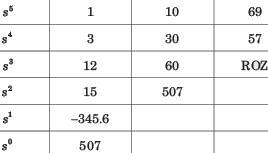

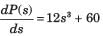
From s4 row down to s0 there is one sign change. So LHP–1 + 1= 2 pole. RHP–1 pole, jw - axis - 2 pole.
Which among these is a classification of power system stability?- a)Frequency stability
- b)Voltage stability
- c)Rotor angle stability
- d)All of these
Correct answer is option 'D'. Can you explain this answer?
Which among these is a classification of power system stability?
a)
Frequency stability
b)
Voltage stability
c)
Rotor angle stability
d)
All of these
|
|
Tarun Sen answered |
**Classification of Power System Stability**
Power system stability refers to the ability of a power system to maintain a steady, synchronized operation under normal and abnormal conditions. It is crucial for the reliable and efficient operation of the electrical grid. Power system stability can be classified into three main categories:
**1. Frequency Stability:**
Frequency stability refers to the ability of a power system to maintain a stable frequency during normal and abnormal operating conditions. The frequency of an electrical system is determined by the balance between the generation and consumption of electrical power. Any imbalance between generation and load can cause frequency deviations.
**2. Voltage Stability:**
Voltage stability refers to the ability of a power system to maintain a stable voltage profile under normal and abnormal conditions. Voltage fluctuations can lead to equipment malfunctions, damage to electrical devices, and disruption of power supply. Voltage stability is influenced by factors such as load variations, reactive power demand, and system configuration.
**3. Rotor Angle Stability:**
Rotor angle stability, also known as transient stability, refers to the ability of a power system to maintain synchronism and restore stability after a disturbance. It specifically focuses on the stability of the synchronous machines in the power system. Rotor angle stability is critical for maintaining the overall stability of the power system and preventing cascading failures.
**Why the correct answer is option 'D':**
The correct answer is option 'D' - All of these because frequency stability, voltage stability, and rotor angle stability are all different aspects of power system stability. Each aspect addresses a specific characteristic and stability concern of the power system. These three classifications are interrelated and collectively contribute to the overall stability and reliability of the power system.
Frequency stability ensures that the system frequency remains within acceptable limits, preventing excessive speed changes in synchronous generators. Voltage stability ensures that the system voltage remains within acceptable limits, preventing voltage collapse and blackouts. Rotor angle stability ensures that the synchronous generators maintain synchronism and remain stable after disturbances, preventing cascading failures.
Therefore, all three classifications of power system stability - frequency stability, voltage stability, and rotor angle stability - are essential for the reliable operation of the electrical grid and the prevention of power system failures.
Power system stability refers to the ability of a power system to maintain a steady, synchronized operation under normal and abnormal conditions. It is crucial for the reliable and efficient operation of the electrical grid. Power system stability can be classified into three main categories:
**1. Frequency Stability:**
Frequency stability refers to the ability of a power system to maintain a stable frequency during normal and abnormal operating conditions. The frequency of an electrical system is determined by the balance between the generation and consumption of electrical power. Any imbalance between generation and load can cause frequency deviations.
**2. Voltage Stability:**
Voltage stability refers to the ability of a power system to maintain a stable voltage profile under normal and abnormal conditions. Voltage fluctuations can lead to equipment malfunctions, damage to electrical devices, and disruption of power supply. Voltage stability is influenced by factors such as load variations, reactive power demand, and system configuration.
**3. Rotor Angle Stability:**
Rotor angle stability, also known as transient stability, refers to the ability of a power system to maintain synchronism and restore stability after a disturbance. It specifically focuses on the stability of the synchronous machines in the power system. Rotor angle stability is critical for maintaining the overall stability of the power system and preventing cascading failures.
**Why the correct answer is option 'D':**
The correct answer is option 'D' - All of these because frequency stability, voltage stability, and rotor angle stability are all different aspects of power system stability. Each aspect addresses a specific characteristic and stability concern of the power system. These three classifications are interrelated and collectively contribute to the overall stability and reliability of the power system.
Frequency stability ensures that the system frequency remains within acceptable limits, preventing excessive speed changes in synchronous generators. Voltage stability ensures that the system voltage remains within acceptable limits, preventing voltage collapse and blackouts. Rotor angle stability ensures that the synchronous generators maintain synchronism and remain stable after disturbances, preventing cascading failures.
Therefore, all three classifications of power system stability - frequency stability, voltage stability, and rotor angle stability - are essential for the reliable operation of the electrical grid and the prevention of power system failures.
A closed loop system has the characteristic equation given by s3 + Ks2 + (K + 2)s + 3 = 0. For this system to be stable, which one of the following conditions should be satisfied?- a)0 < K < 0.5
- b)0.5 < K < 1
- c)0 < K < 1
- d)K > 1
Correct answer is option 'D'. Can you explain this answer?
A closed loop system has the characteristic equation given by s3 + Ks2 + (K + 2)s + 3 = 0. For this system to be stable, which one of the following conditions should be satisfied?
a)
0 < K < 0.5
b)
0.5 < K < 1
c)
0 < K < 1
d)
K > 1

|
Vertex Academy answered |
Given that characteristic equation is,
s3 + Ks2 + (K + 2)s + 3 = 0
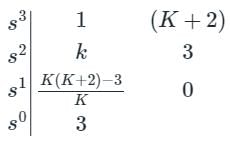
For system to be stable,
K > 0, K (K + 2) - 3 > 0
⇒ K > 0, K2 + 2K - 3 > 0
⇒ K > 0, (K + 3) (K - 1) > 0
⇒ K > 0, K > -3, K > 1 ⇒ K > 1
If the roots have negative real parts, then the response is ____________ - a)Stable
- b)Bounded
- c)Unstable
- d)Marginally stable
Correct answer is option 'B'. Can you explain this answer?
If the roots have negative real parts, then the response is ____________
a)
Stable
b)
Bounded
c)
Unstable
d)
Marginally stable
|
|
Bhavya Singh answered |
Understanding System Stability
In control theory, the stability of a system is determined by the behavior of its roots, often referred to as poles, in the system's characteristic equation. The nature of these roots significantly impacts the system's response.
Roots with Negative Real Parts
- When the roots of the characteristic equation have negative real parts, it indicates that the system is capable of returning to equilibrium after a disturbance.
- This typically results in a response that decays over time, leading to a stable system.
Response Types
1. Stable Response:
- Systems with all roots having negative real parts are classified as stable.
- This means that any perturbation will die out over time, and the system will settle at a steady state.
2. Bounded Response:
- A bounded response implies that the system's output remains within fixed limits over time.
- While a bounded response can be observed in some stable systems, it does not necessarily indicate stability as it can also apply to marginally stable systems.
3. Unstable Response:
- Systems with at least one root having a positive real part lead to an unstable response where outputs can grow indefinitely.
4. Marginally Stable:
- A system is considered marginally stable if it has roots on the imaginary axis.
- These systems oscillate indefinitely without growing or decaying.
Conclusion
Given that the roots have negative real parts, the correct classification of the response is Stable. Therefore, the assertion that the response is bounded is misleading. The correct answer should be a) Stable, not b) Bounded.
In control theory, the stability of a system is determined by the behavior of its roots, often referred to as poles, in the system's characteristic equation. The nature of these roots significantly impacts the system's response.
Roots with Negative Real Parts
- When the roots of the characteristic equation have negative real parts, it indicates that the system is capable of returning to equilibrium after a disturbance.
- This typically results in a response that decays over time, leading to a stable system.
Response Types
1. Stable Response:
- Systems with all roots having negative real parts are classified as stable.
- This means that any perturbation will die out over time, and the system will settle at a steady state.
2. Bounded Response:
- A bounded response implies that the system's output remains within fixed limits over time.
- While a bounded response can be observed in some stable systems, it does not necessarily indicate stability as it can also apply to marginally stable systems.
3. Unstable Response:
- Systems with at least one root having a positive real part lead to an unstable response where outputs can grow indefinitely.
4. Marginally Stable:
- A system is considered marginally stable if it has roots on the imaginary axis.
- These systems oscillate indefinitely without growing or decaying.
Conclusion
Given that the roots have negative real parts, the correct classification of the response is Stable. Therefore, the assertion that the response is bounded is misleading. The correct answer should be a) Stable, not b) Bounded.
The z-transform of a sianal is aiven by:
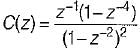
Its final value is- a)1/4
- b)zero
- c)-1
- d)infinity
Correct answer is option 'C'. Can you explain this answer?
The z-transform of a sianal is aiven by:
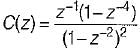
Its final value is
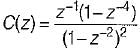
Its final value is
a)
1/4
b)
zero
c)
-1
d)
infinity
|
|
Aditya Basu answered |
Given, 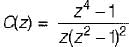
Applying final value theorem,
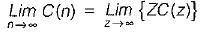
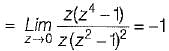
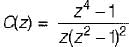
Applying final value theorem,
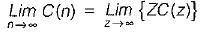
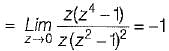
The characteristic equation of given system is 6s + K = 0. Determined the range of K for which the system to be stable.- a)0 < K
- b)0 < K ≤ 6
- c)0 < K < 1/6
- d)6 < K ≤ 60
Correct answer is option 'A'. Can you explain this answer?
The characteristic equation of given system is 6s + K = 0. Determined the range of K for which the system to be stable.
a)
0 < K
b)
0 < K ≤ 6
c)
0 < K < 1/6
d)
6 < K ≤ 60
|
|
Ashutosh Majumdar answered |
Characteristic Equation Analysis
The characteristic equation of a system is given by:
6s + K = 0
To determine stability, we analyze the roots of this equation. The system is stable if all poles have negative real parts.
Finding the Roots
To find the roots, solve for 's':
s = -K/6
This indicates that the pole of the system is located at -K/6 on the s-plane.
Stability Condition
For the system to be stable, we require:
-K/6 < 0="" this="" implies:="" -k="" />< 0="" thus,="" k="" /> 0
Range of K for Stability
From our analysis, we conclude that:
- The system will be stable as long as K is greater than 0.
- If K <= 0,="" the="" pole="" will="" either="" lie="" on="" the="" imaginary="" axis="" (k="0)" or="" in="" the="" right="" half="" of="" the="" s-plane="" (k="">< 0),="" leading="" to="" instability.="" />Conclusion
Thus, the range of K for which the system is stable is:
0 < />
This corresponds to option A. K must be positive to ensure that the pole remains in the left half of the s-plane, ensuring stability. k="" this="" corresponds="" to="" option="" a.="" k="" must="" be="" positive="" to="" ensure="" that="" the="" pole="" remains="" in="" the="" left="" half="" of="" the="" s-plane,="" ensuring="">
This corresponds to option A. K must be positive to ensure that the pole remains in the left half of the s-plane, ensuring stability.>
The characteristic equation of a system is given by:
6s + K = 0
To determine stability, we analyze the roots of this equation. The system is stable if all poles have negative real parts.
Finding the Roots
To find the roots, solve for 's':
s = -K/6
This indicates that the pole of the system is located at -K/6 on the s-plane.
Stability Condition
For the system to be stable, we require:
-K/6 < 0="" this="" implies:="" -k="" />< 0="" thus,="" k="" /> 0
Range of K for Stability
From our analysis, we conclude that:
- The system will be stable as long as K is greater than 0.
- If K <= 0,="" the="" pole="" will="" either="" lie="" on="" the="" imaginary="" axis="" (k="0)" or="" in="" the="" right="" half="" of="" the="" s-plane="" (k="">< 0),="" leading="" to="" instability.="" />Conclusion
Thus, the range of K for which the system is stable is:
0 < />
This corresponds to option A. K must be positive to ensure that the pole remains in the left half of the s-plane, ensuring stability. k="" this="" corresponds="" to="" option="" a.="" k="" must="" be="" positive="" to="" ensure="" that="" the="" pole="" remains="" in="" the="" left="" half="" of="" the="" s-plane,="" ensuring="">
This corresponds to option A. K must be positive to ensure that the pole remains in the left half of the s-plane, ensuring stability.>
Given the following polynomial equations3 + 5.5s2 + 8.5s + 3 = 0the number of roots of the polynomial, which have real parts strictly less than −1, is ________ Correct answer is '2'. Can you explain this answer?
Given the following polynomial equation
s3 + 5.5s2 + 8.5s + 3 = 0
the number of roots of the polynomial, which have real parts strictly less than −1, is ________

|
Engineers Adda answered |
s3 + 5.5s2 + 8.5s + 3 = 0
Putting s = z -1
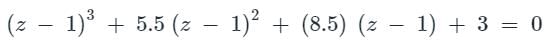
z3 + 2.5z2 + 0.5z - 1 = 1
Taking routh criteria for the given characteristic equation

As there is one sign change hence, two roots of given polynomial will lie to the left of s = -1.

As there is one sign change hence, two roots of given polynomial will lie to the left of s = -1.
The characteristic equation of a feedback system is s3 + Ks2 + 5s + 10 = 0. For a stable system, the value of K should not be less than- a)1
- b)2
- c)3
- d)4.5
Correct answer is option 'B'. Can you explain this answer?
The characteristic equation of a feedback system is s3 + Ks2 + 5s + 10 = 0. For a stable system, the value of K should not be less than
a)
1
b)
2
c)
3
d)
4.5

|
EduRev GATE answered |
Concept:
The characteristic equation for a given open-loop transfer function G(s) is
1 + G(s) H(s) = 0
To find the closed system stability by using RH criteria we require a characteristic equation. Whereas in remaining all stability techniques we require open-loop transfer function.
The nth order general form of CE is
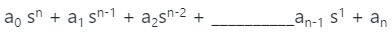
RH table shown below:

Necessary condition: All the coefficients of the characteristic equation should be positive and real.
Sufficient Conditions for stability:
1. All the coefficients in the first column should have the same sign and no coefficient should be zero.
2. If any sign changes in the first column, the system is unstable.
And the number of sign changes = Number of poles in right of s-plane.
Calculation:
Characteristic equation: s3 + Ks2 + 5s + 10 = 0
By applying Routh tabulation method,
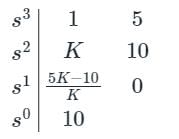
The system to become stable, the sign changes in the first column of the Routh table must be zero.
5K – 10 > 0 and K > 0
⇒ K > 2
The characteristic ecjuation of a linear tirne-invariant discrete-data system is given by:
F(z) = anzn + an - 1 zn - 1 + .......... + a1 z + a0 = 0
where all the coefficients are real.
According to “Jury’s stability criterion”, there are certain necessary conditions which must be satisfied for the above discrete-data system to have no roots on or outside the unit circle. Which of the following necessary condition does not holds true for the discrete-data system to have all roots inside the unit circle according to “Jury's stability criterion"?- a)|a0| > |an|
- b)F (1) > 0
- c)F(-1) > 0 (if n = even integer)
- d)F(-1) < 0 (if n = odd integer)
Correct answer is option 'A'. Can you explain this answer?
The characteristic ecjuation of a linear tirne-invariant discrete-data system is given by:
F(z) = anzn + an - 1 zn - 1 + .......... + a1 z + a0 = 0
where all the coefficients are real.
According to “Jury’s stability criterion”, there are certain necessary conditions which must be satisfied for the above discrete-data system to have no roots on or outside the unit circle. Which of the following necessary condition does not holds true for the discrete-data system to have all roots inside the unit circle according to “Jury's stability criterion"?
F(z) = anzn + an - 1 zn - 1 + .......... + a1 z + a0 = 0
where all the coefficients are real.
According to “Jury’s stability criterion”, there are certain necessary conditions which must be satisfied for the above discrete-data system to have no roots on or outside the unit circle. Which of the following necessary condition does not holds true for the discrete-data system to have all roots inside the unit circle according to “Jury's stability criterion"?
a)
|a0| > |an|
b)
F (1) > 0
c)
F(-1) > 0 (if n = even integer)
d)
F(-1) < 0 (if n = odd integer)
|
|
Srestha Gupta answered |
The necessary conditions for stability are: F (1) > 0
F(-1) > 0, if n = even integer
F(-1) < 0, if n = odd integer
and |a0| < |an|
F(-1) > 0, if n = even integer
F(-1) < 0, if n = odd integer
and |a0| < |an|
The number of roots of s3 + 5s2 + 7s + 3 = 0 in the left half of the s-plane is- a)zero
- b)one
- c)two
- d)three
Correct answer is option 'D'. Can you explain this answer?
The number of roots of s3 + 5s2 + 7s + 3 = 0 in the left half of the s-plane is
a)
zero
b)
one
c)
two
d)
three
|
|
Saranya Mishra answered |
Understanding the Polynomial
The given polynomial is:
s³ + 5s² + 7s + 3 = 0
To find the number of roots in the left half of the s-plane, we can apply the Routh-Hurwitz criterion.
Applying Routh-Hurwitz Criterion
The Routh-Hurwitz criterion provides a systematic way to determine the stability of a system by analyzing the coefficients of the characteristic polynomial.
1. Construct the Routh Array:
- The first row consists of the coefficients of s³ and s¹: (1, 7)
- The second row consists of the coefficients of s² and s⁰: (5, 3)
The Routh array will look like this:
| s³ | 1 | 7 |
|----|----|----|
| s² | 5 | 3 |
| s¹ | | |
| s⁰ | | |
2. Calculate the Remaining Rows:
- For s¹: (5*7 - 3*1) / 5 = 33/5
- For s⁰: 3
The updated Routh array now is:
| s³ | 1 | 7 |
|----|------|-----|
| s² | 5 | 3 |
| s¹ | 33/5 | 0 |
| s⁰ | 3 | 0 |
3. Count Sign Changes:
- All elements in the first column (1, 5, 33/5, 3) are positive. Therefore, there are no sign changes.
Conclusion
Since there are no sign changes in the first column of the Routh array, the polynomial has 3 roots in the left half of the s-plane. Thus, the correct answer is:
Option D: Three roots
The given polynomial is:
s³ + 5s² + 7s + 3 = 0
To find the number of roots in the left half of the s-plane, we can apply the Routh-Hurwitz criterion.
Applying Routh-Hurwitz Criterion
The Routh-Hurwitz criterion provides a systematic way to determine the stability of a system by analyzing the coefficients of the characteristic polynomial.
1. Construct the Routh Array:
- The first row consists of the coefficients of s³ and s¹: (1, 7)
- The second row consists of the coefficients of s² and s⁰: (5, 3)
The Routh array will look like this:
| s³ | 1 | 7 |
|----|----|----|
| s² | 5 | 3 |
| s¹ | | |
| s⁰ | | |
2. Calculate the Remaining Rows:
- For s¹: (5*7 - 3*1) / 5 = 33/5
- For s⁰: 3
The updated Routh array now is:
| s³ | 1 | 7 |
|----|------|-----|
| s² | 5 | 3 |
| s¹ | 33/5 | 0 |
| s⁰ | 3 | 0 |
3. Count Sign Changes:
- All elements in the first column (1, 5, 33/5, 3) are positive. Therefore, there are no sign changes.
Conclusion
Since there are no sign changes in the first column of the Routh array, the polynomial has 3 roots in the left half of the s-plane. Thus, the correct answer is:
Option D: Three roots
What is the range of values of K (K > 0) such that the characteristic equation
s3 + 3 (K+ 1)s2 + (7K+ 5)s + (4K + 7) = 0
has roots more negative than s = -1?- a)∞ > K > 0.53
- b)-2.5 < K < 0.53
- c)∞ > K > 0.25
- d)1 > K > 0.25
Correct answer is option 'A'. Can you explain this answer?
What is the range of values of K (K > 0) such that the characteristic equation
s3 + 3 (K+ 1)s2 + (7K+ 5)s + (4K + 7) = 0
has roots more negative than s = -1?
s3 + 3 (K+ 1)s2 + (7K+ 5)s + (4K + 7) = 0
has roots more negative than s = -1?
a)
∞ > K > 0.53
b)
-2.5 < K < 0.53
c)
∞ > K > 0.25
d)
1 > K > 0.25
|
|
Shivam Ghosh answered |
Putting s = (z - 1) in the given characteristic equation, we get:
( z - 1)3 + 3 (K + 1) ( z - 1)2 + (7K+ 5) ( z - 1) + (4K + 7) = 0
or, z3 + 3 Kz2 + ( K + 2 )z + 4 = 0
Routh’s array is:

For stability,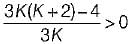 and 3 K > 0
and 3 K > 0
i.e. 3K2 + 6K - 4 > 0 and K > 0
Now, roots of 3K2 + 6K~4 = 0 are: K = -2.5, 0.53
Since K > 0 ∴ K = 0.53 (K = -2.5 neglected)
For K > 0.53, 3 K2 + 6 K - 4 > 0
Hence, the range of value of K is
0.53 < K < ∞ or ∞ > K > 0.53
( z - 1)3 + 3 (K + 1) ( z - 1)2 + (7K+ 5) ( z - 1) + (4K + 7) = 0
or, z3 + 3 Kz2 + ( K + 2 )z + 4 = 0
Routh’s array is:

For stability,
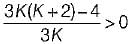 and 3 K > 0
and 3 K > 0i.e. 3K2 + 6K - 4 > 0 and K > 0
Now, roots of 3K2 + 6K~4 = 0 are: K = -2.5, 0.53
Since K > 0 ∴ K = 0.53 (K = -2.5 neglected)
For K > 0.53, 3 K2 + 6 K - 4 > 0
Hence, the range of value of K is
0.53 < K < ∞ or ∞ > K > 0.53
If the unit step response of a system is given by c(t) = -1.5 + et + 0.5e-2f, then the system will be- a)stable
- b)unstable
- c)relatively stable
- d)marginally stable
Correct answer is option 'B'. Can you explain this answer?
If the unit step response of a system is given by c(t) = -1.5 + et + 0.5e-2f, then the system will be
a)
stable
b)
unstable
c)
relatively stable
d)
marginally stable
|
|
Ankit Chauhan answered |
Given, step response:
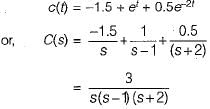
∴ Transfer function is
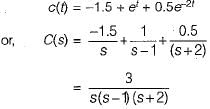
∴ Transfer function is
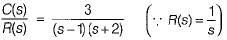
Since one of the closed loop pole (s = 1) lies in RH s-plane, therefore given system is unstable.
The forward path transfer of ufb system is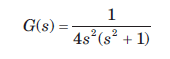 The system is
The system is- a)stable
- b)unstable
- c)marginally stable
- d)More information is required
Correct answer is option 'B'. Can you explain this answer?
The forward path transfer of ufb system is
The system is
a)
stable
b)
unstable
c)
marginally stable
d)
More information is required

|
muddam rajasekhar answered |
A system is stable all the coefficient of s must be present
The presence of non-linearities in a control system tends to introduce- a)instability
- b)steady state error
- c)transient error
- d)all of these
Correct answer is option 'D'. Can you explain this answer?
The presence of non-linearities in a control system tends to introduce
a)
instability
b)
steady state error
c)
transient error
d)
all of these
|
|
Avik Goyal answered |
Introduction:
A control system is a system that manages, commands, directs or regulates the behavior of other devices or systems. A control system can be linear or non-linear. Non-linear control systems are more complex than linear control systems. The presence of non-linearities in a control system tends to introduce instability, steady-state error, and transient error.
Instability:
Instability is a condition where the system output becomes unbounded or oscillatory when the input is bounded. Non-linearities in a control system can cause instability because they can amplify or dampen the system response. The amplification or damping effect depends on the operating point of the system. As the operating point changes, the amplification or damping effect can change, leading to instability.
Steady-state error:
Steady-state error is the error that exists between the desired output and the actual output when the system has reached a steady-state condition. Non-linearities in a control system can cause steady-state error because they can change the input-output relationship. The change in the input-output relationship can result in a deviation between the desired output and the actual output.
Transient error:
Transient error is the error that exists between the desired output and the actual output during the transient period. Non-linearities in a control system can cause transient error because they can affect the system response during the transient period. The effect of non-linearities on the system response during the transient period can result in a deviation between the desired output and the actual output.
Conclusion:
In conclusion, the presence of non-linearities in a control system tends to introduce instability, steady-state error, and transient error. These effects can make the control system more complex and difficult to manage. Therefore, it is important to consider the non-linearities in a control system and try to mitigate their effects.
A control system is a system that manages, commands, directs or regulates the behavior of other devices or systems. A control system can be linear or non-linear. Non-linear control systems are more complex than linear control systems. The presence of non-linearities in a control system tends to introduce instability, steady-state error, and transient error.
Instability:
Instability is a condition where the system output becomes unbounded or oscillatory when the input is bounded. Non-linearities in a control system can cause instability because they can amplify or dampen the system response. The amplification or damping effect depends on the operating point of the system. As the operating point changes, the amplification or damping effect can change, leading to instability.
Steady-state error:
Steady-state error is the error that exists between the desired output and the actual output when the system has reached a steady-state condition. Non-linearities in a control system can cause steady-state error because they can change the input-output relationship. The change in the input-output relationship can result in a deviation between the desired output and the actual output.
Transient error:
Transient error is the error that exists between the desired output and the actual output during the transient period. Non-linearities in a control system can cause transient error because they can affect the system response during the transient period. The effect of non-linearities on the system response during the transient period can result in a deviation between the desired output and the actual output.
Conclusion:
In conclusion, the presence of non-linearities in a control system tends to introduce instability, steady-state error, and transient error. These effects can make the control system more complex and difficult to manage. Therefore, it is important to consider the non-linearities in a control system and try to mitigate their effects.
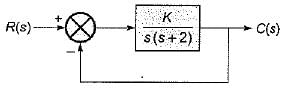
A closed loop control system is shown below:
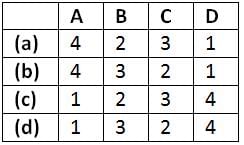
Match List - I (Different values of K) with List - II (Roots of Characteristic Equation) and select the correct answer using the codes given below the lists:

Codes:
- a)a
- b)b
- c)c
- d)d
Correct answer is option 'B'. Can you explain this answer?
A closed loop control system is shown below:

Match List - I (Different values of K) with List - II (Roots of Characteristic Equation) and select the correct answer using the codes given below the lists:

Codes:


Match List - I (Different values of K) with List - II (Roots of Characteristic Equation) and select the correct answer using the codes given below the lists:

Codes:

a)
a
b)
b
c)
c
d)
d
|
|
Mahesh Singh answered |
The characteristic equation is
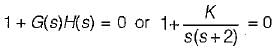
or, s2 + 2 s + K = 0
or,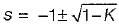
When, 0 < K < 1, roots are real and distinct. When, K = 0, roots are s = 0, -2 (Poles of open loopT.F. G(s)H(s)).
When, K = 1, roots are s = -1, -1 i.e. real and equal.
When, K > 1, roots are complex conjugate.
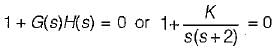
or, s2 + 2 s + K = 0
or,
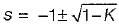
When, 0 < K < 1, roots are real and distinct. When, K = 0, roots are s = 0, -2 (Poles of open loopT.F. G(s)H(s)).
When, K = 1, roots are s = -1, -1 i.e. real and equal.
When, K > 1, roots are complex conjugate.
The forward-path transfer function of a ufb system is 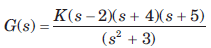 For system to be stable, the range of K is
For system to be stable, the range of K is- a)
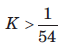
- b)
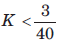
- c)
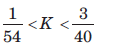
- d)unstable
Correct answer is option 'C'. Can you explain this answer?
The forward-path transfer function of a ufb system is
For system to be stable, the range of K is
a)
b)
c)
d)
unstable
|
|
Dipanjan Nair answered |

Routh table is as shown in fig. S.6.211


The closed loop transfer function for this system is
- a)

- b)

- c)

- d)

Correct answer is option 'B'. Can you explain this answer?
The closed loop transfer function for this system is

a)
b)
c)

d)

|
Diya Patel answered |
First combine the parallel loop K/s2
and 2/s giving
 Then apply feedback formula with
Then apply feedback formula with  and
and  and then multiply with s2.
and then multiply with s2.


and 2/s giving
 Then apply feedback formula with
Then apply feedback formula with  and
and  and then multiply with s2.
and then multiply with s2.

Find the range of k for stable operation if H(s) = 1 and G(s) 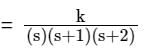
- a)0 < k < 3
- b)0 < k < 6
- c)0 < k < 12
- d)k > 6
Correct answer is option 'B'. Can you explain this answer?
Find the range of k for stable operation if H(s) = 1 and G(s) 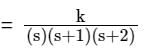
a)
0 < k < 3
b)
0 < k < 6
c)
0 < k < 12
d)
k > 6

|
EduRev GATE answered |
Concept:
- The characteristic equation for a given open-loop transfer function
- G(s) is 1 + G(s) H(s) = 0
- According to the Routh tabulation method, The system is said to be stable if there are no sign changes in the first column of the Routh array The number of poles lies on the right half of s plane = number of sign changes
Calculation:
Characteristic equation: s3 + 3s2 + 2s + k = 0 By applying the Routh tabulation method,
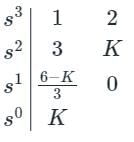
For the system to become stable, the sign changes in the first column of the Routh table must be zero.
6 - K > 0 and K > 0,
The range of k for stable operation 0 < K < 6
The characteristic equation of a servo system is given by
a0s4 + a1s3 + a2s2 + a3s + a4 = 0
Now, consider the following conditions required to be satisfied by the coefficient of the above characteristic equation for the system to be stable:
1. a1 > 0 and a4 > 0
2. a1 < 0 and a4 > 0
3. a1a2< a0a3
4. a1a2 > a0a3
5. 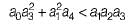
6. 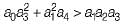
Which of the above conditions holds true for the given system to be stable?- a)2, 3 and 6
- b)1,3 and 5
- c)1,4 and 5
- d)2 and 4
Correct answer is option 'C'. Can you explain this answer?
The characteristic equation of a servo system is given by
a0s4 + a1s3 + a2s2 + a3s + a4 = 0
Now, consider the following conditions required to be satisfied by the coefficient of the above characteristic equation for the system to be stable:
1. a1 > 0 and a4 > 0
2. a1 < 0 and a4 > 0
3. a1a2< a0a3
4. a1a2 > a0a3
5.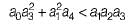
6.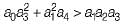
Which of the above conditions holds true for the given system to be stable?
a0s4 + a1s3 + a2s2 + a3s + a4 = 0
Now, consider the following conditions required to be satisfied by the coefficient of the above characteristic equation for the system to be stable:
1. a1 > 0 and a4 > 0
2. a1 < 0 and a4 > 0
3. a1a2< a0a3
4. a1a2 > a0a3
5.
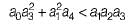
6.
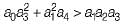
Which of the above conditions holds true for the given system to be stable?
a)
2, 3 and 6
b)
1,3 and 5
c)
1,4 and 5
d)
2 and 4
|
|
Sahil Das answered |
The Rouths array is formed as follows:
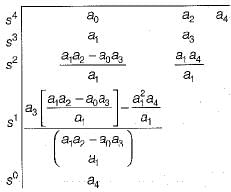
For the system to be stable, there should not be any sign change in the first column of Routh’s array.
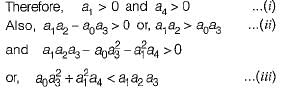
Hence, above conditions must hold for the given system to be stable.

For the system to be stable, there should not be any sign change in the first column of Routh’s array.
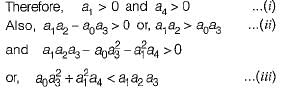
Hence, above conditions must hold for the given system to be stable.
Assertion (A): Location of the poles of a transfer function in the s-plane affects greatly the transient response of the system and hence stability.
Reason (R): The poles that are close to the imaginary axis in the left-half s-plane give rise to transient responses that will decay relatively slowly, whereas the poles that are far away from the axis (relative to the dominant poles) correspond to fast-decaying time responses. - a)Both A and R are true and R is a correct explanation of A,
- b)Both A and R are true but R is not a correct explanation of A.
- c)A is true but R is false.
- d)A is false but R is true.
Correct answer is option 'A'. Can you explain this answer?
Assertion (A): Location of the poles of a transfer function in the s-plane affects greatly the transient response of the system and hence stability.
Reason (R): The poles that are close to the imaginary axis in the left-half s-plane give rise to transient responses that will decay relatively slowly, whereas the poles that are far away from the axis (relative to the dominant poles) correspond to fast-decaying time responses.
Reason (R): The poles that are close to the imaginary axis in the left-half s-plane give rise to transient responses that will decay relatively slowly, whereas the poles that are far away from the axis (relative to the dominant poles) correspond to fast-decaying time responses.
a)
Both A and R are true and R is a correct explanation of A,
b)
Both A and R are true but R is not a correct explanation of A.
c)
A is true but R is false.
d)
A is false but R is true.
|
|
Jiyaan Chopra answered |
Understanding the Assertion and Reason
The assertion (A) and reason (R) provided relate to the impact of pole locations in the s-plane on system behavior, particularly in terms of transient response and stability.
Assertion (A) Explained
- The location of poles in the s-plane is crucial for determining system stability.
- Poles in the left-half plane indicate a stable system; their proximity to the imaginary axis affects how quickly the system responds to inputs.
- A system with poles close to the imaginary axis will exhibit slower decay of transient responses.
Reason (R) Explained
- Poles near the imaginary axis lead to slower-damping responses, resulting in prolonged transient behavior.
- Conversely, poles further from the imaginary axis correspond to rapid decay of transients, allowing the system to settle quickly.
- The dominant poles (the poles closest to the imaginary axis) dictate the transient response, while poles further away have less impact on the overall behavior.
Conclusion
- Both the assertion and reason are correct: A accurately describes the influence of pole locations on stability and transient response, while R provides a valid explanation for why poles near the imaginary axis result in slower responses.
- Therefore, option 'a' is correct: Both A and R are true, and R is a correct explanation of A.
Understanding these concepts is vital for analyzing and designing stable control systems in Electronics and Communication Engineering.
The assertion (A) and reason (R) provided relate to the impact of pole locations in the s-plane on system behavior, particularly in terms of transient response and stability.
Assertion (A) Explained
- The location of poles in the s-plane is crucial for determining system stability.
- Poles in the left-half plane indicate a stable system; their proximity to the imaginary axis affects how quickly the system responds to inputs.
- A system with poles close to the imaginary axis will exhibit slower decay of transient responses.
Reason (R) Explained
- Poles near the imaginary axis lead to slower-damping responses, resulting in prolonged transient behavior.
- Conversely, poles further from the imaginary axis correspond to rapid decay of transients, allowing the system to settle quickly.
- The dominant poles (the poles closest to the imaginary axis) dictate the transient response, while poles further away have less impact on the overall behavior.
Conclusion
- Both the assertion and reason are correct: A accurately describes the influence of pole locations on stability and transient response, while R provides a valid explanation for why poles near the imaginary axis result in slower responses.
- Therefore, option 'a' is correct: Both A and R are true, and R is a correct explanation of A.
Understanding these concepts is vital for analyzing and designing stable control systems in Electronics and Communication Engineering.
The open loop transfer function of a system is as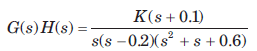 The range of K for stable system will be
The range of K for stable system will be- a)K 0.355
- b)0.149 < K < 0.355
- c)0.236 < K < 0.44
- d)K 0.44
Correct answer is option 'B'. Can you explain this answer?
The open loop transfer function of a system is as
The range of K for stable system will be
a)
K 0.355
b)
0.149 < K < 0.355
c)
0.236 < K < 0.44
d)
K 0.44

|
Nilanjan Rane answered |
The characteristic equation is 1 + G(s)H(s) = 0
⇒ s(s - 0.2)(s2 + s + 0.6)+K(s + 0.1) = 0
s4 +0.8 s3 +0.4s2 +(K - 0.12)s +0.1K = 0
Routh table is as shown in fig. S.62.29
s4 +0.8 s3 +0.4s2 +(K - 0.12)s +0.1K = 0
Routh table is as shown in fig. S.62.29

K > 0, 055 -125K > 0 ⇒ K < 0.44 -125K2 +0.63K -0066 >0
(K - 0.149)(K - 0355) < 0, 0.149 < K < 0.355
The open loop transfer function of a unity feedback system is 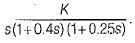
What is the range of value of K so that the closed loop system is absolutely stable?- a)K > 6.5
- b)0 < K < 4.25
- c)0 < K < 9.8
- d)0 < K < 6.5
Correct answer is option 'D'. Can you explain this answer?
The open loop transfer function of a unity feedback system is 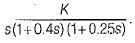
What is the range of value of K so that the closed loop system is absolutely stable?
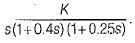
What is the range of value of K so that the closed loop system is absolutely stable?
a)
K > 6.5
b)
0 < K < 4.25
c)
0 < K < 9.8
d)
0 < K < 6.5
|
|
Sanchita Sarkar answered |
The characteristic equation is,
1 + G(s)H(s) = 0

For absolute stability, we have:
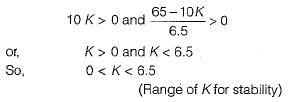
1 + G(s)H(s) = 0

For absolute stability, we have:
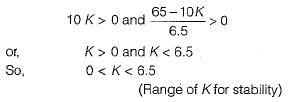
Find the number of poles in the right-half plane (RHP) for the system as shown. Is the system stable?
- a)2 RHP poles; System is unstable
- b)2 RHP poles; System is stable
- c)3 RHP poles; System is unstable
- d)3 RHP poles; System is stable
Correct answer is option 'A'. Can you explain this answer?
Find the number of poles in the right-half plane (RHP) for the system as shown. Is the system stable?

a)
2 RHP poles; System is unstable
b)
2 RHP poles; System is stable
c)
3 RHP poles; System is unstable
d)
3 RHP poles; System is stable

|
Engineers Adda answered |
Concept:
The characteristic equation for a given open-loop transfer function G(s) is
1 + G(s) H(s) = 0
According to the Routh tabulation method,
The system is said to be stable if there are no sign changes in the first column of the Routh array
The number of poles lie on the right half of s plane = number of sign changes
Calculation:
Characteristic equation: 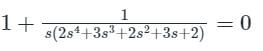
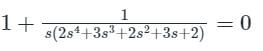
⇒ 2s5 + 3s4 + 2s3 + 3s2 + 2s + 1 = 0
By applying Routh tabulation method,
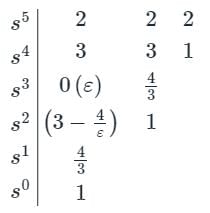
As ε is very small value, (3 – 4/ε) is a negative value and hence there are two sign changes.
Therefore, the number of right-half poles = 2
The system is unstable.
What is the range of K for which the open loop transfer function
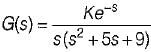
represents an unstable closed loop system?- a)0 < K < 7.5
- b)K < 5
- c)7.5 < K < 0
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
What is the range of K for which the open loop transfer function
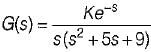
represents an unstable closed loop system?
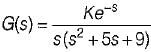
represents an unstable closed loop system?
a)
0 < K < 7.5
b)
K < 5
c)
7.5 < K < 0
d)
None of the above
|
|
Parth Ghoshal answered |
For low frequency, e-s = (1 - s)
∴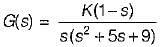
The characteristic equation is
1 + G(s) = 0
or, s(s2 + 5s + 9) + K(1 - s) = 0
or, s3 + 5s2 + ( 9 - K ) s + K = 0
The Routh’s array is

For stability, K > 0 and
∴ 0 < K < 7.5 (for stability)
0 > K > 7.5 (for unstability)
∴
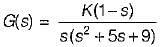
The characteristic equation is
1 + G(s) = 0
or, s(s2 + 5s + 9) + K(1 - s) = 0
or, s3 + 5s2 + ( 9 - K ) s + K = 0
The Routh’s array is

For stability, K > 0 and

∴ 0 < K < 7.5 (for stability)
0 > K > 7.5 (for unstability)
The forward-path transfer function of a ufb system is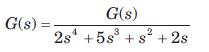 The system is
The system is- a)stable
- b)unstable
- c)marginally stable
- d)more information is required.
Correct answer is option 'B'. Can you explain this answer?
The forward-path transfer function of a ufb system is
The system is
a)
stable
b)
unstable
c)
marginally stable
d)
more information is required.
|
|
Nayanika Deshpande answered |
Closed loop transfer function
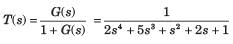
Routh table is as shown in fig. S.6.2.28
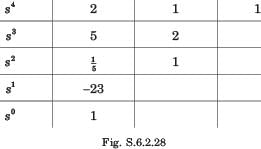
2 RHP poles so unstable.
The closed loop transfer function of a system is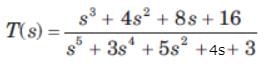 The number of poles in right half-plane and in left half-plane are
The number of poles in right half-plane and in left half-plane are- a)3, 2
- b)2, 3
- c)1, 4
- d)4, 1
Correct answer is option 'B'. Can you explain this answer?
The closed loop transfer function of a system is
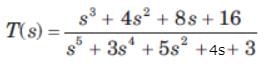
The number of poles in right half-plane and in left half-plane are
a)
3, 2
b)
2, 3
c)
1, 4
d)
4, 1

|
Sagnik Sen answered |
Routh table is as shown in
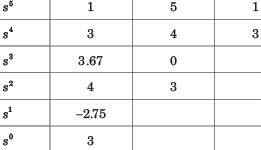
In RHP -2 poles. In LHP -3 poles
The open-loop transfer function of a ufb system is The closed loop system will be stable if the value of K is
The closed loop system will be stable if the value of K is- a)2
- b)3
- c)4
- d)5
Correct answer is option 'D'. Can you explain this answer?
The open-loop transfer function of a ufb system is
The closed loop system will be stable if the value of K is
a)
2
b)
3
c)
4
d)
5
|
|
Arindam Goyal answered |
Routh table is as shown in fig.

200K > 0 → K > 0, 30K2 - 140K > 0
 satisfy this condition.
satisfy this condition.The poles location for this system is shown in fig.The value of K is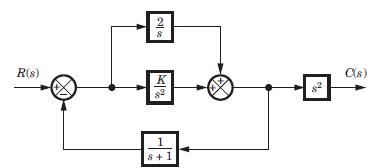
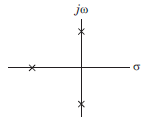
- a)4
- b)-4
- c)2
- d)-2
Correct answer is option 'C'. Can you explain this answer?
The poles location for this system is shown in fig.The value of K is
a)
4
b)
-4
c)
2
d)
-2
|
|
Aarav Kapoor answered |
Denominator = s3 + s2 + 2s + K Routh table is as shown in fig.

Row of zeros when K = 2,
s2 + 2 = 0, ⇒ s = -1, j√2, - j√2
s2 + 2 = 0, ⇒ s = -1, j√2, - j√2
Chapter doubts & questions for Routh-Hurwitz Stability - 6 Months Preparation for GATE Electrical 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Routh-Hurwitz Stability - 6 Months Preparation for GATE Electrical in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
6 Months Preparation for GATE Electrical
675 videos|1297 docs|786 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily