Electrical Engineering (EE) Exam > Electrical Engineering (EE) Questions > Consider the following statements regarding t...
Start Learning for Free
Consider the following statements regarding the characteristic equation of a system given by:
s4 + 5s3 + 25+10 = 0
1. The system is unstable.
2. The system is stable.
3. Number of roots with zero real part - 0
4. Number of roots with positive real part - 4
5. Number of roots with negative real part = 2
Which of the above statements are correct?
s4 + 5s3 + 25+10 = 0
1. The system is unstable.
2. The system is stable.
3. Number of roots with zero real part - 0
4. Number of roots with positive real part - 4
5. Number of roots with negative real part = 2
Which of the above statements are correct?
- a)2 and 3
- b)1 and 3
- c)2, 3 and 4
- d)1, 3 and 5
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider the following statements regarding the characteristic equatio...
The Routh’s array is
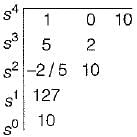
Since there are two sign changes in first column of Routh’s array, therefore the system is unstable.
Number of roots with positive real part = 2
Number of roots with negative real part = 2
Number of roots with zero real part = 0

Since there are two sign changes in first column of Routh’s array, therefore the system is unstable.
Number of roots with positive real part = 2
Number of roots with negative real part = 2
Number of roots with zero real part = 0
Most Upvoted Answer
Consider the following statements regarding the characteristic equatio...
Explanation:
The characteristic equation of a system is obtained by setting the denominator of the transfer function equal to zero. The roots of the characteristic equation are the poles of the transfer function, which determine the stability and behavior of the system.
Characteristics Equation: s4 + 5s3 + 25s2 + 10 = 0
Number of roots with zero real part (i.e., imaginary roots)
The characteristic equation has no pure imaginary roots, so the answer is 0.
Number of roots with positive real part
All the coefficients of the characteristic equation are positive, so there are no positive real roots.
Number of roots with negative real part
The characteristic equation has two pairs of complex conjugate roots, which have negative real parts. So, the answer is 2.
Stability of the system
The system is stable if all the poles lie in the left half of the complex plane, i.e., have negative real parts. Since the characteristic equation has only roots with negative real parts, the system is stable.
Conclusion:
Hence, the correct statements are 2, 3, and 5, i.e., the system is stable, there are no roots with zero real parts, and there are two roots with negative real parts. The statement that the system is unstable (option 1) and the statement that there are four roots with positive real parts (option 4) are incorrect.
The characteristic equation of a system is obtained by setting the denominator of the transfer function equal to zero. The roots of the characteristic equation are the poles of the transfer function, which determine the stability and behavior of the system.
Characteristics Equation: s4 + 5s3 + 25s2 + 10 = 0
Number of roots with zero real part (i.e., imaginary roots)
The characteristic equation has no pure imaginary roots, so the answer is 0.
Number of roots with positive real part
All the coefficients of the characteristic equation are positive, so there are no positive real roots.
Number of roots with negative real part
The characteristic equation has two pairs of complex conjugate roots, which have negative real parts. So, the answer is 2.
Stability of the system
The system is stable if all the poles lie in the left half of the complex plane, i.e., have negative real parts. Since the characteristic equation has only roots with negative real parts, the system is stable.
Conclusion:
Hence, the correct statements are 2, 3, and 5, i.e., the system is stable, there are no roots with zero real parts, and there are two roots with negative real parts. The statement that the system is unstable (option 1) and the statement that there are four roots with positive real parts (option 4) are incorrect.
Free Test
FREE
| Start Free Test |
Community Answer
Consider the following statements regarding the characteristic equatio...
Characteristics of the Given System
The given system can be represented by the characteristic equation s^4 + 5s^3 + 25s^2 + 10 = 0. To analyze the stability of the system, we need to determine the roots of the characteristic equation and examine their real parts.
Finding the Roots of the Characteristic Equation
There are different methods to find the roots of a polynomial equation, such as factoring, synthetic division, or numerical methods. In this case, we can use a numerical solver or the Routh-Hurwitz stability criterion. Applying the latter, we obtain the following Routh array:
s^4 1 25
s^3 5 10
s^2 5/7 0
s^1 10/7 0
s^0 10/7 0
The first column of the array corresponds to the coefficients of the s^n terms in the characteristic equation. The subsequent columns are obtained by computing the coefficients of the s^(n-1) terms using the previous row of the array. The entries in each row alternate in sign and must be nonzero to ensure that the roots have negative real parts (i.e., stable). The number of sign changes in the first column gives the maximum number of roots with positive real parts (i.e., unstable).
In this case, the first column has two sign changes, implying that there are two roots with positive real parts. Therefore, statement 4 is incorrect.
The second column has a zero entry, which means there is one root with zero real part, as stated in statement 3.
The entries in the third column are positive, indicating that all the roots have negative real parts. However, the last row has a zero entry, which implies that the system is marginally stable. Therefore, statement 2 is correct but incomplete.
The first column has a positive leading coefficient, indicating that the system is unstable. Therefore, statement 1 is correct.
Conclusion
In summary, statements 1, 3, and 5 are correct, while statements 2 and 4 are incorrect. The given system is marginally stable, with no roots in the right-half plane but one root with zero real part.
The given system can be represented by the characteristic equation s^4 + 5s^3 + 25s^2 + 10 = 0. To analyze the stability of the system, we need to determine the roots of the characteristic equation and examine their real parts.
Finding the Roots of the Characteristic Equation
There are different methods to find the roots of a polynomial equation, such as factoring, synthetic division, or numerical methods. In this case, we can use a numerical solver or the Routh-Hurwitz stability criterion. Applying the latter, we obtain the following Routh array:
s^4 1 25
s^3 5 10
s^2 5/7 0
s^1 10/7 0
s^0 10/7 0
The first column of the array corresponds to the coefficients of the s^n terms in the characteristic equation. The subsequent columns are obtained by computing the coefficients of the s^(n-1) terms using the previous row of the array. The entries in each row alternate in sign and must be nonzero to ensure that the roots have negative real parts (i.e., stable). The number of sign changes in the first column gives the maximum number of roots with positive real parts (i.e., unstable).
In this case, the first column has two sign changes, implying that there are two roots with positive real parts. Therefore, statement 4 is incorrect.
The second column has a zero entry, which means there is one root with zero real part, as stated in statement 3.
The entries in the third column are positive, indicating that all the roots have negative real parts. However, the last row has a zero entry, which implies that the system is marginally stable. Therefore, statement 2 is correct but incomplete.
The first column has a positive leading coefficient, indicating that the system is unstable. Therefore, statement 1 is correct.
Conclusion
In summary, statements 1, 3, and 5 are correct, while statements 2 and 4 are incorrect. The given system is marginally stable, with no roots in the right-half plane but one root with zero real part.
Attention Electrical Engineering (EE) Students!
To make sure you are not studying endlessly, EduRev has designed Electrical Engineering (EE) study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in Electrical Engineering (EE).

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Similar Electrical Engineering (EE) Doubts
Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer?
Question Description
Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer? for Electrical Engineering (EE) 2024 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer?.
Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer? for Electrical Engineering (EE) 2024 is part of Electrical Engineering (EE) preparation. The Question and answers have been prepared according to the Electrical Engineering (EE) exam syllabus. Information about Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for Electrical Engineering (EE) 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer?.
Solutions for Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for Electrical Engineering (EE).
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Here you can find the meaning of Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer?, a detailed solution for Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider the following statements regarding the characteristic equation of a system given by:s4 + 5s3 + 25+10 = 01. The system is unstable.2. The system is stable.3. Number of roots with zero real part - 04. Number of roots with positive real part - 45. Number of roots with negative real part = 2Which of the above statements are correct?a)2 and 3 b)1 and 3c)2, 3 and 4 d)1, 3 and 5Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice Electrical Engineering (EE) tests.

|
Explore Courses for Electrical Engineering (EE) exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























