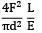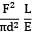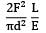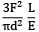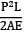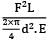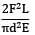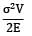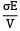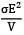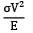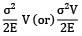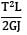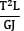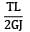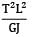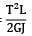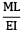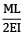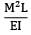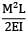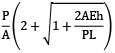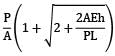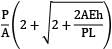All Exams >
Mechanical Engineering >
6 Months Preparation for GATE Mechanical >
All Questions
All questions of Strain Energy for Mechanical Engineering Exam
Strain energy stored in a solid circular shaft subjected to torsion is proportional to- a) GJ
- b) (GJ)2
- c) 1/GJ
- d) 1/(GJ)2
Correct answer is option 'C'. Can you explain this answer?
Strain energy stored in a solid circular shaft subjected to torsion is proportional to
a)
GJ
b)
(GJ)2
c)
1/GJ
d)
1/(GJ)2

|
Pioneer Academy answered |
Strain energy due to torsion
U = 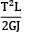
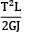
∴ U ∝ 1/GJ
Which one of the following statements is correct? The work done in stretching an elastic string varies- a) as the square of the extension
- b) as the square root of the extension
- c) linearly with the extension
- d) as the cube root of the extension
Correct answer is option 'A'. Can you explain this answer?
Which one of the following statements is correct? The work done in stretching an elastic string varies
a)
as the square of the extension
b)
as the square root of the extension
c)
linearly with the extension
d)
as the cube root of the extension

|
Telecom Tuners answered |
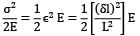
A bar having length L and uniform cross section with area A is subjected to both tensile force P and torque T. If G is the shear modulus and E is the Young’s modulus, the internal strain energy stored in the bar is- a)
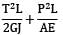
- b)

- c)
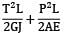
- d)
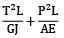
Correct answer is option 'C'. Can you explain this answer?
A bar having length L and uniform cross section with area A is subjected to both tensile force P and torque T. If G is the shear modulus and E is the Young’s modulus, the internal strain energy stored in the bar is
a)
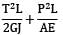
b)

c)
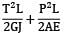
d)
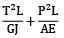

|
Musa Tunkara Tunkara answered |
C
Modulus of resilience is defined as- a) proof resilience of a material per unit length
- b) proof resilience of a material per unit area
- c) proof resilience of a material per unit volume
- d) proof resilience of a material per unit energy
Correct answer is option 'C'. Can you explain this answer?
Modulus of resilience is defined as
a)
proof resilience of a material per unit length
b)
proof resilience of a material per unit area
c)
proof resilience of a material per unit volume
d)
proof resilience of a material per unit energy
|
|
Sanvi Kapoor answered |
Modulus of resilience is the proof resilience per unit volume.
If σ and E for a body of volume 2 × 105 mm3 are 10 N/mm2 and 1 × 105 N/mm2, Resilience of the body is- a) 100 N-mm
- b) 120 N-mm
- c) 125 kNm
- d) 312.5 kNm
Correct answer is option 'A'. Can you explain this answer?
If σ and E for a body of volume 2 × 105 mm3 are 10 N/mm2 and 1 × 105 N/mm2, Resilience of the body is
a)
100 N-mm
b)
120 N-mm
c)
125 kNm
d)
312.5 kNm
|
|
Sanvi Kapoor answered |
Σ = 10N/mm2
E = 1 × 105N/mm2
V = 2 × 105N/mm3
U = 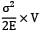
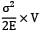
U = 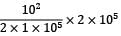
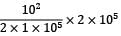
= 100 Nmm
The strain energy stored in a body due to suddenly applied load compared to when it is applied gradually is
- a)same
- b)four times
- c)twice times
- d)one times
Correct answer is option 'B'. Can you explain this answer?
The strain energy stored in a body due to suddenly applied load compared to when it is applied gradually is
a)
same
b)
four times
c)
twice times
d)
one times
|
|
Sanvi Kapoor answered |
σ gradual = σ, σsudden = 2σ. The strain energy stored in a body due to suddenly applied load compared to when it is applied gradually is four times.
The maximum stress produced in a bar when a load is applied suddenly is 40N/mm2. If the same load is applied gradually, the stress produced is- a) 10 N/mm2
- b) 20 N/mm2
- c) 40 N/mm2
- d) 80 N/mm2
Correct answer is option 'B'. Can you explain this answer?
The maximum stress produced in a bar when a load is applied suddenly is 40N/mm2. If the same load is applied gradually, the stress produced is
a)
10 N/mm2
b)
20 N/mm2
c)
40 N/mm2
d)
80 N/mm2
|
|
Zoya Sharma answered |
Σsudden = 2σgradual
40 = 2(σgradual)
σgradual = 20N/mm2
The strain energy in bar of 20 mm diameter, 1.0 m length, and young’s modulus 200.0 GPa under an axial force of 100.0 N is- a) 0.0796 N-mm
- b) 0.796 kNm
- c) 0.080 Nm
- d) 0.080 kNm
Correct answer is option 'A'. Can you explain this answer?
The strain energy in bar of 20 mm diameter, 1.0 m length, and young’s modulus 200.0 GPa under an axial force of 100.0 N is
a)
0.0796 N-mm
b)
0.796 kNm
c)
0.080 Nm
d)
0.080 kNm
|
|
Pritam Jain answered |
Calculation of Strain Energy in Bar
Given parameters are:
- Diameter (d) = 20 mm
- Length (L) = 1.0 m
- Young's Modulus (E) = 200.0 GPa
- Axial Force (F) = 100.0 N
Formula for Strain Energy:
Strain Energy (U) = (1/2) x (F/A) x δ
where,
- F = Axial Force
- A = Cross-sectional Area of Bar
- δ = Elongation or Deformation in Bar
Calculation of Cross-sectional Area:
Cross-sectional Area (A) = π/4 x d²
= 3.14/4 x (20 mm)²
= 314.16 mm²
Calculation of Elongation or Deformation:
Elongation or Deformation (δ) = F x L / A x E
= 100.0 N x 1.0 m / 314.16 mm² x 200.0 GPa
= 0.000159
Calculation of Strain Energy:
Strain Energy (U) = (1/2) x (F/A) x δ
= (1/2) x (100.0 N / 314.16 mm²) x 0.000159
= 0.0796 N-mm
Therefore, the strain energy in the bar is 0.0796 N-mm (Option A).
Given parameters are:
- Diameter (d) = 20 mm
- Length (L) = 1.0 m
- Young's Modulus (E) = 200.0 GPa
- Axial Force (F) = 100.0 N
Formula for Strain Energy:
Strain Energy (U) = (1/2) x (F/A) x δ
where,
- F = Axial Force
- A = Cross-sectional Area of Bar
- δ = Elongation or Deformation in Bar
Calculation of Cross-sectional Area:
Cross-sectional Area (A) = π/4 x d²
= 3.14/4 x (20 mm)²
= 314.16 mm²
Calculation of Elongation or Deformation:
Elongation or Deformation (δ) = F x L / A x E
= 100.0 N x 1.0 m / 314.16 mm² x 200.0 GPa
= 0.000159
Calculation of Strain Energy:
Strain Energy (U) = (1/2) x (F/A) x δ
= (1/2) x (100.0 N / 314.16 mm²) x 0.000159
= 0.0796 N-mm
Therefore, the strain energy in the bar is 0.0796 N-mm (Option A).
An axial load of 100kN is applied onto a bar of length 3 m and cross-sectional area of 100 mm2. If E = 200 kN/mm2 the total strain energy in the bar is equal to- a) 750 N-mm
- b) 7500 N-mm
- c) 75,000 N-mm
- d) 7,50,000 N-mm
Correct answer is option 'D'. Can you explain this answer?
An axial load of 100kN is applied onto a bar of length 3 m and cross-sectional area of 100 mm2. If E = 200 kN/mm2 the total strain energy in the bar is equal to
a)
750 N-mm
b)
7500 N-mm
c)
75,000 N-mm
d)
7,50,000 N-mm
|
|
Lavanya Menon answered |
Axial load, P = 100 × 103N
Length, L = 3000 mm 2
Cross section area, A = 100 mm E = 200 × 103 N/mm2
U =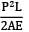
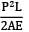
= 

= 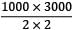
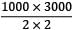
= 750000 Nmm
Modulus of resilience of a material is the area of the stress-strain curve up to- a) failure
- b) upper yield point (
- c)proportionality limit
- d) elastic limit
Correct answer is option 'D'. Can you explain this answer?
Modulus of resilience of a material is the area of the stress-strain curve up to
a)
failure
b)
upper yield point (
c)
proportionality limit
d)
elastic limit

|
Cstoppers Instructors answered |
Modulus of resilience is the area under the stress strain curve up to the elastic limit.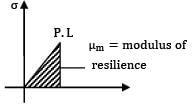

A load P is applied onto a body gradually and the elongation observed is 12 mm. If the same load P is applied suddenly. The instantaneous elongation in the body will be- a) 12 mm
- b) 24 mm
- c) 6 mm
- d) 3 mm
Correct answer is option 'B'. Can you explain this answer?
A load P is applied onto a body gradually and the elongation observed is 12 mm. If the same load P is applied suddenly. The instantaneous elongation in the body will be
a)
12 mm
b)
24 mm
c)
6 mm
d)
3 mm
|
|
Avik Ghosh answered |
Understanding Elongation under Load
When a load P is applied to a material, the nature of the loading (gradual vs. sudden) significantly affects the elongation experienced by the material.
Gradual Load Application
- When the load is applied gradually, the material has time to deform elastically without much internal stress concentration.
- In this scenario, the elongation observed is 12 mm.
Sudden Load Application
- Applying the same load suddenly means that the load is applied in an instant, which causes different behavior in the material.
- The sudden application leads to higher stress and strain rates, as the material does not have time to adjust to the load.
Impact on Elongation
- The sudden application generally results in a larger elongation due to dynamic effects.
- Typically, the elongation can increase by a factor due to inertia and impact, often approximated to be double the elongation from gradual loading.
Conclusion
- Since the elongation observed under gradual loading is 12 mm, under sudden loading, the material experiences approximately double the elongation.
- Therefore, the instantaneous elongation with load P applied suddenly will be 24 mm.
This reasoning leads to the conclusion that the correct answer is option 'B', which states that the instantaneous elongation will be 24 mm.
When a load P is applied to a material, the nature of the loading (gradual vs. sudden) significantly affects the elongation experienced by the material.
Gradual Load Application
- When the load is applied gradually, the material has time to deform elastically without much internal stress concentration.
- In this scenario, the elongation observed is 12 mm.
Sudden Load Application
- Applying the same load suddenly means that the load is applied in an instant, which causes different behavior in the material.
- The sudden application leads to higher stress and strain rates, as the material does not have time to adjust to the load.
Impact on Elongation
- The sudden application generally results in a larger elongation due to dynamic effects.
- Typically, the elongation can increase by a factor due to inertia and impact, often approximated to be double the elongation from gradual loading.
Conclusion
- Since the elongation observed under gradual loading is 12 mm, under sudden loading, the material experiences approximately double the elongation.
- Therefore, the instantaneous elongation with load P applied suddenly will be 24 mm.
This reasoning leads to the conclusion that the correct answer is option 'B', which states that the instantaneous elongation will be 24 mm.
Consider the following statements.(P) Hardness is the resistance of a material to indentation.(Q) Elastic modulus is a measure of ductility.(R) Deflection depends on stiffness.(S) The total area under the stress-strain curve is a measure of resilience.Among the above statements, the correct ones are- a) P and Q only
- b) Q and S only
- c) P and R only
- d) R and S only
Correct answer is option 'C'. Can you explain this answer?
Consider the following statements.
(P) Hardness is the resistance of a material to indentation.
(Q) Elastic modulus is a measure of ductility.
(R) Deflection depends on stiffness.
(S) The total area under the stress-strain curve is a measure of resilience.
Among the above statements, the correct ones are
a)
P and Q only
b)
Q and S only
c)
P and R only
d)
R and S only
|
|
Zoya Sharma answered |
Percentage elongation is a measure of ductility. The total area under the stress-strain curve is a measure of modulus of toughness.
The maximum strain energy stored in a body without permanent deformation is- a) resilience
- b) proof resilience
- c) modulus of resilience
- d) impact resilience
Correct answer is option 'B'. Can you explain this answer?
The maximum strain energy stored in a body without permanent deformation is
a)
resilience
b)
proof resilience
c)
modulus of resilience
d)
impact resilience
|
|
Rajat Khanna answered |
**Proof Resilience**
The maximum strain energy stored in a body without permanent deformation is known as proof resilience. It is a measure of the ability of a material to absorb energy up to the elastic limit without undergoing permanent deformation. Proof resilience is an important property of materials used in engineering applications as it determines their ability to withstand impact or sudden loads without deforming or breaking.
**Explanation:**
When a load is applied to a material, it deforms elastically up to a certain point. This elastic deformation is reversible, meaning that the material can return to its original shape once the load is removed. The energy stored in the material during this elastic deformation is known as strain energy.
However, if the load exceeds a certain threshold, the material will undergo plastic deformation, which is irreversible and leads to permanent deformation. The energy required to cause this permanent deformation is known as the yield strength of the material.
The proof resilience is defined as the maximum strain energy that a material can absorb up to the yield point without permanent deformation. It is calculated as the area under the stress-strain curve up to the yield point.
By definition, the proof resilience is a measure of the material's ability to absorb energy without permanent deformation. It represents the maximum amount of energy that can be stored in the material and released when the load is removed without causing any permanent changes in the material's structure.
In practical terms, materials with high proof resilience are desirable in applications where they are subjected to impact or sudden loads. For example, in the construction of bridges, buildings, or automotive components, materials with high proof resilience are preferred as they can withstand sudden loads or impacts without permanent deformation or failure.
In conclusion, the maximum strain energy stored in a body without permanent deformation is known as proof resilience. It represents the ability of a material to absorb energy up to the elastic limit without undergoing permanent deformation.
The maximum strain energy stored in a body without permanent deformation is known as proof resilience. It is a measure of the ability of a material to absorb energy up to the elastic limit without undergoing permanent deformation. Proof resilience is an important property of materials used in engineering applications as it determines their ability to withstand impact or sudden loads without deforming or breaking.
**Explanation:**
When a load is applied to a material, it deforms elastically up to a certain point. This elastic deformation is reversible, meaning that the material can return to its original shape once the load is removed. The energy stored in the material during this elastic deformation is known as strain energy.
However, if the load exceeds a certain threshold, the material will undergo plastic deformation, which is irreversible and leads to permanent deformation. The energy required to cause this permanent deformation is known as the yield strength of the material.
The proof resilience is defined as the maximum strain energy that a material can absorb up to the yield point without permanent deformation. It is calculated as the area under the stress-strain curve up to the yield point.
By definition, the proof resilience is a measure of the material's ability to absorb energy without permanent deformation. It represents the maximum amount of energy that can be stored in the material and released when the load is removed without causing any permanent changes in the material's structure.
In practical terms, materials with high proof resilience are desirable in applications where they are subjected to impact or sudden loads. For example, in the construction of bridges, buildings, or automotive components, materials with high proof resilience are preferred as they can withstand sudden loads or impacts without permanent deformation or failure.
In conclusion, the maximum strain energy stored in a body without permanent deformation is known as proof resilience. It represents the ability of a material to absorb energy up to the elastic limit without undergoing permanent deformation.
Strain energy is used to find- a) stiffness
- b) moment of inertia
- c) deflection
- d) None of these
Correct answer is option 'C'. Can you explain this answer?
Strain energy is used to find
a)
stiffness
b)
moment of inertia
c)
deflection
d)
None of these

|
Asha Nambiar answered |
Strain energy is a concept used in the field of mechanical engineering to analyze and understand the behavior of materials under applied loads. It is a form of potential energy that is stored within a material when it is deformed or strained.
The correct answer to the given question is option 'C', which states that strain energy is used to find deflection. This is because strain energy is directly related to the amount of deformation or deflection that a material undergoes when subjected to an external force.
Here is a detailed explanation of why strain energy is used to find deflection:
1. Strain Energy:
Strain energy is the energy stored within a material when it is subjected to external forces. It is a result of the elastic deformation of the material. When a material is loaded, it deforms and stores energy in the form of potential energy within its structure. This energy is referred to as strain energy.
2. Relationship between Strain Energy and Deflection:
The amount of strain energy stored in a material is directly related to the amount of deformation or deflection that the material undergoes. As the material deforms, its molecules are displaced from their original positions, causing a change in the internal potential energy. This change in potential energy is quantified as strain energy.
3. Deflection Calculation:
Deflection refers to the displacement or bending that a material undergoes when subjected to an external load. It is an important parameter to consider in structural analysis and design. By calculating the strain energy stored in a material, the deflection can be determined.
4. Strain Energy Method:
The strain energy method is a commonly used approach to calculate deflection in engineering structures. It involves determining the potential energy stored within a material due to deformation and equating it to the work done by the external loads. By solving this equation, the deflection of the structure can be determined.
Conclusion:
In conclusion, strain energy is used to find deflection in mechanical engineering. It is a measure of the potential energy stored within a material due to deformation. By calculating the strain energy, the amount of deflection that a material undergoes can be determined. This information is crucial in the analysis and design of engineering structures.
The correct answer to the given question is option 'C', which states that strain energy is used to find deflection. This is because strain energy is directly related to the amount of deformation or deflection that a material undergoes when subjected to an external force.
Here is a detailed explanation of why strain energy is used to find deflection:
1. Strain Energy:
Strain energy is the energy stored within a material when it is subjected to external forces. It is a result of the elastic deformation of the material. When a material is loaded, it deforms and stores energy in the form of potential energy within its structure. This energy is referred to as strain energy.
2. Relationship between Strain Energy and Deflection:
The amount of strain energy stored in a material is directly related to the amount of deformation or deflection that the material undergoes. As the material deforms, its molecules are displaced from their original positions, causing a change in the internal potential energy. This change in potential energy is quantified as strain energy.
3. Deflection Calculation:
Deflection refers to the displacement or bending that a material undergoes when subjected to an external load. It is an important parameter to consider in structural analysis and design. By calculating the strain energy stored in a material, the deflection can be determined.
4. Strain Energy Method:
The strain energy method is a commonly used approach to calculate deflection in engineering structures. It involves determining the potential energy stored within a material due to deformation and equating it to the work done by the external loads. By solving this equation, the deflection of the structure can be determined.
Conclusion:
In conclusion, strain energy is used to find deflection in mechanical engineering. It is a measure of the potential energy stored within a material due to deformation. By calculating the strain energy, the amount of deflection that a material undergoes can be determined. This information is crucial in the analysis and design of engineering structures.
The maximum strain energy stored in a material at its elastic limit per unit volume is known as- a) resilience
- b) proof resilience
- c) modulus of resilience
- d) toughness modulus
Correct answer is option 'C'. Can you explain this answer?
The maximum strain energy stored in a material at its elastic limit per unit volume is known as
a)
resilience
b)
proof resilience
c)
modulus of resilience
d)
toughness modulus
|
|
Sanskriti Chakraborty answered |
**Explanation:**
The maximum strain energy stored in a material at its elastic limit per unit volume is known as the modulus of resilience. Let's understand the concept in detail:
**Resilience:**
- Resilience is a measure of a material's ability to absorb energy when deformed elastically and then release that energy upon unloading.
- It represents the amount of strain energy stored in a material up to its elastic limit.
- Resilience is given by the area under the stress-strain curve up to the elastic limit.
- Resilience is expressed in terms of stress and strain.
**Proof Resilience:**
- Proof resilience is the maximum energy that can be absorbed by a material without permanent deformation.
- It is the area under the stress-strain curve up to the elastic limit.
- Proof resilience is expressed in terms of stress and strain.
**Modulus of Resilience:**
- The modulus of resilience is the maximum strain energy stored in a material at its elastic limit per unit volume.
- It is a measure of a material's ability to absorb and store energy elastically.
- The modulus of resilience is calculated by taking the integral of the stress-strain curve up to the elastic limit.
- It is expressed in terms of stress and strain.
**Toughness Modulus:**
- Toughness is a measure of a material's ability to absorb energy up to fracture.
- It represents the total area under the stress-strain curve.
- Toughness is given by the integral of the stress-strain curve up to fracture.
- Toughness is expressed in terms of stress and strain.
**Conclusion:**
The modulus of resilience is the correct answer because it specifically refers to the maximum strain energy stored in a material at its elastic limit per unit volume. Resilience, proof resilience, and toughness modulus are related concepts but do not specifically represent this particular measure of strain energy.
The maximum strain energy stored in a material at its elastic limit per unit volume is known as the modulus of resilience. Let's understand the concept in detail:
**Resilience:**
- Resilience is a measure of a material's ability to absorb energy when deformed elastically and then release that energy upon unloading.
- It represents the amount of strain energy stored in a material up to its elastic limit.
- Resilience is given by the area under the stress-strain curve up to the elastic limit.
- Resilience is expressed in terms of stress and strain.
**Proof Resilience:**
- Proof resilience is the maximum energy that can be absorbed by a material without permanent deformation.
- It is the area under the stress-strain curve up to the elastic limit.
- Proof resilience is expressed in terms of stress and strain.
**Modulus of Resilience:**
- The modulus of resilience is the maximum strain energy stored in a material at its elastic limit per unit volume.
- It is a measure of a material's ability to absorb and store energy elastically.
- The modulus of resilience is calculated by taking the integral of the stress-strain curve up to the elastic limit.
- It is expressed in terms of stress and strain.
**Toughness Modulus:**
- Toughness is a measure of a material's ability to absorb energy up to fracture.
- It represents the total area under the stress-strain curve.
- Toughness is given by the integral of the stress-strain curve up to fracture.
- Toughness is expressed in terms of stress and strain.
**Conclusion:**
The modulus of resilience is the correct answer because it specifically refers to the maximum strain energy stored in a material at its elastic limit per unit volume. Resilience, proof resilience, and toughness modulus are related concepts but do not specifically represent this particular measure of strain energy.
Chapter doubts & questions for Strain Energy - 6 Months Preparation for GATE Mechanical 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Strain Energy - 6 Months Preparation for GATE Mechanical in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
6 Months Preparation for GATE Mechanical
499 videos|1037 docs|710 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily