All Exams >
Mechanical Engineering >
6 Months Preparation for GATE Mechanical >
All Questions
All questions of Fluid Pressure & Its Measurement for Mechanical Engineering Exam
In Figure below, both fluids are at 20°C. If surface tension effects are negligible, what is the density of the oil, in kg/m3?
- a)788
- b)778
- c)748
- d)758
Correct answer is option 'C'. Can you explain this answer?
In Figure below, both fluids are at 20°C. If surface tension effects are negligible, what is the density of the oil, in kg/m3?

a)
788
b)
778
c)
748
d)
758

|
Gate Funda answered |
Explanation: Move around the U-tube from left atmosphere to right atmosphere:
Pa= (9790N/m3)(0.06m) - γoil(0.08m)= Pa
solve for γoil≈ 7343N/m3,
or: ρoil= 7343/9,81≈ 748kg/m3
Gate AB in figure is 1.2 m wide (in a direction perpendicular to the plane of the figure) and is hinged at A. Gauge G reads −0.147 bar and oil in the right hand tank is having a relative density 0.75. What horizontal force must be applied at B for equilibrium of gate AB?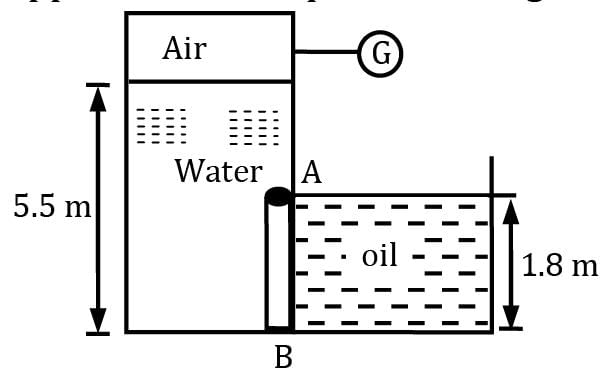 Correct answer is 'Range: 26 to 27'. Can you explain this answer?
Correct answer is 'Range: 26 to 27'. Can you explain this answer?
Gate AB in figure is 1.2 m wide (in a direction perpendicular to the plane of the figure) and is hinged at A. Gauge G reads −0.147 bar and oil in the right hand tank is having a relative density 0.75. What horizontal force must be applied at B for equilibrium of gate AB?


|
Vertex Academy answered |
Force on gate due to water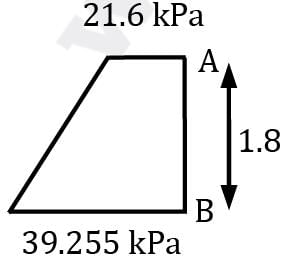
= ρghC(Area) + (pair Gauge)(Area)
= Area (103 × g × (3.7 + 0.9) − 0.147 × 105)
= 65.72 kN
Force on gate due to oil
= ρoil × g × hC × Area
= 0.75 × 103 × 9.81 × 1.8 / 2 × 1.2 × 1.8
= 14.30 kN
The center of pressure for water force can be calculated using pressure triangle

yP = h / 3×(2 × 21.6 + 39.25) / (21.6 + 39.25)
= 0.81 m from bottom
Similarly centre of pressure on oil side
= 0.6 m from the bottom i. e
For equilibrium about A Fw × (1.8 − 0.81)
= Foil (1.8 − 0.6) + FH (1.8)
⇒ 65.72 × 0.99
= 14.3(1.2) + FH × 1.8
FH = 26.61 kN
A 3-m-high, 6-m-wide rectangular gate is hinged at the top edge at A and is restrained by a fixed ridge at B. Determine the hydrostatic force exerted on the gate by the 5-m-high water and the location of the pressure center.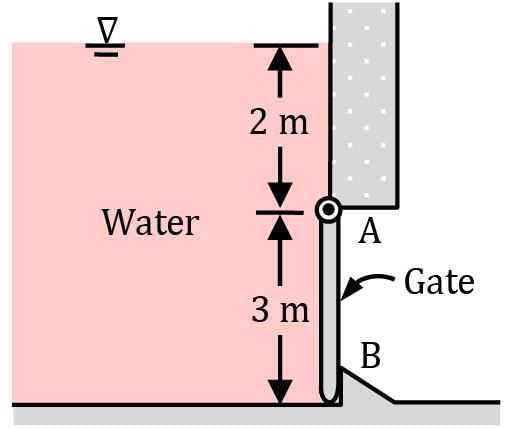 Correct answer is 'Range: 3.7 to 3.72'. Can you explain this answer?
Correct answer is 'Range: 3.7 to 3.72'. Can you explain this answer?
A 3-m-high, 6-m-wide rectangular gate is hinged at the top edge at A and is restrained by a fixed ridge at B. Determine the hydrostatic force exerted on the gate by the 5-m-high water and the location of the pressure center.


|
Engineers Adda answered |
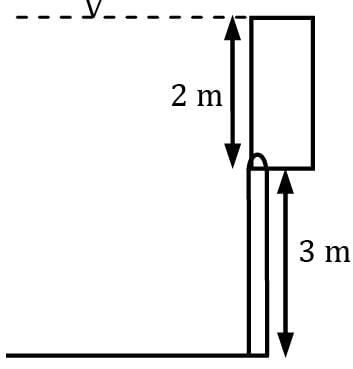
The total force on gate = ρg hc × !rea = 103 × g × (2 + 1.5) × (3 × 6) = 618.03 kN The center of Pressure will be at the center of the pressure diagram
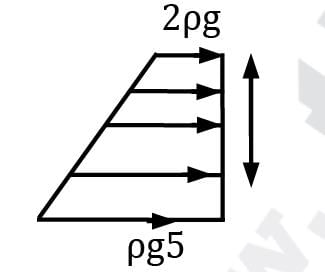
1 / 3× (2 × 5ρg + 2ρg) / 7ρg × 3 = 12 / 7 = 1.714 m
So the center of pressure is (2 + 1.714)
= 3.714 m from the free surface
The 200-kg, 5-m-wide rectangular gate shown in figure is hinged at B and leans against the floor at A making an angle of 45° with the horizontal. The gate is to be opened from its lower edge by applying a normal force at its center. Determine the minimum force F required to open the water gate.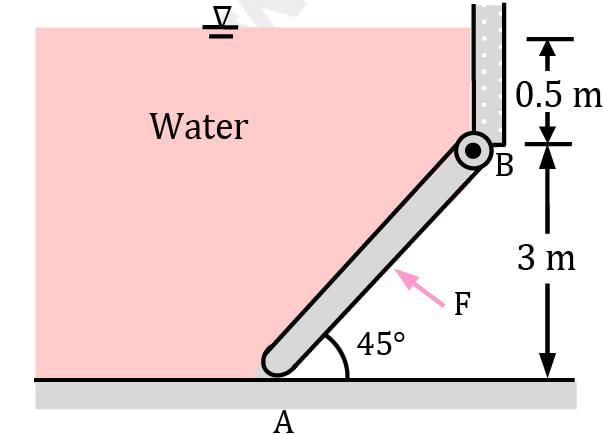
- a) 420
- b) 520
- c) 620
- d) 720
Correct answer is option 'B'. Can you explain this answer?
The 200-kg, 5-m-wide rectangular gate shown in figure is hinged at B and leans against the floor at A making an angle of 45° with the horizontal. The gate is to be opened from its lower edge by applying a normal force at its center. Determine the minimum force F required to open the water gate.

a)
420
b)
520
c)
620
d)
720

|
Engineers Adda answered |
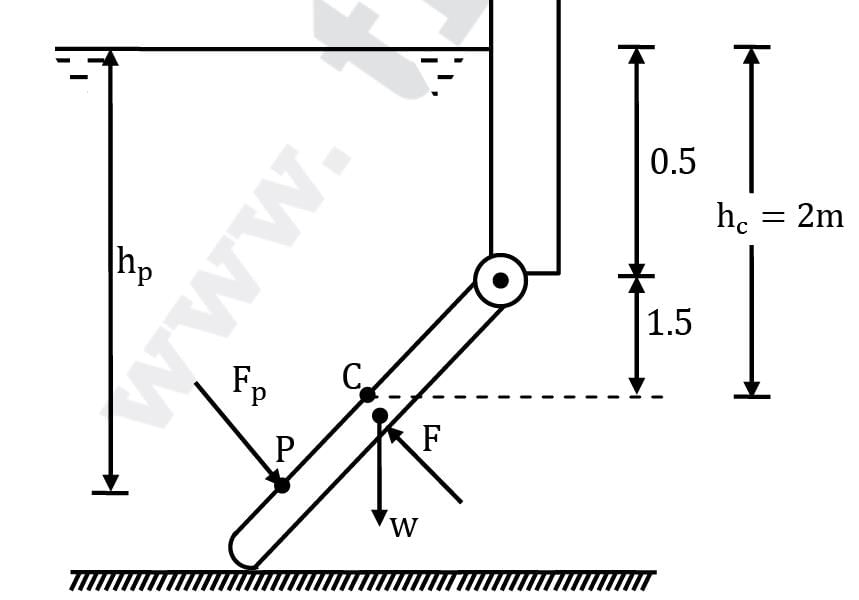
For the surface the gate
hc = 2 m
∴ hp = hc + IG / Ahc sin2θ
hp = 2 + 5×(3√2) 3 / 12 / 5 × 3√2 × 2 × 1 / 2
hp = 2 + 9 × 2 / 12 × 2×1 / 2
hp = 2.375 m
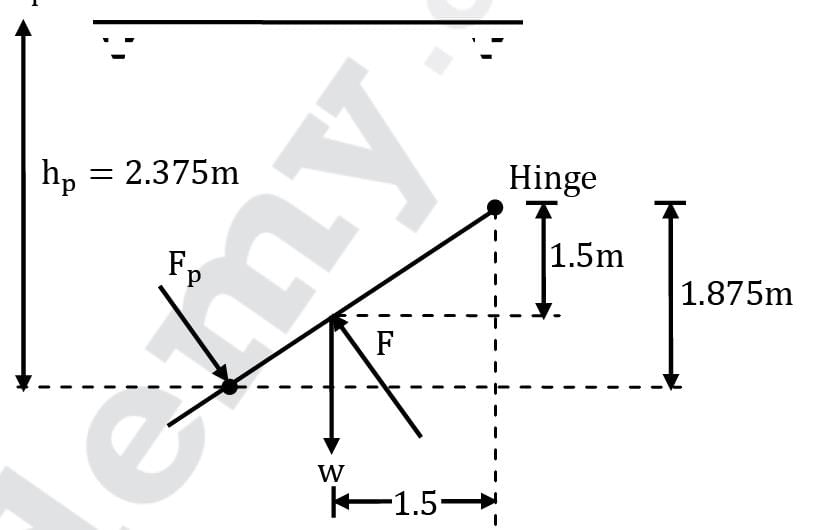
Also Fp = ρgAhc
Fp = 1000 × 9.81 × (5 × 3√2) × 2
Fp = 416.2 kN
Fp × 1.875√2 + w × 1.5 = F × 1.5√2
F = 521 kN
A hydraulic press has a ram of 30 cm diameter and a plunger of 4.5 cm diameter. What is the weight lifted by the hydraulic press when the force applied at the plunger is 600 N?- a)25.67 kN
- b)26.67 kN
- c)28.67 kN
- d)24.67 kN
Correct answer is option 'B'. Can you explain this answer?
A hydraulic press has a ram of 30 cm diameter and a plunger of 4.5 cm diameter. What is the weight lifted by the hydraulic press when the force applied at the plunger is 600 N?
a)
25.67 kN
b)
26.67 kN
c)
28.67 kN
d)
24.67 kN

|
Sreemoyee Chauhan answered |

Which tumbler weighs more?- a) A
- b) B
- c) Both weight same
- d) Cannot be predicted
Correct answer is option 'C'. Can you explain this answer?
Which tumbler weighs more?
a)
A
b)
B
c)
Both weight same
d)
Cannot be predicted
|
|
Sanya Agarwal answered |
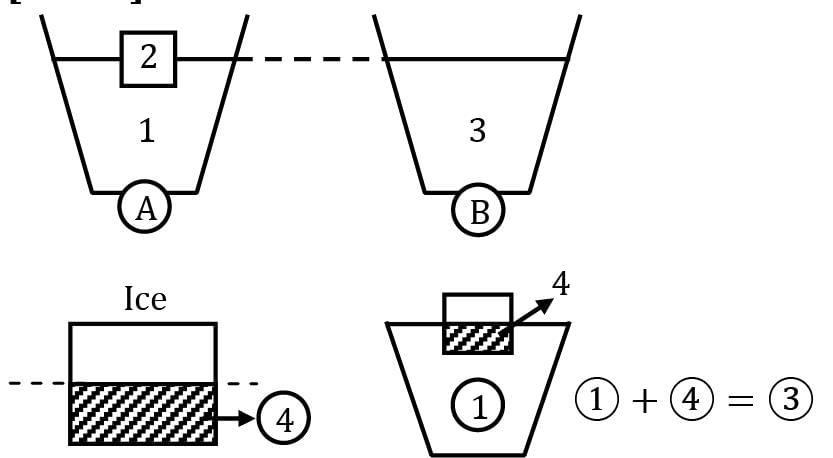
WA = W1 + W2
WA = ρwV1g + ρiV2g WB = ρwVbg
Consider A, as ice is floating, weight of ice is equal to weight of water displaced. ρiV2g = ρwV4g ∴ WA = ρwV1g + ρwV4g
WA = ρw(V1 + V4)g
WA = ρwV3g
WA = WB
Hence the two tumblers weigh the same.
A manometer is used to measure the pressure of a gas in a tank. The fluid used has a specific gravity of 0.85 and the manometer column height is 55 cm, as shown in figure. If the local atmospheric pressure is 96 kPa, what is the absolute pressure in the tank?
- a) 4.6 kPa
- b) 98.6 kPa
- c) 100.6 kPa
- d) 200 kPa
Correct answer is option 'C'. Can you explain this answer?
A manometer is used to measure the pressure of a gas in a tank. The fluid used has a specific gravity of 0.85 and the manometer column height is 55 cm, as shown in figure. If the local atmospheric pressure is 96 kPa, what is the absolute pressure in the tank?

a)
4.6 kPa
b)
98.6 kPa
c)
100.6 kPa
d)
200 kPa

|
Gate Gurus answered |

By equating pressure at A-A’ in the two arms of manometer p = patm + ρgh − ρgas gx Note: as the density of gas is not given. The term ρgas × g x (where x: height of gas column and ρgas is density of gas) can be neglected.
p = 96 × 103 + 850 × 9.81 × 0.55
p = 100.58 kPa
∴ p ≃ 100.6 kPa
A 1-m-diameter, 2-m-high vertical cylinder is completely filled with gasoline whose density is 740 kg/m3. The tank is now rotated about its vertical axis at a rate of 90 rpm, while being accelerated upward at 5 m/s2. Determine(i) the difference between the pressure at the centers of the bottom and top surfaces(ii) the difference between the pressures at the center and the edge of the bottom surface.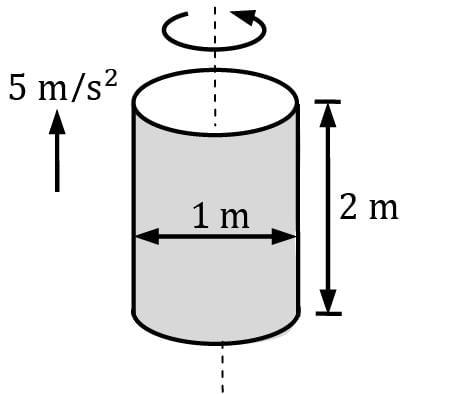
- a) 22 kPa and 8.2 kPa respectively
- b) 8.2 kPa and 22 kPa respectively
- c) 18.7 kPa and 11.2 kPa respectively
- d) 11.2 kPa and 18.7 kPa respectively
Correct answer is option 'A'. Can you explain this answer?
A 1-m-diameter, 2-m-high vertical cylinder is completely filled with gasoline whose density is 740 kg/m3. The tank is now rotated about its vertical axis at a rate of 90 rpm, while being accelerated upward at 5 m/s2. Determine
(i) the difference between the pressure at the centers of the bottom and top surfaces
(ii) the difference between the pressures at the center and the edge of the bottom surface.

a)
22 kPa and 8.2 kPa respectively
b)
8.2 kPa and 22 kPa respectively
c)
18.7 kPa and 11.2 kPa respectively
d)
11.2 kPa and 18.7 kPa respectively

|
Gate Funda answered |
Considering a small fluid element
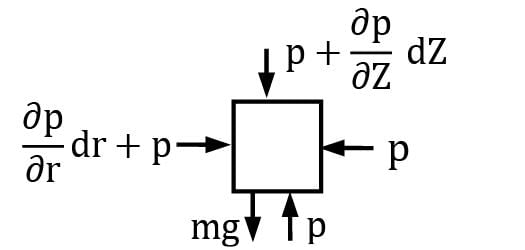
Resolving forces in z-direction, pdA − (p + ∂p / ∂z dz) dA − ρdAdzg = ρdAdz. a
⇒ − ∂p / ∂z dz = ρ(g + a)dz
Again resolving forces along r − (p + ∂p ∂r dr) dA + pdA + ρdAdrω2r = 0
[ρdAdrω2 r is the centrifugal force]
⇒∂p / ∂r dr = ρω2 rdr
Also we can write dp = ∂p / ∂r dr + ∂p / ∂z dz
∴ dp = ρω2rdr − ρ(a + g)dz
Which gives p = ρω2r2 / 2− ρ(a + g)z + C
(a) The difference of pressure at the center (r = 0) of top & bottom surface
Δp = Pbottom − Ptop
⇒ Δp = [−ρ(a + g)0 + C] − [−ρ(a + g)(2) + C]
⇒ Δp = ρ(a + g)(2)
⇒ Δp = 21.91 kPa
(b) The difference of pressure at the center and edge of bottom surface (Z = 0)
Δp = ρω2(0.5) 2/ 2
⇒ Δp = ρ × (N/60× 2π)2× (0.5)2 / 2
⇒ Δp = 8.21 kPa
An aluminium cube 150 mm on a side is suspended by a string in oil and water as shown in figure. The cube is submerged with half of it being in oil and the other half in water. Find the tension in the string if the specific gravity of oil is 0.8 and the specific weight of aluminium is 25.93 kN/m3 .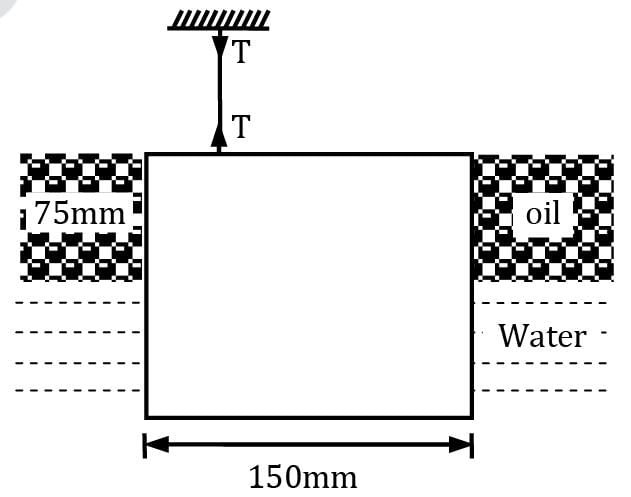 Correct answer is 'Range: 57.7 to 57.75'. Can you explain this answer?
Correct answer is 'Range: 57.7 to 57.75'. Can you explain this answer?
An aluminium cube 150 mm on a side is suspended by a string in oil and water as shown in figure. The cube is submerged with half of it being in oil and the other half in water. Find the tension in the string if the specific gravity of oil is 0.8 and the specific weight of aluminium is 25.93 kN/m3 .


|
Pioneer Academy answered |
At equilibrium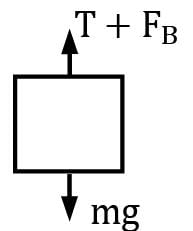

T + FB = mg
FB = FB,Oil + FB,water
FB = (0.8 × 103) × g × Vsolid / 2 + 103 × g × Vsolid / 2
FB = (400 + 500)g VSolid
FB = 900 g VSolid
T = mg − FB
T = (25.93 × 103 − 900 g)VSolid
T = 57.71 N
A hydraulic jack has the dimensions as shown. If one exerts a force F of 100 N on the handle of the jack, what load F2 (in kN) can the jack support? Neglect lifter weight.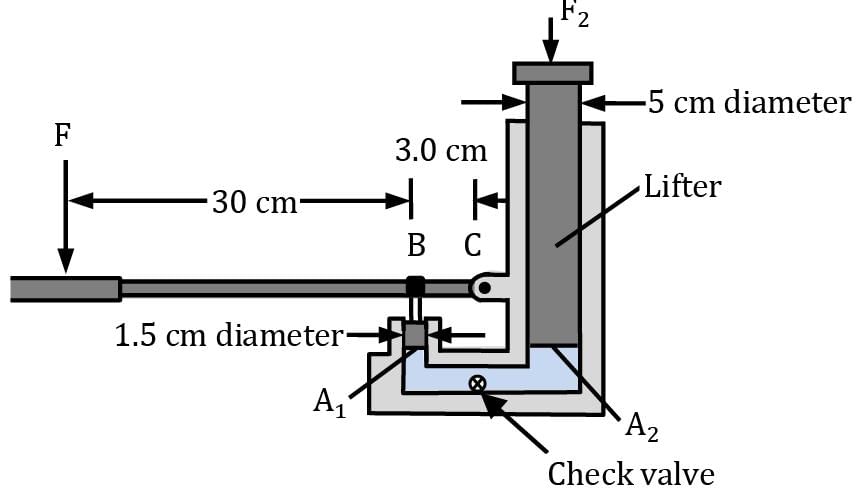 Correct answer is 'Range: 12.2 to 12.3'. Can you explain this answer?
Correct answer is 'Range: 12.2 to 12.3'. Can you explain this answer?
A hydraulic jack has the dimensions as shown. If one exerts a force F of 100 N on the handle of the jack, what load F2 (in kN) can the jack support? Neglect lifter weight.


|
Vertex Academy answered |
Using Pascal’s Law, any pressure change at any point in a confined fluid is transmitted equally throughout the fluid, without any loss.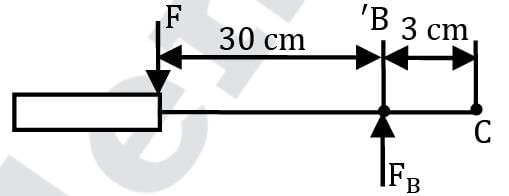
FB / A1 = F2 / A2 ⟹ FB × A2 / A1 = F2 ⋯ ①
rom FBD of handle

Equating Moments of F and FB about C
F × 33 = FB × 3
Or FB = F × 11 ⋯ ②
Using equation ① & ② and using
F = 100 N, d1 = 1.5 cm and d2 = 5 cm
We get, F2 = 12,222.22 N or 12.2 kN
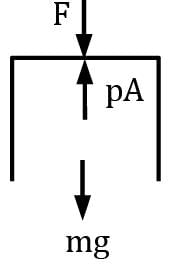
A cylindrical container whose weight is 79 N is inverted and pressed into the water, as shown in Figure. Determine the force F needed to hold the container at the position shown.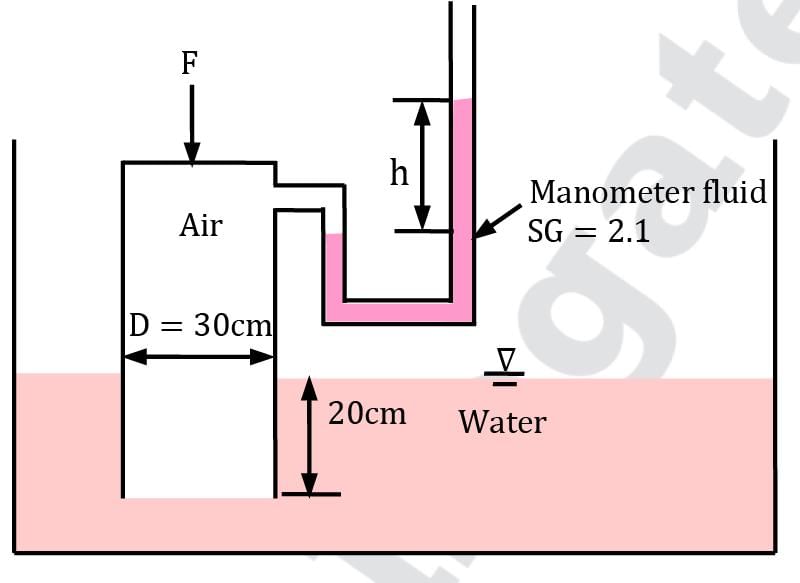 Correct answer is 'Range: 59 to 60'. Can you explain this answer?
Correct answer is 'Range: 59 to 60'. Can you explain this answer?
A cylindrical container whose weight is 79 N is inverted and pressed into the water, as shown in Figure. Determine the force F needed to hold the container at the position shown.

|
|
Sanya Agarwal answered |
At the same level in a static fluid, pressure is same everywhere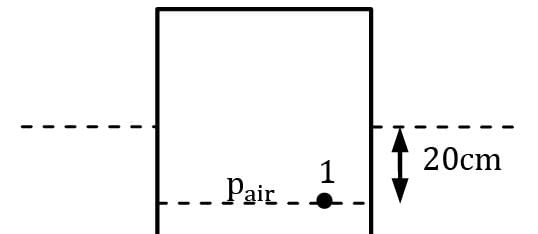

So p1 = ρw × g × 0.2 (Gauge Pressure)
(p1)Gauge = 1962 Pa
For calculating force on container

F = pA − mg
F = 1962 × π / 4 × (0.3)2 − 79
F = 59.68 N
Which of the following statements is correct regarding the center of pressure for a planar solid surface submerged in an incompressible fluid?- a) It always lies below the centroid of the surface. For a horizontal surface the two will coincide.
- b) It’s depth does not depend upon properties of fluid
- c) Deeper the surface goes in a liquid, closer the center of pressure moves towards the centroid
- d) All of the above
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is correct regarding the center of pressure for a planar solid surface submerged in an incompressible fluid?
a)
It always lies below the centroid of the surface. For a horizontal surface the two will coincide.
b)
It’s depth does not depend upon properties of fluid
c)
Deeper the surface goes in a liquid, closer the center of pressure moves towards the centroid
d)
All of the above
|
|
Sanya Agarwal answered |
Consider the expression for depth of center of pressure for a planar vertical surface.

hp = hc + IG /
Therefore
1. hp > hc, i. e. P lies below C
2. hp is independent of fluid density or Bulk Modulus. [This is not true if fluid is compressible
3. Also hp − hc = IG / Ahc
i. e. hc ↑ (hp − hc) ↓
Hence all these statements are correct and option (D) is the correct answer.
A 50-ton, 6-m-diameter hemispherical dome on a level surface is filled with water, as shown in figure. Someone claims that he can lift this dome by making use of Pascal’s law by attaching a long tube to the top and filling it with water. Determine the required height of water in the tube to lift the dome. Disregard the weight of the tube and the water in it.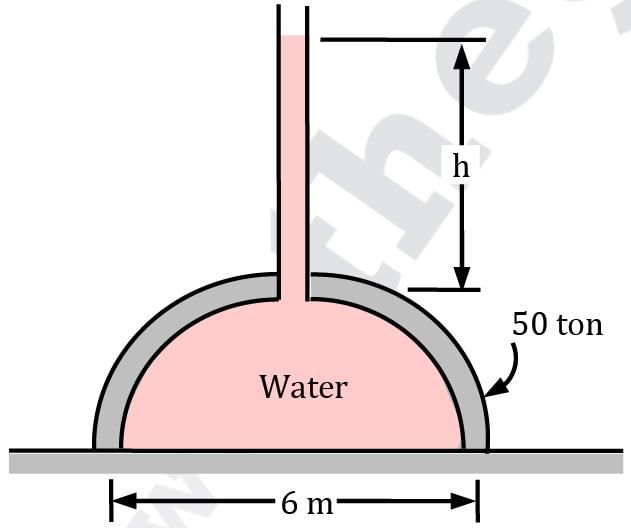 Common Data for Question No. 14 & 15 Consider two tumblers, A & B, initially empty. An ice block is placed in one of the tumblers, say A. Now slowly pour water in both the tumblers, such that the final water level is the same in the two.Correct answer is 'Range: 0.7 to 0.8'. Can you explain this answer?
Common Data for Question No. 14 & 15 Consider two tumblers, A & B, initially empty. An ice block is placed in one of the tumblers, say A. Now slowly pour water in both the tumblers, such that the final water level is the same in the two.Correct answer is 'Range: 0.7 to 0.8'. Can you explain this answer?
A 50-ton, 6-m-diameter hemispherical dome on a level surface is filled with water, as shown in figure. Someone claims that he can lift this dome by making use of Pascal’s law by attaching a long tube to the top and filling it with water. Determine the required height of water in the tube to lift the dome. Disregard the weight of the tube and the water in it.

Common Data for Question No. 14 & 15 Consider two tumblers, A & B, initially empty. An ice block is placed in one of the tumblers, say A. Now slowly pour water in both the tumblers, such that the final water level is the same in the two.
|
|
Sanya Agarwal answered |
The hydrostatic force on the dome can be calculated by weight of the virtual fluid considered upto free surface.

FHS = [π /4× d2 × (h + 3) − 2 /3 πr3] × ρW × g
To lift the dome FHS = mg
So,
[28.27(h + 3) − 56.54]ρW × g = 50 × 103 × g
28.27 (h + 3) = 106.54
h + 3 = 3.768
h = 0.77 m
An inclined tube manometer measures the gauge pressure ps of a system S (Fig.). The reservoir and tube diameters of the manometer are 50 mm and 5 mm respectively. The inclination angle of the tube is 30°. What will be the percentage error in measuring Ps if the reservoir deflection is neglected?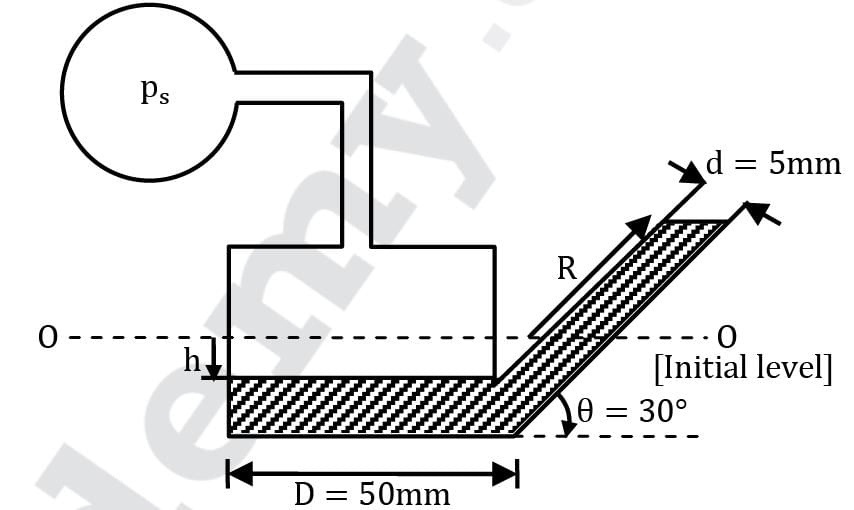 Correct answer is 'Range: 1.96 to 1.96'. Can you explain this answer?
Correct answer is 'Range: 1.96 to 1.96'. Can you explain this answer?
An inclined tube manometer measures the gauge pressure ps of a system S (Fig.). The reservoir and tube diameters of the manometer are 50 mm and 5 mm respectively. The inclination angle of the tube is 30°. What will be the percentage error in measuring Ps if the reservoir deflection is neglected?


|
Gate Funda answered |
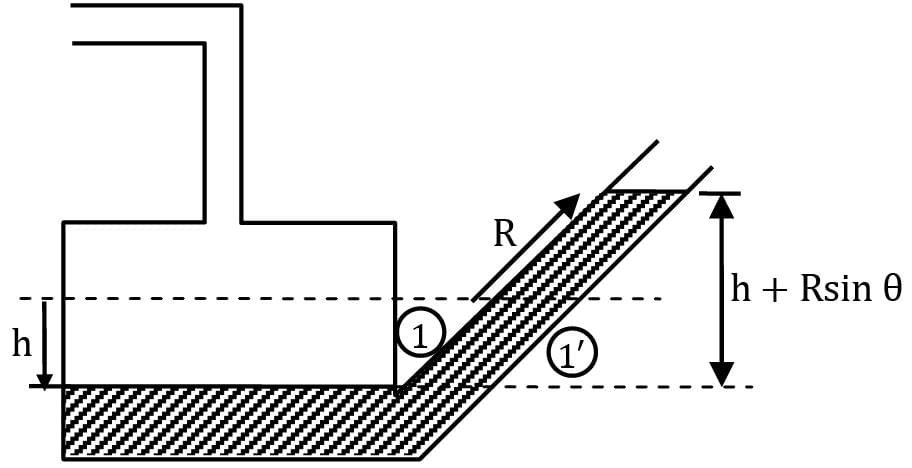
Equating pressure values at 1 and 1′
P1 = P1′
P1 = ρg(h + R sin θ) ⋯ ①
By mass conservation Ah = aR
π 4 / D2 h = π 4 / d2R
h / R = d2 / D2
h / R = (5 / 50)2
h / R= 0.01
If h term is neglected in ① as h ≪ R
P1 ≃ ρgR sin θ
which will be an approximate value of P1
∴ Error = Exact − Approximate
% Error = Exact − Approximate / Exact × 100
% Error = ρg(h + R sin θ) − ρgR sin θ / ρg(h + R sin θ) × 100
% Error = h / h + R sin θ × 100
% Error = 1 / 1 +R / h sin θ × 100
% Error = 1 / 1 + 100 ×1 / 2 × 100
% Error = 1.96%
Gauge pressure at a point is equal to- a)absolute pressure plus atmospheric pressure
- b)absolute pressure minus atmospheric pressure
- c)vacuum pressure plus absolute pressure
- d)vacuum pressure minus absolute pressure
Correct answer is option 'B'. Can you explain this answer?
Gauge pressure at a point is equal to
a)
absolute pressure plus atmospheric pressure
b)
absolute pressure minus atmospheric pressure
c)
vacuum pressure plus absolute pressure
d)
vacuum pressure minus absolute pressure
|
|
Nandini Basak answered |
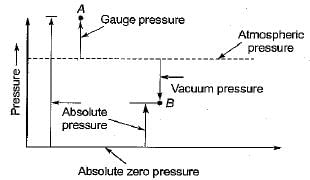
∴ Gauge pressure = Absolute minus atmospheric pressure
A Differential manometer is connected at the points A and Bat the centre of two pipes. The pipe A(left limb) contains a liquid of specific gravity = 1.5 while pipe B (right limb)contains a liquid of specific gravity 0.85. The pressure at A and B are .5 kgf/cm2 and 1.2 kgf/cm2 respectively. Find the difference in level of mercuru in the differential manometer. A is 2.5m above B and 5 m above the mercury in its own limb. B is 2.5 m above the mercury level in limb A.- a)12.7 cm
- b)25.5 cm
- c)6.28 cm
- d)10.85 cm
Correct answer is option 'A'. Can you explain this answer?
A Differential manometer is connected at the points A and Bat the centre of two pipes. The pipe A(left limb) contains a liquid of specific gravity = 1.5 while pipe B (right limb)contains a liquid of specific gravity 0.85. The pressure at A and B are .5 kgf/cm2 and 1.2 kgf/cm2 respectively. Find the difference in level of mercuru in the differential manometer. A is 2.5m above B and 5 m above the mercury in its own limb. B is 2.5 m above the mercury level in limb A.
a)
12.7 cm
b)
25.5 cm
c)
6.28 cm
d)
10.85 cm

|
Aditi Chakraborty answered |
Explanation: Total pressure at the datum line in limb A = Total pressure at the datum line in limb B\
0.5*9.81*10000 + 5*9.81*1500 + h*9.81*13600 = 1.2*9.81*10000 + (h+2)*9.81*850
After solving,
h=12.7 cm.
0.5*9.81*10000 + 5*9.81*1500 + h*9.81*13600 = 1.2*9.81*10000 + (h+2)*9.81*850
After solving,
h=12.7 cm.
We can draw Mohr’s circle for a fluid at rest.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
We can draw Mohr’s circle for a fluid at rest.
a)
True
b)
False

|
Aarav Kulkarni answered |
Explanation: Mohr’s circle is used to denote shear stress distribution. For fluid at rest, there is no shear stress. Hence, we cannot draw Mohr’s circle for fluid at rest.
An elastic air balloon having a diameter of 30 cm is attached to the base of a container partially filled with water at +4°C, as shown in Figure. If the pressure of air above water is gradually increased from 100 kPa to 1.6 MPa, will the force on the cable change? If so, what is the percent change in the force? Assume the pressure on the free surface and the diameter of the balloon are related by p = CDn , where C is a constant and n = −2. The weight of the balloon and the air in it is negligible.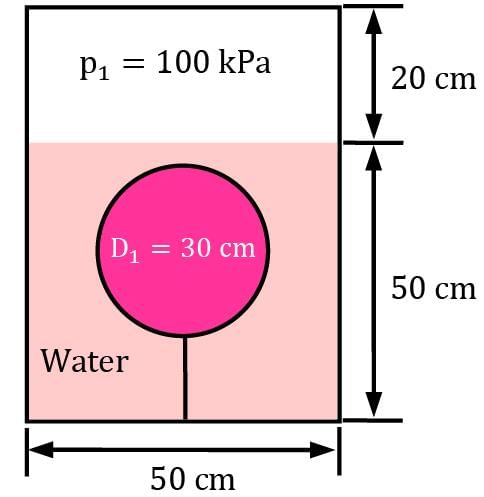 Correct answer is 'Range: 98 to 99'. Can you explain this answer?
Correct answer is 'Range: 98 to 99'. Can you explain this answer?
An elastic air balloon having a diameter of 30 cm is attached to the base of a container partially filled with water at +4°C, as shown in Figure. If the pressure of air above water is gradually increased from 100 kPa to 1.6 MPa, will the force on the cable change? If so, what is the percent change in the force? Assume the pressure on the free surface and the diameter of the balloon are related by p = CDn , where C is a constant and n = −2. The weight of the balloon and the air in it is negligible.

|
|
Sanvi Kapoor answered |
FBD of balloon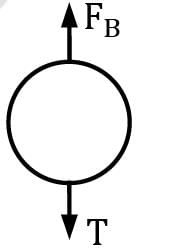

where FB = Buoyant force T = Tension Clearly T = FB
As the balloon is flexible, and as the pressure changes, the volume of the balloon will also change, so will the buoyant force experienced by it. So
FB1 = ρ × 4 / 3 πr13 × g and FB2 = ρ × 4 / 3 πr23 × g
Given, p = C / D2 ⟹ D = √C / p
⇒ r1 = 1 / 2√ C / p1 and r2 = 1 / 2 √C / p2
% change in Buoyant force
=FB2 − FB1 / FB1× 100
= (FB2 / FB1− 1) × 100
= [(p1 / p2)3/2 − 1] × 100
Putting p1 = 100 kPa and p2 = 1.6 kPa we get the % change in Buoyant Force = −98.4%.
The negative sign indicates that Buoyant Force decreases.
A house-top water tank is made of flat plates and is full to the brim. Its height is twice that of any side. The ratio of total thrust force on the bottom of the tank to that on any side will be- a) 4
- b) 2
- c) 1
- d) 0.5
Correct answer is option 'B'. Can you explain this answer?
A house-top water tank is made of flat plates and is full to the brim. Its height is twice that of any side. The ratio of total thrust force on the bottom of the tank to that on any side will be
a)
4
b)
2
c)
1
d)
0.5

|
Bhaskar Unni answered |
Given information:
- The house-top water tank is made of flat plates.
- The tank is full to the brim.
- The height of the tank is twice that of any side.
To find:
The ratio of total thrust force on the bottom of the tank to that on any side.
Solution:
1. Understanding the concept of thrust force:
Thrust force is the force exerted by a fluid (in this case, water) on a surface due to the pressure exerted by the fluid. The thrust force is always perpendicular to the surface.
2. Analysis of the tank:
Since the tank is full to the brim, the water exerts pressure on all the surfaces of the tank, including the bottom and the sides. Let's consider a rectangular tank for easier analysis.
3. Thrust force on the bottom of the tank:
The thrust force on the bottom of the tank is equal to the pressure exerted by the water multiplied by the area of the bottom surface. Since the tank is full to the brim, the pressure at the bottom is the same as the pressure at any other point inside the tank. Therefore, the thrust force on the bottom is equal to the pressure multiplied by the area of the bottom surface.
4. Thrust force on any side of the tank:
The thrust force on any side of the tank is equal to the pressure exerted by the water multiplied by the area of that side. The pressure at any point on the side is equal to the pressure at the same height inside the tank. Therefore, the thrust force on any side is equal to the pressure multiplied by the area of that side.
5. Comparison of thrust forces:
Let's assume the length of the tank is L, the width is W, and the height is H. According to the given information, H = 2W.
- Thrust force on the bottom: Pressure x Area of bottom = Pressure x (L x W)
- Thrust force on any side: Pressure x Area of side = Pressure x (L x H)
Since H = 2W, the thrust force on any side becomes Pressure x (L x 2W) = Pressure x (2LW) = 2 x (Pressure x LW)
6. Ratio of thrust forces:
The ratio of total thrust force on the bottom of the tank to that on any side can be calculated as follows:
Total thrust force on the bottom / Thrust force on any side = (Pressure x (L x W)) / (2 x (Pressure x LW))
The pressure cancels out, as it is the same for both cases. Similarly, the length (L) cancels out.
Therefore, the ratio simplifies to:
Total thrust force on the bottom / Thrust force on any side = W / (2W) = 1/2 = 0.5
Conclusion:
The ratio of the total thrust force on the bottom of the tank to that on any side is 0.5, which corresponds to option (B).
- The house-top water tank is made of flat plates.
- The tank is full to the brim.
- The height of the tank is twice that of any side.
To find:
The ratio of total thrust force on the bottom of the tank to that on any side.
Solution:
1. Understanding the concept of thrust force:
Thrust force is the force exerted by a fluid (in this case, water) on a surface due to the pressure exerted by the fluid. The thrust force is always perpendicular to the surface.
2. Analysis of the tank:
Since the tank is full to the brim, the water exerts pressure on all the surfaces of the tank, including the bottom and the sides. Let's consider a rectangular tank for easier analysis.
3. Thrust force on the bottom of the tank:
The thrust force on the bottom of the tank is equal to the pressure exerted by the water multiplied by the area of the bottom surface. Since the tank is full to the brim, the pressure at the bottom is the same as the pressure at any other point inside the tank. Therefore, the thrust force on the bottom is equal to the pressure multiplied by the area of the bottom surface.
4. Thrust force on any side of the tank:
The thrust force on any side of the tank is equal to the pressure exerted by the water multiplied by the area of that side. The pressure at any point on the side is equal to the pressure at the same height inside the tank. Therefore, the thrust force on any side is equal to the pressure multiplied by the area of that side.
5. Comparison of thrust forces:
Let's assume the length of the tank is L, the width is W, and the height is H. According to the given information, H = 2W.
- Thrust force on the bottom: Pressure x Area of bottom = Pressure x (L x W)
- Thrust force on any side: Pressure x Area of side = Pressure x (L x H)
Since H = 2W, the thrust force on any side becomes Pressure x (L x 2W) = Pressure x (2LW) = 2 x (Pressure x LW)
6. Ratio of thrust forces:
The ratio of total thrust force on the bottom of the tank to that on any side can be calculated as follows:
Total thrust force on the bottom / Thrust force on any side = (Pressure x (L x W)) / (2 x (Pressure x LW))
The pressure cancels out, as it is the same for both cases. Similarly, the length (L) cancels out.
Therefore, the ratio simplifies to:
Total thrust force on the bottom / Thrust force on any side = W / (2W) = 1/2 = 0.5
Conclusion:
The ratio of the total thrust force on the bottom of the tank to that on any side is 0.5, which corresponds to option (B).
The total pressure or pressure intensity is zero for any point on inclined surface in space.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
The total pressure or pressure intensity is zero for any point on inclined surface in space.
a)
True
b)
False

|
Navya Saha answered |
Explanation: Total pressure, F=w*a*ŷ
In space, w=0 as g=0
Hence, f=0.
In space, w=0 as g=0
Hence, f=0.
The 4-m–diameter circular gate of the figure is located in the incline wall of a large reservoir containing water (γ = 9.80 kN/m3). The gate is mounted on a shaft along its horizontal diameter, and the water depth is 10 m above the shaft. Determine the moment in kN-m that would have to be applied to the shaft to open the gate.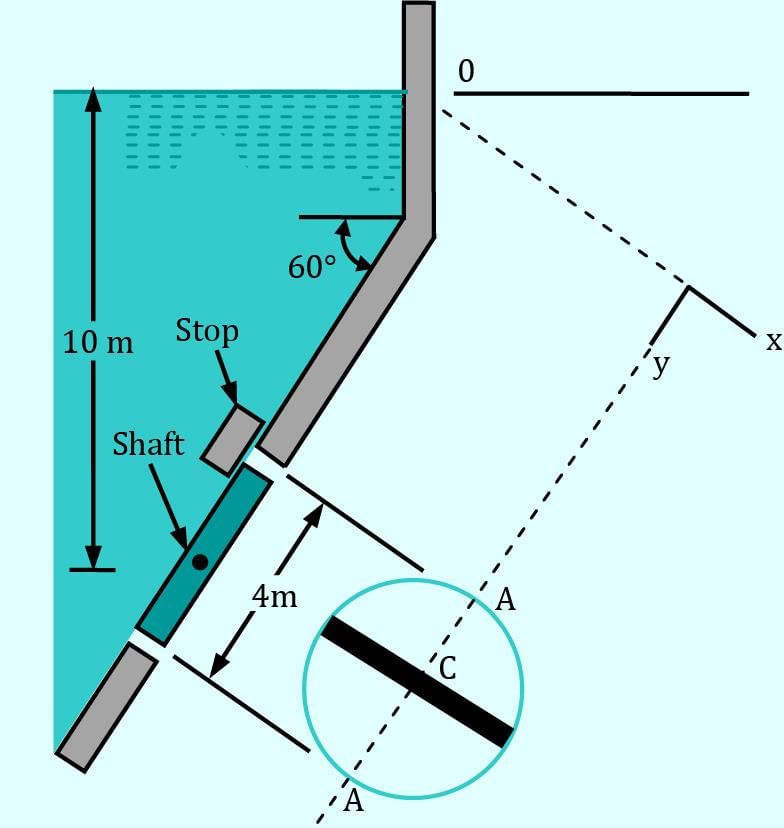 Correct answer is 'Range: 98 to 99'. Can you explain this answer?
Correct answer is 'Range: 98 to 99'. Can you explain this answer?
The 4-m–diameter circular gate of the figure is located in the incline wall of a large reservoir containing water (γ = 9.80 kN/m3). The gate is mounted on a shaft along its horizontal diameter, and the water depth is 10 m above the shaft. Determine the moment in kN-m that would have to be applied to the shaft to open the gate.

|
|
Sanya Agarwal answered |
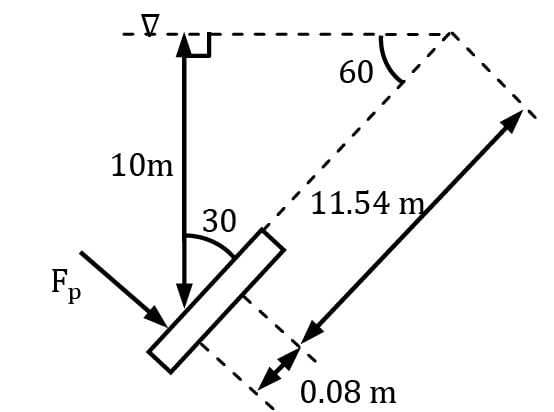
Hydrostatic forces on the circular gate
= ρ × g × hC × Area
= 103 × g × 10 × π / 4× 42
= 1232.76 kN
yP = IxC / A × yC + yC = πD4 /64 /π 4D2 × 11.54 + 11.54
= 11.62 m
(Note: this is ?? and not the depth from free surface)
Fp = 1232.76 kN acts 0.08 m Below the centroid, measured along the plane of the gate The moment required to turn the gate about the shaft = Fp × (yp − yc)
= 1232.76 × (11.62 − 11.54) × 103
= 98.62 kN-m
In case of spherical bodies with uniform mass distribution, what is the position of center of pressure relative to centre of gravity.- a)Above
- b)Below
- c)Coincides
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
In case of spherical bodies with uniform mass distribution, what is the position of center of pressure relative to centre of gravity.
a)
Above
b)
Below
c)
Coincides
d)
None of the mentioned

|
Anuj Chakraborty answered |
Explanation: In case of spherical bodies with uniform mass distribution, centre of pressure coincides with centre of gravity.
Consider a U-tube filled with mercury except the 18-cm-high portion at the top, as shown in figure. The diameter of the right arm of theU-tube is D = 2 cm, and the diameter of the left arm is 2D. Oil with a specific gravity of 2.72 is poured into the left arm, forcing some mercury from the left arm into the right one. Determine the maximum amount of oil in liters that can be added into the left arm. Correct answer is 'Range: 0.23 to 0.24'. Can you explain this answer?
Correct answer is 'Range: 0.23 to 0.24'. Can you explain this answer?
Consider a U-tube filled with mercury except the 18-cm-high portion at the top, as shown in figure. The diameter of the right arm of theU-tube is D = 2 cm, and the diameter of the left arm is 2D. Oil with a specific gravity of 2.72 is poured into the left arm, forcing some mercury from the left arm into the right one. Determine the maximum amount of oil in liters that can be added into the left arm.


|
Vertex Academy answered |
When oil is poured in left limb, the level of mercury goes down by h1 and in right limb goes up by h2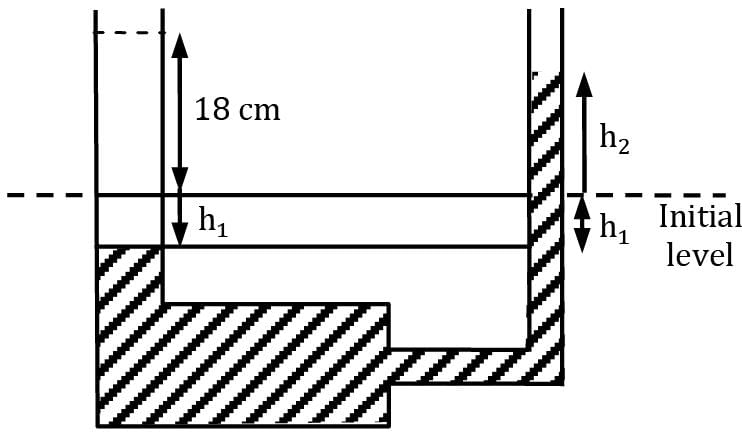

After adding the oil, ρoil × g(18 + h1) = ρHg × g(h1 + h2)
2.72 × (18 + h1) = 13.6 (h1 + h2)
Also h1 × (2D)2 = D2 × h2
h1 × 4 = h2
2.72 × (18 + h1) = 13.6(5h1)
48.96 + 2.72 h1 = 68 h1
h1 = 0.75 cm
Quantity of oil added
=π / 4 × (0.04)2 × (0.1875
= 2.35 × 102-4m3
= 0.2356 lts.
Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?Correct answer is 'Range: 196 to 197'. Can you explain this answer?
Consider a tank of length 20 cm and unit width perpendicular to a plane of paper filled with water upto a height of 10 cm. The tank starts moving with a constant acceleration along a horizontal direction such that the level of water in the front goes down by 10 cm. What is the force acting on the rear end of the container?

|
Gate Gurus answered |
In such cases fall of water level in front is same as rise of water in rear. Hence when container is moving the situation is as such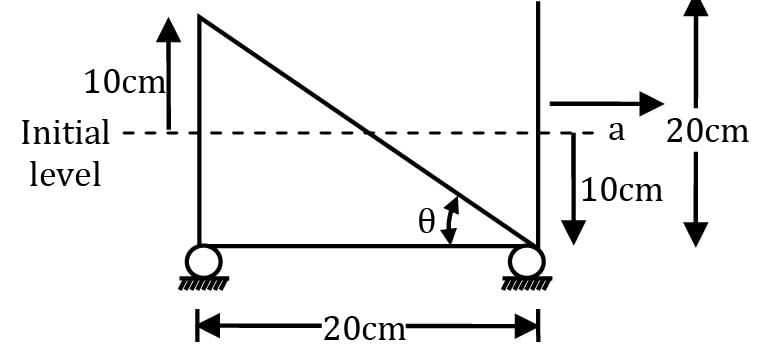

tan θ = a / g
⇒20 / 20 = a / g
⇒ a = g
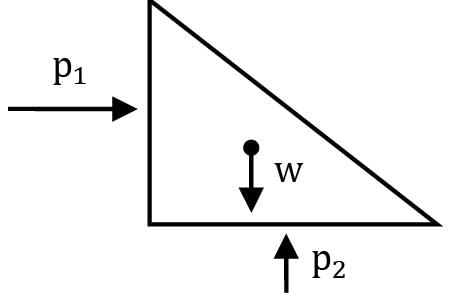
Consider FBD of water body

∴ where p1 and p2 are pressure forces exerted by rear end and bottom of container.
Therefore p1 = ma = ρVa
= 1000 × (0.1 × 0.2 × 1) × 9.81
= 196.2 N
An inverted differential manometer is connected to two pipes A and B which covey water. The fluid in manometer is oil of specific gravity 0.75. For the manometer readings, find the pressure difference between A and B. Datum in left limb is 40 cm above point A. Point B is 60 cm below datum line. Difference in level of fluid is 20 cm.
- a)1471 N/m2
- b)2943 N/m2
- c)735.75 N/m2
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
An inverted differential manometer is connected to two pipes A and B which covey water. The fluid in manometer is oil of specific gravity 0.75. For the manometer readings, find the pressure difference between A and B. Datum in left limb is 40 cm above point A. Point B is 60 cm below datum line. Difference in level of fluid is 20 cm.
a)
1471 N/m2
b)
2943 N/m2
c)
735.75 N/m2
d)
None of the mentioned

|
Rounak Saini answered |
Explanation: Total pressure at the datum line in limb A = Total pressure at the datum line in limb B
Pressure difference between A and B = -0.4*9.81*1000 + 0.2*9.81*750 + 0.4*9.81*1000
= 1471 N/m2.
Pressure difference between A and B = -0.4*9.81*1000 + 0.2*9.81*750 + 0.4*9.81*1000
= 1471 N/m2.
An open tank contains water upto a depth of 350 cm and above it an oil of specific gravity 0.65 for a depth of 2.5 m. Find the pressure intensity at the extreme bottom of the tank. - a)5.027 N/cm2
- b)10.05 N/cm2
- c)2.51 N/cm2
- d)None of the mentioned
Correct answer is option 'A'. Can you explain this answer?
An open tank contains water upto a depth of 350 cm and above it an oil of specific gravity 0.65 for a depth of 2.5 m. Find the pressure intensity at the extreme bottom of the tank.
a)
5.027 N/cm2
b)
10.05 N/cm2
c)
2.51 N/cm2
d)
None of the mentioned

|
Samarth Ghoshal answered |
Given:
Depth of water (h1) = 350 cm
Depth of oil (h2) = 250 cm
Specific gravity of oil (γ) = 0.65
To find: Pressure intensity at the extreme bottom of the tank
Assumptions:
1. The density of water is constant and equal to 1000 kg/m³.
2. The density of oil is constant and equal to 0.65*1000 = 650 kg/m³.
3. The pressure at any point in the liquid is equal in all directions.
4. The atmospheric pressure is negligible.
Calculation:
1. Total depth of liquid (h) = h1 + h2 = 600 cm = 6 m
2. Pressure at the bottom of the tank is given by the formula, P = ρgh, where ρ is the density of liquid, g is the acceleration due to gravity, and h is the depth of liquid.
3. Pressure at the bottom of the water layer (P1) = ρ1*g*h1, where ρ1 is the density of water = 1000 kg/m³.
=> P1 = 1000*9.81*3.5 = 34350 Pa
4. Pressure at the bottom of the oil layer (P2) = ρ2*g*h2, where ρ2 is the density of oil = 650 kg/m³.
=> P2 = 650*9.81*2.5 = 16001.25 Pa
5. Total pressure at the bottom of the tank (P) = P1 + P2
=> P = 34350 + 16001.25 = 50351.25 Pa
6. Pressure intensity = P/10000 (converting Pa to N/cm²)
=> Pressure intensity = 50351.25/10000 = 5.027 N/cm²
Therefore, the pressure intensity at the extreme bottom of the tank is 5.027 N/cm², which is closest to option A (5.027 N/cm²).
Depth of water (h1) = 350 cm
Depth of oil (h2) = 250 cm
Specific gravity of oil (γ) = 0.65
To find: Pressure intensity at the extreme bottom of the tank
Assumptions:
1. The density of water is constant and equal to 1000 kg/m³.
2. The density of oil is constant and equal to 0.65*1000 = 650 kg/m³.
3. The pressure at any point in the liquid is equal in all directions.
4. The atmospheric pressure is negligible.
Calculation:
1. Total depth of liquid (h) = h1 + h2 = 600 cm = 6 m
2. Pressure at the bottom of the tank is given by the formula, P = ρgh, where ρ is the density of liquid, g is the acceleration due to gravity, and h is the depth of liquid.
3. Pressure at the bottom of the water layer (P1) = ρ1*g*h1, where ρ1 is the density of water = 1000 kg/m³.
=> P1 = 1000*9.81*3.5 = 34350 Pa
4. Pressure at the bottom of the oil layer (P2) = ρ2*g*h2, where ρ2 is the density of oil = 650 kg/m³.
=> P2 = 650*9.81*2.5 = 16001.25 Pa
5. Total pressure at the bottom of the tank (P) = P1 + P2
=> P = 34350 + 16001.25 = 50351.25 Pa
6. Pressure intensity = P/10000 (converting Pa to N/cm²)
=> Pressure intensity = 50351.25/10000 = 5.027 N/cm²
Therefore, the pressure intensity at the extreme bottom of the tank is 5.027 N/cm², which is closest to option A (5.027 N/cm²).
For an inclined plane for which position, maximum total pressure acts on it.- a)Horizontal
- b)Vertical
- c)Inclined
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
For an inclined plane for which position, maximum total pressure acts on it.
a)
Horizontal
b)
Vertical
c)
Inclined
d)
None of the mentioned

|
Anuj Chakraborty answered |
Explanation: Total pressure, F=w*a*ŷ=w*A*(y+dsinθ)
For vertical plate, θ=90⁰
Hence, total pressure is maximum.
For vertical plate, θ=90⁰
Hence, total pressure is maximum.
Figure shows a conical vessel having its outlet at A to which a U-tube manometer is connected. The reading of the manometer indicated in the figure pertains to the situation when the vessel is empty, i.e. the water surface is at A. Find the reading of the manometer when the vessel is completely filled with water.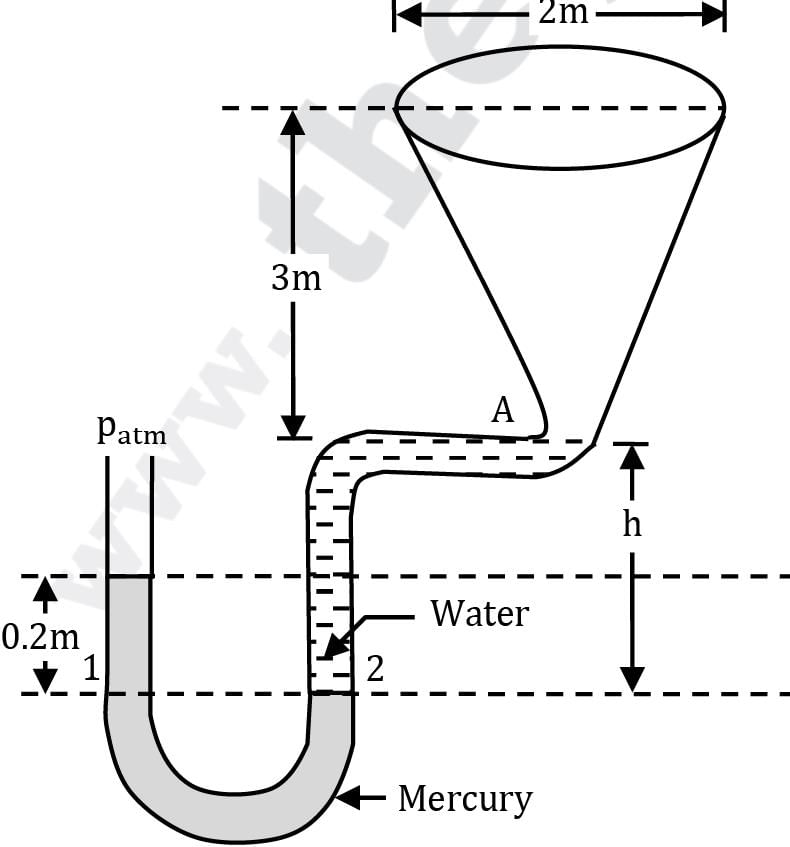 Correct answer is 'Range: 42 to 44'. Can you explain this answer?
Correct answer is 'Range: 42 to 44'. Can you explain this answer?
Figure shows a conical vessel having its outlet at A to which a U-tube manometer is connected. The reading of the manometer indicated in the figure pertains to the situation when the vessel is empty, i.e. the water surface is at A. Find the reading of the manometer when the vessel is completely filled with water.


|
Vertex Academy answered |
Case (a) when the vessel is empty Equating pressure values at the points 1 and 2 which lie at the same horizontal plane; patm + (13.6 × 9810 × 0.2) = 9810 × h + Patm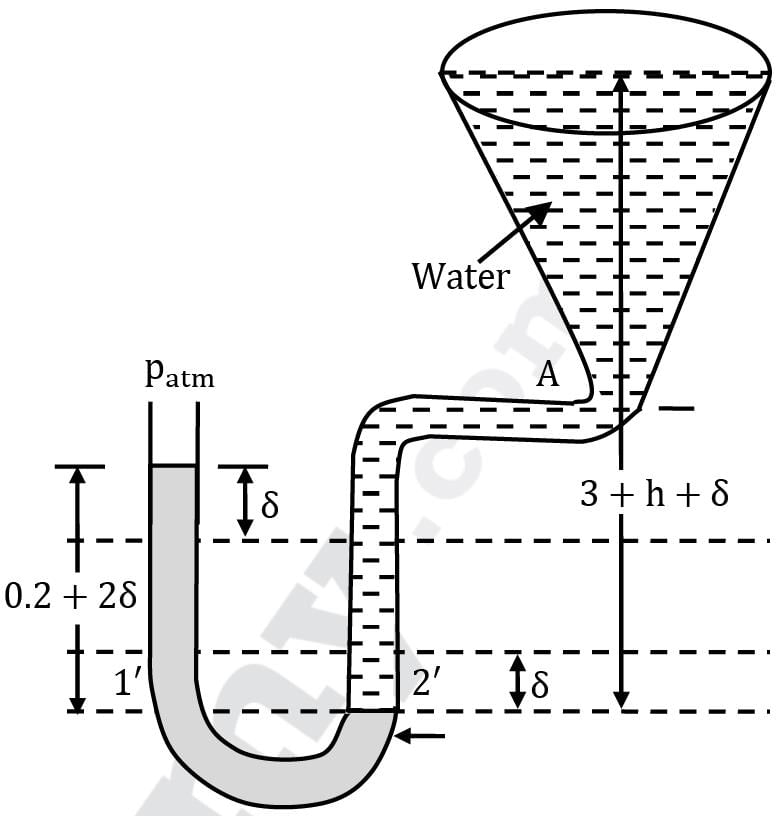
∴ h = 13.6 × 9810 × 0.2 / 9810
= 2.72 m

For case (b) when the vessel is full of water: Let the mercury level fall by a distance δ in the right limb with a corresponding rise δ in the left limb. Again writing the governing manometric equation for the points 1′ and 2′:
Patm + 13.6 × 9810 × (0.2 + 2δ)
= 9810 (3 + 2.72 + δ) + Patm
Solution gives: δ = 0.1145 m Hence the manometer reading would be
0.20 + 2 × 0.1145 = 0.429 m
= 42.90 cm
The distance between the centers of the two arms of a U-tube open to the atmosphere is 25 cm, and the U-tube contains 20-cm-high alcohol in both arms. Now the U-tube is rotated about the left arm at 4.2 rad/s. Determine the elevation difference between the fluid surfaces in the two arms.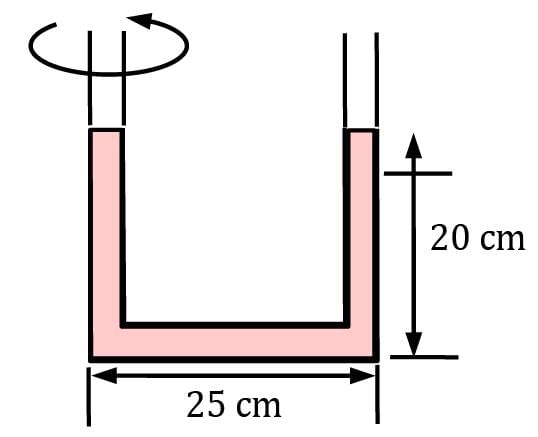 Correct answer is 'Range: 5.6 to 5.7'. Can you explain this answer?
Correct answer is 'Range: 5.6 to 5.7'. Can you explain this answer?
The distance between the centers of the two arms of a U-tube open to the atmosphere is 25 cm, and the U-tube contains 20-cm-high alcohol in both arms. Now the U-tube is rotated about the left arm at 4.2 rad/s. Determine the elevation difference between the fluid surfaces in the two arms.


|
Vertex Academy answered |
When the U-Tube will rotate

p1 = p2 = patm For forced vortex
p = ρω2r2 / 2 − ρgZ + C
Equating pressures at 1 & 2
ρω2(0)2 /2− ρg(0) = ρω2r2/2 /2 − ρgh
i. e ω2r2/2 / 2 = gh
(4.2)2(0.25)2 /2 = gh
h = 5.61 cm
Which of the following options represents the variation of pressure with altitude in an isothermal atmosphere? The symbols have the usual meanings.- a) p = po e −gy / RT
- b) p = po e gy / RT
- c) p = po (1 + By / To) g / RB
- d) p = p0 (1 − By / To)g / RB
Correct answer is option 'A'. Can you explain this answer?
Which of the following options represents the variation of pressure with altitude in an isothermal atmosphere? The symbols have the usual meanings.
a)
p = po e −gy / RT
b)
p = po e gy / RT
c)
p = po (1 + By / To) g / RB
d)
p = p0 (1 − By / To)g / RB
|
|
Sanya Agarwal answered |
We know dp / dy = −ρg
For ideal gas, PV = mRT or p = ρRT
∴ ρ = p / RT
Substituting value of ρ
dp / dy = −p / RT × g
⇒ dp / p = −g / RTdy
⟹ ln p = −g / RTy + C
or p = C e −gy / RT
Also at zero scale level, i.e.

!t y = 0, p = p0
⇒ p0 = C
Substituting the same
p = p0 e −gy / RT
A big container filled with water and oil (S = 0.6) is shown in the figure.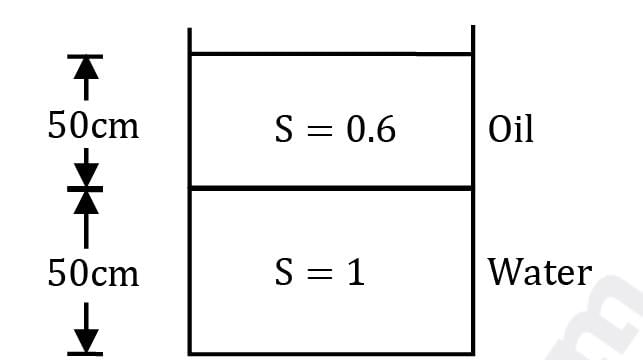 A vertical cylinder of density 900 kg/m3 and height 10 cm is dropped in the container. Which of the following options is correct?
A vertical cylinder of density 900 kg/m3 and height 10 cm is dropped in the container. Which of the following options is correct?- a) The cylinder will float at the top
- b) It will sink to bottom
- c) It will stay at interface with 2.5 cm length in oil
- d) It will stay at interface with 7.5 cm length in interface
Correct answer is option 'C'. Can you explain this answer?
A big container filled with water and oil (S = 0.6) is shown in the figure.

A vertical cylinder of density 900 kg/m3 and height 10 cm is dropped in the container. Which of the following options is correct?
a)
The cylinder will float at the top
b)
It will sink to bottom
c)
It will stay at interface with 2.5 cm length in oil
d)
It will stay at interface with 7.5 cm length in interface
|
|
Sanya Agarwal answered |
As the density of the cylinder is more than oil it will sink for oil but float for water. Hence in equilibrium condition, the cylinder will stay at the interface of water and oil.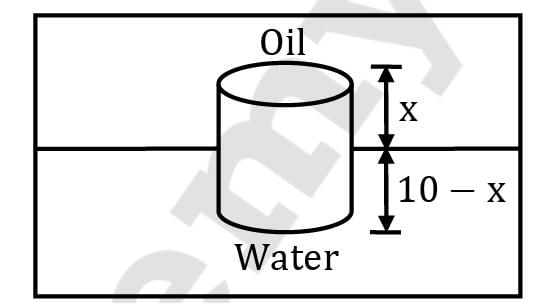
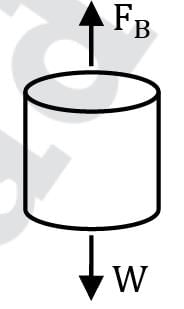

Consider FBD of cylinder

W = FB
W = FB,Oil + FB,Water
W = ρ0Vd0g + ρwVdwg
ρbVbg = ρ0Vd0g + ρwVdwg
900 × A × 10 = 600 × A × x + 1000 × A(10 − x)
9000 = 600 x + 10000 − 1000 x
∴ −1000 = −400 x
x = 1000 / 400
x = 2.5 cm
For dynamic fluid motion in a pipe, the pressure measurement cannot be carried out accurately by manometer.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
For dynamic fluid motion in a pipe, the pressure measurement cannot be carried out accurately by manometer.
a)
True
b)
False

|
Sameer Verma answered |
Accuracy of Pressure Measurement in Dynamic Fluid Motion
Pressure measurement in a pipe with dynamic fluid motion cannot be accurately carried out by a manometer due to several reasons.
Fluid Velocity
- In dynamic fluid motion, the fluid velocity is constantly changing, causing fluctuations in pressure.
- Manometers are designed for static pressure measurements and may not provide accurate readings in dynamic fluid systems.
Response Time
- Manometers have a slower response time compared to other pressure measurement devices.
- In dynamic fluid systems, quick and precise pressure measurements are essential, which may not be possible with a manometer.
Accuracy
- Manometers may not be able to accurately capture the true pressure values in a dynamic system due to the rapid changes in fluid flow.
- The readings obtained from a manometer may not reflect the actual pressure conditions in the pipe.
Recommendation
- In dynamic fluid systems, it is recommended to use pressure transducers or other specialized instruments that are designed to handle rapid changes in pressure.
- These devices provide more accurate and reliable pressure measurements in dynamic fluid motion scenarios.
In conclusion, while manometers are useful for static pressure measurements, they may not be suitable for accurately measuring pressure in pipes with dynamic fluid motion. It is important to use appropriate instruments that can handle the unique challenges posed by dynamic fluid systems.
For the stability of a floating body, which of the following is true?- a) Metacenter should be below the center of gravity
- b) Metacenter should be above the center of gravity
- c) Metacenter and center of gravity must lie on the same horizontal line
- d) Metacenter and center of gravity must lie on the same vertical line
Correct answer is option 'B'. Can you explain this answer?
For the stability of a floating body, which of the following is true?
a)
Metacenter should be below the center of gravity
b)
Metacenter should be above the center of gravity
c)
Metacenter and center of gravity must lie on the same horizontal line
d)
Metacenter and center of gravity must lie on the same vertical line
|
|
Sanya Agarwal answered |
Consider a floating body initially in equilibrium. When this body is given a rotational displacement, the centre of buoyancy (B) shall shift to B′.


1-1 is the initial line of action of buoyant force.
And Metacenter (M) is the intersection of 1-1 with the new line of action [After displacement].

As is seen the displacement of B to B′ generates a couple opposite to displacement and thus restores the body to initial equilibrium position.
In this case M lies above G.
But in other cases when M lies below G, the couple is over turning and the body is unstable.
The density in a liquid varies as ρ(h) = 400 + 10h kg/m3 where ρ is the density at a point h meters below the free surface. Find out pressure at a point 8 m below the free surface.- a) 37.67 kPa
- b) 31.392 kPa
- c) 34.531 kPa
- d) None of the above
Correct answer is option 'C'. Can you explain this answer?
The density in a liquid varies as ρ(h) = 400 + 10h kg/m3 where ρ is the density at a point h meters below the free surface. Find out pressure at a point 8 m below the free surface.
a)
37.67 kPa
b)
31.392 kPa
c)
34.531 kPa
d)
None of the above
|
|
Sanya Agarwal answered |
In this case, the equation p = p0 + ρgh is not applicable as the fluid is compressible.
Therefore using hydro-static law
dp / dh = ρg
dp / dh = (400 + 10h)g dp
= (400 + 10h)g dh
p = (400h + 5h2)g
Therefore pressure at a point 8 m below is
p(h = 8) = (400 × 8 + 5 × 82) × 9.81
p(h = 8) = 34531 Pa
≃ 34.531 kPa
A dam is having a curved surface as shown in the figure. The height of the water retained by the dam is 20 m, density of water is 1000 kg/m3. Assuming g as 9.81 m/s2, the vertical force in kN acting on the dam per unit length is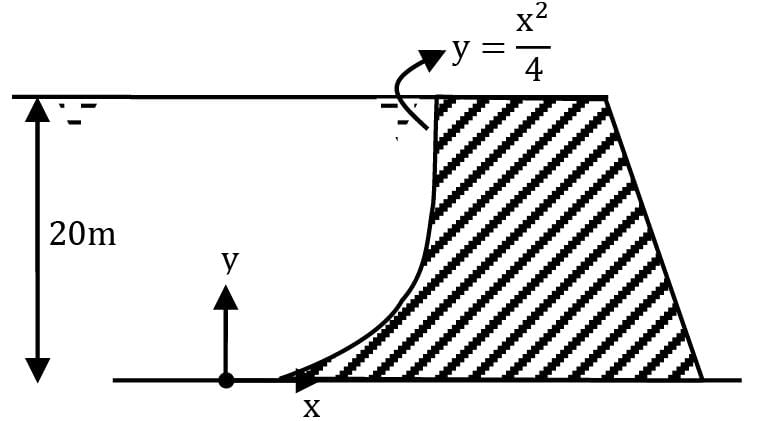 Correct answer is 'Range: 1169 to 1171'. Can you explain this answer?
Correct answer is 'Range: 1169 to 1171'. Can you explain this answer?
A dam is having a curved surface as shown in the figure. The height of the water retained by the dam is 20 m, density of water is 1000 kg/m3. Assuming g as 9.81 m/s2, the vertical force in kN acting on the dam per unit length is


|
Engineers Adda answered |
The vertical component of pressure force is equal to the weight of liquid above the curved surface. i.e. the volume between the curved surface and y-axis
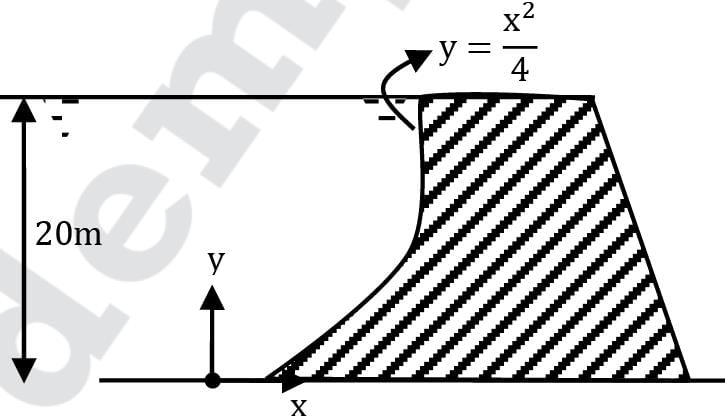
⇒ Fv = ρg ∫y=020 x dy × 1
⇒ Fv = 4 × 9810 / 3× 203/2
⇒ Fv = 1169.9 × 103 N Or 1169.9 kN
Calculate the pressure at a height of 6500m above the sea level if the atmospheric pressure is 10.145 N/cm2 and temperature is 25℃ assuming air is incompressible. Take density of air as 1.2 kg/m3. Neglect variation of g. - a)4.98 N/cm2
- b)2.49 N/cm2
- c)1.24 N/cm2
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Calculate the pressure at a height of 6500m above the sea level if the atmospheric pressure is 10.145 N/cm2 and temperature is 25℃ assuming air is incompressible. Take density of air as 1.2 kg/m3. Neglect variation of g.
a)
4.98 N/cm2
b)
2.49 N/cm2
c)
1.24 N/cm2
d)
None of the mentioned

|
Ashwin Gupta answered |
Explanation: Pressure= p – density of air*g*height
=101450-9.81*1.2*6500
= 2.49 N/cm2.
=101450-9.81*1.2*6500
= 2.49 N/cm2.
Which one of the following statements is true regarding pressure?- a)Pressure is a vector quantity
- b)Pressure is a vector quantity only when the area is infinitesimally small.
- c)Pressure is a scalar quantity only when the area is infinitesimally small
- d)Pressure is a scalar quantity
Correct answer is option 'D'. Can you explain this answer?
Which one of the following statements is true regarding pressure?
a)
Pressure is a vector quantity
b)
Pressure is a vector quantity only when the area is infinitesimally small.
c)
Pressure is a scalar quantity only when the area is infinitesimally small
d)
Pressure is a scalar quantity

|
Megha Choudhury answered |
Explanation:Pressure is defined as the force per unit area acting normal to a surface. Both force and area are vectors. but the division of one by the other leads to a scalar quantity.
The barometric pressure at sea level is 760 mm of Mercury while that on a mountain top is 715 mm. If the density of air is assumed constant at 1.2 kg/m3 , what is the elevation of the mountain top? - a)510 m
- b)1020 m
- c)255 m
- d)128 m
Correct answer is option 'A'. Can you explain this answer?
The barometric pressure at sea level is 760 mm of Mercury while that on a mountain top is 715 mm. If the density of air is assumed constant at 1.2 kg/m3 , what is the elevation of the mountain top?
a)
510 m
b)
1020 m
c)
255 m
d)
128 m

|
Ashwin Gupta answered |
Explanation: Gauge pressure at any height h = pressure at sea level – pressure at that height
h=(9.81*13600*0.76)-9.81*13600*0.715)/1.2*9.81
=510 m.
h=(9.81*13600*0.76)-9.81*13600*0.715)/1.2*9.81
=510 m.
Which device is popularly used for measuring difference of low pressure?- a)Inverted U-tube Differential Manometer
- b)U-tube Differential Manometer
- c)Inclined Single column manometer
- d)Vertical Single column manometer
Correct answer is option 'A'. Can you explain this answer?
Which device is popularly used for measuring difference of low pressure?
a)
Inverted U-tube Differential Manometer
b)
U-tube Differential Manometer
c)
Inclined Single column manometer
d)
Vertical Single column manometer

|
Rounak Saini answered |
Explanation: Inverted U-tube Differential Manometer has lighter manometric fluid, Hence it is used for measuring the low pressure difference.
A tank containing water upto a depth of 650 mm is stationary. Find the force exerted by fluid of specific gravity .55 on the side of tank,width of tank is 1.5m - a)1709.9 N
- b)3419.4N
- c)6838.8 N
- d)1367.75 N
Correct answer is option 'A'. Can you explain this answer?
A tank containing water upto a depth of 650 mm is stationary. Find the force exerted by fluid of specific gravity .55 on the side of tank,width of tank is 1.5m
a)
1709.9 N
b)
3419.4N
c)
6838.8 N
d)
1367.75 N

|
Kirti Sharma answered |
To find the force exerted by the fluid on the side of the tank, we can use the concept of hydrostatic pressure.
Hydrostatic pressure is the pressure exerted by a fluid at rest due to the force of gravity acting on the fluid column above. It can be calculated using the formula:
Pressure = density × gravity × height
In this case, the height of the fluid column is given as 650 mm or 0.65 m. The specific gravity of the fluid is given as 0.55, which means it is 0.55 times as dense as water.
Let's calculate the force exerted by the fluid on the side of the tank using the given data:
1. Convert the height of the fluid column from millimeters to meters:
Height = 650 mm = 0.65 m
2. Calculate the density of the fluid:
Density = specific gravity × density of water
Density = 0.55 × 1000 kg/m³ (density of water)
Density = 550 kg/m³
3. Calculate the force exerted by the fluid:
Force = pressure × area
The area of the side of the tank can be calculated using the width of the tank, which is given as 1.5 m. Since the force is exerted uniformly on the entire side of the tank, we can take the area as the product of the width and the height of the tank.
Area = width × height
Area = 1.5 m × 0.65 m
Area = 0.975 m²
Now, we can calculate the force:
Force = pressure × area
Force = density × gravity × height × area
Force = 550 kg/m³ × 9.8 m/s² × 0.65 m × 0.975 m²
Force ≈ 1709.9 N
Therefore, the force exerted by the fluid of specific gravity 0.55 on the side of the tank is approximately 1709.9 N.
Hydrostatic pressure is the pressure exerted by a fluid at rest due to the force of gravity acting on the fluid column above. It can be calculated using the formula:
Pressure = density × gravity × height
In this case, the height of the fluid column is given as 650 mm or 0.65 m. The specific gravity of the fluid is given as 0.55, which means it is 0.55 times as dense as water.
Let's calculate the force exerted by the fluid on the side of the tank using the given data:
1. Convert the height of the fluid column from millimeters to meters:
Height = 650 mm = 0.65 m
2. Calculate the density of the fluid:
Density = specific gravity × density of water
Density = 0.55 × 1000 kg/m³ (density of water)
Density = 550 kg/m³
3. Calculate the force exerted by the fluid:
Force = pressure × area
The area of the side of the tank can be calculated using the width of the tank, which is given as 1.5 m. Since the force is exerted uniformly on the entire side of the tank, we can take the area as the product of the width and the height of the tank.
Area = width × height
Area = 1.5 m × 0.65 m
Area = 0.975 m²
Now, we can calculate the force:
Force = pressure × area
Force = density × gravity × height × area
Force = 550 kg/m³ × 9.8 m/s² × 0.65 m × 0.975 m²
Force ≈ 1709.9 N
Therefore, the force exerted by the fluid of specific gravity 0.55 on the side of the tank is approximately 1709.9 N.
A circular plate 5.0 m diameter is immersed in such a way that its greatest and least depth below the free surface are 3 m and 1 m respectively. determine the position of the centre of pressure.- a)2.5 m
- b)5 m
- c)4.5 m
- d)6 m
Correct answer is option 'A'. Can you explain this answer?
A circular plate 5.0 m diameter is immersed in such a way that its greatest and least depth below the free surface are 3 m and 1 m respectively. determine the position of the centre of pressure.
a)
2.5 m
b)
5 m
c)
4.5 m
d)
6 m

|
Navya Saha answered |
Explanation: centre of pressure, ŷ=I*sin²θ/Aĥ + ĥ
…….ĥ=(y+dsinθ)
=3.142*2.54*sin²23.58/3.142*2.52*(1+2.5sin23.58)+*(1+2.5sin23.58)
=2.5 m.
…….ĥ=(y+dsinθ)
=3.142*2.54*sin²23.58/3.142*2.52*(1+2.5sin23.58)+*(1+2.5sin23.58)
=2.5 m.
Which of the following is NOT a characteristic of the liquid used in a manometer?- a)The liquid should stick on the walls
- b)High viscosity
- c)Low surface tension
- d)It should be immiscible
Correct answer is option 'B'. Can you explain this answer?
Which of the following is NOT a characteristic of the liquid used in a manometer?
a)
The liquid should stick on the walls
b)
High viscosity
c)
Low surface tension
d)
It should be immiscible
|
|
Sanvi Kapoor answered |
- For amplifying the deflection in a liquid column manometer, liquids with greater density could be used or one of the limbs of the manometer may be inclined.
- Commonly used manometric liquids are mercury, water, or alcohol.
- Some of the important and desirable properties of the manometric liquids are:
- High chemical stability
- Low viscosity
- Low capillary constant
- Low coefficient of thermal expansion
- Low volatility
- Low vapour pressure
- Low surface tension
- Sticky to wall
- Immiscible
What type of reservoir is used in a single column manometer?- a)Small
- b)Large
- c)Extremely small
- d)Size is irrelevant here
Correct answer is option 'B'. Can you explain this answer?
What type of reservoir is used in a single column manometer?
a)
Small
b)
Large
c)
Extremely small
d)
Size is irrelevant here

|
Subhankar Khanna answered |
The correct answer for the type of reservoir used in a single column manometer is option 'B' - Large.
A manometer is a device used to measure pressure differences between two points in a fluid. It consists of a U-shaped tube partially filled with a liquid, and the pressure difference is determined by the height difference of the liquid columns in the two arms of the tube.
In the case of a single column manometer, there is only one liquid column connected to the system being measured. This means that one end of the manometer is open to the atmosphere, while the other end is connected to the system. The height difference of the liquid column in the manometer indicates the pressure difference between the system and the atmosphere.
To ensure accurate readings, it is important to have a large reservoir connected to the system being measured. This reservoir acts as a buffer, ensuring a constant and steady flow of fluid into the manometer. It helps to minimize any fluctuations in pressure caused by variations in the system.
Having a large reservoir also helps to minimize the effect of any small changes in the fluid level in the manometer. If the reservoir is small, even a slight change in the fluid level can result in significant pressure differences, leading to inaccurate readings.
In contrast, a large reservoir provides a greater volume of fluid, allowing for a more stable and consistent pressure measurement. This reduces the chances of errors and provides reliable readings.
Additionally, a large reservoir also allows for a longer response time, which is beneficial when measuring fluctuating pressures or when dealing with systems that have dynamic pressure changes.
Therefore, it is crucial to use a large reservoir in a single column manometer to ensure accurate and reliable pressure measurements.
A manometer is a device used to measure pressure differences between two points in a fluid. It consists of a U-shaped tube partially filled with a liquid, and the pressure difference is determined by the height difference of the liquid columns in the two arms of the tube.
In the case of a single column manometer, there is only one liquid column connected to the system being measured. This means that one end of the manometer is open to the atmosphere, while the other end is connected to the system. The height difference of the liquid column in the manometer indicates the pressure difference between the system and the atmosphere.
To ensure accurate readings, it is important to have a large reservoir connected to the system being measured. This reservoir acts as a buffer, ensuring a constant and steady flow of fluid into the manometer. It helps to minimize any fluctuations in pressure caused by variations in the system.
Having a large reservoir also helps to minimize the effect of any small changes in the fluid level in the manometer. If the reservoir is small, even a slight change in the fluid level can result in significant pressure differences, leading to inaccurate readings.
In contrast, a large reservoir provides a greater volume of fluid, allowing for a more stable and consistent pressure measurement. This reduces the chances of errors and provides reliable readings.
Additionally, a large reservoir also allows for a longer response time, which is beneficial when measuring fluctuating pressures or when dealing with systems that have dynamic pressure changes.
Therefore, it is crucial to use a large reservoir in a single column manometer to ensure accurate and reliable pressure measurements.
In a stationary fluid, how does the local pressure of the fluid vary?- a)With depth only
- b)In the horizontal direction only
- c)Both with depth and along horizontal direction
- d)Neither with depth nor along horizontal direction
Correct answer is option 'A'. Can you explain this answer?
In a stationary fluid, how does the local pressure of the fluid vary?
a)
With depth only
b)
In the horizontal direction only
c)
Both with depth and along horizontal direction
d)
Neither with depth nor along horizontal direction

|
Kavya Mehta answered |
Pressure variation in a stationary fluid:
Pressure in a fluid at rest, like water in a container, depends only on the depth of the fluid. This is due to the gravitational force acting on the fluid.
Explanation:
Example:
Consider a container filled with water. If you go deeper into the water, you will experience an increase in pressure. This is why deep-sea divers wear special suits to handle the high pressure at greater depths.
Conclusion:
In a stationary fluid, such as water in a container, the local pressure varies only with depth and not along the horizontal direction. This is a fundamental principle in fluid mechanics and is crucial for various engineering applications.
Pressure in a fluid at rest, like water in a container, depends only on the depth of the fluid. This is due to the gravitational force acting on the fluid.
Explanation:
- With depth only: The pressure in a fluid increases with depth. This is because at greater depths, there is more fluid above exerting a greater force due to gravity. The pressure at any point in a fluid is directly proportional to the depth of the fluid above that point.
Example:
Consider a container filled with water. If you go deeper into the water, you will experience an increase in pressure. This is why deep-sea divers wear special suits to handle the high pressure at greater depths.
Conclusion:
In a stationary fluid, such as water in a container, the local pressure varies only with depth and not along the horizontal direction. This is a fundamental principle in fluid mechanics and is crucial for various engineering applications.
A circular opening, 6m diameter, in a vertical side of a tank is closed by a disc of 6m diameter which can rotate about a horizontal diameter. Calculate the force on the disc. The centre of circular opening is at the depth of 5 m.- a)1.38 MN
- b)2.76 MN
- c)5.54 MN
- d)7.85 MN
Correct answer is option 'A'. Can you explain this answer?
A circular opening, 6m diameter, in a vertical side of a tank is closed by a disc of 6m diameter which can rotate about a horizontal diameter. Calculate the force on the disc. The centre of circular opening is at the depth of 5 m.
a)
1.38 MN
b)
2.76 MN
c)
5.54 MN
d)
7.85 MN

|
Muskaan Sen answered |
Explanation: F=w*A*ŷ
=9.81*1000*3.142*32*5
=1.38 MN.
=9.81*1000*3.142*32*5
=1.38 MN.
All fluids in Figure below are at 20°C. If atmospheric pressure = 101.33 kPa and the bottom pressure is 242 kPa absolute, what is the specific gravity of fluid X?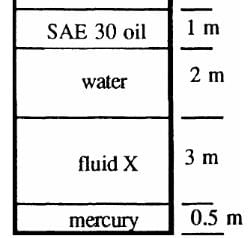
- a)1.44
- b)1.38
- c)1.29
- d)1.56
Correct answer is option 'D'. Can you explain this answer?
All fluids in Figure below are at 20°C. If atmospheric pressure = 101.33 kPa and the bottom pressure is 242 kPa absolute, what is the specific gravity of fluid X?

a)
1.44
b)
1.38
c)
1.29
d)
1.56

|
Rajdeep Gupta answered |
Explanation:Simply apply the hydrostatic equation from top to bottom:
Pbottom = Ptop + ∑ γ h
or: 242000 = 101330+ (8720)(1.0)+(9790)(2.0)+ γx(3.0)+ (133100)(0.5)
Solve for γx = 15273N/m2
or: SGx = 15273/9790 = 1.56
Pascal's law states that pressure at a point is equal in all directions, in a- a)static solid
- b)static fluid
- c)static gas
- d)moving fluid
Correct answer is option 'B'. Can you explain this answer?
Pascal's law states that pressure at a point is equal in all directions, in a
a)
static solid
b)
static fluid
c)
static gas
d)
moving fluid
|
|
Lavanya Menon answered |
Concept:
According to Blaise Pascal, a French scientist observed that the pressure in a fluid at rest is the same at all points if they are at the same height and it is termed Pascal’s Law.
According to Blaise Pascal, a French scientist observed that the pressure in a fluid at rest is the same at all points if they are at the same height and it is termed Pascal’s Law.
Proof of Pascal's law. ABC-DEF is an element of the interior of a fluid at rest. This element is in the form of a right-angled prism. The element is small so that the effect of gravity can be ignored, but it has been enlarged for the sake of clarity
i.e., the pressure exerted by the fluid on an object at a certain height will be the same in all direction and hence it can be expressed as
From the above fig. we can see that the force against area within a fluid at rest will always experience pressure perpendicular to their surface area, and the object will experience equal pressure throughout the surface.
And there are a number of devices, such as hydraulic lift and hydraulic brakes, are based on Pascal’s law, these devices used fluids for transmitting pressure.
A pipe line which is 6 m in diameter contains a gate valve. The pressure at the centre of the pipe is 25 N/cm2. If the pipe is filled with specific gravity 0.8, find the force exerted by the oil upon the gate.- a)7.06 MN
- b)14.12 MN
- c)3.53 MN
- d)28.24 MN
Correct answer is option 'A'. Can you explain this answer?
A pipe line which is 6 m in diameter contains a gate valve. The pressure at the centre of the pipe is 25 N/cm2. If the pipe is filled with specific gravity 0.8, find the force exerted by the oil upon the gate.
a)
7.06 MN
b)
14.12 MN
c)
3.53 MN
d)
28.24 MN

|
Aarav Chauhan answered |
Explanation: ĥ=p/ρg
=250000/9.81*800
=31.855 m
F=wAĥ
=9.81*800*9*π*31.855
=7.06 MN.
=250000/9.81*800
=31.855 m
F=wAĥ
=9.81*800*9*π*31.855
=7.06 MN.
What is the viscosity of water at 30oC?- a)80.1
- b)0 .801
- c)801
- d)0.081
Correct answer is option 'B'. Can you explain this answer?
What is the viscosity of water at 30oC?
a)
80.1
b)
0 .801
c)
801
d)
0.081
|
|
Sanya Agarwal answered |
A graph is plotted with temperature in the x-axis and dynamic viscosity in the y-axis. With the increase in pressure the viscosity decreases. It corresponds to an informal concept of thickness.
Chapter doubts & questions for Fluid Pressure & Its Measurement - 6 Months Preparation for GATE Mechanical 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Fluid Pressure & Its Measurement - 6 Months Preparation for GATE Mechanical in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
6 Months Preparation for GATE Mechanical
499 videos|1037 docs|710 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily