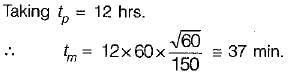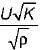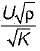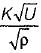All Exams >
Mechanical Engineering >
6 Months Preparation for GATE Mechanical >
All Questions
All questions of Dimensional Analysis for Mechanical Engineering Exam
A model of reservoir is emptied in 10 minutes. If the model scale is 1:25, the time taken by the prototype to empty itself, would be- a)250 min
- b)50 min
- c)6250 min
- d)2 min
Correct answer is option 'B'. Can you explain this answer?
A model of reservoir is emptied in 10 minutes. If the model scale is 1:25, the time taken by the prototype to empty itself, would be
a)
250 min
b)
50 min
c)
6250 min
d)
2 min

|
Subham Unni answered |
Given:
Time taken by model to empty = 10 min
Model scale = 1:25
To find:
Time taken by prototype to empty
Solution:
Let's assume the volume of the reservoir in the model as Vm and the volume of the reservoir in the prototype as Vp.
We know that the volume of the model is 1/25 times the volume of the prototype.
Vm/Vp = 1/25
=> Vp = 25Vm
Now, let's assume the rate at which the model empties as Rm and the rate at which the prototype empties as Rp.
We know that the rate of the model is same as the rate of the prototype.
Rm = Rp
We also know that the time taken by the model to empty is 10 minutes.
Therefore, the volume of the model emptied in 1 minute is Vm/10.
Volume emptied in 1 minute by prototype = Vp/?
=> Vp/? = Vm/10
=> 25Vm/? = Vm/10
=> ? = 250 minutes
Therefore, the time taken by the prototype to empty itself is 250 minutes or 50 minutes (since 1 minute in the model corresponds to 25 minutes in the prototype).
Answer: Option B) 50 min
Time taken by model to empty = 10 min
Model scale = 1:25
To find:
Time taken by prototype to empty
Solution:
Let's assume the volume of the reservoir in the model as Vm and the volume of the reservoir in the prototype as Vp.
We know that the volume of the model is 1/25 times the volume of the prototype.
Vm/Vp = 1/25
=> Vp = 25Vm
Now, let's assume the rate at which the model empties as Rm and the rate at which the prototype empties as Rp.
We know that the rate of the model is same as the rate of the prototype.
Rm = Rp
We also know that the time taken by the model to empty is 10 minutes.
Therefore, the volume of the model emptied in 1 minute is Vm/10.
Volume emptied in 1 minute by prototype = Vp/?
=> Vp/? = Vm/10
=> 25Vm/? = Vm/10
=> ? = 250 minutes
Therefore, the time taken by the prototype to empty itself is 250 minutes or 50 minutes (since 1 minute in the model corresponds to 25 minutes in the prototype).
Answer: Option B) 50 min
A 1: 30 scale model of a submarine is to be tested in a wind tunnel for its drag when it is operating at 15 km/h in ocean. The kinematic viscosity of air is 1.51 x 10-5 m2/s and for water 1.02 x 10-6 m2/s. What is the velocity of air in wind tunnel that should be maintained for kinematic similarity?- a)1500 m/s
- b)2000 m/s
- c)1850.5 m/s
- d)2500.5 m/s
Correct answer is option 'C'. Can you explain this answer?
A 1: 30 scale model of a submarine is to be tested in a wind tunnel for its drag when it is operating at 15 km/h in ocean. The kinematic viscosity of air is 1.51 x 10-5 m2/s and for water 1.02 x 10-6 m2/s. What is the velocity of air in wind tunnel that should be maintained for kinematic similarity?
a)
1500 m/s
b)
2000 m/s
c)
1850.5 m/s
d)
2500.5 m/s

|
Nilanjan Rane answered |
Given data:
Scale of the model: 1:30
Velocity of the submarine in water: 15 km/h
Kinematic viscosity of air: 1.51 x 10-5 m2/s
Kinematic viscosity of water: 1.02 x 10-6 m2/s
To achieve kinematic similarity between the model and the actual submarine, the velocities in the wind tunnel and in the ocean should be related by the equation:
(V_air_tunnel / V_water) = √(ν_air_tunnel / ν_water)
Where:
V_air_tunnel is the velocity of air in the wind tunnel
V_water is the velocity of water in the ocean
ν_air_tunnel is the kinematic viscosity of air in the wind tunnel
ν_water is the kinematic viscosity of water in the ocean
Let's calculate the values:
Convert the velocity of the submarine in water:
15 km/h = (15 * 1000) / (60 * 60) m/s = 4.17 m/s
Substitute the values into the equation:
(V_air_tunnel / 4.17) = √(1.51 x 10-5 / 1.02 x 10-6)
Simplify the equation:
V_air_tunnel = 4.17 * √(1.51 x 10-5 / 1.02 x 10-6)
Calculate the result:
V_air_tunnel = 4.17 * √14.8
V_air_tunnel ≈ 4.17 * 3.847
V_air_tunnel ≈ 16.08 m/s
Therefore, the velocity of air in the wind tunnel that should be maintained for kinematic similarity is approximately 16.08 m/s, which is closest to option C: 1850.5 m/s.
Scale of the model: 1:30
Velocity of the submarine in water: 15 km/h
Kinematic viscosity of air: 1.51 x 10-5 m2/s
Kinematic viscosity of water: 1.02 x 10-6 m2/s
To achieve kinematic similarity between the model and the actual submarine, the velocities in the wind tunnel and in the ocean should be related by the equation:
(V_air_tunnel / V_water) = √(ν_air_tunnel / ν_water)
Where:
V_air_tunnel is the velocity of air in the wind tunnel
V_water is the velocity of water in the ocean
ν_air_tunnel is the kinematic viscosity of air in the wind tunnel
ν_water is the kinematic viscosity of water in the ocean
Let's calculate the values:
Convert the velocity of the submarine in water:
15 km/h = (15 * 1000) / (60 * 60) m/s = 4.17 m/s
Substitute the values into the equation:
(V_air_tunnel / 4.17) = √(1.51 x 10-5 / 1.02 x 10-6)
Simplify the equation:
V_air_tunnel = 4.17 * √(1.51 x 10-5 / 1.02 x 10-6)
Calculate the result:
V_air_tunnel = 4.17 * √14.8
V_air_tunnel ≈ 4.17 * 3.847
V_air_tunnel ≈ 16.08 m/s
Therefore, the velocity of air in the wind tunnel that should be maintained for kinematic similarity is approximately 16.08 m/s, which is closest to option C: 1850.5 m/s.
Which of the following could be a π-parameter of the function f(F, V, r, m, L) = 0 when V, r and L are taken as repeating variables?- a)
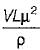
- b)
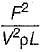
- c)
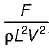
- d)

Correct answer is option 'C'. Can you explain this answer?
Which of the following could be a π-parameter of the function f(F, V, r, m, L) = 0 when V, r and L are taken as repeating variables?
a)
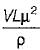
b)
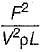
c)
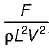
d)


|
Meghana Desai answered |
A π parameter is constant and has zero dimensional unit i.e. M°L°T°.
A ship’s model of scale 1 : 100 had a wave resistance of 1 kg at its design speed. The corresponding wave resistance in prototype will be- a)100kg
- b)10000kg
- c)1000000 kg
- d)1000 kg
Correct answer is option 'C'. Can you explain this answer?
A ship’s model of scale 1 : 100 had a wave resistance of 1 kg at its design speed. The corresponding wave resistance in prototype will be
a)
100kg
b)
10000kg
c)
1000000 kg
d)
1000 kg

|
Athira Pillai answered |
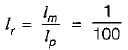
Froude model is applicable here because of influence of gravity force using froude model law,
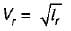
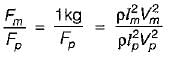
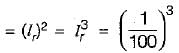
or, Fp = 1000000 kg
The distorted models, used in the hydraulic studies, are those which- a)have exaggeration of the vertical scale and horizontal scale
- b)are not geometrically similar to the prototypes
- c)have same vertical and horizontal scale as that of the prototypes
- d)have same Froude number as that for the prototypes
Correct answer is option 'B'. Can you explain this answer?
The distorted models, used in the hydraulic studies, are those which
a)
have exaggeration of the vertical scale and horizontal scale
b)
are not geometrically similar to the prototypes
c)
have same vertical and horizontal scale as that of the prototypes
d)
have same Froude number as that for the prototypes

|
Aditi Sarkar answered |
Distorted - model can have vertical scale exaggeration or slope exaggeration. Therefore they are not geometrically similar. It may have either geometrical distortion, or material distortion or distortion of hydraulic quantities or a combination of these.
Euler’s equation of motion- a)is applicable to any fluid
- b)considers only gravity and pressure forces acting on an inviscid fluid
- c)considers gravity and viscous forces acting on a real fluid
- d)considers only the pressure forces acting on a real fluid
Correct answer is option 'B'. Can you explain this answer?
Euler’s equation of motion
a)
is applicable to any fluid
b)
considers only gravity and pressure forces acting on an inviscid fluid
c)
considers gravity and viscous forces acting on a real fluid
d)
considers only the pressure forces acting on a real fluid

|
Simran Saha answered |
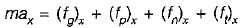
→ Reynold’s equation
fg → Due to gravity
fp → Due to pressure
fn → Due to viscosity
ft → Due to turbulence
max = (fg)x + (fp)x → Euler’s equation
(Neglected viscous force vand force due to turbulence)
The geometrical similarity between model and prototype is achieved by- a)using different model scales for horizontal and vertical dimension
- b)using the same model scale throughout
- c)having the same radius of curvature at identical places in model and prototype
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The geometrical similarity between model and prototype is achieved by
a)
using different model scales for horizontal and vertical dimension
b)
using the same model scale throughout
c)
having the same radius of curvature at identical places in model and prototype
d)
None of these

|
Prashanth Mehra answered |
Geometric similarity exists between the model and the prototype if the ratios of corresponding length dimensions in the model and the prototype are equal. Different model scales for horizontal and vertical dimension are used in a distorted model. Geometric similarity is achieved by using same model scale throughout.
A spillway of an irrigation project is to be studied by means of a model constructed to a scale of 1 : 9. The prototype discharge is 1000 m3/s. Neglecting the viscous and surface tension effects, the required flow rate for the model is- a)12.35 m3/s
- b)111.11 m3/s
- c)4.11 m3/s
- d)1.37 m3/s
Correct answer is option 'C'. Can you explain this answer?
A spillway of an irrigation project is to be studied by means of a model constructed to a scale of 1 : 9. The prototype discharge is 1000 m3/s. Neglecting the viscous and surface tension effects, the required flow rate for the model is
a)
12.35 m3/s
b)
111.11 m3/s
c)
4.11 m3/s
d)
1.37 m3/s

|
Alok Iyer answered |

Apart from inertia force, which of the following forces is most important in motion of submarines underwater?- a)viscous force
- b)gravity force
- c)compressive force
- d)surface tension force
Correct answer is option 'A'. Can you explain this answer?
Apart from inertia force, which of the following forces is most important in motion of submarines underwater?
a)
viscous force
b)
gravity force
c)
compressive force
d)
surface tension force

|
Gowri Singh answered |
The most important force in the motion of submarines underwater is viscous force. This force is caused by the friction between the water and the surface of the submarine as it moves through the water. The following points explain why viscous force is the most important force in the motion of submarines underwater:
• Resistance to motion: Viscous force is the force that opposes the motion of an object through a fluid. In the case of submarines, the friction between the water and the surface of the submarine creates a resistance to motion. This resistance is known as hydrodynamic drag. Viscous force is the dominant force that causes this drag.
• Effect on speed: The drag caused by viscous force reduces the speed of the submarine. This is why submarines are designed to be streamlined to reduce the drag caused by viscous force. The more streamlined a submarine is, the less viscous force it experiences and the faster it can move through the water.
• Effect on maneuverability: Viscous force can also affect the maneuverability of submarines. As the submarine changes direction, it experiences different amounts of drag on different parts of its surface. This can cause the submarine to rotate or pitch, which can affect its stability. Submarines are designed to have a balance between stability and maneuverability to ensure they can perform their missions effectively.
In conclusion, viscous force is the most important force in the motion of submarines underwater because it creates the resistance to motion that reduces speed and affects maneuverability. Understanding the effects of viscous force is essential for designing submarines that can perform effectively in their underwater environment.
• Resistance to motion: Viscous force is the force that opposes the motion of an object through a fluid. In the case of submarines, the friction between the water and the surface of the submarine creates a resistance to motion. This resistance is known as hydrodynamic drag. Viscous force is the dominant force that causes this drag.
• Effect on speed: The drag caused by viscous force reduces the speed of the submarine. This is why submarines are designed to be streamlined to reduce the drag caused by viscous force. The more streamlined a submarine is, the less viscous force it experiences and the faster it can move through the water.
• Effect on maneuverability: Viscous force can also affect the maneuverability of submarines. As the submarine changes direction, it experiences different amounts of drag on different parts of its surface. This can cause the submarine to rotate or pitch, which can affect its stability. Submarines are designed to have a balance between stability and maneuverability to ensure they can perform their missions effectively.
In conclusion, viscous force is the most important force in the motion of submarines underwater because it creates the resistance to motion that reduces speed and affects maneuverability. Understanding the effects of viscous force is essential for designing submarines that can perform effectively in their underwater environment.
An orifice is discharging under a head of 1.25 m of water. A Pitot tube kept at its centre line at the vena contracta indicates a heap of 1.20 m of water. The coefficient of velocity of the orifice is- a)0.99
- b)0.98
- c)0.965
- d)0.96
Correct answer is option 'B'. Can you explain this answer?
An orifice is discharging under a head of 1.25 m of water. A Pitot tube kept at its centre line at the vena contracta indicates a heap of 1.20 m of water. The coefficient of velocity of the orifice is
a)
0.99
b)
0.98
c)
0.965
d)
0.96

|
Niharika Yadav answered |
h0 be the head of Orifice
hp be the head of Pitot tube
Velocity of emergence of water from orifice can be given by =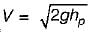
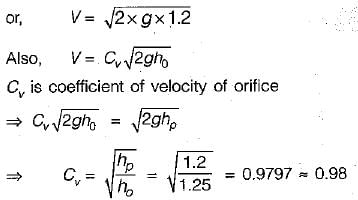
hp be the head of Pitot tube
Velocity of emergence of water from orifice can be given by =
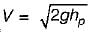
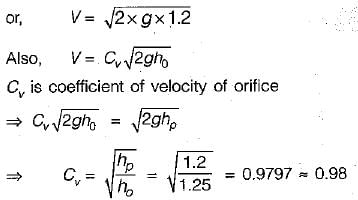
Assuming that the thrust T of a propeller depends on the diameter D, speed of advance V, angular velocity ω, dynamic viscosity μ and mass density ρ, which of the following ’non -dimensional parameters can be derived ‘by dimensional analysis?- a)1,2 and 3
- b)2, 3 and 4
- c)1,3 and 4
- d)1,2 and 4
Correct answer is option 'C'. Can you explain this answer?
Assuming that the thrust T of a propeller depends on the diameter D, speed of advance V, angular velocity ω, dynamic viscosity μ and mass density ρ, which of the following ’non -dimensional parameters can be derived ‘by dimensional analysis?
a)
1,2 and 3
b)
2, 3 and 4
c)
1,3 and 4
d)
1,2 and 4

|
Muskaan Sen answered |
Ω, and the density of the fluid ρ, we can write the equation for thrust as:
T = f(D, V, ω, ρ)
To determine the relationship between thrust and each of the variables, we need to consider the physical principles involved.
1. Diameter (D): The thrust generated by a propeller is directly proportional to the square of its diameter. This can be expressed as:
T ∝ D^2
2. Speed of advance (V): The thrust generated by a propeller is directly proportional to the cube of the speed of advance. This can be expressed as:
T ∝ V^3
3. Angular velocity (ω): The thrust generated by a propeller is directly proportional to the square of the angular velocity. This can be expressed as:
T ∝ ω^2
4. Density of the fluid (ρ): The thrust generated by a propeller is directly proportional to the density of the fluid. This can be expressed as:
T ∝ ρ
Combining these relationships, we can write the equation for thrust as:
T = k * D^2 * V^3 * ω^2 * ρ
where k is a constant that takes into account other factors such as efficiency, blade shape, and propeller design.
T = f(D, V, ω, ρ)
To determine the relationship between thrust and each of the variables, we need to consider the physical principles involved.
1. Diameter (D): The thrust generated by a propeller is directly proportional to the square of its diameter. This can be expressed as:
T ∝ D^2
2. Speed of advance (V): The thrust generated by a propeller is directly proportional to the cube of the speed of advance. This can be expressed as:
T ∝ V^3
3. Angular velocity (ω): The thrust generated by a propeller is directly proportional to the square of the angular velocity. This can be expressed as:
T ∝ ω^2
4. Density of the fluid (ρ): The thrust generated by a propeller is directly proportional to the density of the fluid. This can be expressed as:
T ∝ ρ
Combining these relationships, we can write the equation for thrust as:
T = k * D^2 * V^3 * ω^2 * ρ
where k is a constant that takes into account other factors such as efficiency, blade shape, and propeller design.
In model similarity, if gravitational and inertial forces are the only important forces, then what is the discharge ratio?
where Lr = ratio of length dimension.- a)Lr3/2
- b)Lr1/2
- c)Lr5/2
- d)Lr1/3
Correct answer is option 'C'. Can you explain this answer?
In model similarity, if gravitational and inertial forces are the only important forces, then what is the discharge ratio?
where Lr = ratio of length dimension.
where Lr = ratio of length dimension.
a)
Lr3/2
b)
Lr1/2
c)
Lr5/2
d)
Lr1/3

|
Ashwin Kulkarni answered |
If gravitational and inertial forces are the only important forces, then the Froude number must be the same in the model and prototype. Thus,
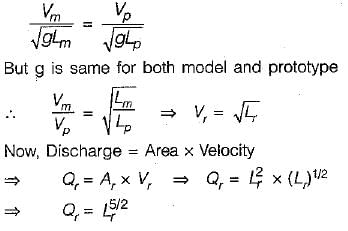
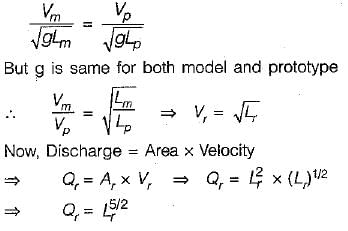
When Mach number is more than 6, the flow is called- a)subsonic flow
- b)sonic flow
- c)supersonic flow
- d)hypersonic flow
Correct answer is option 'D'. Can you explain this answer?
When Mach number is more than 6, the flow is called
a)
subsonic flow
b)
sonic flow
c)
supersonic flow
d)
hypersonic flow

|
Akanksha Mehta answered |

when the Mach number in flow region is slightly less to slightly greater than 1, flow is transonic flow.
Euler number or pressure coefficient may be represented as (notations have their usual meanings)- a)Δp/yH
- b)Δp/(pV2/2
- c)Δp/μV/L
- d)Δp/pLg
Correct answer is option 'B'. Can you explain this answer?
Euler number or pressure coefficient may be represented as (notations have their usual meanings)
a)
Δp/yH
b)
Δp/(pV2/2
c)
Δp/μV/L
d)
Δp/pLg

|
Bhavya Ahuja answered |
Euler number: Eu = ρvL/μ
where ρ is the density of the fluid, v is the velocity of the fluid, L is a characteristic length, and μ is the dynamic viscosity of the fluid.
b) Pressure coefficient: Cp = (p - p_∞)/(1/2ρv^2)
where p is the pressure at a point on the surface, p_∞ is the freestream pressure, ρ is the density of the fluid, and v is the velocity of the fluid.
where ρ is the density of the fluid, v is the velocity of the fluid, L is a characteristic length, and μ is the dynamic viscosity of the fluid.
b) Pressure coefficient: Cp = (p - p_∞)/(1/2ρv^2)
where p is the pressure at a point on the surface, p_∞ is the freestream pressure, ρ is the density of the fluid, and v is the velocity of the fluid.
Chapter doubts & questions for Dimensional Analysis - 6 Months Preparation for GATE Mechanical 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Dimensional Analysis - 6 Months Preparation for GATE Mechanical in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
6 Months Preparation for GATE Mechanical
499 videos|1037 docs|710 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup