All Exams >
MCAT >
MCAT Chemical and Physical Foundations >
All Questions
All questions of Force (PHY) for MCAT Exam
The centre of mass of a body is locateda)outside the systemb)inside or outside the systemc)inside the systemd)at the centre of systemCorrect answer is option 'B'. Can you explain this answer?
|
|
Suresh Iyer answered |
The centre of mass of a body can lie within or outside the body.
Example
(i) Centre of mass of a uniform rod lies at its geometrical centre which lies within the rod
(ii) Centre of mass of a uniform ring lies at its geometrical centre which lies outside the ring.
Example
(i) Centre of mass of a uniform rod lies at its geometrical centre which lies within the rod
(ii) Centre of mass of a uniform ring lies at its geometrical centre which lies outside the ring.
Can you explain the answer of this question below:Two blocks of the masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block. The velocity of centre of mass is
- A:
10 m/s
- B:
5 m/s
- C:
15 m/s
- D:
20 m/s
The answer is a.
Two blocks of the masses 10 kg and 4 kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse gives a velocity of 14 m/s to the heavier block. The velocity of centre of mass is
10 m/s
5 m/s
15 m/s
20 m/s

|
EduRev JEE answered |
Velocity of heavier block (v2) = 14m/s
Velocity of lighter block (v1) = 0m/s
Velocity of centre of mass,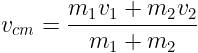
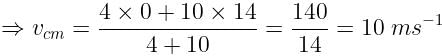
Velocity of lighter block (v1) = 0m/s
Velocity of centre of mass,
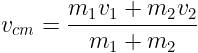
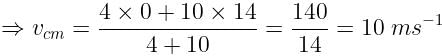
A mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin
- a)Is zero
- b)Remains constant
- c)Goes on increasing
- d)Goes on decreasing
Correct answer is option 'B'. Can you explain this answer?
A mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin
a)
Is zero
b)
Remains constant
c)
Goes on increasing
d)
Goes on decreasing
|
|
Krishna Iyer answered |
Angular momentum (L) is defined as the distance of the object from a rotation axis multiplied by the linear momentum
L = mv×y
L = mv×y
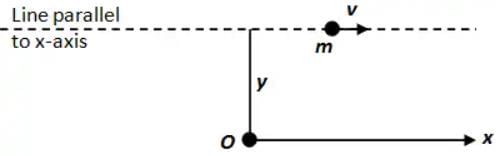
As the particle moves, m; v; and y, all remain unchanged at any point of time
⇒ L = constant
⇒ L = constant
There are two objects of masses 1 kg and 2 kg located at (1, 2) and (-1, 3) respectively. The coordinates of the centre of mass are- a)( 2, -1 )
- b)( 8/3 ,-1/3 )
- c)( -1/3 , 8/3 )
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
There are two objects of masses 1 kg and 2 kg located at (1, 2) and (-1, 3) respectively. The coordinates of the centre of mass are
a)
( 2, -1 )
b)
( 8/3 ,-1/3 )
c)
( -1/3 , 8/3 )
d)
none of these
|
|
Riya Banerjee answered |
Body A has mass of 1kg and location (1,2)
Body B has mass of 2kg and location (-1,3)
Body B has mass of 2kg and location (-1,3)
mcxc = m1x1 + m2x2
(1+2) xc = (1 * 1) + (2 * -1)
xc = -1/3
(1+2) xc = (1 * 1) + (2 * -1)
xc = -1/3
Similarly,
mcyc = m1y1 + m2y2
(1 + 2) yc = (1 * 2) + (2 * 3)
yc= 8/3
mcyc = m1y1 + m2y2
(1 + 2) yc = (1 * 2) + (2 * 3)
yc= 8/3
Hence, the coordinates of the center of mass are (-1/3, 8/3).
If a shell at rest explodes then the centre of mass of the fragments
- a)remains at rest
- b)Moves along a parabolic path
- c)Moves along a straight line
- d)moves along an elliptical path
Correct answer is option 'A'. Can you explain this answer?
If a shell at rest explodes then the centre of mass of the fragments
a)
remains at rest
b)
Moves along a parabolic path
c)
Moves along a straight line
d)
moves along an elliptical path
|
|
Gaurav Kumar answered |
As a shell explosion is not governed by any external force, we get that no external force acts upon the shell, and hence it remains at rest.
The motion of a potter’s wheel is an example of
- a)rolling motion
- b)rotatory motion
- c)translatory motion
- d)precessional motion
Correct answer is option 'B'. Can you explain this answer?
The motion of a potter’s wheel is an example of
a)
rolling motion
b)
rotatory motion
c)
translatory motion
d)
precessional motion
|
|
Anjali Iyer answered |
Potter’s wheel is an example of rotary motion. Rotary motion is that kind of motion in which body of the mass moves along a circular path about an axis which remains fixed.
The centre of mass of a system of particles does not depend on
- a)masses of the particles
- b)forces on the particles
- c)relative distances between the particles
- d)position of the particles
Correct answer is option 'B'. Can you explain this answer?
The centre of mass of a system of particles does not depend on
a)
masses of the particles
b)
forces on the particles
c)
relative distances between the particles
d)
position of the particles
|
|
Neha Joshi answered |
The resultant of all forces, on any system of particles, is zero. Therefore, their centre of mass does not depend upon the forces acting on the particles.
If a man of mass M jumps to the ground from height h and his centre of mass moves a distance x in the time taken by him to hit the ground, the average force acting on him is (assuming his retardation to be constant during his impact with the ground)- a)
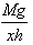
- b)
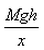
- c)
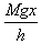
- d)
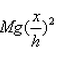
Correct answer is option 'B'. Can you explain this answer?
If a man of mass M jumps to the ground from height h and his centre of mass moves a distance x in the time taken by him to hit the ground, the average force acting on him is (assuming his retardation to be constant during his impact with the ground)
a)
b)
c)
d)
|
|
Neha Joshi answered |
As the center of mass moves through a distance x, the average force F acting on the man is calculated from :
Work done = Change in potential energy
⇒ Fx = Mgh
⇒ F =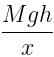
Work done = Change in potential energy
⇒ Fx = Mgh
⇒ F =
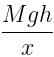
A block of mass 1kg is placed on the floor. The coefficient of static friction is 0.2. If a force of 1N is applied to the block, the force of friction is- a)0
- b)2 N
- c)1 N
- d)varies with the area of contact of the block
Correct answer is option 'C'. Can you explain this answer?
A block of mass 1kg is placed on the floor. The coefficient of static friction is 0.2. If a force of 1N is applied to the block, the force of friction is
a)
0
b)
2 N
c)
1 N
d)
varies with the area of contact of the block

|
Ayush Joshi answered |
The applied force is less than the maximum value of static friction which will be (0.2)(1kg)(10) = 2N. So the force of friction is equal to the applied force.
After the body starts moving, the friction involved with motion is- a)Static Friction
- b)Rolling Friction
- c)Sliding Friction
- d)Kinetic Friction
Correct answer is option 'D'. Can you explain this answer?
After the body starts moving, the friction involved with motion is
a)
Static Friction
b)
Rolling Friction
c)
Sliding Friction
d)
Kinetic Friction
|
|
Gaurav Kumar answered |
When the body is in rest it is under static friction but when it starts moving (neither rolling nor sliding), the static friction slowly chngs to kinetic friction as the coefficient of static friction start decreasing and that of kinetic friction starts increasing. In case it starts rolling motion then the friction is rolling friction & if it slides then sliding fiction.
When external forces acting on a body are zero, then its centre of mass- a)remains stationary
- b)moves with uniform velocity
- c)either remains stationary or moves with uniform velocity
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
When external forces acting on a body are zero, then its centre of mass
a)
remains stationary
b)
moves with uniform velocity
c)
either remains stationary or moves with uniform velocity
d)
none of these
|
|
Naina Sharma answered |
When force acting upon the body results zero, the resulting acceleration due to net force applied is also zero, and hence by the law of inertia the motion of the body either at rest or constant velocity wont change.
There are some passengers inside a stationary railway compartment. The centre of masses of the compartment itself(without the passengers) is C1, while the centre of mass of the compartment plus passengers’ system is C2. if the passengers moves about inside the compartment
- a)both C1 and C2 will move with respect to the ground
- b)neither C1 nor C2 will move with respect to the ground
- c)C1 will move but C2 will be stationary with respect to the ground
- d)C2 will move but C1 will be stationary with respect to the ground
Correct answer is option 'C'. Can you explain this answer?
There are some passengers inside a stationary railway compartment. The centre of masses of the compartment itself(without the passengers) is C1, while the centre of mass of the compartment plus passengers’ system is C2. if the passengers moves about inside the compartment
a)
both C1 and C2 will move with respect to the ground
b)
neither C1 nor C2 will move with respect to the ground
c)
C1 will move but C2 will be stationary with respect to the ground
d)
C2 will move but C1 will be stationary with respect to the ground
|
|
Lavanya Menon answered |
When net Fexternal=0, then the centre of mass of the system remains at rest.
Thus if the passenger move inside the compartment which donot require any external force, so the centre of mass of the "passenger + compartment" system must remain at rest and hence C2 will be fixed w.r.t ground.
Also due to the movement of the passenger, the position of centre of mass of the passengers only will change, thus C1 will have to move in such a way that C2 may remain fixed w.r.t ground.
A rigid body is one
- a)the sum of distances of all particles from the axis remains constant
- b)in which the distance between all pairs of particles remains fixed
- c)whose centre of mass follows a parabolic path
- d)that deforms and comes back to its original shape after getting deformed
Correct answer is option 'B'. Can you explain this answer?
A rigid body is one
a)
the sum of distances of all particles from the axis remains constant
b)
in which the distance between all pairs of particles remains fixed
c)
whose centre of mass follows a parabolic path
d)
that deforms and comes back to its original shape after getting deformed
|
|
Krishna Iyer answered |
A body is said to be a rigid body if the body remains in its original shape even under the influence of external force. We can also say that if distance between two points of the body does not change with time regardless of external forces exerted on it, then the body is said to be a rigid body.
When a wheel rolls on a level road, the direction of frictional force at the point of contact of wheel and ground is:
- a)along the tangent to the wheel
- b)forward direction
- c)along the centre of the wheel
- d)backward direction
Correct answer is option 'B'. Can you explain this answer?
When a wheel rolls on a level road, the direction of frictional force at the point of contact of wheel and ground is:
a)
along the tangent to the wheel
b)
forward direction
c)
along the centre of the wheel
d)
backward direction

|
Advait Ghoshal answered |
Frictional force is the opposing force which plays between two surfaces and it destroys the relative motion between them. Frictional force is a non-conservative force. The force produced by two surfaces that contact and slide against each other, that force is called the frictional force. These forces are affected by the nature of the surface and amount of force acting on them.
In case of a bicycle, the front wheel of the bicycle is connected to a rod passing through its centre. The force acting on the wheel about its central axis by the force coming from the rest of the bicycle is zero. Front wheel obtains linear velocity by pedalling but it cannot rotate it.
Wheel or ball can also be rolled by pushing on it. The frictional force prevents the wheel from sliding forward at the point of contact. Here, the frictional force prevents the wheel from sliding forward and it is in the opposite direction.
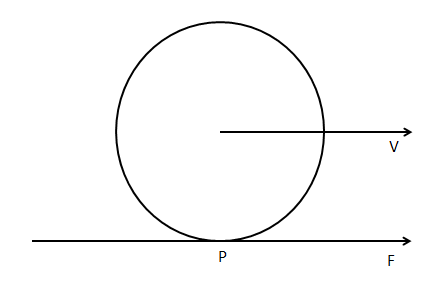
So, in the case of the wheel, the point P which is in contact with the ground tries to go backward due to rotation. Frictional force will oppose this motion. Hence it will move forward.
Hence the direction of frictional force at the point P of the wheel is in forward direction.
Note: Frictional force opposes the motion. Here static friction holds a wheel or a ball on the surface. Frictional force is equal and opposite in direction to the applied force parallel to the contacting surfaces. The resistance due to the rolling body on a surface is called rolling friction. Torque is a force that acts on a body that is undergoing rotation.
Impending motion of a body is opposed by- a)sliding friction
- b)rolling friction
- c)static friction
- d)kinetic friction
Correct answer is option 'C'. Can you explain this answer?
Impending motion of a body is opposed by
a)
sliding friction
b)
rolling friction
c)
static friction
d)
kinetic friction
|
|
Rajat Kapoor answered |
When the motion is not impending, b) Impending motion is the moment where the body is on the verge of slipping. Static friction force reaches the max value. For a given pair of mating surfaces, . c) Motion The body starts moving in the direction of the applied force.
If three balls of same radius are placed touching each other on a horizontal surface such that they will form an equilateral triangle, when their centers are joined. What will be the position of the centre of mass of the system?- a)At the point of intersection of the medians.
- b)At the line joining the centers of any two balls.
- c)At the centre of one of the ball.
- d)At the horizontal surface.
Correct answer is option 'A'. Can you explain this answer?
If three balls of same radius are placed touching each other on a horizontal surface such that they will form an equilateral triangle, when their centers are joined. What will be the position of the centre of mass of the system?
a)
At the point of intersection of the medians.
b)
At the line joining the centers of any two balls.
c)
At the centre of one of the ball.
d)
At the horizontal surface.
|
|
Neha Joshi answered |
The COM will be at the intersection point of the medians as that is the most symmetric point of this symmetric system.
When a shell was following a parabolic path in the air, it explodes somewhere in its flight. The centre of mass of fragments will continue to move in- a)any direction
- b)horizontal direction
- c)same parabolic path
- d)vertical direction
Correct answer is option 'C'. Can you explain this answer?
When a shell was following a parabolic path in the air, it explodes somewhere in its flight. The centre of mass of fragments will continue to move in
a)
any direction
b)
horizontal direction
c)
same parabolic path
d)
vertical direction
|
|
Riya Banerjee answered |
The internal forces have no effect on the trajectory of the center of mass, and the forces due to explosion are the internal forces. So the center of mass will follow the same parabolic path even after the explosion.
A block of mass 2kg rests on a plane inclined at an angle of 30o with the horizontal. The coefficient of friction between the block and the surface is 0.7. The frictional force acting on the block is
- a)9.8N
- b)0.7×9.8×3–√N
- c)12.5 N
- d)0.7×9.8N
Correct answer is option 'A'. Can you explain this answer?
A block of mass 2kg rests on a plane inclined at an angle of 30o with the horizontal. The coefficient of friction between the block and the surface is 0.7. The frictional force acting on the block is
a)
9.8N
b)
0.7×9.8×3–√N
c)
12.5 N
d)
0.7×9.8N
|
|
Rohan Singh answered |
Since the frictional force is self adjusting, the weight component acting down the inclined plane is mgsin?, which comes out to be 2 x 10 sin 30 = 10 N. So the frictional force balancing this downward force will also be 10 N acting up the plane.
Can you explain the answer of this question below:An isolated particle of mass m is moving in a horizontal plane (x,y) along the x axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. An instant later, the smaller fragments is at y = +15 cm. The larger fragment at this instant is at
- A:
y = +5 cm
- B:
y = +20 cm
- C:
y = -20 cm
- D:
y = -5 cm
The answer is d.
An isolated particle of mass m is moving in a horizontal plane (x,y) along the x axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. An instant later, the smaller fragments is at y = +15 cm. The larger fragment at this instant is at
y = +5 cm
y = +20 cm
y = -20 cm
y = -5 cm

|
Ambition Institute answered |
As the particle is exploded only due to its internal energy.
⇒ net external force during this process is 0 i.e. center mass will not change.
⇒ net external force during this process is 0 i.e. center mass will not change.
Let the particle while the explosion was above the origin of the coordinate system i.e. just before explosion xcm =0 and ycm =0
After the explosion, the Centre of mass will be at xcm =0 and ycm =0
Since smaller fragment has fallen on the y-axis.
Let positon of larger fragment be y.
Let positon of larger fragment be y.
m * ycm = (m/4 * 15) + (3m/4 * y)
⇒ (m/4 * 15) + (3m/4 * y) = 0
⇒ y = - 5 cm
⇒ (m/4 * 15) + (3m/4 * y) = 0
⇒ y = - 5 cm
A body rests on an inclined plane and the angle of inclination is varied till the body just begins to slide down. The coefficient of friction is 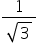 . What is the angle of inclination?
. What is the angle of inclination?- a)45o
- b)60o
- c)15o
- d)30o
Correct answer is option 'D'. Can you explain this answer?
A body rests on an inclined plane and the angle of inclination is varied till the body just begins to slide down. The coefficient of friction is 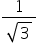 . What is the angle of inclination?
. What is the angle of inclination?
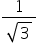 . What is the angle of inclination?
. What is the angle of inclination?a)
45o
b)
60o
c)
15o
d)
30o

|
Ambition Institute answered |
At the time when the block just starts to move, we get that net force acting upon it is 0, thus we get, f - mg.sin a = 0
Where f is friction force and a is angle of incline.
We also know that f = 1√3 x N
= 1√3 x mg.cos a
Thus we get 1√3 x mg.cos a = mg.sin a
Thus we get tan a = 1√3
And a = 30
Where f is friction force and a is angle of incline.
We also know that f = 1√3 x N
= 1√3 x mg.cos a
Thus we get 1√3 x mg.cos a = mg.sin a
Thus we get tan a = 1√3
And a = 30
A child sits stationary at one end of long trolley moving uniformly with speed v on a smooth horizontal floor. If the child gets up and runs about on the trolley in the forward direction with speed u. The centre of mass of the system (child + trolley) will move with speed- a)v
- b)zero
- c)u + v
- d)v/u
Correct answer is option 'A'. Can you explain this answer?
A child sits stationary at one end of long trolley moving uniformly with speed v on a smooth horizontal floor. If the child gets up and runs about on the trolley in the forward direction with speed u. The centre of mass of the system (child + trolley) will move with speed
a)
v
b)
zero
c)
u + v
d)
v/u
|
|
Preeti Iyer answered |
The child is running arbitrarily on a trolley moving with velocity v. However, the running of the child will produce no effect on the velocity of the centre of mass of the trolley. This is because the force due to the boy’s motion is purely internal. Internal forces produce no effect on the motion of the bodies on which they act. Since no external force is involved in the boy–trolley system, the boy’s motion will produce no change in the velocity of the centre of mass of the trolley.
If the net force acting on the system of particles is zero, then which of the following may vary
- a)moment of inertia
- b)Kinetic energy of the system
- c)velocity of centre of mass
- d)position of centre of mass
Correct answer is option 'D'. Can you explain this answer?
If the net force acting on the system of particles is zero, then which of the following may vary
a)
moment of inertia
b)
Kinetic energy of the system
c)
velocity of centre of mass
d)
position of centre of mass
|
|
Suresh Kumar answered |
Correct answer is B . because when a=0 then v=constant hence K.E. will be constant and position of com will vary
Three identical spheres each of radius R are placed such that their centres lie on a straight line. What is the location of their centre of mass from the centre of the first sphere?
- a)R
- b)2R
- c)3R
- d)4R
Correct answer is option 'B'. Can you explain this answer?
Three identical spheres each of radius R are placed such that their centres lie on a straight line. What is the location of their centre of mass from the centre of the first sphere?
a)
R
b)
2R
c)
3R
d)
4R
|
|
Geetika Shah answered |
- Distance between first and last sphere = R + 2R + R = 4R
- Since the spheres are identical and lie in a straight line, the centre of mass will lie exactly in the middle.
- Hence the centre of mass lies at a distance of 2R from the centre of the first sphere.
An object comprises of a uniform ring of radius R and its uniform chord AB (not necessarily made of the same material) as shown. Which of the following can not be the centre of mass of the object.
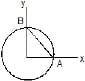
- a) (R/3, R/3)
- b) (R/3, R/2)
- c)(R/4, R/4)
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
An object comprises of a uniform ring of radius R and its uniform chord AB (not necessarily made of the same material) as shown. Which of the following can not be the centre of mass of the object.
a)
(R/3, R/3)
b)
(R/3, R/2)
c)
(R/4, R/4)
d)
None of these
|
|
Raghav Bansal answered |
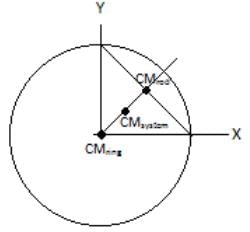
Since the points must have symmetric coordinates so B is the answer.
The sum of moments of masses of all the particles in a system about the centre of mass is always:- a)maximum
- b)infinite
- c)zero
- d)minimum
Correct answer is option 'C'. Can you explain this answer?
The sum of moments of masses of all the particles in a system about the centre of mass is always:
a)
maximum
b)
infinite
c)
zero
d)
minimum
|
|
Neha Sharma answered |
In physics, the center of mass of a distribution of mass in space is the unique point where the weighted relative position of the distributed mass sums to zero, or the point where if a force is applied it moves in the direction of the force without rotating. The distribution of mass is balanced around the center of mass and the average of the weighted position coordinates of the distributed mass defines its coordinates. Calculations in mechanics are often simplified when formulated with respect to the center of mass.
Every point in a rotating rigid body has the same __________at any instant of time.
- a)linear velocity
- b)angular velocity
- c)displacement
- d)linear momentum
Correct answer is option 'B'. Can you explain this answer?
Every point in a rotating rigid body has the same __________at any instant of time.
a)
linear velocity
b)
angular velocity
c)
displacement
d)
linear momentum
|
|
Preeti Iyer answered |
Every point in any rigid rotating object is rotating at the same angular velocity. However, there are a few cases where people have used the term "angular velocity" when they really meant tangential velocity, so you do have to be careful.
Which of the following statements best describes an object undergoing uniform circular motion?- a)The velocity and acceleration vectors are always tangential to each other.
- b)Objects in uniform circular motion tend to stay in uniform circular motion.
- c)The object moves with a constant velocity.
- d)The object would travel in a straight line if the acceleration vector goes to zero.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements best describes an object undergoing uniform circular motion?
a)
The velocity and acceleration vectors are always tangential to each other.
b)
Objects in uniform circular motion tend to stay in uniform circular motion.
c)
The object moves with a constant velocity.
d)
The object would travel in a straight line if the acceleration vector goes to zero.
|
|
Luna Howard answered |
Understanding Uniform Circular Motion
Uniform circular motion refers to the movement of an object along a circular path at a constant speed. Although the speed remains constant, the direction of the velocity vector continuously changes, leading to the presence of centripetal acceleration.
Why Option 'D' is Correct
- When an object is in uniform circular motion, it experiences a centripetal force, keeping it in a circular path.
- Acceleration Vector: This vector points towards the center of the circle, indicating that the object is continually changing direction.
- Straight-Line Movement: If the centripetal force (and thus the acceleration) were to disappear, the object would no longer have any force acting towards the center. According to Newton's first law of motion, an object in motion will continue in a straight line at constant speed if no net external force acts on it.
Other Options Explained
- Option A: Incorrect because, in uniform circular motion, the velocity vector is tangential to the circular path, while the acceleration vector is radial.
- Option B: Misleading; while an object in motion tends to stay in motion, it requires a force to maintain circular motion.
- Option C: Incorrect as "constant velocity" implies both constant speed and direction. In circular motion, the direction is continually changing.
Conclusion
In summary, option 'D' accurately reflects the behavior of an object in uniform circular motion. If the centripetal acceleration ceases, the object will move in a straight line, demonstrating the principle of inertia.
Uniform circular motion refers to the movement of an object along a circular path at a constant speed. Although the speed remains constant, the direction of the velocity vector continuously changes, leading to the presence of centripetal acceleration.
Why Option 'D' is Correct
- When an object is in uniform circular motion, it experiences a centripetal force, keeping it in a circular path.
- Acceleration Vector: This vector points towards the center of the circle, indicating that the object is continually changing direction.
- Straight-Line Movement: If the centripetal force (and thus the acceleration) were to disappear, the object would no longer have any force acting towards the center. According to Newton's first law of motion, an object in motion will continue in a straight line at constant speed if no net external force acts on it.
Other Options Explained
- Option A: Incorrect because, in uniform circular motion, the velocity vector is tangential to the circular path, while the acceleration vector is radial.
- Option B: Misleading; while an object in motion tends to stay in motion, it requires a force to maintain circular motion.
- Option C: Incorrect as "constant velocity" implies both constant speed and direction. In circular motion, the direction is continually changing.
Conclusion
In summary, option 'D' accurately reflects the behavior of an object in uniform circular motion. If the centripetal acceleration ceases, the object will move in a straight line, demonstrating the principle of inertia.
A scientist with mass m is sitting on one end of a lifeboat of uniform density with mass 3m3, m. When he spots a rescue chopper in the distance, he walks a distance of L to the other side of the lifeboat to wave for help. Which of the following statements best characterizes the motion of the lifeboat?- a)The lifeboat shifts in the same direction as the scientist’s motion with constant velocity.
- b)The lifeboat shifts by L/4 in the opposite direction of the scientist’s motion.
- c)The lifeboat does not shift forward or backward as a result of the scientist’s motion.
- d)The lifeboat shifts by the same distance traversed, but in the opposite direction of his motion.
Correct answer is option 'B'. Can you explain this answer?
A scientist with mass m is sitting on one end of a lifeboat of uniform density with mass 3m3, m. When he spots a rescue chopper in the distance, he walks a distance of L to the other side of the lifeboat to wave for help. Which of the following statements best characterizes the motion of the lifeboat?
a)
The lifeboat shifts in the same direction as the scientist’s motion with constant velocity.
b)
The lifeboat shifts by L/4 in the opposite direction of the scientist’s motion.
c)
The lifeboat does not shift forward or backward as a result of the scientist’s motion.
d)
The lifeboat shifts by the same distance traversed, but in the opposite direction of his motion.

|
Orion Classes answered |
The formula for center of mass is reminiscent of the equation for conservation of momentum for totally inelastic collisions, except that x replaces v.


Find the center of mass for his first position:
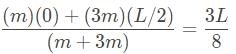
Find the center of mass for his second position. We assume the boat has shifted a distance x’ in the direction opposite the motion of the scientist. If we are wrong then we will get a negative value for x’.
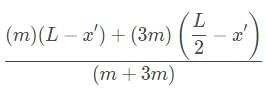
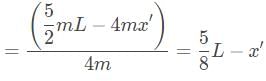
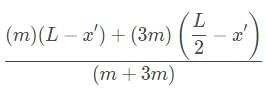
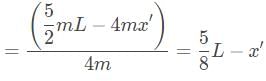
The boat starts in equilibrium, and will remain in equilibrium throughout the walk, so the center of mass remains stationary. Therefore we can set the expressions equal to one another to solve for x’:


The correct answer is that the center of mass shifts by L/4 in the opposite direction of the scientist’s motion.
The general motion of a rigid body consists of
- a)translational motion only
- b)rotational motion only
- c)both, translational and rotational motion
- d)does not include translational and rotational motions
Correct answer is option 'C'. Can you explain this answer?
The general motion of a rigid body consists of
a)
translational motion only
b)
rotational motion only
c)
both, translational and rotational motion
d)
does not include translational and rotational motions
|
|
Arun Khanna answered |
The general motion of a rigid body consists of both, translational and rotational motion. This is much obvious as it is seen all around us.
Which of the following force pairs represents an action-reaction pair?- a)Downward force of gravity on a falling object and upward force of air resistance at terminal velocity
- b)Weight of the book and normal force of the table
- c)Component of gravity along the plane of the incline on the block and static frictional force up along the plane
- d)Force of the horse on the cart and force of the cart on the horse
Correct answer is option 'D'. Can you explain this answer?
Which of the following force pairs represents an action-reaction pair?
a)
Downward force of gravity on a falling object and upward force of air resistance at terminal velocity
b)
Weight of the book and normal force of the table
c)
Component of gravity along the plane of the incline on the block and static frictional force up along the plane
d)
Force of the horse on the cart and force of the cart on the horse

|
Orion Classes answered |
- An action-reaction pair must consist of forces that are of the same type (field or contact) and that act on different objects.
- Weight is a field force, and normal force is a contact force, so they are not of the same type and act on the same object, i.e. book.
- At terminal velocity, the force of gravity equals the force of air resistance, but they are not the same type and act on the same object, i.e. falling object.
- Gravity along the plane of the incline and the static frictional force are equal, but they are not the same type and act on the same object, i.e. block.
- The only action-reaction pair is the force of the horse on the cart and force of the cart on the horse.
For an object with the centre of mass at the origin, the x-coordinates of particles of the object _____.
- a)maybe all positive.
- b)maybe all negative.
- c)maybe all non-negative.
- d)cannot be predicted.
Correct answer is option 'C'. Can you explain this answer?
For an object with the centre of mass at the origin, the x-coordinates of particles of the object _____.
a)
maybe all positive.
b)
maybe all negative.
c)
maybe all non-negative.
d)
cannot be predicted.
|
|
Tejas Verma answered |
- For an object to have the x-coordinate of its centre of mass, there should be particles on both the negative and positive coordinates of the plane for the sum to be zero.
- However, for 1-dimensional particles that all lie on the y-axis symmetric about the x-axis, the x-coordinate is zero – which is neither positive nor negative, i.e., non-negative.
Masses 1 kg, 1.5 kg, 2 kg, and “M” kg are situated at (2,1,1), (1,2,1), (2,-2,1) and (-1,4,3). What is the value of “M” if their centre of mass is at (1,1,3/2)?- a)1 kg
- b)1.5 kg
- c)2 kg
- d)2.5 kg
Correct answer is option 'B'. Can you explain this answer?
Masses 1 kg, 1.5 kg, 2 kg, and “M” kg are situated at (2,1,1), (1,2,1), (2,-2,1) and (-1,4,3). What is the value of “M” if their centre of mass is at (1,1,3/2)?
a)
1 kg
b)
1.5 kg
c)
2 kg
d)
2.5 kg
|
|
Tejas Verma answered |
Sum of masses = 1 + 1.5 + 2 + M = 4.5 + M
x-coordinate;
(1*2 + 1.5*1 + 2*2 – M)/(4.5 + M) = 1
4.5 + M = 7.5 – M
2M = 3
M = 1.5 kg.
x-coordinate;
(1*2 + 1.5*1 + 2*2 – M)/(4.5 + M) = 1
4.5 + M = 7.5 – M
2M = 3
M = 1.5 kg.
For which of the following does the centre of mass lie outside the body?- a)Pen
- b)Dice
- c)Rectangular tile
- d)Bangle
Correct answer is option 'D'. Can you explain this answer?
For which of the following does the centre of mass lie outside the body?
a)
Pen
b)
Dice
c)
Rectangular tile
d)
Bangle
|
|
Varun Kapoor answered |
- The centre of mass of a bangle lies at its geometric centre which does not lie on or in the object.
- Hence the centre of mass of a bangle lies outside the body.
Which of the following statements describes what must be true in the context of Newton’s First Law?- a)The tendency for drivers to keep moving linearly while the car makes a sharp turn on the road is an example of the concept of inertia.
- b)An object with zero acceleration and an object traveling at a constant acceleration are considered similar states.
- c)Mass is a measure of an object’s ability to resist motion or movement of any kind.
- d)The object is difficult to bring to a complete stop due to its high initial speed.
Correct answer is option 'A'. Can you explain this answer?
Which of the following statements describes what must be true in the context of Newton’s First Law?
a)
The tendency for drivers to keep moving linearly while the car makes a sharp turn on the road is an example of the concept of inertia.
b)
An object with zero acceleration and an object traveling at a constant acceleration are considered similar states.
c)
Mass is a measure of an object’s ability to resist motion or movement of any kind.
d)
The object is difficult to bring to a complete stop due to its high initial speed.
|
|
Daniel Lee answered |
Explanation:
Inertia and Newton's First Law:
- Newton's First Law states that an object will remain at rest or in uniform motion in a straight line unless acted upon by an external force. This is also known as the law of inertia.
- In the context of a car making a sharp turn, the tendency for drivers to keep moving linearly is an example of inertia. The passengers in the car will continue moving in a straight line due to their inertia, even though the car is turning.
Therefore, option 'A' is the correct statement that describes what must be true in the context of Newton's First Law.
Inertia and Newton's First Law:
- Newton's First Law states that an object will remain at rest or in uniform motion in a straight line unless acted upon by an external force. This is also known as the law of inertia.
- In the context of a car making a sharp turn, the tendency for drivers to keep moving linearly is an example of inertia. The passengers in the car will continue moving in a straight line due to their inertia, even though the car is turning.
Therefore, option 'A' is the correct statement that describes what must be true in the context of Newton's First Law.
The centre of masses of two particles with masses 2 kg and 1 kg located at (1,0,1) and (2,2,0) is located at:- a)4/3, 2/3, 2/3
- b)2/3, 4/3, 2/3
- c)2/3, 2/3, 4/3
- d)1/3, 2/3, 2/3
Correct answer is option 'A'. Can you explain this answer?
The centre of masses of two particles with masses 2 kg and 1 kg located at (1,0,1) and (2,2,0) is located at:
a)
4/3, 2/3, 2/3
b)
2/3, 4/3, 2/3
c)
2/3, 2/3, 4/3
d)
1/3, 2/3, 2/3
|
|
Tejas Verma answered |
Sum of masses = 2 + 1 = 3
x-coordinate;
(2*1 + 1*2)/3 = 4/3
y-coordinate;
(2*0 + 1*2)/3 = 2/3
z-coordinate;
(2*1 + 1*0)/3 = 2/3.
x-coordinate;
(2*1 + 1*2)/3 = 4/3
y-coordinate;
(2*0 + 1*2)/3 = 2/3
z-coordinate;
(2*1 + 1*0)/3 = 2/3.
A body has its centre of mass at the origin. The x-coordinates of the particles- a) May be all positive
- b) May be all negative
- c)May be all non-negative
- d)May be positive for some cases and negative in other cases
Correct answer is option 'C,D'. Can you explain this answer?
A body has its centre of mass at the origin. The x-coordinates of the particles
a)
May be all positive
b)
May be all negative
c)
May be all non-negative
d)
May be positive for some cases and negative in other cases
|
|
Mira Sharma answered |
The y coordinates of the particles of the body may be all non zero and positive for some cases and negative in other cases.
If the external forces acting on a system have zero resultant, the centre of mass- a) Must not move
- b)Must not accelerate
- c)May move
- d)May accelerate
Correct answer is option 'B,C'. Can you explain this answer?
If the external forces acting on a system have zero resultant, the centre of mass
a)
Must not move
b)
Must not accelerate
c)
May move
d)
May accelerate

|
Priyanka Roy answered |
If the external force acting on a system have zero resultant, then the total momentum remain . constant i.e conserved. Hence, the center of mass remains at rest or move with a constant velocity.
In which of the following cases the centre of mass of a an rod is certainly not at its centre ?- a)The density continuously increases from left to right
- b)The density continuously decreases from left to right
- c)The density decreases from left to right upto the centre and then increase
- d)The density increases from left to right upto the centre and then decreases
Correct answer is option 'A,B'. Can you explain this answer?
In which of the following cases the centre of mass of a an rod is certainly not at its centre ?
a)
The density continuously increases from left to right
b)
The density continuously decreases from left to right
c)
The density decreases from left to right upto the centre and then increase
d)
The density increases from left to right upto the centre and then decreases
|
|
Pallabi Rane answered |
- It can’t be since the integral would yield a value much greater than R/2
- It can’t be since the integral would yield a value much less than R/2
- Assuming the rate of increase and decrease is same the COM could lie in the centre
- Assuming the rate of increase and decrease is same the COM could lie in the centre
Suppose a moving truck with mass m1 and a velocity v1 collides with a moving convertible with mass m2 and velocity v2 resulting in both coming to a complete stop, where m1 is three times the value of m2 and v2 is three times v1. The truck collides with the convertible with a force F1. Which of the following statements accurately describes the resultant force F2 of the convertible?- a)The convertible exerts the same force on the truck.
- b)The convertible exerts a smaller force because of its smaller mass.
- c)The force gets dissipated during the collision in the form of heat, sound, and deformation of the two vehicles.
- d)The convertible exerts a larger force because of its greater velocity.
Correct answer is option 'A'. Can you explain this answer?
Suppose a moving truck with mass m1 and a velocity v1 collides with a moving convertible with mass m2 and velocity v2 resulting in both coming to a complete stop, where m1 is three times the value of m2 and v2 is three times v1. The truck collides with the convertible with a force F1. Which of the following statements accurately describes the resultant force F2 of the convertible?
a)
The convertible exerts the same force on the truck.
b)
The convertible exerts a smaller force because of its smaller mass.
c)
The force gets dissipated during the collision in the form of heat, sound, and deformation of the two vehicles.
d)
The convertible exerts a larger force because of its greater velocity.

|
Orion Classes answered |
- Whether the convertible exerts a smaller force because of its smaller mass cannot be determined since it has a greater change in velocity and therefore, acceleration to offset its smaller mass.
- Whether the convertible exerts a larger force because of its greater velocity cannot be determined since the truck has a larger mass despite its smaller velocity. It would take more work to stop the convertible due its higher velocity.
- It is the energy of the collision that gets dissipated in the form of heat, sound, and deformation of the two vehicles, not the force.
- They exert the same force on each other is correct. Due to Newton’s Third Law, if the truck collides with force F, then the SUV collides with force -F, equal in magnitude opposite in direction.
- Additionally, their momentums are equal, so that their impulses are equal. Therefore, the time of the collision is the same for both, so the average force of impact is the same.
There is a force F acting on an object of mass m, which has an acceleration a. If the mass is doubled and the force is reduced by a factor of four, what is the acceleration of the new object?- a)a
- b)1/8 a
- c)1/2 a
- d)2a
Correct answer is option 'B'. Can you explain this answer?
There is a force F acting on an object of mass m, which has an acceleration a. If the mass is doubled and the force is reduced by a factor of four, what is the acceleration of the new object?
a)
a
b)
1/8 a
c)
1/2 a
d)
2a

|
Orion Classes answered |
- Acceleration is directly proportional to force and inversely proportional to mass: F = ma.
- If mass is doubled, acceleration would be halved: F = 2m(½a).
- If force is reduced by four, acceleration would be reduced by four: ¼F = m(¼a).
- In total, the acceleration decreases by a factor of 8: ¼F = 2m(⅛a) = ¼(ma).
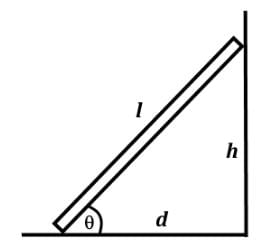
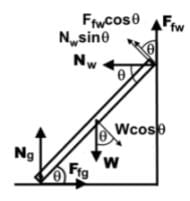
A ladder of length l of 6 meters is propped up on the wall at a height h of 5.1 meters above the ground. The bottom of the ladder is positioned at a distance d of 3 meters from the wall. There are static frictional forces at the wall and the ground that keep the ladder in place. Which of the following force components creates a positive torque if the fulcrum is placed at the bottom of the ladder? (FNW = normal force from wall, FNG = normal force from ground, FFW = friction force at wall, FFG = friction force at ground)
- a)FNW sinθ
- b)FNG cosθ
- c)W cosθ
- d)FFW sinθ
Correct answer is option 'A'. Can you explain this answer?
A ladder of length l of 6 meters is propped up on the wall at a height h of 5.1 meters above the ground. The bottom of the ladder is positioned at a distance d of 3 meters from the wall. There are static frictional forces at the wall and the ground that keep the ladder in place. Which of the following force components creates a positive torque if the fulcrum is placed at the bottom of the ladder? (FNW = normal force from wall, FNG = normal force from ground, FFW = friction force at wall, FFG = friction force at ground)


a)
FNW sinθ
b)
FNG cosθ
c)
W cosθ
d)
FFW sinθ

|
Orion Classes answered |
- All forces need to be resolved along the plane of the ladder such that it becomes the x-axis and the y-axis perpendicular to that, like on an inclined plane.
- Since the fulcrum is placed at the bottom of the ladder and FNG acts at the fulcrum, it is not considered to produce a torque.
- FNW points directly outward from the wall to the left. FNW cosθ is along the plane of the ladder, so FNW sin θ is the force that would create a positive or counterclockwise torque on the ladder.
- FFW points from the contact point of the ladder on the wall upwards along the wall. FNW sin θ is the force component that is along the plane of the ladder pointing into the wall. FFW cos θ would be the force that creates a counterclockwise torque.
- W points downward from the center of the ladder. Wcosθ is perpendicular to the plane of the ladder and creates a clockwise torque on the ladder.
- Here is a diagram illustrating all the forces creating the torque:
Two blocks A (5kg) and B(2kg) attached to the ends of a spring constant 1120 N/m are placed on a smooth horizontal plane with the spring undeformed. Simultaneously velocities of 3m/s and 10m/s along the line of the spring in the same direction are imparted to A and B then 
- a)When the extension of the spring is maximum the velocities of A and B are zero.
- b)The maximum extension of the spring is 25 cm
- c)Maximum extension and maximum compression occur alternately.
- d)The maximum compression occur for the first time after
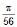 sec.
sec.
Correct answer is option 'B,C'. Can you explain this answer?
Two blocks A (5kg) and B(2kg) attached to the ends of a spring constant 1120 N/m are placed on a smooth horizontal plane with the spring undeformed. Simultaneously velocities of 3m/s and 10m/s along the line of the spring in the same direction are imparted to A and B then
a)
When the extension of the spring is maximum the velocities of A and B are zero.
b)
The maximum extension of the spring is 25 cm
c)
Maximum extension and maximum compression occur alternately.
d)
The maximum compression occur for the first time after 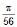 sec.
sec.
|
|
Akshara Gupta answered |
Vcm = m1v1 + m2v2/m1 + m2 = 5m/s
So, Vrela = -2m/s and Vrelb = 5m/s
Now, Va = 5m/s and Vb = 5m/s
Also, ½ K x2max = ½ μ V2rel
So, xmax = ¼ m = 25 cm
Now, since the time periods of both the blocks are same so they will be at max compression and elongation alternatively
So, Vrela = -2m/s and Vrelb = 5m/s
Now, Va = 5m/s and Vb = 5m/s
Also, ½ K x2max = ½ μ V2rel
So, xmax = ¼ m = 25 cm
Now, since the time periods of both the blocks are same so they will be at max compression and elongation alternatively
A particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.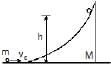 The final velocity of the wedge v2 is
The final velocity of the wedge v2 is- a)

- b)
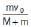
- c)v0
- d)insufficient data
Correct answer is option 'B'. Can you explain this answer?
A particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
The final velocity of the wedge v2 is
a)
b)
c)
v0
d)
insufficient data

|
Thor Clush answered |

Block 1 with mass m1 sits on top of Block 2 with mass m2. While m1 is greater than m2, they have an identical length L. Which of the following statements accurately describes the torques in this two-block system?
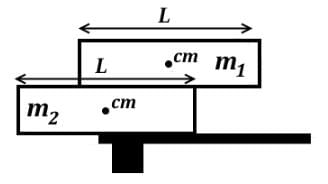
- a)If Block 1 were shifted to the right the increasing clockwise torque on Block 1 is balanced by an increasing normal force on Block 1.
- b)If Block 2 were shifted to the left along with Block 1 without toppling off, the weight of block 2 would create a clockwise torque that is offset by the weight of Block 1 which creates a counterclockwise torque.
- c)The weight of Block 1 through its center of mass produces a clockwise torque about the right end of Block 2.
- d)The normal force on Block 1 produces a clockwise torque and the weight of Block 1 is producing a counterclockwise torque with the fulcrum at the right end of Block 1.
Correct answer is option 'D'. Can you explain this answer?
Block 1 with mass m1 sits on top of Block 2 with mass m2. While m1 is greater than m2, they have an identical length L. Which of the following statements accurately describes the torques in this two-block system?


a)
If Block 1 were shifted to the right the increasing clockwise torque on Block 1 is balanced by an increasing normal force on Block 1.
b)
If Block 2 were shifted to the left along with Block 1 without toppling off, the weight of block 2 would create a clockwise torque that is offset by the weight of Block 1 which creates a counterclockwise torque.
c)
The weight of Block 1 through its center of mass produces a clockwise torque about the right end of Block 2.
d)
The normal force on Block 1 produces a clockwise torque and the weight of Block 1 is producing a counterclockwise torque with the fulcrum at the right end of Block 1.

|
Orion Classes answered |
- If the force acts downwards to the left or upwards to the right of the fulcrum, then there is a counterclockwise (CCW) torque. If the force acts downwards to the right or upwards to the left of the fulcrum, then there is a clockwise (CW) torque.
- Forces will act from the center of mass if possible, and the fulcrums are the top right edge of Block 2 and the left edge of the desk.
- If Block 2 were shifted to the left, the center of mass moves to the left of the fulcrum, so the weight creates a CCW torque, not CW. The weight of Block 1 acts to the right of the same fulcrum downwards creating a CW torque, not CCW.
- If Block 1 were shifted to the right, as the center of mass moves to the right of the fulcrum, it will create a CW torque that topples off Block 1. However, the small normal force from Block 2 has been decreasing as Block 1 moved to the right.
- The weight of Block 1 acts to the left of the fulcrum downwards, and the weight will produce a CCW torque, not CW.
- There is a normal force from Block 2 on Block 1 that acts to the left of the fulcrum upwards, producing a CW torque.
- Here is a diagram indicating the forces:
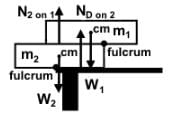
Suppose the particle when reaches the horizontal surfaces, its velocity with respect to ground is v1 and that of wedge is v2. Choose the correct statement (s) 
- a) mv1 = Mv2
- b)Mv2 _ mv1 = mv0
- c)v1 + v2 = v0
- d)v1 + v2 < v0
Correct answer is option 'B,C'. Can you explain this answer?
Suppose the particle when reaches the horizontal surfaces, its velocity with respect to ground is v1 and that of wedge is v2. Choose the correct statement (s)
a)
mv1 = Mv2
b)
Mv2 _ mv1 = mv0
c)
v1 + v2 = v0
d)
v1 + v2 < v0

|
Famous Places, answered |
Please send me the solution of this question
Tension in string when it is vertical, is- a) Mg
- b)Mg(2 _ cosq)
- c) Mg (3 _ 2 cosq)
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Tension in string when it is vertical, is
a)
Mg
b)
Mg(2 _ cosq)
c)
Mg (3 _ 2 cosq)
d)
None of these
|
|
Sagar Goyal answered |
Tension in string when it is vertical, is Mg. Since nothing else has been provided so we assume all the forces are in the desired directions.
Identify the correct statement(s) related to the situation when the particle starts moving downward.- a)The centre of mass of the system remains stationary
- b)Both the particle and the wedge remain stationary with respect to centre of mass
- c)When the particle reaches the horizontal surface its velocity relative to the wedge is v0
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Identify the correct statement(s) related to the situation when the particle starts moving downward.
a)
The centre of mass of the system remains stationary
b)
Both the particle and the wedge remain stationary with respect to centre of mass
c)
When the particle reaches the horizontal surface its velocity relative to the wedge is v0
d)
None of these
|
|
Akash Chakraborty answered |
Explanation:
When the particle starts moving downward, there are certain changes that occur in the system. Let's discuss these changes in detail:
Centre of Mass of the System:
The centre of mass of the system is the point where the entire mass of the system is assumed to be concentrated. In this case, the system consists of a wedge and a particle. When the particle starts moving downward, its position changes, which means the centre of mass of the system also changes. Hence, option 'A' is incorrect.
Position of the Wedge:
As the particle starts moving downward, it exerts a force on the wedge in the backward direction. According to Newton's third law of motion, the wedge also exerts an equal and opposite force on the particle in the forward direction. This force causes the wedge to move forward, and its position changes with respect to the ground. Hence, option 'B' is incorrect.
Velocity of the Particle:
When the particle reaches the horizontal surface, its velocity relative to the wedge is v0. This is because the wedge and the particle are moving in the same direction with the same velocity. Hence, option 'C' is correct.
Conclusion:
When the particle starts moving downward, the centre of mass of the system changes, and the position of the wedge also changes. However, when the particle reaches the horizontal surface, its velocity relative to the wedge is v0.
When the particle starts moving downward, there are certain changes that occur in the system. Let's discuss these changes in detail:
Centre of Mass of the System:
The centre of mass of the system is the point where the entire mass of the system is assumed to be concentrated. In this case, the system consists of a wedge and a particle. When the particle starts moving downward, its position changes, which means the centre of mass of the system also changes. Hence, option 'A' is incorrect.
Position of the Wedge:
As the particle starts moving downward, it exerts a force on the wedge in the backward direction. According to Newton's third law of motion, the wedge also exerts an equal and opposite force on the particle in the forward direction. This force causes the wedge to move forward, and its position changes with respect to the ground. Hence, option 'B' is incorrect.
Velocity of the Particle:
When the particle reaches the horizontal surface, its velocity relative to the wedge is v0. This is because the wedge and the particle are moving in the same direction with the same velocity. Hence, option 'C' is correct.
Conclusion:
When the particle starts moving downward, the centre of mass of the system changes, and the position of the wedge also changes. However, when the particle reaches the horizontal surface, its velocity relative to the wedge is v0.
A ball moving with a velocity v hits a massive wall moving towards the ball with a velocity u. An elastic impact lasts for a time Dt.- a)The average elastic force acting on the ball is
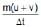
- b)The average elastic force acting on the ball is
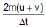
- c)The kinetic energy of the ball increases by 2mu (u + v)
- d)The kinetic energy of the ball remains the same after the collision.
Correct answer is option 'B,C'. Can you explain this answer?
A ball moving with a velocity v hits a massive wall moving towards the ball with a velocity u. An elastic impact lasts for a time Dt.
a)
The average elastic force acting on the ball is 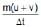
b)
The average elastic force acting on the ball is 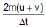
c)
The kinetic energy of the ball increases by 2mu (u + v)
d)
The kinetic energy of the ball remains the same after the collision.
|
|
Ishani Pillai answered |
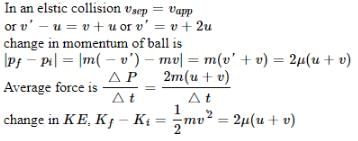
Chapter doubts & questions for Force (PHY) - MCAT Chemical and Physical Foundations 2025 is part of MCAT exam preparation. The chapters have been prepared according to the MCAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for MCAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Force (PHY) - MCAT Chemical and Physical Foundations in English & Hindi are available as part of MCAT exam.
Download more important topics, notes, lectures and mock test series for MCAT Exam by signing up for free.
MCAT Chemical and Physical Foundations
336 videos|223 docs|109 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup