All questions of Theory of Computation for Computer Science Engineering (CSE) Exam
Which of the following statements is true?- a)If a language is context free it can always be accepted by a deterministic push-down automaton
- b)The union of two context free languages is context free
- c)The intersection of two contest free languages is a context free
- d)The complement of a context free language is a context free
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is true?
a)
If a language is context free it can always be accepted by a deterministic push-down automaton
b)
The union of two context free languages is context free
c)
The intersection of two contest free languages is a context free
d)
The complement of a context free language is a context free
|
Ravi Singh answered |
(A) is wrong as a language can be context free even if it is being accepted by non deterministic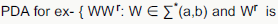 
reverse}
(C) and (D) not always true as Context free languages are not closed under Complement and Intersection.
Over the alphabet , {0,1} consider the language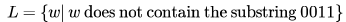
Which of the following is true about L.- a)L is not context free
- b)L is regular
- c)L is not regular but it is context free
- d)L is context free but not recursively enumerable
Correct answer is option 'B'. Can you explain this answer?
Over the alphabet , {0,1} consider the language
Which of the following is true about L.
a)
L is not context free
b)
L is regular
c)
L is not regular but it is context free
d)
L is context free but not recursively enumerable
|
Raj Sen answered |
L is regular.
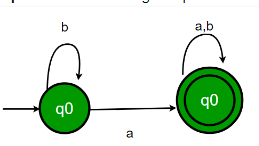
Consider the following Finite State Automaton: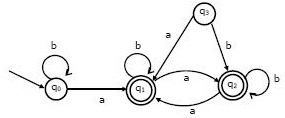
The language accepted by this automaton is given by the regular expression- a) b∗ab∗ab∗ab∗
- b) (a+b)∗
- c) b∗a(a+b)∗
- d) b∗ab∗ab∗
Correct answer is option 'C'. Can you explain this answer?
Consider the following Finite State Automaton:
The language accepted by this automaton is given by the regular expression
a)
b∗ab∗ab∗ab∗
b)
(a+b)∗
c)
b∗a(a+b)∗
d)
b∗ab∗ab∗
|
|
Ravi Singh answered |
- In this case, we would at least have to reach q1 so that our string gets accepted. So, b* a is the smallest accepted string.
- Now, at q1, any string with any number of a’s and b’s would be accepted. So, we append (a + b)* to the smallest accepted string.
- Thus, the string accepted by the FSA is b* a(a + b)*.
Thus, C is the correct choice.
The language accepted by a Pushdown Automation in which the stack is limited to 10 items is best described as- a)Context Free
- b)Regular
- c)Deterministic Context Free
- d)Recursive
Correct answer is option 'B'. Can you explain this answer?
The language accepted by a Pushdown Automation in which the stack is limited to 10 items is best described as
a)
Context Free
b)
Regular
c)
Deterministic Context Free
d)
Recursive
|
|
Ravi Singh answered |
Pushdown automata is used for context free languages, i.e., languages in which the length of elements is unrestricted and length of one element is related to other. To resolve this problem, we use a stack with no restrictions on length.
But in the given case, length of stack is restricted. Thus, this pushdown automata can only accept languages which can also be accepted by finite state automata and a finite state automata accepts only regular languages.
Thus, B is the correct choice.
Please comment below if you find anything wrong in the above post.
But in the given case, length of stack is restricted. Thus, this pushdown automata can only accept languages which can also be accepted by finite state automata and a finite state automata accepts only regular languages.
Thus, B is the correct choice.
Please comment below if you find anything wrong in the above post.
Consider the following languages.
L1 = {ai bj ck | i = j, k ≥ 1}
L1 = {ai bj | j = 2i, i ≥ 0}
Q. Which of the following is true?- a)L1 is not a CFL but L2 is
- b)L1 ∩ L2 = ∅ and L1 is non-regular
- c)L1 ∪ L2 is not a CFL but L2 is
- d)There is a 4-state PDA that accepts L1, but there is no DPDA that accepts L2
Correct answer is option 'B'. Can you explain this answer?
Consider the following languages.
L1 = {ai bj ck | i = j, k ≥ 1}
L1 = {ai bj | j = 2i, i ≥ 0}
Q. Which of the following is true?
L1 = {ai bj ck | i = j, k ≥ 1}
L1 = {ai bj | j = 2i, i ≥ 0}
Q. Which of the following is true?
a)
L1 is not a CFL but L2 is
b)
L1 ∩ L2 = ∅ and L1 is non-regular
c)
L1 ∪ L2 is not a CFL but L2 is
d)
There is a 4-state PDA that accepts L1, but there is no DPDA that accepts L2
|
Kabir Verma answered |
A: Both L1 and L2 are CFL
B: L1 ∩ L2 = ∅ is true
L1is not regular => true
=> B is true
C: L1 ∪ L2 is not a CFL nut L2 is CFL is closed under Union
=> False
D: Both L1 and L2 accepted by DPDA
B: L1 ∩ L2 = ∅ is true
L1is not regular => true
=> B is true
C: L1 ∪ L2 is not a CFL nut L2 is CFL is closed under Union
=> False
D: Both L1 and L2 accepted by DPDA
Let L1 be a recursive language. Let L2 and L3 be languages that are recursively enumerable but not recursive.
Which of the following statements is not necessarily true? - a)L2 – L1 is recursively enumerable
- b)L1 – L3 is recursively enumerable
- c)L2 ∩ L1 is recursively enumerable
- d)L2 ∪ L1 is recursively enumerable
Correct answer is option 'B'. Can you explain this answer?
Let L1 be a recursive language. Let L2 and L3 be languages that are recursively enumerable but not recursive.
Which of the following statements is not necessarily true?
Which of the following statements is not necessarily true?
a)
L2 – L1 is recursively enumerable
b)
L1 – L3 is recursively enumerable
c)
L2 ∩ L1 is recursively enumerable
d)
L2 ∪ L1 is recursively enumerable
|
Avinash Mehta answered |
ANSWER B L1−L3=L1∩L3
Recursively enumerable languages are not closed under complement. So, L3 may or may not be recursively enumerable and hence we can't say anything if L1∩L3 is recursively enumerable or not.
Which two of the following four regular expressions are equivalent? (ε is the empty string).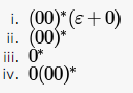
- a)(i) and (ii)
- b)(ii) and (iii)
- c)(i) and (iii)
- d)(iii) and (iv)
Correct answer is option 'C'. Can you explain this answer?
Which two of the following four regular expressions are equivalent? (ε is the empty string).
a)
(i) and (ii)
b)
(ii) and (iii)
c)
(i) and (iii)
d)
(iii) and (iv)
|
|
Ravi Singh answered |
you can have any no. of 0's as well as null.
A is false because you cannot have single 0 in ii). same for option B. In D you are forced to have single 0 in iv) whereas not in iii).
A is false because you cannot have single 0 in ii). same for option B. In D you are forced to have single 0 in iv) whereas not in iii).
Let B consist of all binary strings beginning with a 1 whose value when converted to decimal is divisible by 7 .- a)B can be recognized by a deterministic finite state automaton.
- b)B can be recognized by a non-deterministic finite state automaton but not by a deterministic finite state automaton.
- c)B can be recognized by a deterministic push-down automaton but not by a non-deterministic finite state automaton.
- d)B can be recognized by a non-deterministic push-down automaton but not by a deterministic push-down automaton.
- e)B cannot be recognized by any push down automaton, deterministic or non-deterministic.
Correct answer is option 'A'. Can you explain this answer?
Let B consist of all binary strings beginning with a 1 whose value when converted to decimal is divisible by 7 .
a)
B can be recognized by a deterministic finite state automaton.
b)
B can be recognized by a non-deterministic finite state automaton but not by a deterministic finite state automaton.
c)
B can be recognized by a deterministic push-down automaton but not by a non-deterministic finite state automaton.
d)
B can be recognized by a non-deterministic push-down automaton but not by a deterministic push-down automaton.
e)
B cannot be recognized by any push down automaton, deterministic or non-deterministic.
|
Yash Patel answered |
if it start with 1 it goes to final state
if start with 0 it will go to the reject state
Consider the languages L1 = {0i1j | i != j}. L2 = {0i1j | i = j}. L3 = {0i1j | i = 2j+1}. L4 = {0i1j | i != 2j}.- a)Only L2 is context free
- b)Only L2 and L3 are context free
- c)Only L1 and L2 are context free
- d)All are context free
Correct answer is option 'D'. Can you explain this answer?
Consider the languages L1 = {0i1j | i != j}. L2 = {0i1j | i = j}. L3 = {0i1j | i = 2j+1}. L4 = {0i1j | i != 2j}.
a)
Only L2 is context free
b)
Only L2 and L3 are context free
c)
Only L1 and L2 are context free
d)
All are context free
|
Pathways Academy answered |
All these languages have valid CFGs that can derive them. Hence, all of them are CFLs. Intuitively, (A) & (B) are well known CFLs and CFGs for (C) & (D) could be made by little modifications in A & B’s CFGs.
Let < M > be the encoding of a Turing machine as a string over {0, 1}. Let L = { < M > |M is a Turing machine that accepts a string of length 2014 }. Then, L is- a)decidable and recursively enumerable
- b)undecidable but recursively enumerable
- c)undecidable and not recursively enumerable
- d)decidable but not recursively enumerable
Correct answer is option 'B'. Can you explain this answer?
Let < M > be the encoding of a Turing machine as a string over {0, 1}. Let L = { < M > |M is a Turing machine that accepts a string of length 2014 }. Then, L is
a)
decidable and recursively enumerable
b)
undecidable but recursively enumerable
c)
undecidable and not recursively enumerable
d)
decidable but not recursively enumerable
|
|
Aditya Deshmukh answered |
There are finite number of strings of length ‘2014’. So, a turing machine will take the input string of length ‘2014’ and test it.
If, input string is present in the language then turing machine will halt in final state .
But, if turing machine is unable to accept the input string then it will halt in non-final state or go in an infinite loop and never halt.
Thus, ‘L’ is undecidable and recursively enumerable .
Let w be a string and fragmented by three variable x, y, and z as per pumping lemma. What does these variables represent?- a)string count
- b)string
- c)string count and string
- d)none of the mentioned
Correct answer is option 'A'. Can you explain this answer?
Let w be a string and fragmented by three variable x, y, and z as per pumping lemma. What does these variables represent?
a)
string count
b)
string
c)
string count and string
d)
none of the mentioned
|
Sudhir Patel answered |
Given: w =xyz. Here, xyz individually represents strings or rather substrings which we compute over conditions to check the regularity of the language.
Answer in accordance to the third and last statement in pumping lemma:For all _______ xyiz ∈L- a)i>0
- b)i<0
- c)i<=0
- d)i>=0
Correct answer is option 'D'. Can you explain this answer?
Answer in accordance to the third and last statement in pumping lemma:For all _______ xyiz ∈L
a)
i>0
b)
i<0
c)
i<=0
d)
i>=0
|
Abhijeet Unni answered |
For all xyiz, where |xy| ≤ p and |y| > 0, there exists a string w ∈ L such that w can be divided into three parts, w = xyz, satisfying the following conditions:
1. For each i ≥ 0, xyiz ∈ L.
2. |xy| ≤ p.
3. |y| > 0.
1. For each i ≥ 0, xyiz ∈ L.
2. |xy| ≤ p.
3. |y| > 0.
Which of the following is TRUE?- a)Every subset of a regular set is regular
- b)Every finite subset of a non-regular set is regular
- c)The union of two non-regular sets is not regular
- d)Infinite union of finite sets is regular
Correct answer is option 'B'. Can you explain this answer?
Which of the following is TRUE?
a)
Every subset of a regular set is regular
b)
Every finite subset of a non-regular set is regular
c)
The union of two non-regular sets is not regular
d)
Infinite union of finite sets is regular
|
|
Yash Patel answered |
(B) Every finite subset of a non-regular set is regular.
Any finite set is always regular.
Any finite set is always regular.
∑* being regular any non regular language is a subset of this, and hence (A) is false.
If we take a CFL which is not regular, and takes union with its complement (complement of a CFL which is not regular won't be regular as regular is closed under complement), we get ∑* which is regular. So, (C) is false.
Regular set is not closed under infinite union. Example: Let Li = {0i1i }, i ∊ N
Now, if we take infinite union over all i, we get
L = {0i1i | i ∊ N}, which is not regular. So, D is false.
A language L satisfies the Pumping Lemma for regular languages, and also the Pumping Lemma for context-free languages. Which of the following statements about L is TRUE? - a)L is necessarily a regular language.
- b)L is necessarily a context-free language, but not necessarily a regular language
- c)L is necessarily a non-regular language
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
A language L satisfies the Pumping Lemma for regular languages, and also the Pumping Lemma for context-free languages. Which of the following statements about L is TRUE?
a)
L is necessarily a regular language.
b)
L is necessarily a context-free language, but not necessarily a regular language
c)
L is necessarily a non-regular language
d)
None of the above
|
Neha Choudhury answered |
Pumping lemma is negativity test. We use it to disprove that a languages is not regular. But reverse is not true.
Which one of the following languages over the alphabet {0,1} is described by the regular expression: (0 + 1)*0(0 + 1)*0(0 + 1)*?- a)The set of all strings containing the substring 00
- b)The set of all strings containing at most two 0's
- c) The set of all strings containing at least two 0's
- d)The set of all strings that begin and end with either 0 or 1
Correct answer is option 'C'. Can you explain this answer?
Which one of the following languages over the alphabet {0,1} is described by the regular expression: (0 + 1)*0(0 + 1)*0(0 + 1)*?
a)
The set of all strings containing the substring 00
b)
The set of all strings containing at most two 0's
c)
The set of all strings containing at least two 0's
d)
The set of all strings that begin and end with either 0 or 1
|
|
Yash Patel answered |
Counter example for other choices:
(A) 1010 is accepted which doesn't contain 00
(B) 000 is accepted
(D) 01 is not accepted
Let w= xyz and y refers to the middle portion and |y|>0.What do we call the process of repeating y 0 or more times before checking that they still belong to the language L or not?- a)Generating
- b)Pumping
- c)Producing
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Let w= xyz and y refers to the middle portion and |y|>0.What do we call the process of repeating y 0 or more times before checking that they still belong to the language L or not?
a)
Generating
b)
Pumping
c)
Producing
d)
None of the mentioned
|
|
Sudhir Patel answered |
The process of repeatation is called pumping and so, pumping is the process we perform before we check whether the pumped string belongs to L or not.
Which of the following statements is false?- a)Every NFA can be converted to an equivalent DFA
- b)Every non-deterministic Turing machine can be converted to an equivalent deterministic Turing machine
- c)Every subset of a recursively enumerable set is recursive
- d)none
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is false?
a)
Every NFA can be converted to an equivalent DFA
b)
Every non-deterministic Turing machine can be converted to an equivalent deterministic Turing machine
c)
Every subset of a recursively enumerable set is recursive
d)
none
|
Bijoy Sharma answered |
A language is recursively enumerable if there exists a Turing machine that accepts every string of the language, and does not accept strings that are not in the language. Strings that are not in the language may be rejected or may cause the Turing machine to go into an infinite loop.
A recursive language can't go into an infinite loop, it has to clearly reject the string, but a recursively enumerable language can go into an infinite loop.
So, every recursive language is also recursively enumerable. Thus, the statement ‘Every subset of a recursively enumerable set is recursive’ is false.
Thus, option (C) is the answer.
A recursive language can't go into an infinite loop, it has to clearly reject the string, but a recursively enumerable language can go into an infinite loop.
So, every recursive language is also recursively enumerable. Thus, the statement ‘Every subset of a recursively enumerable set is recursive’ is false.
Thus, option (C) is the answer.
Consider the Following regular expressionsr1 = 1(0 + 1)*
r2 = 1(1 + 0)+
r3 = 11*0Q. What is the relation between the languages generated by the regular expressions above ?- a)L (r1) ⊆ L (r2) and L(r1) ⊆ L(r3)
- b)L (r1) ⊇ L (r2) and L(r2) ⊇ L(r3)
- c)L (r1) ⊇ L (r2) and L(r2) ⊆ L(r3)
- d)L (r1) ⊇ L (r3) and L(r2) ⊆ L(r1)
Correct answer is option 'B'. Can you explain this answer?
Consider the Following regular expressions
r1 = 1(0 + 1)*
r2 = 1(1 + 0)+
r3 = 11*0
r2 = 1(1 + 0)+
r3 = 11*0
Q. What is the relation between the languages generated by the regular expressions above ?
a)
L (r1) ⊆ L (r2) and L(r1) ⊆ L(r3)
b)
L (r1) ⊇ L (r2) and L(r2) ⊇ L(r3)
c)
L (r1) ⊇ L (r2) and L(r2) ⊆ L(r3)
d)
L (r1) ⊇ L (r3) and L(r2) ⊆ L(r1)
|
Mrinalini Menon answered |
Clearly r1 is a superset of both r2 and r3 as string 1 can not be generated by r2 and r3. r2 is a superset of r3 as string 11 is not present in L(r3) but in L(r2).
Let G = ({S}, {a, b} R, S) be a context free grammar where the rule set R is S → a S b | SS | ε Which of the following statements is true?- a)G is not ambiguous
- b)There exist x, y, ∈ L (G) such that xy ∉ L(G)
- c)There is a deterministic pushdown automaton that accepts L(G)
- d)We can find a deterministic finite state automaton that accepts L(G)
Correct answer is option 'C'. Can you explain this answer?
Let G = ({S}, {a, b} R, S) be a context free grammar where the rule set R is S → a S b | SS | ε Which of the following statements is true?
a)
G is not ambiguous
b)
There exist x, y, ∈ L (G) such that xy ∉ L(G)
c)
There is a deterministic pushdown automaton that accepts L(G)
d)
We can find a deterministic finite state automaton that accepts L(G)
|
|
Ravi Singh answered |
An ambiguous grammar can be converted to unambiguous one.
Here we can get grammar in partial GNF form as S -> ab | abS | aSb | aSbS
We can convert this into GNF too but no need for PDA reasoning so, above grammar is not a ambiguous thus a definite PDA possible
Trick for this is but just deriving 3-4 strings from grammar, we can easily understand its (anbn)* above expression anbn is in CFL thus closure of DCFG is a DCFG i.e., you can get L = {ε, ab, abab, aabb, aabbab, abaabb, ababab,......}
PDA will push "a" until "b" is read, start popping "a" for the "b" read.
If "a" is read again from the tape then push only when stack is empty else terminate.
Repeat this until string is read. Remember fastest way to get answer is by elimination other options.
Here we can get grammar in partial GNF form as S -> ab | abS | aSb | aSbS
We can convert this into GNF too but no need for PDA reasoning so, above grammar is not a ambiguous thus a definite PDA possible
Trick for this is but just deriving 3-4 strings from grammar, we can easily understand its (anbn)* above expression anbn is in CFL thus closure of DCFG is a DCFG i.e., you can get L = {ε, ab, abab, aabb, aabbab, abaabb, ababab,......}
PDA will push "a" until "b" is read, start popping "a" for the "b" read.
If "a" is read again from the tape then push only when stack is empty else terminate.
Repeat this until string is read. Remember fastest way to get answer is by elimination other options.
Which one of the following regular expressions represents the language: the set of all binary strings having two consecutive 0's and two consecutive 1's?- a)
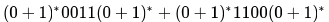
- b)
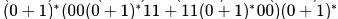
- c)
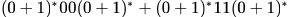
- d)
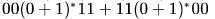
Correct answer is option 'B'. Can you explain this answer?
Which one of the following regular expressions represents the language: the set of all binary strings having two consecutive 0's and two consecutive 1's?
a)
b)
c)
d)
|
|
K I N G answered |
Option A represents those strings which either have 0011 or 1100 as substring.
Option C represents those strings which either have 00 or 11 as substring.
Option D represents those strings which start with 11 and end with 00 or start with 00 and end with 11.
Option C represents those strings which either have 00 or 11 as substring.
Option D represents those strings which start with 11 and end with 00 or start with 00 and end with 11.
The language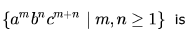 
- a)regular
- b)context-free but not regular
- c)context-sensitive but not context free
- d)type-0 but not context sensitive
Correct answer is option 'B'. Can you explain this answer?
The language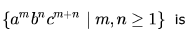
a)
regular
b)
context-free but not regular
c)
context-sensitive but not context free
d)
type-0 but not context sensitive
|
|
Pallavi Reddy answered |
Language is not regular bcoz we need to match count of c's is equal to count of b's + count of a's
and that can implement by PDA
∂(q0,a,^)= (q0,a) [ push a in stack, as per language a comes first]
∂(q0,a,a)= (q0,aa) [push all a's into stack]
∂(q0,b,a) = (q1,ba) [push b in stack, state change to q1 that sure b comes after a]
∂(q1,b,b)=(q1,bb) [push all b's in stack]
∂(q1,c,b) = (q2,^) [ pop one b for one c]
∂(q0,b,a) = (q1,ba) [push b in stack, state change to q1 that sure b comes after a]
∂(q1,b,b)=(q1,bb) [push all b's in stack]
∂(q1,c,b) = (q2,^) [ pop one b for one c]
∂(q2,c,b) = (q2,c) [ pop one b's for each c and continue same ]
∂(q2,c,a) = (q3,^) [ pop one a for one c , when there is no more b in stack]
∂(q3,c,a) = (q3,^) [pop one a for each c and continue same]
∂(q3,^,^) = (qf,^) [ if sum of c's is sum of a's and b's then stack will be empty when there is no c in input]
∂(q2,c,a) = (q3,^) [ pop one a for one c , when there is no more b in stack]
∂(q3,c,a) = (q3,^) [pop one a for each c and continue same]
∂(q3,^,^) = (qf,^) [ if sum of c's is sum of a's and b's then stack will be empty when there is no c in input]
Note :1. state changes make sure b's comes after a and c's comes after b's]
Suppose M1 and M2 are two TM’s such that L(M1) = L(M2). Then- a)On every input on which M1 doesn’t halt, M2 doesn’t halt too.
- b)On every i/p on which M1 halts, M2 halts too.
- c)On every i/p which M1 accepts, M2 halts.
- d)None of above
Correct answer is option 'C'. Can you explain this answer?
Suppose M1 and M2 are two TM’s such that L(M1) = L(M2). Then
a)
On every input on which M1 doesn’t halt, M2 doesn’t halt too.
b)
On every i/p on which M1 halts, M2 halts too.
c)
On every i/p which M1 accepts, M2 halts.
d)
None of above
|
|
Dipika Chavan answered |
Explanation:
To understand why option 'C' is the correct answer, let's analyze each option one by one.
a) On every input on which M1 doesn't halt, M2 doesn't halt too.
This statement is not necessarily true. Just because M1 doesn't halt on a particular input, it doesn't mean that M2 will also not halt on the same input. The Turing machines M1 and M2 can have different behaviors on inputs where they don't halt.
b) On every input on which M1 halts, M2 halts too.
This statement is also not necessarily true. Even though M1 and M2 accept the same language, it doesn't imply that they have the same halting behavior. M2 may halt on inputs where M1 halts, but it may also halt on additional inputs that are not accepted by M1.
c) On every input which M1 accepts, M2 halts.
This statement is true. Since M1 and M2 accept the same language, if M1 accepts an input, it means that the input belongs to the language. Since M2 also accepts the same language, it must halt on the same input. If M2 didn't halt on an input that M1 accepted, then M2 would not accept the language L(M1) = L(M2), which contradicts the given condition.
d) None of the above.
This option can be eliminated as we have already determined that option 'C' is the correct answer.
Conclusion:
The correct answer is option 'C'. On every input that is accepted by M1, M2 will halt as well. This is because both Turing machines accept the same language. However, the other options are not necessarily true.
To understand why option 'C' is the correct answer, let's analyze each option one by one.
a) On every input on which M1 doesn't halt, M2 doesn't halt too.
This statement is not necessarily true. Just because M1 doesn't halt on a particular input, it doesn't mean that M2 will also not halt on the same input. The Turing machines M1 and M2 can have different behaviors on inputs where they don't halt.
b) On every input on which M1 halts, M2 halts too.
This statement is also not necessarily true. Even though M1 and M2 accept the same language, it doesn't imply that they have the same halting behavior. M2 may halt on inputs where M1 halts, but it may also halt on additional inputs that are not accepted by M1.
c) On every input which M1 accepts, M2 halts.
This statement is true. Since M1 and M2 accept the same language, if M1 accepts an input, it means that the input belongs to the language. Since M2 also accepts the same language, it must halt on the same input. If M2 didn't halt on an input that M1 accepted, then M2 would not accept the language L(M1) = L(M2), which contradicts the given condition.
d) None of the above.
This option can be eliminated as we have already determined that option 'C' is the correct answer.
Conclusion:
The correct answer is option 'C'. On every input that is accepted by M1, M2 will halt as well. This is because both Turing machines accept the same language. However, the other options are not necessarily true.
Consider the regular expression R = (a + b)* (aa + bb) (a + b)*Which one of the regular expressions given below defines the same language as defined by the regular expression R?- a)(a(ba)* + b(ab)*)(a + b)+
- b)(a(ba)* + b(ab)*)*(a + b)*
- c)(a(ba)* (a + bb) + b(ab)*(b + aa))(a + b)*
- d) (a(ba)* (a + bb) + b(ab)*(b + aa))(a + b)+
Correct answer is option 'C'. Can you explain this answer?
Consider the regular expression R = (a + b)* (aa + bb) (a + b)*
Which one of the regular expressions given below defines the same language as defined by the regular expression R?
a)
(a(ba)* + b(ab)*)(a + b)+
b)
(a(ba)* + b(ab)*)*(a + b)*
c)
(a(ba)* (a + bb) + b(ab)*(b + aa))(a + b)*
d)
(a(ba)* (a + bb) + b(ab)*(b + aa))(a + b)+
|
|
Ravi Singh answered |
R = (a+b)*(aa+bb)(a+b)*
having NFA
Equivalent DFA :
which is equivalent Transition graph [ by removing transition from q1 to q2 and q2 to q1 but does not effect on language ..be careful ]
That is equivalent to
which is equivalent to
which is equivalent to
so equivalent regular expression is [a(ba)*(a+bb) + b(ab)*(b+aa)](a+b)* so option C is answer.
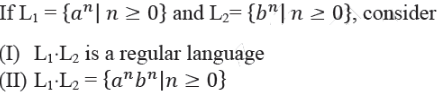Q. Which one of the following is CORRECT?- a)Only (I)
- b)Only (II)
- c)Both (I) and (II)
- d)Neither (I) nor (II)
Correct answer is option 'A'. Can you explain this answer?
Q. Which one of the following is CORRECT?
a)
Only (I)
b)
Only (II)
c)
Both (I) and (II)
d)
Neither (I) nor (II)
|
Pie Academy answered |
L1.L2 is also regular since regular languages are closed under concatenation.
But, L1.L2 is not { anbn | n ≥ 0 }, because both the variable is independent in both languages.
It should have been L1.L2 = { ambn | m ≥ 0, n ≥ 0 }
But, L1.L2 is not { anbn | n ≥ 0 }, because both the variable is independent in both languages.
It should have been L1.L2 = { ambn | m ≥ 0, n ≥ 0 }
Consider a DFA over ∑ = {a, b} accepting all strings which have number of a’s divisible by 6 and number of b’s divisible by 8. What is the minimum number of states that the DFA will have?- a)8
- b)14
- c)15
- d)48
Correct answer is option 'D'. Can you explain this answer?
Consider a DFA over ∑ = {a, b} accepting all strings which have number of a’s divisible by 6 and number of b’s divisible by 8. What is the minimum number of states that the DFA will have?
a)
8
b)
14
c)
15
d)
48
|
|
Ravi Singh answered |
We construct a DFA for strings divisible by 6. It requires minimum 6 states as length of string mod 6 = 0, 1, 2, 3, 4, 5
We construct a DFA for strings divisible by 8. It requires minimum 8 states as length of string mod 8 = 0, 1, 2, 3, 4, 5, 6, 7
If first DFA is minimum and second DFA is also minimum then after merging both DFAs resultant DFA will also be minimum. Such DFA is called as compound automata.
So, minimum states in the resultant DFA = 6 * 8 = 48
Thus, option (D) is the answer.
Please comment below if you find anything wrong in the above post.
We construct a DFA for strings divisible by 8. It requires minimum 8 states as length of string mod 8 = 0, 1, 2, 3, 4, 5, 6, 7
If first DFA is minimum and second DFA is also minimum then after merging both DFAs resultant DFA will also be minimum. Such DFA is called as compound automata.
So, minimum states in the resultant DFA = 6 * 8 = 48
Thus, option (D) is the answer.
Please comment below if you find anything wrong in the above post.
If the regular set A is represented by A — (01 + 1)* and the regular set B is represented by B — ((01)*1*)*, which of the following is true?- a)A ⊂ B
- b)B ⊂ A
- c)A and B are incomparable
- d)A = B
Correct answer is option 'D'. Can you explain this answer?
If the regular set A is represented by A — (01 + 1)* and the regular set B is represented by B — ((01)*1*)*, which of the following is true?
a)
A ⊂ B
b)
B ⊂ A
c)
A and B are incomparable
d)
A = B
|
|
Yash Patel answered |
Both generates all strings over {0,1} where a 0 is immediately followed by a 1.
2Relate the following statement:
Statement: All sufficiently long words in a regular language can have a middle section of words repeated a number of times to produce a new word which also lies within the same language.- a)Turing Machine
- b)Pumping Lemma
- c)Arden’s theorem
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Relate the following statement:
Statement: All sufficiently long words in a regular language can have a middle section of words repeated a number of times to produce a new word which also lies within the same language.
Statement: All sufficiently long words in a regular language can have a middle section of words repeated a number of times to produce a new word which also lies within the same language.
a)
Turing Machine
b)
Pumping Lemma
c)
Arden’s theorem
d)
None of the mentioned
|
Vaibhav Choudhary answered |
B) Pumping Lemma
The statement is related to the Pumping Lemma, which is a fundamental concept in the theory of regular languages. The Pumping Lemma states that for any sufficiently long word in a regular language, there exists a middle section of the word that can be repeated a number of times to produce a new word that also lies within the same language. This lemma is used to prove properties of regular languages and is essential in the study of formal languages and automata theory.
The statement is related to the Pumping Lemma, which is a fundamental concept in the theory of regular languages. The Pumping Lemma states that for any sufficiently long word in a regular language, there exists a middle section of the word that can be repeated a number of times to produce a new word that also lies within the same language. This lemma is used to prove properties of regular languages and is essential in the study of formal languages and automata theory.
Fill in the blank in terms of p, where p is the maximum string length in L. Statement: Finite languages trivially satisfy the pumping lemma by having n = ______- a)p*1
- b)p+1
- c)p-1
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Fill in the blank in terms of p, where p is the maximum string length in L. Statement: Finite languages trivially satisfy the pumping lemma by having n = ______
a)
p*1
b)
p+1
c)
p-1
d)
None of the mentioned
|
|
Sudhir Patel answered |
Finite languages trivially satisfy the pumping lemma by having n equal to the maximum string length in l plus 1.
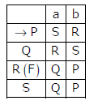
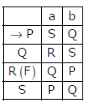
Given below are two finite state automata (→ indicates the start state and F indicates a final state)Which of the following represents the product automaton Z×Y?
- a)
- b)
- c)
- d)
Correct answer is option 'A'. Can you explain this answer?
Given below are two finite state automata (→ indicates the start state and F indicates a final state)Which of the following represents the product automaton Z×Y?
a)
b)
c)
d)
|
Shivam Sharma answered |
All four states 11, 21, 22 , 12 are interpreted as P, Q, R and S. By looking at options we can easily find out that →11 is P and 22(F) is R. Now say 12 is S and 21 is Q.
Let’s construct the transition table for ZxY.
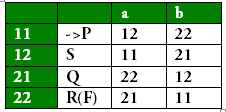
So, the answer should be (A) but in the row for S, it should be P and Q and not Q and P.
Let L1 and L2 be languages over an alphabet £ such that L1 ⊂ L2. Which of the following is true- a)If L2 is regular, then L1 must also be regular.
- b)If L1 is regular, then L2 must also be regular.
- c)Either L1 both and L2 are regular, or both are not regular.
- d)None of the above.
Correct answer is option 'D'. Can you explain this answer?
Let L1 and L2 be languages over an alphabet £ such that L1 ⊂ L2. Which of the following is true
a)
If L
2
is regular, then L1 must also be regular.b)
If L1 is regular, then L2 must also be regular.
c)
Either L1 both and L2 are regular, or both are not regular.
d)
None of the above.
|
|
Raghav Sharma answered |
Contradiction for A. Let L2 = {a,b}* ... which is regular.
And L1 = anbn which is CFL but not regular.
And here L1 is subset of L2.
Contradiction for B. Let L1 = ab ,
which is regular. And L2 = anbn which is CFL but not regular.
And here L1 is subset of L2.
C- > False , ( reason A and B).
Let L be a given context-free language over the alphabet 
. Construct L1 ,L2 as follows. Let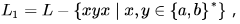 
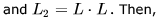
- a)Both L1 and L2 are regular.
- b)Both L1 and L2 are context free but not necessarily regular.
- c)L1 is regular and L2 is context free.
- d)L1 and L2 both may not be context free.
- e)L1 is regular but L2 may not be context free.
Correct answer is option 'C'. Can you explain this answer?
Let L be a given context-free language over the alphabet . Construct L1 ,L2 as follows. Let
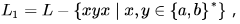
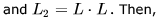
. Construct L1 ,L2 as follows. Let a)
Both L1 and L2 are regular.
b)
Both L1 and L2 are context free but not necessarily regular.
c)
L1 is regular and L2 is context free.
d)
L1 and L2 both may not be context free.
e)
L1 is regular but L2 may not be context free.
|
|
Rhea Reddy answered |
L2 = L.L
Context free languages are closed under Concatenation.
So L2 is Context Free Language.
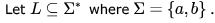Which of the following is true?- a)
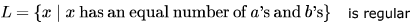
- b)
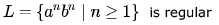
- c)
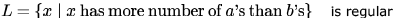
- d)
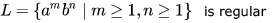
Correct answer is option 'D'. Can you explain this answer?
Which of the following is true?a)
b)
c)
d)
|
|
Ravi Singh answered |
Only D. because n and m are independent and thus no memory element required. a and b are same and are DCFL's.
c is L = { an bm | n > m }. which is not regular.
Correction:I think c should be that x has more a's than b's.
Correction:I think c should be that x has more a's than b's.
Consider the regular grammar below
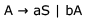The Myhill-Nerode equivalence classes for the language generated by the grammar are- a)
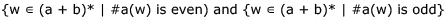
- b)
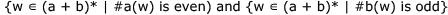
- c)
- d)
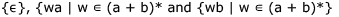
Correct answer is option 'A'. Can you explain this answer?
Consider the regular grammar below
The Myhill-Nerode equivalence classes for the language generated by the grammar are
a)
b)
c)
d)
|
|
Avinash Sharma answered |
The given grammar generates all string over the alphabet {a,b} which have an even number of 's.
The given right-linear grammar can be converted to the following DFA.
The given right-linear grammar can be converted to the following DFA.
Can you explain the answer of this question below:Consider the languages L1 = 
and L2 = {a}. Which one of the following represents L1 L2* U L1*
- A:A
- B:B
- C:C
- D:D
The answer is a.
Consider the languages L1 = and L2 = {a}. Which one of the following represents L1 L2* U L1*
and L2 = {a}. Which one of the following represents L1 L2* U L1*A:
A
B:
B
C:
C
D:
D
|
|
Ankita Chopra answered |
Since L1 is empty.The concatenation of any other language with empty language is always empty.Hence L1 L2* evaluates to be empty language. Hence , L1 L2* = {Φ} . a* = {Φ} The kleene closure of empty language always gives null string hence Φ* = {∈} Final answer evaluates to be {Φ} U {∈} = {∈}.
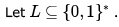Which of the following is true?- a)If L is regular, all subsets of L are regular.
- b)If all proper subsets of L are regular, then L is regular.
- c)If all finite subsets of L are regular, then L is regular.
- d)If a proper subset of L is not regular, then L is not regular.
Correct answer is option 'C'. Can you explain this answer?
Which of the following is true?a)
If L is regular, all subsets of L are regular.
b)
If all proper subsets of L are regular, then L is regular.
c)
If all finite subsets of L are regular, then L is regular.
d)
If a proper subset of L is not regular, then L is not regular.
|
|
Yash Patel answered |
Ans C) Every finite subset should always be regular
A set may be regular
It's all subset is not regular all the time
Say (0+1)* is regular but 0n1n is not regular
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only.Let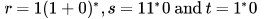 
be three regular expressions. Which one of the following is true?- a)
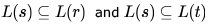
- b)
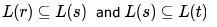
- c)
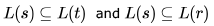
- d)
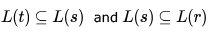
- e)None of the above
Correct answer is option 'A,C'. Can you explain this answer?
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only.
Let 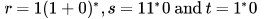be three regular expressions. Which one of the following is true?
be three regular expressions. Which one of the following is true?a)
b)
c)
d)
e)
None of the above
|
Zoya Sharma answered |
to know the ans let us check all the options.
strings generated by S are any numbers of 1's followed by one 0, i.e., 10,110,1110,1110,......) Strings generated by r are is 1 followed by any combination of 0 or 1, i.e., 1,10,11,1110,101,110,.....This shows that all the strings that can be generated by S,can also be generated by r it means 
here strings generated by t are any numbers of 1 (here 1* means we have strings as 
followed by only one 0, i.e., 0,10,110,1110,.....So we can see that all the strings that are present in S can also begenerated by t, hence
which shows that option A is true.
this is false because string 1 which can be generated by r, cannot be generated by SSame as option A.
. this is false because string 0 which can be generated by t ,cannot be generated by S .In the context-free grammar below, S is the start symbol, a and b are terminals, and ϵ denotes the empty string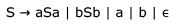
Which of the following strings is NOT generated by the grammar?- a)aaaa
- b)baba
- c)abba
- d)babaaabab
Correct answer is option 'B'. Can you explain this answer?
In the context-free grammar below, S is the start symbol, a and b are terminals, and ϵ denotes the empty string
Which of the following strings is NOT generated by the grammar?
a)
aaaa
b)
baba
c)
abba
d)
babaaabab
|
Sagar Kumar answered |
This grammar generates strings having start symbol and end symbol same and in option (B) start symbol is 'b' and end symbol is 'a'.
So option (b) is not true.
So option (b) is not true.
Let denote the languages generated by the grammar S→ 0S0 I 00.Which of the following is TRUE?- a)L=0+
- b)L is regular but not 0+
- c) L is context free but not regular
- d)L is not context free
Correct answer is option 'B'. Can you explain this answer?
Let denote the languages generated by the grammar S→ 0S0 I 00.
Which of the following is TRUE?
a)
L=0+
b)
L is regular but not 0+
c)
L is context free but not regular
d)
L is not context free
|
|
Aditya Deshmukh answered |
Option A : L is not 0+ , because 0+ will contain any arbitrary string over alphabet 0 with any no of 0’s ( except empty string ), for ex: {0, 00, 000,00000}, but L will only have the strings as { 00, 0000, 000000,…}, i.e only even no of 0’s ( excluding empty string}.
Option D : L is a Context Free Language, because the Grammar G which generates the language L is Context Free Grammar. A Grammar G is CFG if all of its productions are of the form A->α, where A is a single non-terminal and α belongs to (V∪ T)* , i.e α can be a string of terminals and/or Non-terminals. (V represents a non-terminal and T represents a terminal)
Option C : L is a Regular Language, Because we are able to write a regular expression for it ( and also able to make a Finite Automaton), which is (00)+.
Option B : Hence This option is Correct, because L is Regular but not 0+, as we proved above.
Which of the following statements is TRUE about the regular expression 01*0?- a)It represents a finite set of finite strings.
- b)It represents an infinite set of finite strings.
- c)It represents a finite set of infinite strings.
- d)It represents an infinite set of infinite strings.
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is TRUE about the regular expression 01*0?
a)
It represents a finite set of finite strings.
b)
It represents an infinite set of finite strings.
c)
It represents a finite set of infinite strings.
d)
It represents an infinite set of infinite strings.
|
|
Ravi Singh answered |
Infinite set (because of *) of finite strings. A string is defined as a FINITE sequence of characters and hence can never be infinite.
Which one of the following regular expressions is NOT equivalent to the regular expression (a + b + c)*?- a)(a* + b* + c*)*
- b)(a*b*c*)*
- c)((ab)* + c*)*
- d)(a*b* + c*)*
Correct answer is option 'C'. Can you explain this answer?
Which one of the following regular expressions is NOT equivalent to the regular expression (a + b + c)*?
a)
(a* + b* + c*)*
b)
(a*b*c*)*
c)
((ab)* + c*)*
d)
(a*b* + c*)*
|
|
Ravi Singh answered |
A) (a* + b* + c*)* = ( ^ + a+aa+.. ..+b+bb+...+c+cc...)* = (a+b+c+ aa+..+bb+..+cc+..)*= (a+b+c)* [any combination of rest of aa ,bb,cc, etc already come in (a+b+c)* ]
(a*b*c*)* = (a*+b*+c* +a*b*+b*c*+a*c*+..)*= (a+b+c+....)* = (a+b+c)*
((ab)* + c*)* =(ab+c+^+abab+...)* = (ab+c)*
(a*b* + c*)* = (a*+b*+c*+...)* =(a+b+c+..)* = (a+b+c)*
Given the language L = {ab, aa, baa}, which of the following strings are in L*?1) abaabaaabaa
2) aaaabaaaa
3) baaaaabaaaab
4) baaaaabaa- a)1, 2 and 3
- b)2, 3 and 4
- c)1, 2 and 4
- d)1, 3 and 4
Correct answer is 'C'. Can you explain this answer?
Given the language L = {ab, aa, baa}, which of the following strings are in L*?
1) abaabaaabaa
2) aaaabaaaa
3) baaaaabaaaab
4) baaaaabaa
2) aaaabaaaa
3) baaaaabaaaab
4) baaaaabaa
a)
1, 2 and 3
b)
2, 3 and 4
c)
1, 2 and 4
d)
1, 3 and 4
|
|
Shivam Sharma answered |
The answer is c.Any combination of strings in set {ab, aa, baa} will be in L*.….1) “abaabaaabaa” can be partitioned as a combination of strings in set {ab, aa, baa}. The partitions are “ab aa baa ab aa”….2) “aaaabaaaa” can be partitioned as a combination of strings in set {ab, aa, baa}. The partitions are “aa ab aa aa”….3) “baaaaabaaaab” cannot be partitioned as a combination of strings in set {ab, aa, baa}….4) “baaaaabaa” can be partitioned as a combination of strings in set {ab, aa, baa}. The partitions are “baa aa ab aa”
What can be said about a regular language L over { a } whose minimal finite state automaton has two states?- a)L must be {an | n is odd}
- b)L must be {an | n is even}
- c)L must be {an | n ≥ 0}
- d)Either L must be {a. | n is odd}, or L must be {an | n is even}
Correct answer is option 'D'. Can you explain this answer?
What can be said about a regular language L over { a } whose minimal finite state automaton has two states?
a)
L must be {an | n is odd}
b)
L must be {an | n is even}
c)
L must be {an | n ≥ 0}
d)
Either L must be {a. | n is odd}, or L must be {an | n is even}
|
|
Ravi Singh answered |
Because if we draw the minimal dfa for each of them, we will get two states each.
Whereas, {an| n>=0} requires only one state.
Whereas, {an| n>=0} requires only one state.
Which of the following statements is TRUE about the regular expression 01*0?- a)It represents a finite set of finite strings.
- b)It represents an infinite set of finite strings.
- c)It represents a finite set of infinite strings.
- d)It represents an infinite set of infinite strings
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is TRUE about the regular expression 01*0?
a)
It represents a finite set of finite strings.
b)
It represents an infinite set of finite strings.
c)
It represents a finite set of infinite strings.
d)
It represents an infinite set of infinite strings
|
|
Atharva Kulkarni answered |
Regular Expression 01*0?
- Regular Expression: A regular expression is a sequence of characters that specifies a search pattern.
- 01*0?: The given regular expression represents a string that starts with 0 followed by zero or more occurrences of 1 and ends with an optional 0.
Finite or Infinite?
- A set of strings is said to be finite if it has a finite number of elements.
- A set of strings is said to be infinite if it has an infinite number of elements.
The regular expression 01*0? represents an infinite set of finite strings.
Explanation:
- The regular expression starts with 0, which means the first character of every string in this set is fixed and finite.
- The regular expression allows zero or more occurrences of 1 after the first character. This means that the number of 1's in the string can be any non-negative integer, which makes the set of strings infinite.
- The regular expression ends with an optional 0. This means that the last character of every string can either be 0 or absent, which makes the set of strings infinite.
Conclusion:
- The regular expression 01*0? represents an infinite set of finite strings.
- It starts with a fixed character and allows a variable number of occurrences of another character, which makes the set of strings infinite.
- Regular Expression: A regular expression is a sequence of characters that specifies a search pattern.
- 01*0?: The given regular expression represents a string that starts with 0 followed by zero or more occurrences of 1 and ends with an optional 0.
Finite or Infinite?
- A set of strings is said to be finite if it has a finite number of elements.
- A set of strings is said to be infinite if it has an infinite number of elements.
The regular expression 01*0? represents an infinite set of finite strings.
Explanation:
- The regular expression starts with 0, which means the first character of every string in this set is fixed and finite.
- The regular expression allows zero or more occurrences of 1 after the first character. This means that the number of 1's in the string can be any non-negative integer, which makes the set of strings infinite.
- The regular expression ends with an optional 0. This means that the last character of every string can either be 0 or absent, which makes the set of strings infinite.
Conclusion:
- The regular expression 01*0? represents an infinite set of finite strings.
- It starts with a fixed character and allows a variable number of occurrences of another character, which makes the set of strings infinite.
The string 1101 does not belong to the set represented by- a)110*(0 + 1)
- b)1(0 + 1)*101
- c)(10)*(01)*(00 + 11)*
- d)(00 + (11)*0)*
Correct answer is option 'A,B'. Can you explain this answer?
The string 1101 does not belong to the set represented by
a)
110*(0 + 1)
b)
1(0 + 1)*101
c)
(10)*(01)*(00 + 11)*
d)
(00 + (11)*0)*
|
|
Rajeev Sharma answered |
R.E of option C won’t generate 1101 as you can see the language will contain L(C) = {epsilon,10,1010,1001,0101,00,11,0011,1100,………..}
Also, R.E of option D has ‘1’ but here two ’11’ are together hence its impossible to generate 1101.L(D) = {Epsilon,0,00,110,11110,11000,…………….}
Here Option (C) and (D) both are correct.
Which one of the following languages over the alphabet {0,1} is described by the regular expression: (0+1)*0(0+1)*0(0+1)*?- a)The set of all strings containing the substring 00.
- b)The set of all strings containing at most two 0’s.
- c)The set of all strings containing at least two 0’s.
- d)The set of all strings that begin and end with either 0 or 1.
Correct answer is option 'C'. Can you explain this answer?
Which one of the following languages over the alphabet {0,1} is described by the regular expression: (0+1)*0(0+1)*0(0+1)*?
a)
The set of all strings containing the substring 00.
b)
The set of all strings containing at most two 0’s.
c)
The set of all strings containing at least two 0’s.
d)
The set of all strings that begin and end with either 0 or 1.
|
|
Anisha Chavan answered |
The regular expression has two 0′s surrounded by (0+1)* which means accepted strings must have at least 2 0′s.
Consider the alphabet ∑ = {0,1} , the null/empty string λ and the set of strings X0,X1 and X2 generated by the corresponding non-terminals of a regular grammar. X0,X1 and X2 are related as follows.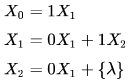
Which one of the following choices precisely represents the strings in X0?- a)10(0*+(10)*)1
- b)10(0*+(10)*)*1
- c)1(0+10)*1
- d)10(0+10)*1 +110(0+10)*1
Correct answer is option 'C'. Can you explain this answer?
Consider the alphabet ∑ = {0,1} , the null/empty string λ and the set of strings X0,X1 and X2 generated by the corresponding non-terminals of a regular grammar. X0,X1 and X2 are related as follows.
Which one of the following choices precisely represents the strings in X0?
a)
10(0*+(10)*)1
b)
10(0*+(10)*)*1
c)
1(0+10)*1
d)
10(0+10)*1 +110(0+10)*1
|
|
Sanya Agarwal answered |
Here we have little different version of Arden's Theorem
if we have R= PR + Q then it has a solution R = P*Q
Proof : R= PR+ Q
= P(PR+Q)+Q (by putting R= PR+Q)
= P(PR+Q)+Q (by putting R= PR+Q)
= PPR+PQ+Q
=PP(PR+Q)+PQ+Q (by putting R= PR+Q)
= PPPR+PPQ+PQ+Q
and so on , we get R
= {..........+PPPPQ+PPPQ+PPQ+PQ+Q} = {..........+PPPP+PPP+PP+P+ ^}Q = P*Q
or Another way R=PR+Q
= P(P*Q) + Q (by putting R = P*Q)
=(PP* + ^)Q = P*Q
So Equation is Proved .
Now for the Above Question
X1= 0X1 + 1 X2 (Equation 2)
= 0X1 +1(0X1 + ^) ( Put the value of X2 from Equation 3 )
=0X1 +10 X1+ 1 = (0+10)X1 +1
X1= (0+10)*1 (Apply if R = PR + Q then R = P*Q)
X0 = 1 X1 ( Equation 1)
X0 = 1(0+10)*1 ( Put the value of X1 we calculated).
So 1(0+10)*1 option C is correct.
So 1(0+10)*1 option C is correct.
Chapter doubts & questions for Theory of Computation - GATE Computer Science Engineering(CSE) 2026 Mock Test Series 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Theory of Computation - GATE Computer Science Engineering(CSE) 2026 Mock Test Series in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup