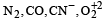All Exams >
NEET >
Chemistry 31 Years NEET Chapterwise Solved Papers >
All Questions
All questions of Structure of Atom for NEET Exam
The maximum number of electrons in a subshell is given by the expression [1989]- a)4l – 2
- b)4l + 2
- c)2l + 2
- d)2n2
Correct answer is option 'B'. Can you explain this answer?
The maximum number of electrons in a subshell is given by the expression [1989]
a)
4l – 2
b)
4l + 2
c)
2l + 2
d)
2n2
|
Akshat Chavan answered |
No. of orbitals in a sub-shell = 2 ℓ + 1
⇒ No. of electrons = 2(2ℓ + 1) = 4ℓ + 2
The spectrum of He is expected to be similar to that[1988]- a)H
- b)Li+
- c)Na
- d)He+
Correct answer is option 'B'. Can you explain this answer?
The spectrum of He is expected to be similar to that[1988]
a)
H
b)
Li+
c)
Na
d)
He+
|
Arindam Khanna answered |
Both He and Li+ contain 2 electrons each therefore their spectrum will be similar.
The frequency of radiation emitted when the electron falls from n = 4 to n = 1 in a hydrogen atom will be (Given ionization energy of H=2.18 ×10–18J atom–1and h = 6.625 × 10–34 J s ) [2004]- a)1.54 x 1015 s -1
- b)1.03 x 1015 s -1
- c)3.08 x 1015 s -1
- d)2.00 x 1015 s -1
Correct answer is option 'C'. Can you explain this answer?
The frequency of radiation emitted when the electron falls from n = 4 to n = 1 in a hydrogen atom will be (Given ionization energy of H=2.18 ×10–18J atom–1and h = 6.625 × 10–34 J s ) [2004]
a)
1.54 x 1015 s -1
b)
1.03 x 1015 s -1
c)
3.08 x 1015 s -1
d)
2.00 x 1015 s -1
|
Harshitha Dey answered |
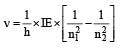
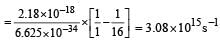
If n = 6, the correct sequence for filling of electrons will be : [2011]- a)ns →(n – 2) f → (n – 1) d → np
- b)ns →(n – 1) d → (n – 2) f → np
- c)ns →(n – 2) f → np →(n – 1) d
- d)ns → np (n – 1) d →(n – 2) f
Correct answer is option 'A'. Can you explain this answer?
If n = 6, the correct sequence for filling of electrons will be : [2011]
a)
ns →(n – 2) f → (n – 1) d → np
b)
ns →(n – 1) d → (n – 2) f → np
c)
ns →(n – 2) f → np →(n – 1) d
d)
ns → np (n – 1) d →(n – 2) f
|
Krish Saha answered |
ns → (n - 2)f → (n - 1)d → np [n = 6]
Which of the following is isoelectronic? [2002]- a)CO2, NO2
- b)NO2–, CO2
- c)CN–, CO
- d)SO2, CO2
Correct answer is option 'C'. Can you explain this answer?
Which of the following is isoelectronic? [2002]
a)
CO2, NO2
b)
NO2–, CO2
c)
CN–, CO
d)
SO2, CO2
|
Dipanjan Chawla answered |
Both CN– and CO have 14 electrons
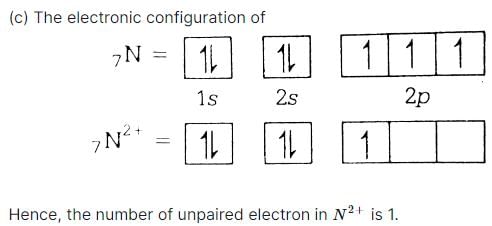
The electronic configuration for oxygen is written as 1s22s22p4. Which rule will this configuration be violating?- a)Aufbau’s principle.
- b)Hund’s rule.
- c)Pauli’s exclusion principle.
- d)None of the above.
Correct answer is option 'D'. Can you explain this answer?
The electronic configuration for oxygen is written as 1s22s22p4. Which rule will this configuration be violating?
a)
Aufbau’s principle.
b)
Hund’s rule.
c)
Pauli’s exclusion principle.
d)
None of the above.
|
Arpita Choudhury answered |
B)Hund's rule
c)Pauli exclusion principle
d)None of the above
Answer: a) Aufbau rule
c)Pauli exclusion principle
d)None of the above
Answer: a) Aufbau rule
Maximum number of electrons in a subshell of an atom is determined by the following:- a)2l + 1
- b)4l – 2 [2009]
- c)2n2
- d)4l + 2
Correct answer is option 'D'. Can you explain this answer?
Maximum number of electrons in a subshell of an atom is determined by the following:
a)
2l + 1
b)
4l – 2 [2009]
c)
2n2
d)
4l + 2
|
Shounak Nair answered |
The number of sub shell is (2 l + 1). The maximum number of electrons in the sub shell is 2 (2 l + 1) = (4 l + 2)
For azimuthal quantum number ℓ = 3, the maximum number of electrons will be [1991]- a)2
- b)6
- c)0
- d)14.
Correct answer is option 'D'. Can you explain this answer?
For azimuthal quantum number ℓ = 3, the maximum number of electrons will be [1991]
a)
2
b)
6
c)
0
d)
14.
|
Naveen Menon answered |
ℓ = 3 means f-subshell. Maximum no. of electrons = 4ℓ + 2 = 4 × 3 + 2 = 14
Maximum number of electrons in a subshell with : l = 3 and n = 4 is : [2012]- a)14
- b)16
- c)10
- d)12
Correct answer is option 'A'. Can you explain this answer?
Maximum number of electrons in a subshell with : l = 3 and n = 4 is : [2012]
a)
14
b)
16
c)
10
d)
12
|
Pooja Saha answered |
(n = 4, l = 3) ⇒ 4f subshell Since, maximum no. of electrons in a subshell = 2(2l + 1)
So, total no. of electron in 4f subshell = 2 (2 × 3 + 1) = 14 electrons.
So, total no. of electron in 4f subshell = 2 (2 × 3 + 1) = 14 electrons.
Which one of the following species does not exist under normal conditions? [2010]- a)Be2+
- b)Be2
- c)B2
- d)Li2
Correct answer is option 'B'. Can you explain this answer?
Which one of the following species does not exist under normal conditions? [2010]
a)
Be2+
b)
Be2
c)
B2
d)
Li2
|
Maheshwar Saini answered |
Bond order of Be2 = 0, hence Be2 cannot exist.
The orientation of an atomic orbital is governed by [2006]- a)Spin quantum number
- b)Magnetic quantum number
- c)Principal quantum number
- d)Azimuthal quantum number
Correct answer is option 'B'. Can you explain this answer?
The orientation of an atomic orbital is governed by [2006]
a)
Spin quantum number
b)
Magnetic quantum number
c)
Principal quantum number
d)
Azimuthal quantum number
|
Rhea Sarkar answered |
Magnetic quantum no. represents the orientation of atomic orbitals in an atom. For example px, py & pz have orientation along X-axis, Y-axis & Z-axis
According to Bohr ’s theory the energy required for an electron in the Li2+ ion to be emitted from n = 2 state is (given that the ground state ionization energy of hydrogen atom is 13.6 eV)- a)61.2 eV
- b)13.6 eV [1999]
- c)30.6 eV
- d)10.2 eV
Correct answer is option 'C'. Can you explain this answer?
According to Bohr ’s theory the energy required for an electron in the Li2+ ion to be emitted from n = 2 state is (given that the ground state ionization energy of hydrogen atom is 13.6 eV)
a)
61.2 eV
b)
13.6 eV [1999]
c)
30.6 eV
d)
10.2 eV
|
|
Krish Saha answered |
Energy of electron in 2nd or bit of Li+2
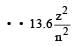
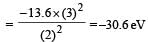
Energy required = 0 – (–30.6) = 30.6 eV
If r is the radius of the first orbit, the radius of nth orbit of H-atom is given by [1988]
- a)rn2
- b)rn
- c)r/n
- d)r2 n2
Correct answer is option 'A'. Can you explain this answer?
If r is the radius of the first orbit, the radius of nth orbit of H-atom is given by [1988]
a)
rn2
b)
rn
c)
r/n
d)
r2 n2
|
Moumita Khanna answered |
According to Bohr's Model:
r ∝n2/Z
So, radius of nth orbit is rn=rn2, as Z=1 for H atom.
r ∝n2/Z
So, radius of nth orbit is rn=rn2, as Z=1 for H atom.
The ion that is isoelectronic with CO is [1997]- a)CN–
- b)O2+
- c)O2–
- d)N2+
Correct answer is option 'A'. Can you explain this answer?
The ion that is isoelectronic with CO is [1997]
a)
CN–
b)
O2+
c)
O2–
d)
N2+
|
|
Moumita Khanna answered |
We know that ions which have th e same number of electrons are called isoelectronic.
We also know that both CO and CN– have 14 electrons, therefore these are isoelectronic.
We also know that both CO and CN– have 14 electrons, therefore these are isoelectronic.
Given : The mass of electron is 9.11 × 10–31 kg Plank constant is 6.626 × 10–34 Js, the uncertainty involved in the measurement of velocity within a distance of 0.1 Å is [2006]- a)5.79 × 107 ms–1
- b)5.79 × 108 ms–1
- c)5.79 × 105 ms–1
- d)5.79 × 106 ms–1
Correct answer is option 'D'. Can you explain this answer?
Given : The mass of electron is 9.11 × 10–31 kg Plank constant is 6.626 × 10–34 Js, the uncertainty involved in the measurement of velocity within a distance of 0.1 Å is [2006]
a)
5.79 × 107 ms–1
b)
5.79 × 108 ms–1
c)
5.79 × 105 ms–1
d)
5.79 × 106 ms–1
|
Jananignanamurugan Janan answered |
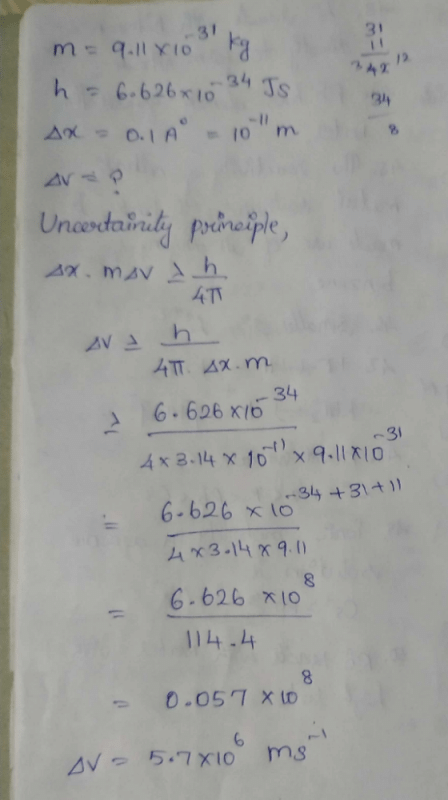
The energy of the second Bohr orbit of the hydrogen atom is -328 kJ mol-1; hence the energy of the fourth Bohr orbit would be: [2005]- a)-41 kJ mol-1
- b)-82 kJ mol-1
- c)-164 kJ mol-1
- d)-1312 kJ mol-1
Correct answer is option 'B'. Can you explain this answer?
The energy of the second Bohr orbit of the hydrogen atom is -328 kJ mol-1; hence the energy of the fourth Bohr orbit would be: [2005]
a)
-41 kJ mol-1
b)
-82 kJ mol-1
c)
-164 kJ mol-1
d)
-1312 kJ mol-1
|
Rohan Nambiar answered |
Explanation:
The energy of an electron in the nth orbit of a hydrogen atom is given by the formula:
E = -13.6/n^2 eV
Where E is the energy in electron volts and n is the principal quantum number.
To convert the energy from electron volts to kilojoules per mole, we can use the conversion factor:
1 eV = 96.485 kJ/mol
Step 1:
First, let's convert the given energy of the second Bohr orbit from kJ/mol to eV.
-328 kJ/mol * (1 eV / 96.485 kJ/mol) = -3.396 eV
Step 2:
Now, we can use the formula above to find the energy of the fourth Bohr orbit.
E = -13.6/n^2 eV
E = -13.6/4^2 eV
E = -13.6/16 eV
E = -0.85 eV
Step 3:
Finally, let's convert the energy of the fourth Bohr orbit from eV to kJ/mol.
-0.85 eV * (96.485 kJ/mol / 1 eV) = -82.12 kJ/mol
Therefore, the energy of the fourth Bohr orbit of the hydrogen atom is approximately -82 kJ/mol, which corresponds to option B.
The energy of an electron in the nth orbit of a hydrogen atom is given by the formula:
E = -13.6/n^2 eV
Where E is the energy in electron volts and n is the principal quantum number.
To convert the energy from electron volts to kilojoules per mole, we can use the conversion factor:
1 eV = 96.485 kJ/mol
Step 1:
First, let's convert the given energy of the second Bohr orbit from kJ/mol to eV.
-328 kJ/mol * (1 eV / 96.485 kJ/mol) = -3.396 eV
Step 2:
Now, we can use the formula above to find the energy of the fourth Bohr orbit.
E = -13.6/n^2 eV
E = -13.6/4^2 eV
E = -13.6/16 eV
E = -0.85 eV
Step 3:
Finally, let's convert the energy of the fourth Bohr orbit from eV to kJ/mol.
-0.85 eV * (96.485 kJ/mol / 1 eV) = -82.12 kJ/mol
Therefore, the energy of the fourth Bohr orbit of the hydrogen atom is approximately -82 kJ/mol, which corresponds to option B.
Which of the following statements do not form a part of Bohr ’s model of hydrogen atom ? [1989]- a)Energy of the electron s in the or bits are quantized
- b)The electron in the orbit nearest the nucleus has the lowest energy
- c)Electrons revolve in different orbits around the nucleus
- d)The position and velocity of the electrons in the orbit cannot be determined simultaneously.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements do not form a part of Bohr ’s model of hydrogen atom ? [1989]
a)
Energy of the electron s in the or bits are quantized
b)
The electron in the orbit nearest the nucleus has the lowest energy
c)
Electrons revolve in different orbits around the nucleus
d)
The position and velocity of the electrons in the orbit cannot be determined simultaneously.
|
|
Shounak Nair answered |
is uncertainty principle which was given by Hiesenberg and not Bohr’s postulate
Consider the following sets of quantum numbers: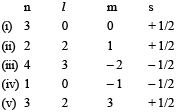
Which of the following sets of quantum number is not possible? [2007]- a)(i), (ii), (iii) and (iv)
- b)(ii), (iv) and (v)
- c)(i) and (iii)
- d)(ii), (iii) and (iv)
Correct answer is option 'B'. Can you explain this answer?
Consider the following sets of quantum numbers:
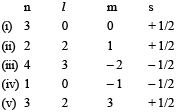
Which of the following sets of quantum number is not possible? [2007]
a)
(i), (ii), (iii) and (iv)
b)
(ii), (iv) and (v)
c)
(i) and (iii)
d)
(ii), (iii) and (iv)
|
|
Arindam Khanna answered |
(ii) is not possible for any value of n because l varies from 0 to (n – 1) thus for n = 2, l can be only 0, 1, 2. (iv) is not possible because for l = 0, m = 0. (v) is not possible because for l = 2, m varies from –2 to +2.
Uncertainty in position of an electron (mass = 9.1 × 10–28 g) moving with a velocity of 3 × 104 cm/s accurate upto 0.001% will be (use h/4π) in uncertainty expression where h = 6.626 ×10–27 erg-second) [1995]- a)1.93 cm
- b)3.84 cm
- c)5.76 cm
- d)7.68 cm
Correct answer is option 'A'. Can you explain this answer?
Uncertainty in position of an electron (mass = 9.1 × 10–28 g) moving with a velocity of 3 × 104 cm/s accurate upto 0.001% will be (use h/4π) in uncertainty expression where h = 6.626 ×10–27 erg-second) [1995]
a)
1.93 cm
b)
3.84 cm
c)
5.76 cm
d)
7.68 cm
|
Pranav Datta answered |
1. **Given data**
- Mass of electron (m) = 9.1 × 10^(-28) g
- Velocity of electron (v) = 3 × 10^4 cm/s
- Accuracy = 0.001%
- Planck's constant (h) = 6.626 × 10^(-27) erg-second
2. **Calculating uncertainty in position**
The uncertainty in position (∆x) can be calculated using the formula:
∆x = h / (4π * m * ∆v)
Where:
- h = Planck's constant
- m = mass of the electron
- ∆v = uncertainty in velocity
3. **Calculating uncertainty in velocity**
Uncertainty in velocity can be calculated as a percentage of the actual velocity:
∆v = (0.001/100) * v
∆v = 0.001 * 3 × 10^4
∆v = 30 cm/s
4. **Substitute values in the formula**
∆x = (6.626 × 10^(-27)) / (4π * 9.1 × 10^(-28) * 30)
∆x = 1.93 cm
5. Therefore, the uncertainty in the position of the electron moving with a velocity accurate up to 0.001% is 1.93 cm. Hence, option **A** is correct.
- Mass of electron (m) = 9.1 × 10^(-28) g
- Velocity of electron (v) = 3 × 10^4 cm/s
- Accuracy = 0.001%
- Planck's constant (h) = 6.626 × 10^(-27) erg-second
2. **Calculating uncertainty in position**
The uncertainty in position (∆x) can be calculated using the formula:
∆x = h / (4π * m * ∆v)
Where:
- h = Planck's constant
- m = mass of the electron
- ∆v = uncertainty in velocity
3. **Calculating uncertainty in velocity**
Uncertainty in velocity can be calculated as a percentage of the actual velocity:
∆v = (0.001/100) * v
∆v = 0.001 * 3 × 10^4
∆v = 30 cm/s
4. **Substitute values in the formula**
∆x = (6.626 × 10^(-27)) / (4π * 9.1 × 10^(-28) * 30)
∆x = 1.93 cm
5. Therefore, the uncertainty in the position of the electron moving with a velocity accurate up to 0.001% is 1.93 cm. Hence, option **A** is correct.
The ions O2–, F–, Na+, Mg2+ and Al3+ are isoelectronic. Their ionic radii show [2003]- a)A decrease from O2– to F– and then increase from Na+ to Al3+
- b)A significant increase from O2– to Al3+
- c)A significant decrease from O2– to Al3+
- d)An increase from O2– to F– and then decrease from Na+ to Al3+
Correct answer is option 'C'. Can you explain this answer?
The ions O2–, F–, Na+, Mg2+ and Al3+ are isoelectronic. Their ionic radii show [2003]
a)
A decrease from O2– to F– and then increase from Na+ to Al3+
b)
A significant increase from O2– to Al3+
c)
A significant decrease from O2– to Al3+
d)
An increase from O2– to F– and then decrease from Na+ to Al3+
|
|
Dipanjan Chawla answered |
Amongst isoelectronic species, ionic radii of anion is more than that of cations. Further size of anion increase with increase in-ve change and size of cation decrease with increase in + ve charge. Hence ionic radii decreases from O– to Al+++.
The measurement of the electron position if associated with an uncertainty in momentum, which is equal to 1 × 10–18 g cm s– 1 . The uncertainty in electron velocity is, [2008] (mass of an electron is 9 × 10– 28 g)- a)1 × 109 cm s–1
- b)1 × 106 cm s–1
- c)1 × 105 cm s–1
- d)1 × 1011 cm s–1
Correct answer is option 'A'. Can you explain this answer?
The measurement of the electron position if associated with an uncertainty in momentum, which is equal to 1 × 10–18 g cm s– 1 . The uncertainty in electron velocity is, [2008] (mass of an electron is 9 × 10– 28 g)
a)
1 × 109 cm s–1
b)
1 × 106 cm s–1
c)
1 × 105 cm s–1
d)
1 × 1011 cm s–1
|
|
Satakshi Kumari answered |
∆p=m∆v
∆v=∆p/m
=1×10-18/9×10-28
=1×10 9cm s-1
∆v=∆p/m
=1×10-18/9×10-28
=1×10 9cm s-1
The electron was shown experimentally to have wave properties by [1994]- a)de Broglie
- b)Davisson and Germer
- c)N. Bohr
- d)Schrodinger.
Correct answer is option 'B'. Can you explain this answer?
The electron was shown experimentally to have wave properties by [1994]
a)
de Broglie
b)
Davisson and Germer
c)
N. Bohr
d)
Schrodinger.
|
Pankaj Kulkarni answered |
Wave nature of electr on was shown by Davisson and Germer. Davission and germer demonstrated the physical reality of the wave nature of electrons by showing that a beam of electrons could also diffracted by crystals just like light of x-rays.
What is the maximum numbers of electrons that can be associated with the following set of quantum numbers? n = 3, l = 1 and m = –1 [NEET 2013]- a)6
- b)4
- c)2
- d)10
Correct answer is option 'C'. Can you explain this answer?
What is the maximum numbers of electrons that can be associated with the following set of quantum numbers? n = 3, l = 1 and m = –1 [NEET 2013]
a)
6
b)
4
c)
2
d)
10
|
Aman Sharma answered |
n = 3 → 3rd shell
l = 1 → p sub shell.
m = – 1 is possible for two electrons present in an orbital.
l = 1 → p sub shell.
m = – 1 is possible for two electrons present in an orbital.
The momentum of a particle having a de Broglie wavelength of 10–17 metres is [1996] (Given h = 6.625 × 10–34 Js)- a)3.3125 × 10–7 kg ms–1
- b)26.5 × 10–7 kg ms–1
- c)6.625 × 10–17 kg ms–1
- d)13.25 × 10–17 kg ms–1
Correct answer is option 'C'. Can you explain this answer?
The momentum of a particle having a de Broglie wavelength of 10–17 metres is [1996] (Given h = 6.625 × 10–34 Js)
a)
3.3125 × 10–7 kg ms–1
b)
26.5 × 10–7 kg ms–1
c)
6.625 × 10–17 kg ms–1
d)
13.25 × 10–17 kg ms–1
|
Rajeev Sharma answered |
Acc. to deBroglie
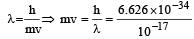.⇒ p = 6.626 × 10–17 kg m/s
When an electron of charge e and mass m moves with a velocity v about the nuclear charge Ze is circular orbit of radius r, the potential energy of the electrons is given by [1994]- a)Ze2/r
- b)-Ze2/r
- c)Ze-2/r
- d)mv2/r
Correct answer is option 'B'. Can you explain this answer?
When an electron of charge e and mass m moves with a velocity v about the nuclear charge Ze is circular orbit of radius r, the potential energy of the electrons is given by [1994]
a)
Ze2/r
b)
-Ze2/r
c)
Ze-2/r
d)
mv2/r
|
|
Naveen Menon answered |
P.E. = work done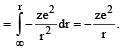 
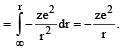
The correct set of four quantum numbers for the valence electron of rubidium atom (Z = 37) is [2012]- a)5, 1, + 1/2
- b)6, 0, 0 + 1/2
- c)5, 0, 0 + 1/2
- d)5, 1, 0 + 1/2
Correct answer is option 'C'. Can you explain this answer?
The correct set of four quantum numbers for the valence electron of rubidium atom (Z = 37) is [2012]
a)
5, 1, + 1/2
b)
6, 0, 0 + 1/2
c)
5, 0, 0 + 1/2
d)
5, 1, 0 + 1/2
|
|
Arindam Khanna answered |
Electronic configuration of Rb = [Kr] 5s–1 Set of quantum numbers, n = 5
ℓ = 0, ∴ s orbital m = 0, s = + 1/2
ℓ = 0, ∴ s orbital m = 0, s = + 1/2
Which of the following is never true for cathode rays ?[1994]- a)They possess kinetic energy
- b)They are electromagnetic waves
- c)They produce heat
- d)They produce mechanical pressure.
Correct answer is option 'B'. Can you explain this answer?
Which of the following is never true for cathode rays ?[1994]
a)
They possess kinetic energy
b)
They are electromagnetic waves
c)
They produce heat
d)
They produce mechanical pressure.
|
Pooja Choudhary answered |
Cathode r ays are never electromagnetic waves.
An ion has 18 electrons in the outermost shell, it is[1990]- a)Cu+
- b)Th4+
- c)Cs+
- d)K+
Correct answer is option 'A'. Can you explain this answer?
An ion has 18 electrons in the outermost shell, it is[1990]
a)
Cu+
b)
Th4+
c)
Cs+
d)
K+
|
Palak Khanna answered |
Cu+ = 29 – 1 = 28 e– thus the electronic confingration of Cu+ is
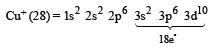
The energy absorbed by each molecule (A2) of a substance is 4.4 × 10–19 J and bond energy per molecule is 4.0 × 10–19 J. The kinetic energy of the molecule per atom will be: [2009]- a)2.2 × 10–19 J
- b)2.0 × 10–19 J
- c)4.0 × 10–20 J
- d)2.0 × 10–20 J
Correct answer is option 'D'. Can you explain this answer?
The energy absorbed by each molecule (A2) of a substance is 4.4 × 10–19 J and bond energy per molecule is 4.0 × 10–19 J. The kinetic energy of the molecule per atom will be: [2009]
a)
2.2 × 10–19 J
b)
2.0 × 10–19 J
c)
4.0 × 10–20 J
d)
2.0 × 10–20 J
|
Aashna Mukherjee answered |
K.E per atom
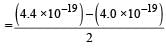
The total number of atomic orbitals in fourth energy level of an atom is : [2011]- a)8
- b)16
- c)32
- d)4
Correct answer is option 'B'. Can you explain this answer?
The total number of atomic orbitals in fourth energy level of an atom is : [2011]
a)
8
b)
16
c)
32
d)
4
|
Dipika Das answered |
Total no. of atomic orbital in a shell = n2.
Given n = 4; Hence number of atomic orbitals in 4th shell will be 16.
Given n = 4; Hence number of atomic orbitals in 4th shell will be 16.
The value of Planck’s constant is 6.63 × 10–34 Js.The speed of light is 3 × 1017 nm s–1.. Which value is closest to the wavelength in nanometer of a quantum of light with frequency of 6 × 1015 s–1? [NEET 2013]- a)25
- b)50
- c)75
- d)10
Correct answer is option 'B'. Can you explain this answer?
The value of Planck’s constant is 6.63 × 10–34 Js.The speed of light is 3 × 1017 nm s–1.. Which value is closest to the wavelength in nanometer of a quantum of light with frequency of 6 × 1015 s–1? [NEET 2013]
a)
25
b)
50
c)
75
d)
10
|
|
Aashna Mukherjee answered |
C = νλ
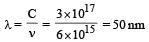
Wh ich of the followin g is not per missible arrangement of electrons in an atom? [2009]- a)n = 5, l = 3, m = 0, s = + 1/2
- b)n = 3, l = 2, m = – 3, s = – 1/2
- c)n = 3, l = 2, m = – 2, s = – 1/2
- d)n = 4, l = 0, m = 0, s = – 1/2
Correct answer is option 'B'. Can you explain this answer?
Wh ich of the followin g is not per missible arrangement of electrons in an atom? [2009]
a)
n = 5, l = 3, m = 0, s = + 1/2
b)
n = 3, l = 2, m = – 3, s = – 1/2
c)
n = 3, l = 2, m = – 2, s = – 1/2
d)
n = 4, l = 0, m = 0, s = – 1/2
|
|
Pranavi Banerjee answered |
Explanation:
Permissible arrangement of electrons in an atom:
- In an atom, the electrons are arranged in different energy levels represented by the principal quantum number (n).
- Each energy level can have sublevels represented by the azimuthal quantum number (l).
- The magnetic quantum number (m) specifies the orientation of the orbital in space.
- The spin quantum number (s) specifies the spin of the electron.
Analysis of the given options:
- Option a: n = 5, l = 3, m = 0, s = +1/2 - This is a permissible arrangement as it follows the rules of quantum numbers.
- Option b: n = 3, l = 2, m = -3, s = -1/2 - This arrangement is not permissible because the magnetic quantum number (m) cannot be greater than the azimuthal quantum number (l) in magnitude.
- Option c: n = 3, l = 2, m = -2, s = -1/2 - This is a permissible arrangement as it follows the rules of quantum numbers.
- Option d: n = 4, l = 0, m = 0, s = -1/2 - This is a permissible arrangement as it follows the rules of quantum numbers.
Therefore, the correct answer is option 'B' because the magnetic quantum number (m) is not valid for the given values of n and l.
Permissible arrangement of electrons in an atom:
- In an atom, the electrons are arranged in different energy levels represented by the principal quantum number (n).
- Each energy level can have sublevels represented by the azimuthal quantum number (l).
- The magnetic quantum number (m) specifies the orientation of the orbital in space.
- The spin quantum number (s) specifies the spin of the electron.
Analysis of the given options:
- Option a: n = 5, l = 3, m = 0, s = +1/2 - This is a permissible arrangement as it follows the rules of quantum numbers.
- Option b: n = 3, l = 2, m = -3, s = -1/2 - This arrangement is not permissible because the magnetic quantum number (m) cannot be greater than the azimuthal quantum number (l) in magnitude.
- Option c: n = 3, l = 2, m = -2, s = -1/2 - This is a permissible arrangement as it follows the rules of quantum numbers.
- Option d: n = 4, l = 0, m = 0, s = -1/2 - This is a permissible arrangement as it follows the rules of quantum numbers.
Therefore, the correct answer is option 'B' because the magnetic quantum number (m) is not valid for the given values of n and l.
The total number of electrons that can be accommodated in all the orbitals having principal quantum number 2 and azimuthal quantum number 1 is [1990]- a)2
- b)4
- c)6
- d)8
Correct answer is option 'C'. Can you explain this answer?
The total number of electrons that can be accommodated in all the orbitals having principal quantum number 2 and azimuthal quantum number 1 is [1990]
a)
2
b)
4
c)
6
d)
8
|
Ayush Sengupta answered |
n = 2, l = 1 means 2 p – orbital. Electrons that can be accommodated = 6 as p sub-shell has 3 orbital and each orbital contains 2 electrons.
The number of spherical nodes in 3p orbitals are [1988]- a)one
- b)three
- c)none
- d)two
Correct answer is option 'A'. Can you explain this answer?
The number of spherical nodes in 3p orbitals are [1988]
a)
one
b)
three
c)
none
d)
two
|
Krish Chakraborty answered |
No. of radial nodes in 3p-orbital = (n – ℓ – 1) [for p ortbital ℓ = 1] = 3 – 1 – 1 = 1
The value of Planck's constant is 6.63 × 10–34 Js.The velocity of light is 3.0 × 108 m s–1. Which value is closest to the wavelength in nanometers of a quantum of light with frequency of 8 × 1015 s–1 ? [2003]
- a)3 × 107
- b)2 × 10–25
- c)5 × 10–18
- d)4 × 101
Correct answer is option 'D'. Can you explain this answer?
The value of Planck's constant is 6.63 × 10–34 Js.The velocity of light is 3.0 × 108 m s–1. Which value is closest to the wavelength in nanometers of a quantum of light with frequency of 8 × 1015 s–1 ? [2003]
a)
3 × 107
b)
2 × 10–25
c)
5 × 10–18
d)
4 × 101
|
Shanaya Rane answered |
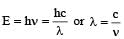
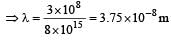
In nanometer λ = 3.75× 10 which is closest to 4 × 101
In the photo-electron emission, the energy of the emitted electron is [1994]- a)greater than the incident photon
- b)same as than of the incident photon
- c)smaller than the incident photon
- d)proportional to th e in ten sity of inciden t photon.
Correct answer is option 'C'. Can you explain this answer?
In the photo-electron emission, the energy of the emitted electron is [1994]
a)
greater than the incident photon
b)
same as than of the incident photon
c)
smaller than the incident photon
d)
proportional to th e in ten sity of inciden t photon.
|
|
Rhea Sarkar answered |
K.E. of emitted electron = hν - hν0 (i.e. smaller than hν ).
In a given atom no two electrons can have the same values for all the four quantum numbers.This is called [1991]- a)Hund’s Rule
- b)Aufbau principle
- c)Uncertainty principle
- d)Pauli’s Exclusion principle.
Correct answer is option 'D'. Can you explain this answer?
In a given atom no two electrons can have the same values for all the four quantum numbers.This is called [1991]
a)
Hund’s Rule
b)
Aufbau principle
c)
Uncertainty principle
d)
Pauli’s Exclusion principle.
|
Siddharth Mehra answered |
's rule
b)Pauli exclusion principle
c)Aufbau principle
d)Heisenberg uncertainty principle
The correct answer is b) Pauli exclusion principle.
b)Pauli exclusion principle
c)Aufbau principle
d)Heisenberg uncertainty principle
The correct answer is b) Pauli exclusion principle.
For which one of the following sets of four quantium numbers, an electron will have the heighst energy? [1994]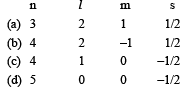
- a)a
- b)b
- c)c
- d)d
Correct answer is option 'B'. Can you explain this answer?
For which one of the following sets of four quantium numbers, an electron will have the heighst energy? [1994]
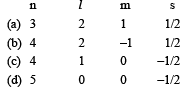
a)
a
b)
b
c)
c
d)
d
|
Mehul Iyer answered |
The sub-shell are 3d, 4d, 4p and 4s, 4d has highest energy as n + ℓ value is maximum for this.
The position of both , an electron and a helium atom is known within 1.0 nm. Further the momentum of the electron is known within 5.0 × 10–26 kg ms–1. The minimum uncertainty in the measurement of the momentum of the helium atom is [1998]- a)50 kg ms–1
- b)80 kg ms–1
- c)8.0 × 10–26 kg ms–1
- d)5.0 × 10–26 kg ms–1
Correct answer is option 'D'. Can you explain this answer?
The position of both , an electron and a helium atom is known within 1.0 nm. Further the momentum of the electron is known within 5.0 × 10–26 kg ms–1. The minimum uncertainty in the measurement of the momentum of the helium atom is [1998]
a)
50 kg ms–1
b)
80 kg ms–1
c)
8.0 × 10–26 kg ms–1
d)
5.0 × 10–26 kg ms–1
|
|
Chirag Mehta answered |
Understanding Uncertainty Principle
The uncertainty principle, formulated by Heisenberg, states that the more precisely the position of a particle is known, the less precisely its momentum can be known, and vice versa. This is mathematically represented as:
Δx * Δp ≥ h / (4π)
Where:
- Δx is the uncertainty in position
- Δp is the uncertainty in momentum
- h is Planck's constant (approximately 6.63 × 10^-34 Js)
Given Information
- The position uncertainty (Δx) for both the electron and the helium atom is 1.0 nm (1.0 × 10^-9 m).
- The momentum uncertainty (Δp) for the electron is given as 5.0 × 10^-26 kg m/s.
Calculating Momentum Uncertainty for Helium Atom
1. Position Uncertainty: For helium, Δx = 1.0 × 10^-9 m.
2. Using the Uncertainty Principle:
To find the momentum uncertainty for helium (Δp_He), we will use the known Δp of the electron as a reference and scale it based on the mass difference.
3. Mass Consideration:
The mass of the helium atom is approximately four times that of an electron.
- Mass of electron (m_e) ≈ 9.11 × 10^-31 kg
- Mass of helium (m_He) ≈ 4 * m_e ≈ 3.64 × 10^-30 kg
4. Scaling Δp:
Since momentum uncertainty scales with mass, the uncertainty in momentum for helium can be approximately the same as that for the electron due to the similar Δx. Thus:
- Δp_He ≈ Δp_electron = 5.0 × 10^-26 kg m/s.
Conclusion
Therefore, the minimum uncertainty in the measurement of the momentum of the helium atom is the same as that of the electron, which is 5.0 × 10^-26 kg m/s. Hence, the correct answer is option 'D'.
The uncertainty principle, formulated by Heisenberg, states that the more precisely the position of a particle is known, the less precisely its momentum can be known, and vice versa. This is mathematically represented as:
Δx * Δp ≥ h / (4π)
Where:
- Δx is the uncertainty in position
- Δp is the uncertainty in momentum
- h is Planck's constant (approximately 6.63 × 10^-34 Js)
Given Information
- The position uncertainty (Δx) for both the electron and the helium atom is 1.0 nm (1.0 × 10^-9 m).
- The momentum uncertainty (Δp) for the electron is given as 5.0 × 10^-26 kg m/s.
Calculating Momentum Uncertainty for Helium Atom
1. Position Uncertainty: For helium, Δx = 1.0 × 10^-9 m.
2. Using the Uncertainty Principle:
To find the momentum uncertainty for helium (Δp_He), we will use the known Δp of the electron as a reference and scale it based on the mass difference.
3. Mass Consideration:
The mass of the helium atom is approximately four times that of an electron.
- Mass of electron (m_e) ≈ 9.11 × 10^-31 kg
- Mass of helium (m_He) ≈ 4 * m_e ≈ 3.64 × 10^-30 kg
4. Scaling Δp:
Since momentum uncertainty scales with mass, the uncertainty in momentum for helium can be approximately the same as that for the electron due to the similar Δx. Thus:
- Δp_He ≈ Δp_electron = 5.0 × 10^-26 kg m/s.
Conclusion
Therefore, the minimum uncertainty in the measurement of the momentum of the helium atom is the same as that of the electron, which is 5.0 × 10^-26 kg m/s. Hence, the correct answer is option 'D'.
If electron has spin quantum number + 1/2 and a magnetic quantum number – 1, it cannot be present in [1994]- a)d-orbital
- b)f-orbital
- c)p-orbital
- d)s-orbital.
Correct answer is option 'D'. Can you explain this answer?
If electron has spin quantum number + 1/2 and a magnetic quantum number – 1, it cannot be present in [1994]
a)
d-orbital
b)
f-orbital
c)
p-orbital
d)
s-orbital.
|
Ashish Roy answered |
The magnetic quantum number of an electron depends on its spin quantum number. For an electron with a spin quantum number of 1/2, the possible magnetic quantum numbers are +1/2 and -1/2. These values represent the two possible orientations of the electron's spin in a magnetic field.
If the energy of a photon is given as : = 3.03 × 10–19 J then, the wavelength (λ) of the photon is :- a)6.56 nm
- b)65.6 nm [2000]
- c)656 nm
- d)0.656 nm
Correct answer is option 'C'. Can you explain this answer?
If the energy of a photon is given as : = 3.03 × 10–19 J then, the wavelength (λ) of the photon is :
a)
6.56 nm
b)
65.6 nm [2000]
c)
656 nm
d)
0.656 nm
|
Shilpa Saha answered |
Understanding Photon Energy and Wavelength
To find the wavelength (λ) of a photon given its energy, we can use the formula:
E = hc / λ
where:
- E is the energy of the photon (in joules)
- h is Planck's constant (6.626 × 10^(-34) J·s)
- c is the speed of light (3.00 × 10^8 m/s)
Steps to Calculate Wavelength
1. Rearranging the Formula
We can rearrange the formula to solve for wavelength:
λ = hc / E
2. Substituting Values
Given E = 3.03 × 10^(-19) J, we substitute the known values into the formula:
λ = (6.626 × 10^(-34) J·s * 3.00 × 10^8 m/s) / (3.03 × 10^(-19) J)
3. Calculating the Wavelength
Performing the calculation:
λ = (1.9878 × 10^(-25) J·m) / (3.03 × 10^(-19) J)
λ ≈ 6.56 × 10^(-7) m or 656 nm
Conclusion
The calculated wavelength of the photon is approximately 656 nm. This corresponds to the visible light spectrum, specifically in the red region. Therefore, the correct answer is option 'C' - 656 nm.
To find the wavelength (λ) of a photon given its energy, we can use the formula:
E = hc / λ
where:
- E is the energy of the photon (in joules)
- h is Planck's constant (6.626 × 10^(-34) J·s)
- c is the speed of light (3.00 × 10^8 m/s)
Steps to Calculate Wavelength
1. Rearranging the Formula
We can rearrange the formula to solve for wavelength:
λ = hc / E
2. Substituting Values
Given E = 3.03 × 10^(-19) J, we substitute the known values into the formula:
λ = (6.626 × 10^(-34) J·s * 3.00 × 10^8 m/s) / (3.03 × 10^(-19) J)
3. Calculating the Wavelength
Performing the calculation:
λ = (1.9878 × 10^(-25) J·m) / (3.03 × 10^(-19) J)
λ ≈ 6.56 × 10^(-7) m or 656 nm
Conclusion
The calculated wavelength of the photon is approximately 656 nm. This corresponds to the visible light spectrum, specifically in the red region. Therefore, the correct answer is option 'C' - 656 nm.
According to the Bohr Theory, which of the following transitions in the hydrogen atom will give rise to the least energetic photon ? [2011 M]- a)n = 6 to n = 1
- b)n = 5 to n = 4
- c)n = 6 to n = 5
- d)n = 5 to n = 3
Correct answer is option 'C'. Can you explain this answer?
According to the Bohr Theory, which of the following transitions in the hydrogen atom will give rise to the least energetic photon ? [2011 M]
a)
n = 6 to n = 1
b)
n = 5 to n = 4
c)
n = 6 to n = 5
d)
n = 5 to n = 3
|
|
Harshitha Dey answered |
Energy of photon obtained from the transition n = 6 to n = 5 will have least energy.
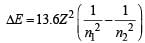
The radius of hydrogen atom in the ground state is 0.53 Å. The radius of Li2+ ion (atomic number = 3) in a similar state is [1995]- a)0.17 Å
- b)0.265 Å
- c)0.53 Å
- d)1.06 Å
Correct answer is option 'A'. Can you explain this answer?
The radius of hydrogen atom in the ground state is 0.53 Å. The radius of Li2+ ion (atomic number = 3) in a similar state is [1995]
a)
0.17 Å
b)
0.265 Å
c)
0.53 Å
d)
1.06 Å
|
Mahesh Saini answered |
State of hydrogen atom (n) = 1 (due to ground state) Radius of hydrogen atom (r) = 0.53 Å.
Atomic number of Li (Z) = 3.
Radius of Li2+ ion
Atomic number of Li (Z) = 3.
Radius of Li2+ ion
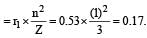
The Bohr orbit radius for the hydrogen atom (n = 1) is approximately 0.530 Å. The radius for the first excited state (n = 2) orbit is (in Å) [1998]- a)0.13
- b)1.06
- c)4.77
- d)2.12
Correct answer is option 'D'. Can you explain this answer?
The Bohr orbit radius for the hydrogen atom (n = 1) is approximately 0.530 Å. The radius for the first excited state (n = 2) orbit is (in Å) [1998]
a)
0.13
b)
1.06
c)
4.77
d)
2.12
|
|
Shounak Nair answered |
Given : Radius of hydrogen atom = 0.530 Å,
Number of excited state (n) = 2 and atomic number of hydrogen atom (Z) = 1. We know that the Bohr radius.
Number of excited state (n) = 2 and atomic number of hydrogen atom (Z) = 1. We know that the Bohr radius.
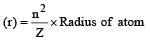
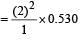
= 4 x 0.530 = 2.12 Å
Chapter doubts & questions for Structure of Atom - Chemistry 31 Years NEET Chapterwise Solved Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Structure of Atom - Chemistry 31 Years NEET Chapterwise Solved Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Chemistry 31 Years NEET Chapterwise Solved Papers
23 docs|37 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily